基于行为向量的在线事件流预测
卢 可,方贤文,2+,方 娜
(1.安徽理工大学 数学与大数据学院,安徽 淮南 232001;2.同济大学 嵌入式系统与服务计算教育部重点实验室,上海 201804)
0 引言
业务流程监控在运行时分析系统执行信息,以了解系统的性能和与目标的偏差。预测能够提前感知异常情况,在业务流程监控中发挥着重要的作用[1]。常见的预测目标包括预测案例完成之前的剩余时间[2-4]、下一个活动[5-7]、下一个时间戳[8-9]、所使用的资源[10]等。其中,预测下一个活动能够使业务流程的相关人员预先对系统中的风险采取应对措施,预防系统出现问题[11]。为了能对逐年骤增的业务流程及时做出反应,近年很多学者开始关注在线过程分析[12],而正在运行的实例信息通常以事件流的形式记录,因此研究基于在线事件流愈发重要。
早期研究通常关注存储于数据库的离线数据[13],通过隐马尔科夫模型等统计方法分析信息系统生成的日志信息,获得对企业面临的相关问题的深入思考[14]。还有一些研究采用推荐系统中的方法分析日志,以推荐下一个活动的形式进行预测分析[15]。
近些年,随着计算机硬件和人工智能的发展,一些研究受到自然语言处理(Natural Language Processing, NLP)的启发,将事件日志视为文本,引入深度学习的思想,将预测下一个事件转为预测句子中下一个单词的问题来处理[16]。在此背景下,循环神经网络(Recurrent Neural Network, RNN)[17]、长—短期记忆网络(Long Short Term Memory, LSTM)[9,18]、卷积神经网络(Convolutional Neural Networks, CNN)[11,19]、堆叠式自动编码器[20]等各种先进的神经网络被应用于预测下一个事件场景。EVERMANN等[17]描述了具有递归神经网络的深度学习在预测下一个过程事件上的初步应用;CAMARGO等[9]提出一种采用LSTM架构训练递归神经网络的方法,以预测下一个事件的剩余序列、运行周期时间及相关资源;LIN等[18]采用LSTM网络对事件信息及其属性分别编码,然后将其组合在一起作为给定序列历史信息的隐藏表示,再用另一个LSTM层作为解码器,同时对下一个事件及其属性进行预测。受到前期深度学习算法在预测性过程挖掘领域的启发,AL-JEBRNI等[11]采用五层一维卷积神经网络(one-Dimensional Convolution Neural Network, 1D CNN)预测下一个过程事件,并在所提供的数据集上取得当时同领域最佳的表现;PASQUADIBISCEGLIE等[19]同样采用CNN将业务流程历史事件日志中包含的时间数据转换为空间数据,然后用空间数据训练CNN,以预测下一个活动;MEHDIYEV等[20]则采用一种多阶段的深度学习算法,包括无监督的预训练组件与堆叠的自动编码器和有监督的微调组件,并在各种业务流程日志数据集上得到了较好的结果。
虽然深度学习领域的方法均已成功用于真实案例,但是仍然存在一些缺陷。目前关于预测下一个事件的方法以事件流为研究起点,采用One-Hot编码[2,7,10,21]或者基于事件的频率[19]表示事件流。One-Hot编码具有以下特点:①假设对象之间相互独立;②不考虑对象之间的顺序。
然而事件流之间不仅相互影响,还有特定的行为关系,因此采用One-Hot编码会导致研究过程中缺少对事件流行为的分析。因此,本文提出基于行为编码的预测方法,主要贡献如下:
(1)定义了基于实时数据的事件流行为轮廓。通过细化事件流之间的行为关系,捕获活动之间的顺序、循环、并发及排他关系。
(2)提出一种新的事件编码方式——行为编码,对活动进行编码,从而衡量活动之间的行为距离、内在联系和活动顺序。
(3)采用协同过滤的思想对当前事件流进行推荐,从而预测下一个可能发生的事件流。
1 基本概念
本章介绍了本文所需的背景知识,包括活动、迹、事件日志(如表1)、事件流和传统的模型行为轮廓。
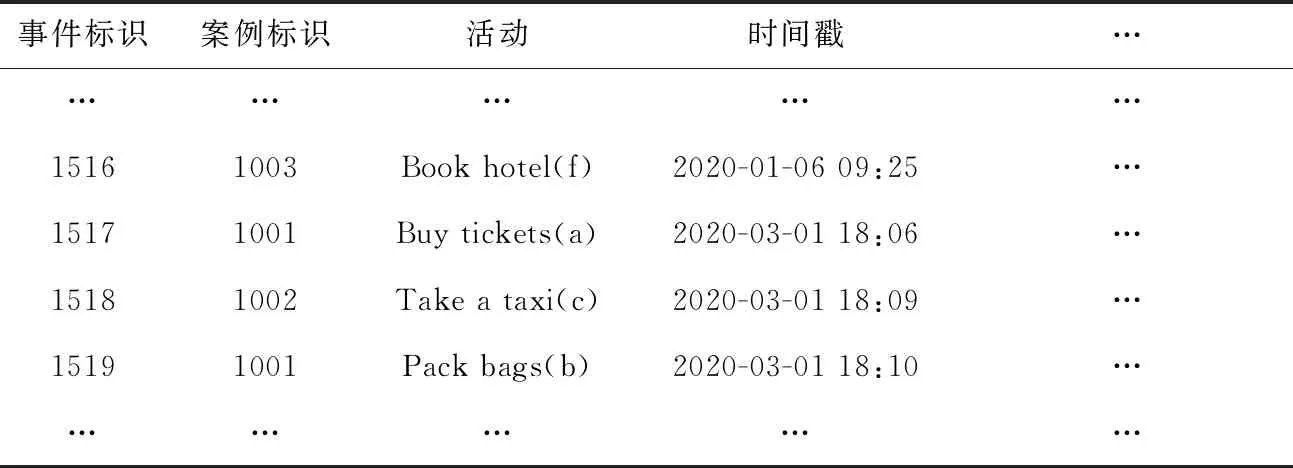
表1 事件日志片段
1.1 日志和事件流

事件是活动的一次执行,可以由各种属性表征。例如,事件可以具有时间戳、与活动相对应的名称、特定的执行人员和执行的相关成本等属性。事件日志由多组事件序列构成,其与事件流的区别在于,事件日志是存储于数据库或本地文档的有限、离线数据,事件流是系统运行时的无限、实时数据。
定义2事件流[23]。A为一组活动集,C为所有可能的案例标识符的集合。事件流S=(c,a)为C×A上的序列,即S∈(C×A)*,其中c∈C,a∈A。
Si=(c,a)表示i时刻,案例标识符为c,发生了活动a。两个事件流之间的距离记为D(Si,Sj)。Si的下一个事件流Sj需同时满足两个条件:①与Si具有相同的案例标识符;②与Si距离最小。
1.2 模型的行为轮廓
为了捕获过程模型的基本行为约束,本节引入模型行为轮廓的概念(简称行为轮廓)。
定义3行为轮廓[24]。假设(N,M0)为一个网,对于任意变迁对(t1,t2)∈(T×T):
(1)若t1≻t2且t2t1,则t1和t2为严格序关系,记作t1→t2。
(2)若t1t2且t2≻t1,则t1和t2为严格逆序关系,记作t1←-1t2。
(3)若t1t2且t2t1,则t1和t2为排他关系,记作t1+t2。
(4)若t1≻t2且t2≻t1,则t1和t2为交叉序关系,记作t1||t2。
将所有关系的集合称为网系统的行为轮廓,记作BP={→,←-1,+,||}。
1.3 协同过滤
作为推荐系统中的重要技术,协同过滤[25]广泛应用于电子商务,根据用户或项目之间的关系,其能够从候选集中推荐出最相似的选择。本文将预测系统运行的事件流问题预测视为一种推荐问题,采用推荐系统领域的方法分析系统的运行情况,实时预测事件流的发生。传统的协同过滤算法分为基于用户的协同过滤、基于项目的协同过滤、基于模型的协同过滤3种类型,其中前两种属于基于记忆的协同过滤算法,因此具有相似的分析步骤[26]:
(1)计算用户或项目之间的相似度 通过分析数据之间的关系比较数据中间的相似性。传统的相似度度量方法有皮尔逊相关系数法、向量余弦法等[27]。
(2)寻找相似近邻 经过(1)计算后,需要选择所需的相似的数据。寻找相似近邻的方法主要有使用设定阈值和k近邻搜索算法。
(3)TopN推荐[28]协同过滤算法根据近邻信息为用户返回候选的推荐列表。本文采用协同过滤的基本思想,将其应用到实时预测的事件流情景中。
2 基于事件流行为向量的预测
当前研究工作已经对各种预测方法进行了探索,如基于Markov等统计模型的预测方法、基于自动机的预测方法和基于Petri网的预测方法等(关于这几类方法的对比可参阅文献[6]),这些方法在分析事件日志或事件流时,有些只考虑活动与前驱和后继的关系,有些只考虑活动本身的状态,有些甚至没有体现活动之间的关系。为了在预测分析过程中考虑事件流以及所有事件流之间的行为关系,需要一种新的事件流编码方式将事件流输入到算法中。因此,本章提出一种协同过滤算法,基于事件流的行为向量实时预测系统中即将发生的下一个事件流。
2.1 定义事件流行为轮廓
传统的行为轮廓旨在分析模型中活动之间的序列关系,捕获过程模型中存在的基本行为约束[24]。本文需要对事件流进行分析,而传统的行为轮廓无法直接满足需求,因此本节基于传统的行为轮廓重新定义一组行为轮廓关系概念来描述在线事件流之间的关系。
对于事件流S,寻找与其具有相同案例标识符的事件流S′,基于这两个事件流,给出事件流严格序的定义。为了便于体现事件发生的顺序,在事件流的定义中考虑事件的发生时间t。


图1所示为严格序的简单示例,其中S1=(1001,a)和S3=(1001,b)是一对严格序关系的事件流。因为S1和S3的案例标识符均为1001,S2=(1002,e)的案例标识符为1002,不满足定义的第一个条件,而S6=(1001,c)的案例标识符虽然也是1001,但是D(S1,S6)=5>D(S1,S3)=2,所以S6并不是与S1距离最近的下一个事件流。

严格序反映了事件之间的顺序关系,其前件事件流的发生时间在前,后件事件流的发生时间在后,后面发生的事件总是在前面发生的事件之后,因此容易推导出严格序具有传递性,将此传递性形式化为性质1:

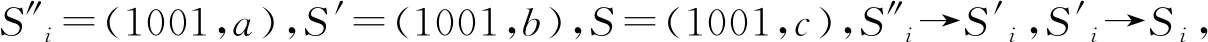
定义5事件流间接严格序。事件流间接严格序简称为间接严格序,记为,事件流和Si之间的间接严格序表示为
基于模型结构的行为轮廓可以快速获取行为之间的各种关系,然而在源源不断的实时数据流中,能直接获取的只有前后密切相关的严格序。因此,欲分析事件流中的所有事件,只关注某一时刻的运行状态远远不够。这里将观察的范围扩大,使用输入流的滑动窗口[29]对接收的数据进行分析。
如果对于任意c∈C,滑动窗口w中的事件流Si和Sj都不存在i和j,使得Si→Sj或者Sj→Si,则Si和Sj为事件流排他序。如图2所示,Si=(1001,b)和Sj=(1002,c)在窗口w中为排他序。

定义6事件流排他序。事件流排他序简称为排他序,记为+,Si和Sj之间的排他序表示为Si+Sj,if ∀i,j∈[0,∞],c∈C⟹SiSj∨SjSi。
从传统行为轮廓的定义可知,出现交叉序的情况分为两种:①并发结构导致的事件发生顺序不确定,而且事件不处于任何一个循环结构中;②由于循环结构导致一组事件重复发生,从而使同一活动在执行时呈现交叉序。这两种情况增大了分析模型的难度,因此将交叉序细化,分为并发交叉序和循环交叉序两种情况分别讨论。
如果在窗口w中,对于Si和Sj既有Si→Sj,又有Sj→Si,则Si和Sj为交叉序。
定义7事件流并发交叉序。事件流并发交叉序简称为交叉序,记为||,Si和Sj之间的交叉序表示为Si||Sj,if ∀i,j∈[0,∞],∃c1∈C⟹Si→Sj∧∃c2∈C⟹Sj→Si。
如果在窗口w中一组事件流重复出现,则这组事件流中的每个事件与其自身为循环交叉序(如图3),循环体的不同事件之间是严格序。

定义8事件流循环交叉序。事件流循环交叉序简称为循环交叉序,Si和Sj之间的循环交叉序表示为Si||○Sj,if …SiSi+1Si+2S…Sj…,∃i,j∈[0,∞]⟹Si=Sj。
定义9事件流循环内严格序。简称为循环内严格序(如图4),Si和Sj之间的循环内严格序表示为Si○→Sj,如果存在一个案例c,使Si和Sj处于一个循环序列中,且Si→Sj。

以上定义的6种事件流之间的关系形成了事件流的行为轮廓,而事件发生的频率在一定程度上能够体现其在系统中的重要性,因此将频率作为事件流行为轮廓的一部分。
定义10事件流行为轮廓EBP。EBPR={…,(Si,Sj)N,…},i,j∈(1,∞),其中R={→,,||,||○,○→,+}为行为关系,N为R在窗口w内发生的次数,记作∏(SiRSj)=N。
2.2 在线识别事件流行为轮廓
本节通过在线事件流行为轮廓,从正在运行的系统中学习事件流之间的行为关系。因为事件流是活动在某一时刻的运行状态,数据项的顺序已经由每个项到达的时间戳决定[25],所以在特定时刻只能观察到某个事件及其前一个事件。而事件流行为轮廓的后3种关系均建立在严格序的基础上,因此首先需要从事件流中获取严格序关系。
首先假设事件流为单线程,这样系统中每次只有一个案例c1在发生,当c1结束后,c2才可以发生。采用一个集合EBP→存储获取的所有严格序。在时刻i,观察到事件流Si及其上一个事件Si-1,根据定义2判断Si-1和Si之间的关系为严格序,即Si-1→Si,将其加入集合EBP→,此时EBP→={(Si-1,Si)}。同样,在时刻j对其进行同样操作,可得Sj-1→Sj。以此类推,每个新到达的事件流均被立即处理。如果该严格序是第一次出现,即Si-1≠Sj-1或Si≠Sj,则直接加入集合,此时EBP→={(Si-1,Si),(Sj-1,Sj)};如果已经在集合中出现了至少一次,如Si-1=Sj-1且Si=Sj,则更新该项的次数,记为EBP→={(Si-1,Si)2}。
上述分析只适用于理想情况,即连续的事件流都属于同一个案例c,且事件发生时必须是连续、不可中断的,然而这种理想状况在实际中出现的概率非常低,而且因为硬件的快速发展,绝大多数系统都支持多线程同时进行,只着眼于某一时刻无法洞悉整个系统的结构,所以引入滑动窗口来扩大事件流的检测视图,构造滑动窗口中所有活动之间的行为关系矩阵。
滑动窗口分为基于时间定义的滑窗和基于元组个数定义的计数滑窗两类,本文基于滑动窗口观察运行的事件流,将事件流按照发生的时间戳重新定义单位时间,只考虑事件流的到达顺序而不关注具体的时间点,即采用基于元组个数定义的滑动窗口。
为了同时分析滑动窗口中的多个案例,需要设置一个缓存机制。首先将滑动窗口内各个案例的第1个事件Si=(ci,xi),Sj=(cj,xj),Sk=(ck,xk)等保存到缓存机制中,当下一时刻匹配到拥有相同案例标识符的第2个事件时,如出现Si+1=(ci,xi+1),将该案例的第1个Si=(ci,xi)从缓存机制中取出,采用本节开始的方法对Si和Si+1进行分析。重复以上步骤,直到事件流结束,可以获得一个当前滑动窗口范围内观测到的所有事件流的一个完整严格序集EBP→={(S1,S2)m,…,(Si,Sj)n,…}。
由于滑动窗口视图扩大了分析的范围,此时可以观察到事件流中包含的循环结构。对于其中的循环结构,通过循环交叉序的定义可以识别出符合循环交叉序的事件流,将其加入循环交叉序集EBP||○。若Si=(ci,xi)||○Si=(ci,xi),则Si中的xi为循环体的起始事件,将其作为循环的开始标志。对循环体只分析一次,以避免重复分析,循环体内部的严格序加入循环严格序集EBP||→中。
随后通过严格序集,根据定义推导其他行为关系。如果不包含循环结构,而且在严格序集EBP→中,既有(Si,Sj)n也有(Sj,Si)m,则Si和Sj为并发交叉序关系,将其加入并发交叉序集EBP||中。为了全面探索活动之间的行为关系,用行为关系矩阵表示已经获得的行为关系。
定义11行为关系矩阵
EBP→∪EBP∪EBP○→∪EBP||∪EBP||○
∪EBP+,Rij∈{→,,○→,||,||○,+}。
行为关系矩阵的行和列分别表示事件流中的活动集,矩阵中的元素表示活动对之间的行为关系及发生频率。将严格序集和循环交叉序的元素存储在行为关系矩阵的对应位置,很容易推导出间接严格序,将其存入间接严格序集EBP中。此时矩阵中仍然存在空值,表示对应的两个活动x,y之间没有前面所述的4种行为关系,即x,y为排他序,将对应事件存入排他序集EBP+中。最后将4个集合中的元素按照对应关系存入行为关系矩阵,将推导事件流之间行为关系的步骤形式化为算法1。
算法1推导事件流行为关系。
输入:事件流S。
输出:事件流行为矩阵M。
1 Initialization Slide Window w,Event Stream Behavioural MatrixM, EBP→,EBP,EBP‖,EBP,EBP,EBP+;
2 for S in w do
3 if (Si,Sj) in EBP→then
4 ∏(Si,Sj)=N+1
5 else
6 EBP→←(Si,Sj)
7 end
8 if Sj=Skin Sito Si+wthen
9 EBP←(Sj,Sj);
10 EBP←other event stream between Siand Si+w
11 end
12 end
13 for i,j inMdo
14 if Mijis null then
15 if (Si,Sj)nand (Sj,Si)min EBP→then EBP‖→←(Si,Sj)n,(Sj,Si)m;
16 if (Sx,Sx+1),…,(Sx+y-1,Sx+y) in EBP→then EBP←(Sx,Sx+y);
17 else EBP+←(Si,Sj);
18 end
19 end
20M←EBP→∪EBP∪EBP‖∪EBP∪EBP∪EBP+
输出:M
算法1第1~11行通过缓存事件流直接获取一部分事件流行为轮廓关系。其中第3~7行分析一对事件流的严格序关系,如果该关系已经存在于事件流行为矩阵M中,则计数加1,否则将其存入事件流严格序集EBP→中。如果该关系的逆已经存在于M中,则将其关系替换为循环交叉序集EBP||○,并将该关系及其逆序从严格序集中删除。
当对事件流的分析结束时,再基于行为关系矩阵M推导其他行为关系(第12~19行),关于推导循环内严格序、间接严格序和排他序的关系的具体步骤在上文已经给出。第20行获得一个关于事件流中所有活动之间的行为轮廓关系矩阵。
2.3 预测下一个事件
本节以协同过滤算法为基础,对其每一步进行调整以适应事件流场景。首先将事件流序列与事件流之间的行为特征结合,构造一个既能体现行为关系,又能用于协同过滤的事件流向量,然后将其应用于系统的事件流分析,对每个运行中的事件流进行实时预测。
2.3.1 构造行为向量
在描述算法之前,先定义一些新概念。为了便于计算事件流之间的相似度,即具有相同案例标识符的事件构成的序列,需要将向量作为输入。首先定义一个映射函数,将行为轮廓矩阵中的关系映射成为特定的数值。
定义12行为轮廓映射函数。使用行为轮廓映射函数F(R)=N,N∈[-3,3],将行为轮廓矩阵转换为一个整数型行为关系矩阵M′,其每个元素均为特定范围间的整数。
通过定义12将事件流对应的符号转变为数值型数据,这样矩阵中的每一行就可以转变为一个数值型的行向量,将该行向量称为事件流向量。
定义13事件流编码
vi=[F(Ri1),F(Ri2),…,F(Rin)]=Mi,
n=count(Sd)。
式中:vi为第i个事件流的向量形式,n为不相同的事件流Sd的总数。事件流序列是由拥有相同案例标识符的事件流构成的序列。因此,将事件流序列向量表示为事件流向量的连接。
定义14事件流序列编码
V=[…vi·vj…]=[…F(Ri1),F(Ri2),…,
F(Rin),…,F(Rj1),F(Rj2),…,F(Rjn),…]。
2.3.2 预测事件流
事件流的向量表达形式不仅可以用来反映事件流之间的顺序、循环等结构的相似性,还可以量化事件流在空间上的相似性。
定义15相似度
将预测事件流的步骤形式化为算法2,算法思想是基于已经发生的m个事件流,预测第(m+1)个事件流。
算法2预测下一个事件流。
输入:事件流关系矩阵M。
输出:预测结果cond。
1 Initialization Event stream vertor V, similarity event stream squences matrix SimMatrix, Next event stream matrix Vnext;
2 begin
3 v['end']=|Set(events)|
4 M′=F(M)
5 for event,index in Set(events) do
6 v[event]=M′[index]
7 end
8 while event do
//kenel of algorithm
9 V=V.conc(v[event])
10 Vtemp=V.pad(v['end'])
11 foreach event′ in Set(events) do
12 add V.conc(v[event′]) to Vnext
13 end
14 SimMatrix=Sim(Vtemp,Vnext)
15 cond=KNN(SimMatrix,k)
16 end
17 end
构造的事件流序列向量长度为m×|Set(events)|,候选集的长度为(m+1)×|Set(events)|,需要将向量扩充至相同长度。因此,算法2第3行先初始化一个空事件流向量,用于补齐事件流向量;第4行将行为轮廓矩阵中的符号转换为数值型数据,得到对应的整数型关系矩阵;第5~7行将矩阵的每一行赋值给每个事件流,即用事件流行为轮廓定义事件流编码。
算法2第8~17行分析运行中的事件流,每个事件流发生时(第8行),将其转换为对应的事件流编码(第9行)。此时的事件流序列中包含m个事件流,将其扩充到m+1个事件流的长度(第10行)。将候选事件流序列集用Vnext表示,在第11~13行将所有长度为m+1的事件流列入候选集,然后通过Sim函数计算当前事件流序列与候选事件流序列之间的相似度(第14行)。最后,采用k近邻搜索算法得到最终预测结果(第15行)。
3 评估
本文基于Python实现了第2章所提算法。使用开源的过程挖掘项目pm4py[30]将XES[31]格式的日志转换为由事件流构成的CSV格式,然后将其以数据流的形式传入算法中模拟系统实时运行的状态。
3.1 推导行为关系
为便于掌握算法的运行特点,首先采用结构较简单的合成数据测试,然后用真实数据验证结果。
3.1.1 合成数据
首先使用合成事件日志“Artificial-Loan Process-Partial”作为测试数据。为了直观查看日志的流程结构,采用IM(inductive miner)挖掘算法[32]对该日志(包括98个案例、7个活动、372个事件)进行分析,得到一个Petri网形式的过程模型(如图5),然后将事件日志转换为事件流数据。为了确定滑动窗口的视图尺寸,需要了解案例之间的时间跨度(具有相同案例的各个事件流与其第1个事件流之间的距离),图6所示的抖动图(可以将相同位置的点上下分散显示)反映了转储后案例之间的跨度,可见案例之间的距离集中在0~43之间,因此将缓存大小设置为45,舍弃时间跨度过大的案例,获取事件流之间的行为关系。


算法1挖掘合成日志的结果如表2所示。对照图5所示的模型结构可见,事件流之间的各种关系均已正确地呈现在表2中。

表2 合成日志中各个事件之间的行为关系
3.1.2 真实数据
本节采用荷兰金融机构的贷款申请过程相关的日志“BPI Challenge 2017-Offer log”(简称BPI 2017,https://data.4tu.nl/articles/dataset/BPI_Challenge_2017_-_Offer_log/12705737)进行分析。数据包括2016年通过在线系统提交的所有申请及其后续事件,直到2017年2月1日15:11,共计193 849个事件,42 994个案例,8个活动。由于事件发生的时间跨度较大,采用密度图观察时间间隔情况。如图7所示,时间跨度集中在20 000个单位时间内,舍弃该范围之外的数据。
图8所示为采用IM算法从真实日志中挖掘的过程模型,表3所示为采用算法1从事件流中捕获的事件流之间的行为关系矩阵,表4所示为活动名及其缩写。对比之后发现,该日志虽然数量比较庞大,但是事件流之间的行为关系并不复杂,模型与行为关系之间差异较小。



表3 日志BPI2017中活动间的行为关系

表4 日志BPI2017中的活动名及其缩写
3.2 度量行为距离
因为合成日志的行为关系比较简单,所以本节只分析真实日志BPI2017对应的事件流在行为轮廓矩阵与One-Hot编码下的行为距离。
首先比较两种编码下的数值分布。为便于观察,将日志中的活动对应的行为向量编码和One-Hot编码绘制成热图(如图9和图10),x轴和y轴分别为活动的名称和编码。如图9所示,行为向量编码中的数值分布范围较大,活动之间差异明显,更具标识度。在图10所示的One-Hot编码中,数值比较稀疏,只有对角线上的数值为1,其他数值均为0。


采用常用的余弦相似度和Hamming相似度比较每两个活动之间的相似性,如图11和图12所示。相似度与两种编码的数值规律相似,行为向量编码下的活动之间的相似度差异较明显,能够更好地区别不同活动的关系。而One-Hot编码下只有对角线上的活动之间存在关系,其余活动之间无论是顺序、循环序,还是交叉序,都具有相同的相似性,与实际情况不符。
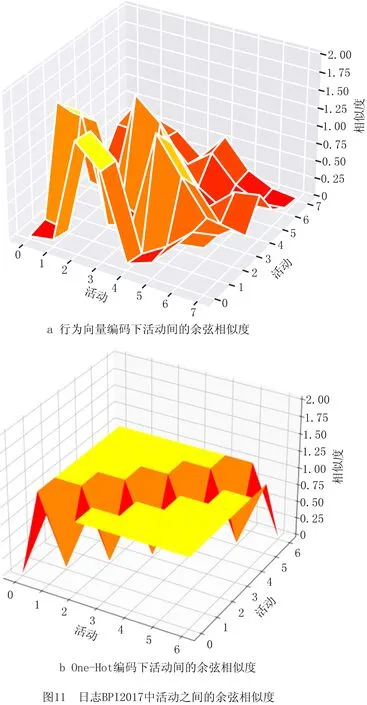

3.3 预测下一个事件流
本节比较使用行为编码和One-Hot编码对预测结果的影响。将事件流序列视为协同过滤中的项目,首先截取部分时间段内的事件流序列进行训练,然后用k近邻搜索算法从候选集中以最佳推荐的形式获得预测值。本文基于scikit-learn(Python实现的机器学习库)进行预测分析,并采用以下度量标准:
(1)预测分数 返回给定测试数据和标签上的平均准确度,预测分数越高,预测效果越好。
(2)Hamming损失 反映预测值和实际值差异程度,数值越小,预测结果越精确。
首先用合成日志进行测试。分别对事件流序列使用以下方式进行处理:①用行为向量编码;②用行为向量编码,同时将数据归一化(sta_enc);③用One-Hot编码(onehot)。
分别选择k(k∈[1,8])个最近邻进行预测,结果如图13所示。随着k的增长,两种编码下的预测结果趋于相同值。这是由于KNN预测模型基于k个临近点的投票机制进行选择,而近邻数达到一定值后,投票的影响超过了编码本身的影响。总体上基于①的预测结果最好,②次之,③的结果总体低于①和②,表明结合了事件之间的联系后,采用行为向量编码具有优势。

用网络4个真实的公共日志“BPI Challenge 2017-Offer log”“Receipt”“Roadtraffic100traces”“Reviewing”(https://github.com/pm4py/pm4py-core/tree/release/tests/input_data)继续验证,结果如表5所示,说明相比One-Hot编码,行为向量编码能在一定程度上提升预测结果。

表5 使用事件流编码对真实日志中事件流预测的结果
4 结束语
本文关注事件流之间的行为关系,提出一种新的事件流编码形式来预测下一个事件流,通过使用少量缓存空间,能够捕获事件流之间的各种行为关系。为了捕获事件流活动之间的关联性,定义了事件流行为轮廓矩阵,在此基础上构建了行为向量编码。相比已有工作中的One-Hot编码,行为向量编码不仅将日志数据转换为深度学习方法的输入,还包含有事件流之间的行为关系。另外,调整后的协同过滤推荐算法能够根据事件流之间的行为相似性更好地进行预测。实验通过合成日志和真实日志证明了本文所提行为向量的优势,以及对协同过滤算法预测结果的提升效果。
本文算法仅考虑了事件流中的行为信息,并未考虑事件流的其他属性,如所用的资源、事件的角色等,未来将根据属性信息细化推荐结果,从而提高预测能力。另外,对于文中的部分参数设置,将采用有监督的机器学习方法进行优化。

