基于改进雷达图综合指标的渠道系统PI控制参数优化

李枭华，管光华

（武汉大学水资源与水电工程科学国家重点实验室，武汉 430072）

0 引言

随着水资源稀缺与供需矛盾的日益明显，节约水资源、提高水资源的利用率已成为实现水资源可持续利用的关键。中国是农业大国，2020 年全国农业用水占用水总量的62.1%，灌溉水有效利用系数为0.565[1]，湖北省某灌区渠系水利用系数为0.713[2]，均有较大提升空间。因此，灌区自动化建设亟待发展，以期提高灌区的用水效率、降低运行成本。

明渠系统作为灌溉输配水的主要手段，其自动化是灌区管理信息化和自动化的重要标志。渠系自动控制目标是为灌区用户提供更加足量及时、安全可靠的供水服务[3]，其核心是控制算法，即从输入信息（水位、流量）到输出的控制动作（闸门开度），以维持相应的控制目的（如下游常水位）的计算逻辑和方法。国内外渠道控制算法可主要分为3类：以传递函数为基础的经典控制算法，以PID类反馈控制算法为代表成果，如P、PI、PID、PIF 等算法；以状态空间为基础的现代控制算法，以LQR、MPC 为代表；以人的思维方式为基础研究复杂系统控制的智能控制算法，如鲁棒控制、自适应算法和神经网络等[4]。由于现代控制算法和智能控制算法尚处于试验和研究阶段，在实际工程中，原理简单、鲁棒性强的PID类经典控制算法应用较为常见，尤其是分布式比例积分(PI)类反馈控制算法研究最为广泛[5-9]。近年来的研究趋势是用智能方法结合经典的PID类经典算法，以获得更良好、更全面的控制性能。韩延成等[10]推导了RBF人工神经网络整定PID输水控制算法，张雨萌等[11]采用粒子群算法进行高效PI 控制参数寻优，叶雯雯[12]采用自适应PI 控制，针对多种优化目标进行分析、比选，比常规PI算法的闸门超调量降低了9%～21%。

渠道系统PI 控制的首要难点是确定控制参数，需要给定一个评价控制性能优劣的量化指标，按照该指标最大化或最小化进行优化求解。目前在渠道控制性能指标领域相关研究较少。美国土木工程师协会（ASCE）渠道控制算法工作组于1998 年提出了一系列基本控制性能指标[13]，对渠系控制性能进行优劣衡量。但该系列指标均只针对水位、流量或闸门的其中一项。而实际工程中仅仅追求单项性能最优，往往会导致其他方面性能的大幅恶化。管光华等[14]对现有性能指标进行去量纲处理，提出了综合指标GI，并以GI 为优化准则整定了PI 控制参数，并与单一指标作为优化准则的结果进行了对比，结果显示追求单一指标的最优难以取得满意结果。

为兼顾控制系统的多方面性能，实现安全可靠、性能均衡的控制目的，本文从输配水渠道系统综合性能评价的问题出发，选取了水位、流量、闸门开度和稳定过渡时间等多个优化目标，提出了基于改进雷达图的综合指标实现多目标综合评价，并以漳河灌区第四干渠为例，验证了该综合指标作为PI控制参数优化目标的有效性。

1 材料与方法

1.1 PI控制算法

PID 算法，即比例积分微分算法，是工业控制中常见的反馈控制算法。在渠道控制算法中，PID 控制算法因简单有效而应用最广。PID 控制算法包括3 个反馈环节，分别是比例环节，积分环节和微分环节，分别对应比例参数Kp，积分参数Ki和微分参数Kd。其中，微分环节对干扰较为敏感，容易造成超调过大、系统失稳的问题，因而在许多工业控制算法中，常使用没有引入微分环节的PI控制器[9]。在本文中的反馈算法逻辑为：将传感器检测得到的水位y(t)反馈到控制中心，该水位和预先设定的目标水位ytarget做比较，其差值为水位误差e(t)，其作为PI 算法的输入量，进行比例、积分两个环节的线性累加计算，得到输出量为流量u(t)，原理见下式：

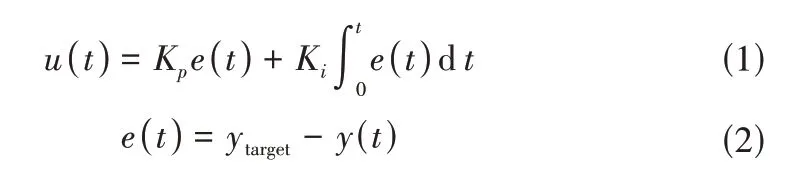
式中：t为运行时间或仿真时间，min。

将上式进行离散处理可得位置式PI控制的离散表达式：

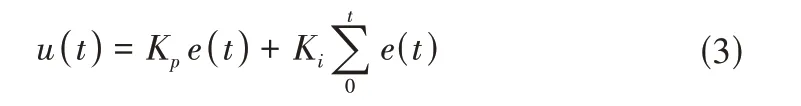
考虑到渠道系统的水动力过程非线性强，复杂性高的特点，对式（3）在时间步上进行作差，得到增量式PI 控制表达式：

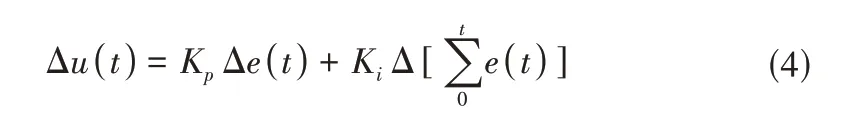
即：

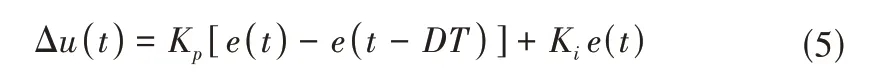
式中：DT为实际采样步长或仿真步长，min。

增量式PI 控制的优点为运算工作量小，手动∕自动切换冲击小，误动作影响小[15]。这些优点更加契合输配水渠道系统的控制要求。

1.2 渠道系统控制结构

由于渠道水波传递的滞后性，不能只依靠反馈控制来进行水位的调节，否则容易出现水位变化超限甚至失稳。在取水流量已知的情况下，通常利用取水流量计划的信息，在取水动作发生的同时，更新目标流量，计算实时的流量校正量，从而使过闸流量向目标流量靠拢，称此步骤为前馈校正，其前馈校正流量Δu'计算式为：

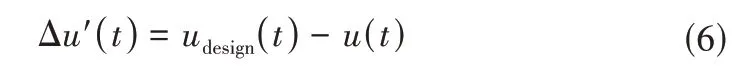
综合前馈和反馈后的控制过闸流量为：

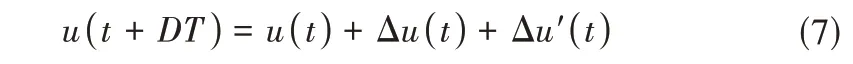
计算得到控制过闸流量后，需要根据当地闸门过流特性反算出符合该过闸流量的闸门开度，然后让执行机构（人工∕自动）执行闸门动作。

式中：G为闸门开度，m；F为当地过闸流量-闸门开度计算公式。

整体控制逻辑见图1：位于渠池下游控制点的水位传感器将监测的下游水位实时反馈给PI 反馈控制器，计算得到相应的反馈流量增量，加上前馈校正流量，两者之和即为该时刻的流量变化量，可得下一时刻的流量，按此流量反算出相应的闸门开度，指导当地人工或者电机执行，以达到控制下游水位在目标值附近的控制目的。其中，PI 控制器计算逻辑见图2。

图1 渠道控制结构示意图Fig.1 Schematic diagram of channel control structure

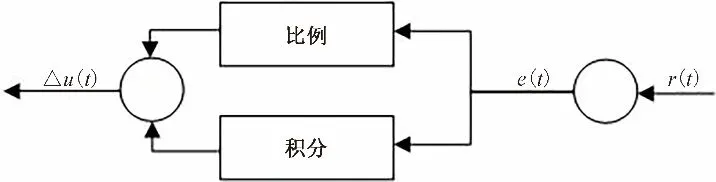
图2 PI控制器计算示意图Fig.2 PI controller calculation diagram

1.3 多目标选取

下游常水位运行模式中，控制对象是每个渠池的上游闸门，控制目标是使该渠池下游水位保持在目标值附近（目标值通常为设计水位，即恒定常数），见图3。

图3中，通过控制闸门维持下游水位在目标值附近，保持为常数。Qmax为渠道加大流量，对应的折线为加大流量下的水面线；Q0为最小流量，一般是生态流量，其对应着最小流量下的水面线。

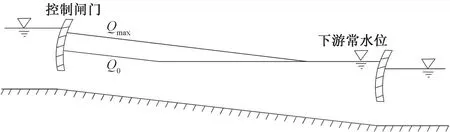
图3 下游常水位控制模式示意图Fig.3 Schematic diagram of downstream normal water level control mode

灌溉渠道系统中的分水建筑物大多为分水闸，由于经济性和实用性，分水闸闸门要保持过流稳定，就要求闸前水位尽量保持在恒定值，也有利于减少分水闸闸门动作调整量。因闸前壅水效应的存在，渠池下游段通常能保持较为水平的水位，所以大多数分水闸都分布在下游段，这就要求闸前水位要尽量保持在一个恒定值，才能保证供水的精确性和稳定性。

在衡量供水渠道系统的控制代价方面，渠道系统通过控制闸门开度来调整过闸流量，进而控制渠池下游水位，而闸门动作需要人力启闭，半自动电力辅助启闭，或者全自动电动闸门启闭，需要消耗的人力和电力就是主要的运行代价。另外，闸门动作量越大，动作次数越频繁，相关的部件磨损就越快。与此类似，在下游常水位的主要目标之外，从安全性和稳定性来考虑，通常希望流量变化量不要过大。

因为控制参数变化会导致系统的控制结果在不同方面的性能上发生变化，并且这种变化通常是互相矛盾的，这就需要提出一个兼顾各方面控制性能的综合性能指标，来衡量、评价其控制结果，进而优化控制参数。针对供水渠道系统，从水位、流量、闸门开度和稳定时间4 个方面，选取以下5 个性能指标作为优化目标，用于供水渠道系统PI 控制参数优化[13]。

（1）最大绝对误差MAE（Maximum absolute error）描述了水位波动极值与目标值的差距，用于衡量水位控制的安全性：

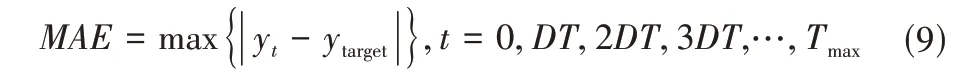
式中：yt为t时刻下游测量水位，m；ytarget为控制点目标水位，m；Tmax为总仿真时长或总运行时长，min；DT为测量水位采样步长或仿真设置步长，min。

（2）绝对值误差积分IAE（Integral of absolute error）描述了系统过渡过程中水位波动的累积量，用于衡量水位控制的平稳性：

（3）绝对流量变化积分IAQ（Integrated absolute discharge change）描述了系统过渡过程中流量变化的累积量，用于衡量流量控制的平稳性：

式中：t1为取水口开始取水时刻，即系统开始发生变化的时刻，min；t2为系统进入稳定状态的时刻，稳定状态一般指水位变化和闸门动作都在t2时刻后一直小于某个设定阈值的状态，min；Q(t)为t时刻渠池上游闸门过闸流量，m³∕s。

（4） 绝对闸门开度积分IAW（Integrated absolute gate movement）描述了系统过渡过程中闸门开度变化的累积量，用于衡量闸门控制的平稳性：

式中：W(t)为t时刻渠池上游闸门开度，m。

（5）稳定状态过渡时间Tstable（Time of transition to stable state）指系统从受外部扰动导致状态开始变化时，受控制算法进行控制应对扰动，直到回复到稳定状态时所用的时间：

可以看出，上述5 个优化目标都采用最小化的优化选项，即优化目标数值越小，则表示系统对应的性能越优。

1.4 基于改进雷达图的综合指标计算

在确定供水渠道系统控制性能评价的多个目标后，需提出一个综合指标的计算式来对上述5 个性能指标进行综合计算。本文借鉴用雷达图来描述系统控制综合性能的思路[16]，改进了雷达图绘制中的数据处理方法，提出采用各项性能指标与初筛样本平均值之比作为雷达图中心到各顶点的距离，并以该改进后的雷达图面积作为综合指标。

上述各优化目标的指标量纲不同且数值数量级差别较大，直接使用会对优化结果的有效性和均衡性造成影响[13]。例如，某一指标的值远大于其他指标，则优化结果就会明显倾向于使得该指标最小的优化方向，而忽视了其他指标，导致优化后控制参数过度追求该方面的控制性能，而在其他方面的性能明显低于期望。为消除上述差异对优化结果的影响，需要对优化目标进行标准化处理。

在数据处理之前，需要先得到符合基本管理要求的初筛样本。初筛样本是指符合初步筛选标准的控制参数样本及与之相应的过程数据及其计算得到的性能指标。初步筛选的标准一般为，水位不超过设计超高，流量不超过设计流量且不低于生态流量，闸门开度变化在允许值上下限内等。具体数值视渠道规模、工况类型和管理要求而定，后文将针对具体算例进行说明。

数据标准化最常用的方法是min-max 标准化法和Z-score标准化法[17,18]。但前者要求确定各项性能指标的最小值和最大值，而控制对象为渠道系统这一复杂非线性系统时，难以给出其在水位、流量等方面的指标极值，故不适用；后者利用样本均值和方差进行标准化处理后的数据弱化了原数据的直观意义，且计算结果有正有负，而负数无法在雷达图上表示，也不适用于本文对象。因此，在标准化处理时，本文提出使用初筛样本平均数作为分母进行标准化处理，即：

式中：X为性能指标原值；Xˉ为初筛样本该项性能指标的平均值；X'为处理后的性能指标计算值，作为雷达图的绘制依据。

将标准化处理后的各项优化指标用于绘制雷达图，见图4。定义雷达图中心到各顶点的距离为l，其长度为该指标与初筛样本平均值之比（l＞0），中心与各顶点连线的夹角相等，均为θ=72°。

图4 综合性能雷达图Fig.4 Comprehensive performance radar chart

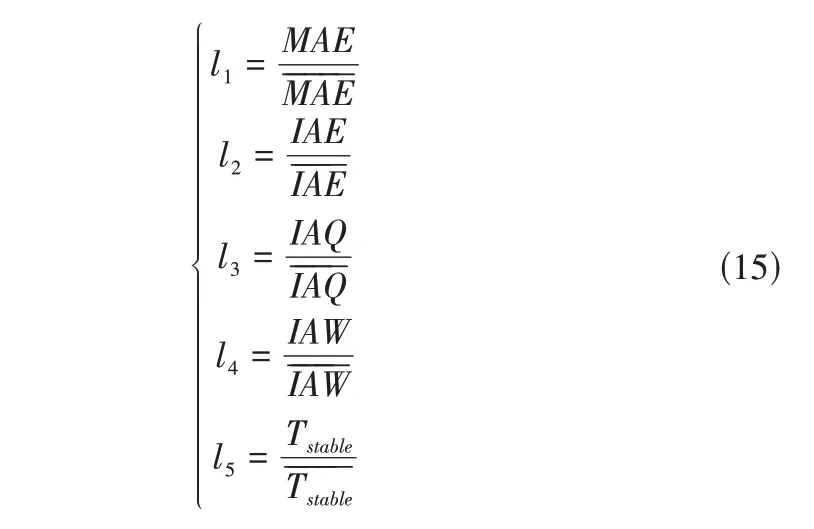
本文创新地提出用初筛样本平均值来进行标准化处理，其主要优势有：其一，平均值更能代表初筛样本参数组合的平均表现，而管理者通常希望得到的优化结果能都在各方面都优于平均表现。用指标原值与平均值之比绘制雷达图，当中心点到该方向顶点距离为l=1 时，代表着该项指标等于样本平均值，而l＜1 时，表示该项指标优于平均表现，符合管理者对于“各项指标均较优”的期望。若采用原值与最大值之比，则所有情况均满足0＜l＜1，不能反映出管理者的期望；其二，采用样本平均值比用最大值更可靠，因为最大值远离样本，其分布存在较大的不确定性，而平均值受样本单值分布的影响小，所以将平均值用于性能评价的参考具有更好的可靠性；另外，如果采用最大值，部分指标的最大值均远离样本中心，会导致绘制所得的雷达图各段l长度过小（＜0.5），不利于结果的呈现。综上，用初筛样本平均值来进行标准化处理在代表性、可靠性和结果呈现3个方面都具有优势。

基于改进后的雷达图，本文提出用该图形面积ARD(Area of radar diagram)作为渠道控制性能综合评价的指标，其计算式如下：

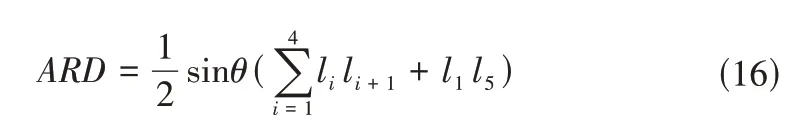
雷达图面积受l1，l2，l3，l4，l5的共同影响，能够全面、综合地反映控制性能的优劣。从运算法则来看，直接用各项指标之和作为综合指标，容易出现“大数吃小数”的现象，弱化了数值较小的指标的影响力；用各项指标之积作为综合指标，容易过度强化了变异幅度大的指标的影响力；用雷达图面积ARD作为综合指标，其计算式包含加法和乘法运算，能够改进简单直接的加和、乘积作为综合指标的缺点，如避免纯加法运算导致“大数吃小数”[19]。因此，所提出的综合指标ARD能够兼顾不同数值大小和变异范围的各指标的影响，更加合理地评价综合性能。

2 结果与分析

2.1 测试算例——漳河灌区四干渠

测试算例所用的渠段取自漳河灌区四干渠，起始四干进水闸，终至田家冲节制闸，总长13.62 km，由5 个节制闸划分为4 个渠池。其渠道系统示意图见图5，仿真渠段几何参数及水力参数见表1。

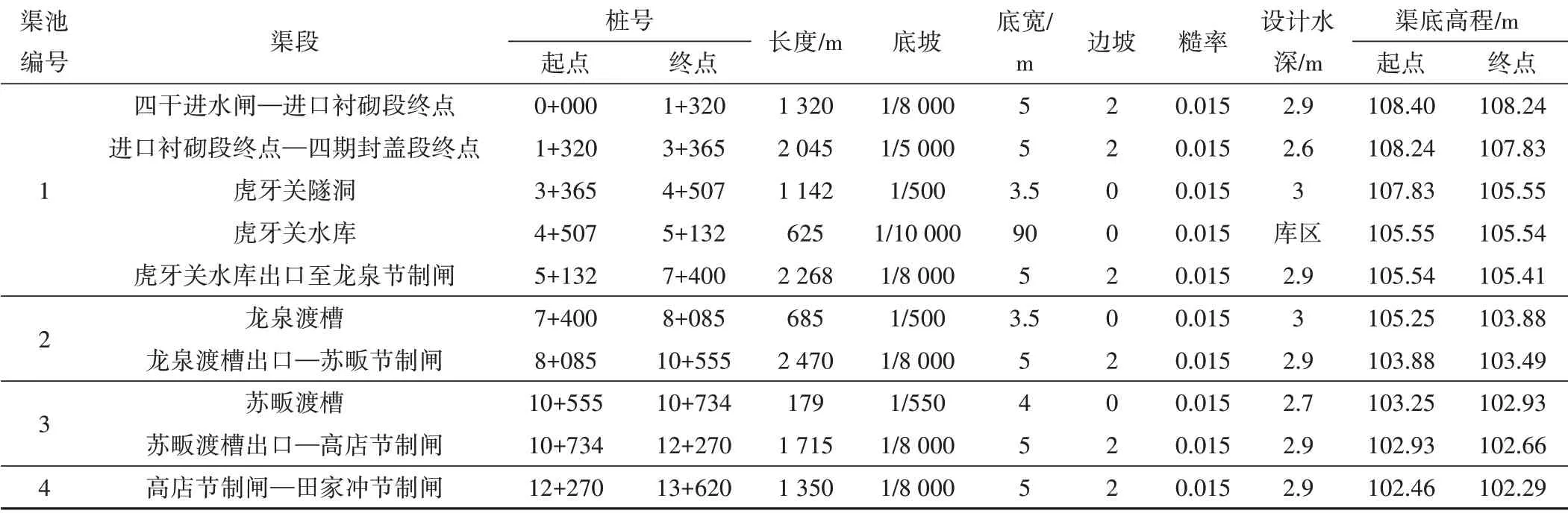
表1 漳河灌区四干渠参数表Tab.1 Parameter table of the fourth main channel in Zhanghe Irrigation Area

图5 漳河灌区四干渠示意图Fig.5 Schematic diagram of the fourth trunk canal in Zhanghe irrigation area

根据四干渠进口闸2019 年流量监测记录，在5-8 月供水时其特征流量为6 m³∕s。又根据位于渠池3 下游的高店分水口设计流量为2 m³∕s，设置典型供水工况为T=2 h 时，高店分水口开始阶跃分水。总仿真时长为6 h，仿真步长为DT=3 min。

仿真平台在渠道内采用一维圣维南方程组来描述水力特性。因缺少各闸门过流实测率定数据，渠池间的节制闸过闸流量计算式用美国中亚利桑那调水工程CAP 公式描述其过流特性。CAP公式如下：

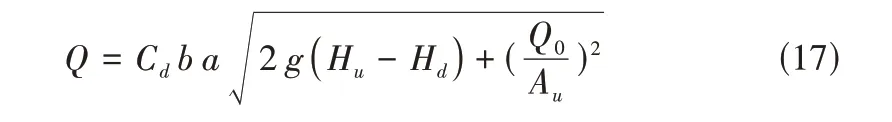
参数优化方法采用基本的网格法，以便看出各指标和综合指标的分布规律。网格寻优法主要是通过选择参数空间中的代表点来代表一定区间的参数空间，从而避免了对参数空间的全局搜索，进而减少了计算成本，以在一定程度上寻优得到合适的参数。本算例中初次优化网格大小为1，二次优化网格大小为0.1。

根据四干渠的规模大小和设计工况的流量变幅，本算例中对控制参数初步筛选的标准为：下游水位不超过目标水位3 cm，末尾渠道（渠池4）流量不少于3.5 m³∕s。本算例仅对水位超高和下游最小流量要求作为筛选标准，对于其他工程，还可以考虑闸门运动限速，最低水位要求等等。另外，因四干渠流量设计值较大（33 m³∕s），其运行流量远小于该设计值，故不需限制。

因评价对象为多渠池系统，而每个渠池都有对应的性能指标，故在计算系统的整体性能指标时，最大水位偏差和稳定过渡时间取4个渠池的最大值，水位偏差累积量、流量变化累积量和闸门动作累积量取4个渠池的平均数。

2.2 基于综合指标的多目标优化结果

初次优化网格范围设置为：Kp=1～20，Ki=1～20，共400 个参数组合。采用Matlab 进行水动力过程仿真计算，以及对控制过程数据处理后进行三维曲面图绘制，得到各单项性能指标分布情况见图6(a)～图6(e)。经初步筛选后，将满足标准的初筛样本各单项性能指标的平均值用于标准化处理，计算得到综合指标ARD分布情况见图6(f)。

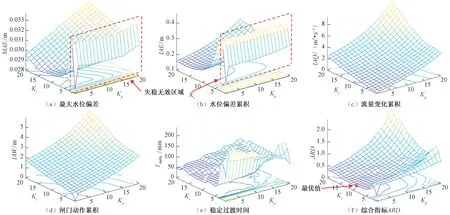
图6 初次优化各指标分布图Fig.6 Indicator distribution of initial optimization

控制参数影响规律分析：最大水位偏差MAE随着积分参数Ki的增大，有先减后增的趋势，与比例参数Kp呈正相关，且其相关性受Ki的影响，Ki越大，MAE随Kp增大而增大的变化速率越大；水位偏差累积IAE的分布规律与前者相似，只是在积分参数Ki＞15 的区域内，IAE随Ki增加而上升的趋势相对不明显。值得注意的是，当Ki=1 与Ki=2 时，由于积分参数过小，PI 控制的积分环节反馈调整量过小，系统无法回到目标稳定状态，因此，此区域为无效区域，其值不参与讨论。流量变化累积IAQ和闸门动作累积IAW由于受过闸流量计算式的关联，有较强相关性，表现在两者的分布极其相似，都与积分参数Ki和比例参数Kp的呈正相关，且相关性也类似。稳定过渡时间Tstable随积分参数Ki有先减后增的趋势，但增长部分不如减小部分的趋势明显，随比例参数Kp的增大而增大，在Ki=10～15，Kp=1～5的部分范围内，Tstable最小，稳定在40 min左右，形成矮平台。综合指标雷达图面积ARD随积分参数Ki的增大而先减后增，随比例参数Kp的增大而增大。

初次优化得到的参数最优组合为：Kp=1，Ki=9，在此参数组合下，综合指标ARD最小，其雷达图面积为0.235，渠道系统在供水工况过渡过程中的最大水位偏差为0.028 8 m，水位偏差累积量为0.192 m，流量变化累积量为0.923 m³∕s，闸门动作累积量为1.06 m，稳定过渡时间为42 min。

二次优化网格范围设置为：Kp=0.1～2.0，Ki=8.0～10.0，共400个参数组合。得到各性能指标和综合指标ARD分布情况见图7。二次优化得到的参数最优组合为：Kp=0.2，Ki=8.2，在此参数组合下，综合指标ARD最小，其雷达图面积为0.224，略小于初次优化所得值。渠道系统在供水工况过渡过程中的最大水位偏差为0.028 9 m，水位偏差累积量为0.196 m，流量变化累积量为0.772 m³∕s，闸门动作累积量为0.952 m，前两者略大于初次优化值，后两者略小于初次优化值。稳定过渡时间为42 min，与初次优化结果一致。

图7 二次优化各指标分布图Fig.7 Indicator distribution of secend optimization

另外，与初次优化结果相比，由于二次优化的参数范围缩小了10倍，导致所有指标的变化范围均有了大幅度的缩小。可以注意到，最大水位偏差分布的极差在0.001 m 以内，水位偏差累积的极差在0.02 m以内，流量变化累积的极差在0.4 m³∕s以内，闸门动作累积变化范围在0.3 m 以内，尤其是稳定过渡时间处于平台期，均为42 min。综合指标的变化范围为0.224～0.226，极差在0.002 以内。这说明了二次优化网格已经足够小，其控制性能指标再减小的潜力已经太小，没有必要进行更加精细的参数优化。

以Kp=0.2，Ki=8.2 为最终优化的控制参数，可以得到渠道系统在供水工况下的下游水位、过闸流量和闸门开度的变化过程如图8～图10 所示。该系统在较短的时间内，付出较少的闸门动作和流量变化量，将水位控制回复到目标值附近，且在此过程中的水位偏差也较小，符合管理者的预期控制效果。注意上述寻优过程均基于仿真计算，其控制效果的进一步提升需要结合更详细的渠道参数，通过多次系统调试运行，才能得到更符合渠系实际情况的控制参数，以达到更优的控制效果[20]。

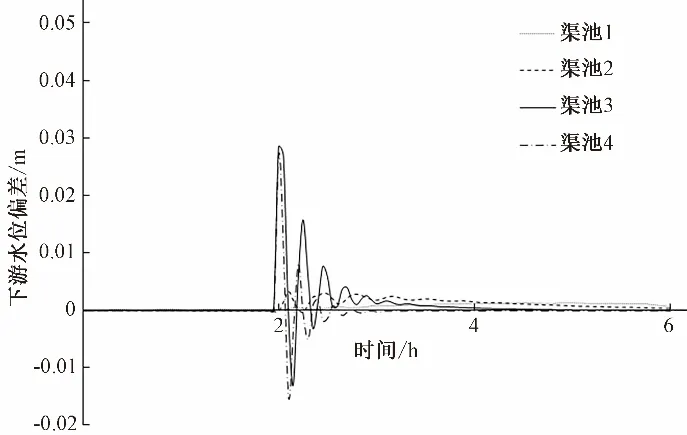
图8 下游水位偏差变化过程Fig.8 Variation process of downstream water level deviation

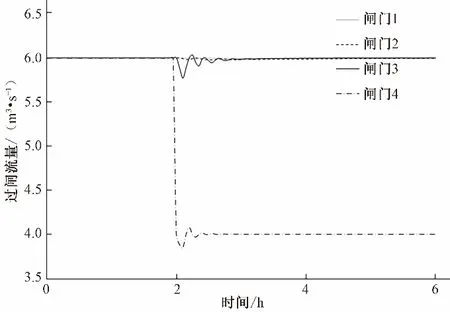
图10 过闸流量变化过程Fig.10 Gate flow change process

3 结 论

本文针对供水渠道系统，选取了最大水位偏差、水位偏差累积、流量变化累积、闸门动作累积和稳定过渡时间5个优化目标，用初筛样本平均值来改进综合性能雷达图，并提出了以该雷达图面积作为综合指标。另外，以漳河灌区第四干渠典型供水工况为例，验证了该综合指标作为PI 控制中参数优化目标的有效性。主要结论如下：

（1）用样本平均值改进了雷达图的绘制方法，相比于用样本最大值进行标准化处理，改进后的方法在代表性、可靠性和结果呈现3个方面都具有优势，能够全面、综合地反映控制性能的优劣。

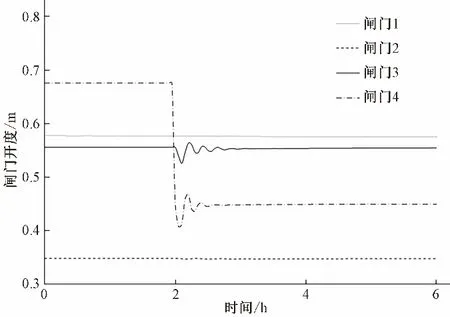
图9 闸门开度变化过程Fig.9 Gate opening change process

（2）提出的雷达图面积综合指标，其计算式包含加法和乘法运算，能够改进简单直接的加和、乘积作为综合指标的缺点，兼顾不同数值大小和变异范围的各指标的影响，能够合理地评价综合性能，可为其他供水渠道的控制和管理提供参考。

（3）以漳河灌区四干渠供水工况为例，应用了提出的综合性能指标雷达图面积，并经两次优化后得到参数组合Kp=0.2，Ki=8.2，能使其综合性能已接近最优。此时雷达图面积最小，为0.224，最大水位偏差为0.028 9 m，稳定过渡时间为42 min，其水位、流量和闸门开度在过渡过程中的累积量均较小，符合控制预期效果。