随机风速背景下风电传动系统机电耦合动态特性研究
张徐
(南京高等职业技术学校,江苏南京 210000)
0 引言
我国领土广阔,风力资源丰富,十分适合风力发电的相关设施建设。在自然环境中随机风速背景下,风电传动系统经常处于变速、随机变载的工作状态,与其他传动装置相比,系统受到的疲劳循环更多,使得风力传动系统故障频发且不易维修[1]。鉴于此,本文对风电传动系统中的机电耦合展开研究,建立随机风速背景下机电耦合动力学模型,研究分析机电耦合对于整体风电传动系统的影响特性。
1 风电传动系统机电耦合动力学建模
1.1 齿轮传动系统扭转动力学模型
常见风电齿轮箱拆解模型图如图1所示,利用综合角位移的性质可以使机械系统坐标与电气系统坐标相同,方便将机械系统与电气系统进行耦合[2-3],使得整个机械系统参数转变为有关轮转角的函数。
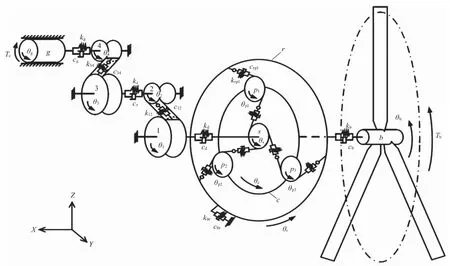
图1 行星轮动力学模型
设定所有构件的角位移与扭矩全部遵循逆时针方向为正方向,齿轮弹性形变以受挤压为正,可以得到齿轮传动系统的动力学方程为:

式中:Jn为系统各构件具有的转动惯量,其中n=s、r、c、pn、1、2、3、4、b、g;θn为系统中各构件具有的角位移,其中n=s、r、c、pn、1、2、3、4、b、g;cn为系统各级轴所具有的扭转刚度及啮合刚度,其中n=b、d、z、g、spn、12、34;rn为系统中各级齿轮半径,其中n=s、r、p、1、2、3、4;δn为系统中各齿轮副啮合弹性变形,其中n=spn、rpn、12、34;mp为系统行星轮质量;rc为行星轮与行星架间间隔;kθr、cθr为系统内齿轮支撑刚度、阻尼;αsp、αrp为齿轮间啮合角;Tb、Te为发电机电磁转矩。
因为齿轮间存在间隙,所以δn应为分段函数形式:
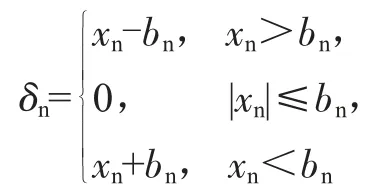
式中:bn为各个齿轮间隙的1/2;xn为齿轮沿啮合线上运动的相对位移。

利用傅里叶级数将时变啮齿刚度进行展开,使之变为与转轮角相关的函数:

1.2 双馈发动机矢量控制模型
双馈电机的数学模型通常是强耦合的,一般将其转换到d-q坐标轴中进行解调[4-5]。默认使用电流从高电位流入的电动机惯例,整体电机数学模型为:

式中:u为电压;i为电流;R为电阻;下标d、q表示坐标直轴与交轴分量;下标s、r表示系统定子侧与转子侧物理量;Lls、Llr为系统定子、转子漏感;Lm为定转子互感;Te为电磁转矩;np为极对数;ω1为体系同步角速度;ωr为转子电角速度。
利用定子电压定向矢量控制技术实施交流励磁,完成发动机恒频变速运行与风能跟踪作用,具体技术原理结构如图2所示。
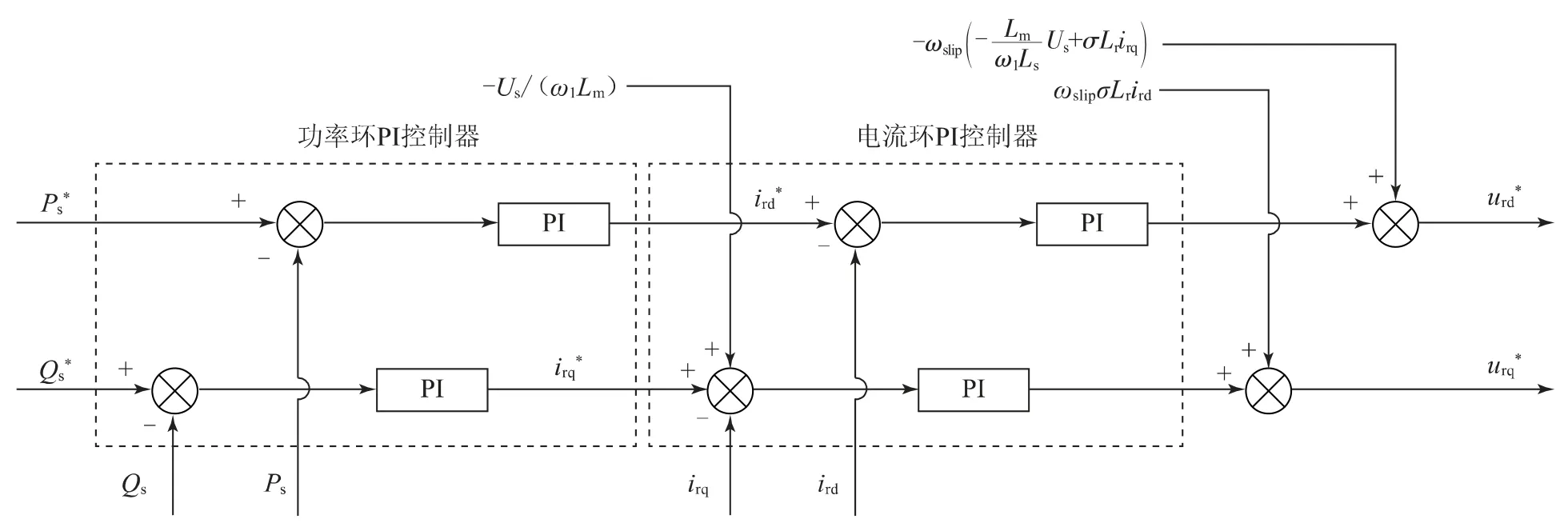
图2 定子电压定向矢量控制技术原理图
2 风电传动系统动态特性分析
2.1 风电传动系统固有特性
由表1中数据可知,风电传动系统振动来源主要有5个方面,其中影响最大的是系统的全局振动,在自然随机风速背景下,风力作用与全局振动间将会产生共振现象。

表1 风电传动系统内固有特性
2.2 随机风速背景下风电传动系统动态响应
利用仿真软件在随机风速背景下对模型进行模拟,平均风速为15 m/s,得到风电传动系统动态响应结果。
利用Turbsim的有关函数模拟50 s的随机风速模型得到图3所示图像,在整个风能转化为电能过程中,叶片不能收集到全部的风能,只能转化一部分,利用风电传动系统收集到的风能在总体中占比计算风能利用系数,如图4所示。
对比分析图3、图4可知,风能利用系数与风速存在部分的反比例关系;对比分析图3、图5可知,实际功率图形与随机风速图形相近,但具有一定滞后现象,所以当现实风速较低时,风能利用系数较大,功率也随之降低。但整体系统运行过程中,风能利用系数长时间处于最大值位置,表明系统基本保持在最大风能跟踪工作。

图3 模拟随机风速曲线
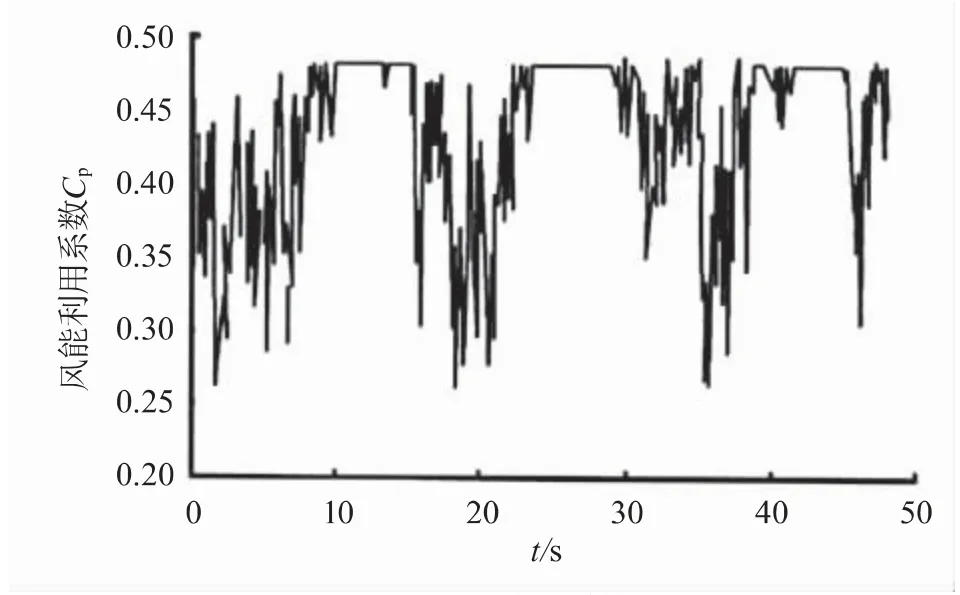
图4 风能利用系数
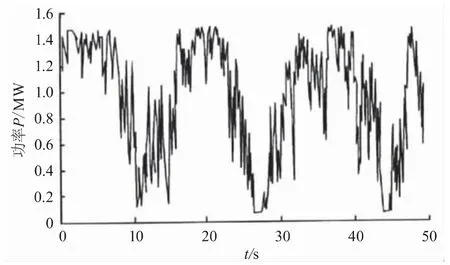
图5 风电传动系统实际功率
具体分析机械系统与电气系统间的关系,二者互相作用主要是通过电磁转矩,根据实验获得的数据建立电磁转矩模型,模拟频谱分析得出结论,发现在耦合过程中,电气系统对于机械系统出现的低频振动现象存在一定的抑制作用。
3 结论
(1)随机风速主要影响风机的运行点位,为了追求风能的最大利用率,风电传动系统一直处在变载状态下,在变载荷的作用下,系统内各种构件的振动与功率变化情况大体稳定,趋势相对一致,但外界低风速与系统全局振动引起的共振现象对动态响应过程影响较大。
(2)在风电传动系统中,机械系统与电气系统具有强耦合性,具体表现为自然随机风速下,机械系统会出现低频振动现象,而这种影响通过耦合效应传递给电气系统产生电磁转矩变化,然后又再次反向影响机械系统。所以,在未来风电传动系统设计过程中,应考虑随机风速背景下机械系统与电气系统耦合产生的影响。

