基于ESF密码算法改进的差分故障攻击①
孔 曼,谭 林,王云丽,龙 敏
1(湖南天河国云科技有限公司,长沙 410100)
2(长沙理工大学 计算机与通信工程学院,长沙 410114)
20世纪70年代中期,分组密码的研究开始兴起,至今信息安全领域的学者们已经取得了许多丰硕的研究成果.近年来,随着物联网的发展,无线传感器网络[1]和无线射频技术[2]的应用愈来愈广泛.轻量级分组密码的出现解决了微型计算设备计算能力有限、低功耗的问题,且其加密速度快、易于硬件实现、能够应用于资源受限的环境中,还具有较高的安全性,所以自问世以来就一直是密码学界关注的焦点.然而,随着信息技术的高速发展,人们对于信息的价值流通具有高要求,虽然这些技术通过开放性的计算机网络实现信息交换和共享,同时也带来了交互效率低、安全保障低等问题.
此外,区块链+物联网[3]是未来的发展方向,区块链技术可以为物联网提供点对点直接互联的方式来传输数据,并且,区块链的密码机制[4]能够为物联网中的信息传输创造安全的环境.尤其在资源受限的物联网节点中需要对数据进行加密时,不可避免地引入具有占用资源少、功耗低、效率高、易于实现等优势的轻量级密码算法,同时对密码算法的安全性提出了更高的要求.
现在的轻量级分组密码算法大都受到DES[5]和AES[6]设计原理的影响,目前已有许多的轻量级密码算法陆续提出,有非常经典的轻量级分组加密算法LBlock[7]、LED[8]、MIBS[9]、KLEIN[10]等,还有近两年的新秀,如Midori[11]、HBcipher[12]、Surge[13]等.然而这些实际用于物联网设备中的轻量级分组密码算法日益凸显出安全漏洞,所以需要对该类算法进行分析研究,不断完善攻击过程与方法,以实现密码算法的更新换代,提升轻量级分组密码算法的防御能力,进一步提升区块链中密码技术的安全性.
故障攻击是一种侧信道攻击方法,于1997年被Boneh 等人[14]提出,并用此方法攻击了基于CRT 算法实现的RSA 签名密钥,意味着首次将密码故障应用于密码分析.同年,Biham 等人首次提出了差分故障攻击[15]并且成功分析了DES 算法.此后,差分故障攻击被广泛应用于公钥密码算法、分组密码算法等等.完成差分故障攻击最重要的一点就是在加密设备中引进故障,如电压瞬变、外部时钟骤变、激光束、X-射线等.差分故障攻击已经应用到了许多的轻量级密码算法分析中.文献[16]以比特为单位进行故障注入,有效地攻击GIFT 算法; 文献[17]针对SKINNY 密码算法提出了恢复主密钥平均需要10 个半字节故障,且通过了大量的模拟验证; 文献[18]利用S 盒的差分不均匀性,在最后一轮注入两次8 个半字节型的故障,快速恢复了最后一轮密钥的信息; 文献[19]提出了随机注入2 字节故障的模型,两对正误密文就可以在不穷举搜索的情况下检索整个128 位AES 密钥; 文献[20]提出了在密钥调度过程中注入一个字节型故障,仅需4 个错误的密文确定整个密钥.
本文通过分析ESF[21]的算法结构,提出了一种差分故障攻击方法.此方法针对结构中按位进行运算的算法具有通用性.此攻击方法的主要思想是,在S 盒运算前注入错误故障,结合差分方程与S 盒在不同故障条件下输出差分不均匀性,进而获取内部状态信息,最后分析得出初始密钥.共需要约10 个故障密文,可将计算复杂度降为222.
1 ESF 算法介绍
1.1 加密流程
ESF 算法是一个基于变种的Feistel 结构的加密算法,轮函数采用的是SPN 代换置换网络形式,其整体结构借鉴于LBlock 算法,其中的置换层是仿照了PRESENT 算法的按位置换形式.
算法流程包含了轮密钥异或、非线性变换、线性扩散、中间状态异或与移位操作.ESF 算法的分组长度为64 比特,初始密钥80 比特,迭代轮数为32 轮.加密流程如图1,数据输入分成左右两个部分,令P=L0||R0表示64 位明文,C=L32||R32表示64 位密文.Ki(i=1,2,…,32)是每一轮迭代加密的轮密钥.轮函数F中包含S 盒非线性变换和P 盒按位置换.

图1 ESF 算法的加密流程
1.2 轮密钥生成
ESF 算法的初始密钥是80 位,记为K=k79k78…k0,初始密钥的左边32 位作为第一轮轮密钥K1,Ki(i=1,2,…,32)是80 位的密钥中间状态,轮密钥生成算法如算法1 所示.

算法1.ESF 算法的密钥扩展方案输入: 80 比特初始密钥.输出: 轮密钥.

1)K1←K;2)for i = 2 to 32 do;3)Ki←Ki-1<<<13;4)[k79k78k77k76] = S0([k79k78k77k76]);5)[k75k74k73k72] = S0([k75k74k73k72]);6)[k47k46k45k44k43] = [k47k46k45k44k43] [i]2;7)Ki←[k79k78…k0];8)Ki←[k79k78…k48].⊕
2 ESF 算法结构分析
2.1 ESF 算法置换层结构分析
ESF 共有8 个S 盒,前4 个S 盒(S7-S4)的输出去往奇数号的S 盒(S7、S5、S3、S1),后4 个S 盒(S3-S0)的输出去往偶数号的S 盒(S6、S4、S2、S0).具体传播位置置换如图2 所示,其中粗线表示有故障的传播,Ii(i=0,1,…,7)是右半明文中间状态的半字节表示形式.
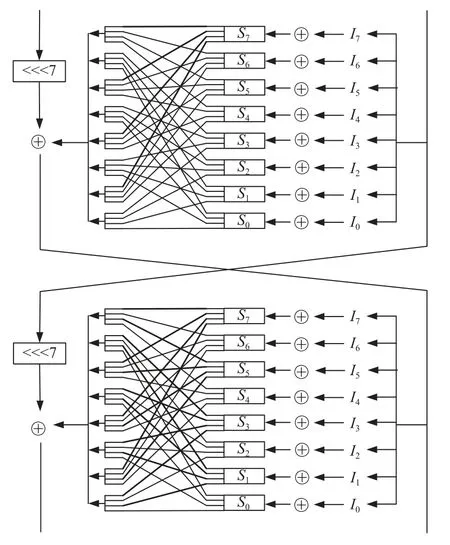
图2 ESF 的置换图
2.2 ESF 算法S 盒差分分布情况
假设a是一个半字节作为某个S 盒的输入.在S 盒输入前,导入随机故障f,即为S 盒的输入差分.f*表示为S 盒的输出差分,则满足差分公式:
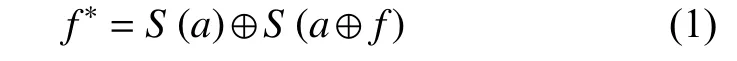
已知每一个输入差分都有一个相应的输出差分,且输入差分有24= 16 种可能,对应的输出差分有4-8 种可能,并且每一对(f,f*)能够得到输入值a的集合,集合内元素的个数为2 或者4.正是由于分布的不均匀性,成为了差分故障攻击的突破口.由于篇幅限制,文中只列出S7盒的差分分布表.ESF 算法S7盒的差分性如表1 所示(ID表示输入差分,OD表示输出差分).
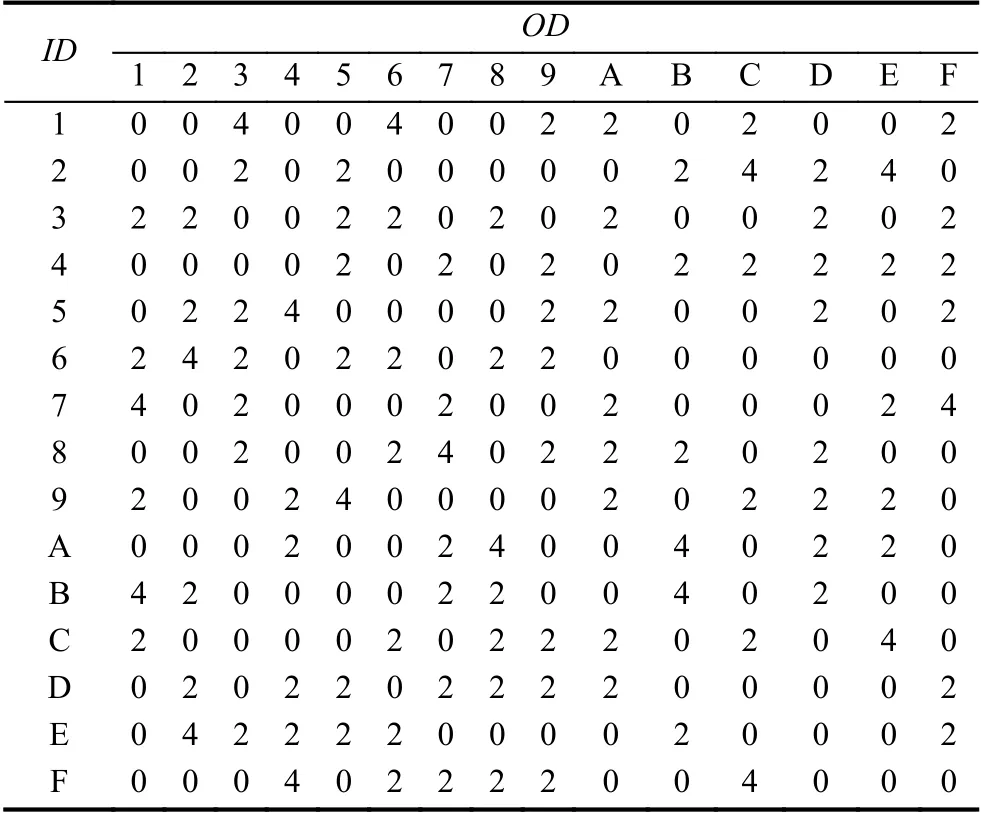
表1 ESF 中S7 盒的差分分布表
2.3 ESF 算法差分扩散规律
已经知道ESF 算法的置换层的基本运算单位是比特.在S 盒运算前随机注入1 比特故障,那么无论在哪个S 盒,输入差分只可能为0001、0010、0100、1 000这4 个中的任何一个,由这4 个输入差分,可列出每个S 盒对应的输出差分,以S7盒为例,表2 列出了S7盒的输入所对应的所有可能出现的输出差分(OD表示输出差分).

表2 ESF 中S7 盒每一个输出差分可能的输入
观察表2 的输出差分,可知,当输入差分仅为0001、0010、0100、1 000 时,经过S 盒后,至少能发生2 比特的故障错误.再分析每个S 盒的可能的输入,可以发现经过S 盒后,发生2 比特和3 比特故障错误的概率较大,且发生2 比特故障错误的概率大于发生3 比特故障错误的概率,发生4 比特故障错误的概率最大也才1/8,因此,在S 盒运算前注入1 比特故障,至少将导致2 个半字节出现错误.本文将以2 比特故障错误进行保守分析.
在S 盒运算前注入1 比特故障,经过3 轮迭代运算后,只导致两个S 盒的输出半字节出现故障错误的平均概率仅为0.019 5,所以在分析过程中可以忽略此种情况.本文将以最后一轮S 盒输出半字节出现故障的个数为3 的情况进行保守分析.
3 ESF 的差分故障攻击
3.1 攻击条件
(1)攻击者有能力选择一个明文进行加密,并获得相应的正确故障密文;
(2)攻击者能够诱导1 比特故障输入到加密的第30 轮寄存器中;
(3)故障位置和值均未知.
3.2 攻击过程及分析
3.2.1 攻击流程
(1)选择明文P进行加密,获得正确密文C.
(2)恢复最后一轮轮密钥,步骤如下:
1)对同样的明文P进行加密,在第30 轮轮函数运行前注入1 比特随机故障到寄存器B30Nj(1≤j≤8,表示在第30 轮、第j个S 盒位置)中,获得错误密文D1.将正确密文C与错误密文D1 进行异或,得到密文差分ΔD1 (此外,密文差分还受上一轮输出的左边32 比特的差分影响,但可直接观察最后一轮右边32 比特密文差分,得到准确的进入逆运算的密文差分),密文差分经过逆P 盒置换,得到最后一轮S 盒的输出差分.
2)查找表2,由最后一轮S 盒的输出差分列出相应S 盒正确输入的候选值.
3)在第30 轮轮函数运算前,多次注入1 比特的随机故障,并重复步骤1)和步骤2),不断缩小S 盒正确输入的候选值的个数,直到剩下唯一一个.此时得到的就是S 盒的正确输入值.
4)最后将正确S 盒的输入值与正确密文的左边32 比特异或,即可得到最后一轮轮密钥.
(3)恢复第31 轮轮密钥,步骤如下:
1)结合最后一轮轮密钥和最后一轮输出,可逆推得到第31 轮正确输出.此时,在第29 轮注入1 比特的随机故障到位置B29Nj(1≤j≤8)中,获得错误密文D2,结合最后一轮轮密钥,可逆推得到第31 轮故障输出.将第31 轮的正确输出与故障输出异或,得到中间状态密文差分(此外,密文差分还受上一轮输出的左边32 比特的差分影响,但可直接观察第31 轮的输出的右32 比特密文差分,得到准确的进入逆运算的密文差分).密文差分经过逆P 盒置换,得到第31 轮S 盒的输出差分.
2)查找表2,由第31 轮S 盒的输出差分列出相应S 盒正确输入的候选值.
3)在第29 轮轮函数运算前,多次注入1 比特的随机故障,并重复步骤1)和步骤2),不断缩小S 盒正确输入的候选值的个数,直到剩下唯一一个.此时得到的就是S 盒的正确输入值.
4)最后将正确S 盒的输入值与正确密文的左边32 比特异或,即可得到第31 轮轮密钥.
(4)恢复第30 轮轮密钥,步骤如下:
1)结合第31 轮轮密钥和第31 轮输出,可逆推得到第30 轮正确输出.此时,在第28 轮注入1 比特的随机故障到寄存器B28Nj(1≤j≤8)中,获得错误密文D3,结合第31 轮轮密钥,可逆推得到第30 轮故障输出.将第30 轮的正确输出与故障输出异或,得到中间状态密文差分(此外,密文差分还受上一轮输出的左边32 比特的差分影响,但可直接观察第30 轮的输出的右边32 比特密文差分,得到准确的进入逆运算的密文差分).密文差分经过逆P 盒置换,得到第30 轮S 盒的输出差分.
2)通过与(3)类似的方法分析出第30 轮轮密钥.
3.2.2 差分故障攻击方法分析
由第3.2.1 节已经知道,在第30 轮S 盒运算前随机注入1 比特故障,在第32 轮至少能得到3 个错误的S 盒输出,在这样的情况下,恢复第32 轮的轮密钥所需要的错误密文则减少到6 个(平均每两对S 盒的输入输出差分所对应的可能输入值的集合能确定唯一的S 盒半字节输入值).
由于是在第30 轮的S 盒运算前注入的故障错误,因此,在恢复最后一轮轮密钥的同时,也可以得到第31 轮中至少12 个错误的S 盒输出,那么只需要在第29 轮的S 盒运算前再注入2 比特的故障错误,得到2 个错误密文就可以恢复第31 轮轮密钥; 在恢复最后一轮轮密钥时,已经得到第30 轮的6 个错误的S 盒输出,在恢复第31 轮轮密钥时,已经得到第30 轮的至少4 个错误的S 盒输出,那么只需在第28 轮S 盒运算前注入2 比特故障,即可恢复第30 轮轮密钥.综上所述,理论上只需要约10 个错误密文就可以恢复最后3 轮轮密钥K32、K31、K30.
3.2.3 密钥推断过程
以下步骤通过恢复出的最后3 轮轮密钥K32、K31、K30,来推断80 比特的完整子密钥,其中“||”表示连接符.
(1)根据密钥的扩展方案,K30是K30的左32 位,K30=K30[0:31] ||K30[47:0];
(2)移位之后:
K30=K30[13:31] ||K30[47:0] ||K30[0:12];
(3)过S 盒之后:
K30=S0(K30[13:16])||S0(K30[17:20])||K30[21:31] ||K30[47:0] ||K30[0:12];
(4)加轮常量之后:
K31=S0(K30[13:16])||S0(K30[17:20])||K30[21:31] ||K30[47:34] ||K30[33:29]⊕i||K30[28:0]||K30[0:12].
(5)K31是K31的左32位,移位之后:
K31=K30[26:31] ||K30[47:34] ||K30[33:29]⊕i||K30[28:0] ||K30[0:12] ||S0(K30[13:16])||S0(K30[17:20])||K30[21:25];
(6)过S 盒之后:
K31=S0(K30[26:29])||S0(K30[30:31] ||K30[47:46])||K30[45:34] ||K30[33:29]⊕i||K30[28:0] ||K30[0:12] ||S0(K30[13:16])||S0(K30[17:20])||K30[21:25];
(7)加轮常量之后:
K32=S0(K30[26:29])||S0(K30[30:31] ||K30[47:46])||K30[45:34] ||K30[33:29]⊕i||K30[28:22] ||K30[21:17]⊕i||K30[16:0] ||K30[0:12] ||S0(K30[13:16])||S0(K30[17:20])||K30[21:25].
K32是K32左32 位, 可以看出K32已知32+13+4+4+5 = 58 位, 剩余22 位未知, 可以通过穷举的方式获得初始密钥, 即初始密钥搜索空间降至222.
4 实验结果与分析
4.1 实验配置
本文使用一台普通的笔记本电脑进行实验,处理器为AMD A4-Series A4-5 000 四核,操作系统为64 位Windows 7 旗舰版SP1,内存为4 GB.采用使用DVEC++ 5.1 软件编程.
4.2 攻击实验结果
本文ESF 算法中的故障注入,是通过编程修改相关语句来实现的.实验过程中的由于样本选取的随机性及样本空间有限,在恢复最后一轮轮密钥的过程中,实际需要的故障密文数量会在理论值周围波动.我们进行了多组实验,现仅列出其中10 组如表3 所示,表4列举了序号1 的实验结果.

表3 差分故障攻击ESF 算法的实验数据
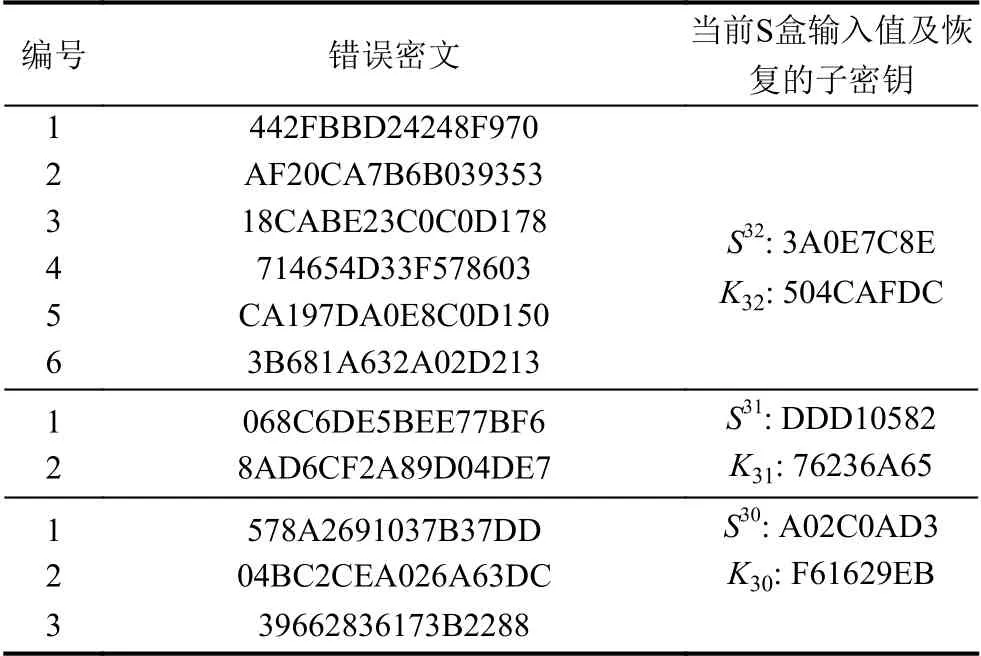
表4 恢复轮密钥的一组实验数据
固定明文和密钥,明文取0123456789ABCDEF,密钥取0123456789ABCDEFFEDC,加密后,获得的正确密文为9F68B9406A42D352.采用本文方法,计算出第32 轮的子密钥504CAFDC、 第31 轮子密钥76236A65 以及第30 轮子密钥F61629EB.这与未注入故障前,正确运行密码算法程序时得出的最后3 轮子密钥一致,验证了本方法的正确性.
根据表3 所列的实验数据,当恢复第32、31、30 轮子密钥时,分别需要进行多次不等的故障注入,但最终的总计结果体现了计算攻击时所需故障密文数量为10.3 个,就能够恢复最后3 轮子密钥.接近理论所需的故障密文数量.
4.3 对比分析
本文针对密码算法ESF 改进的差分故障攻击,其明密文对数量约为10 个,时间复杂度为222,表5 描述了其他针对ESF 算法的攻击方法以供对比.

表5 针对ESF 算法的攻击方法对比表
高红杰等人[22]研究了ESF 算法抵抗不可能差分攻击的能力,基于一条8 轮不可能差分路径,根据轮密钥之间的关系,对12 轮ESF 算法进行了攻击,攻击12 轮ESF 算法所需的数据复杂度为253,时间复杂度为260.23.尹军等人[23]通过建立相关密钥下的MILP 模型,利用搜索到的11 轮相关密钥差分特征,提出了13 轮的相关密钥差分攻击,攻击的数据复杂度为247,时间复杂度为266.李明明等人[24]利用密钥编排算法部分子密钥间存在的依赖关系,给出了ESF 算法的13 不可能差分分析,其时间复杂度为277.39,数据复杂度为261.99个选择明文.徐朋[25]通过在28 到32 轮右半部分导入共约24 次故障,将密钥搜索空间降至222,此方法故障注入要求难度大,需要在轮函数输入前的8 个半字节状态上同时发生故障.
本文方法相较于前3 种方法,有故障注入操作这一技术要求,但是时间复杂度和数据复杂度相对来说降低不少,这得益于差分故障攻击自身的优势; 相较于第4 种同样的差分故障攻击,本文不需要有高要求的故障注入手段,例如,本文不需要限定在一轮的某个位置或者某一部分注入故障,而是可以任意在一轮中随机注入故障,然后充分完整地分析其故障扩散的规律,找到此攻击方法.而文献[25]中,恢复最后3 轮密钥时,将注入故障限定在右半部分密文的每个半字节上,极大地增大了实现难度.因此本文针对ESF 的攻击方法,是目前存在的研究中最优的方法.
5 结束语
本文提出了一种针对置换层为拉线型的密码算法ESF 的改进的差分故障攻击.通过选定最后3 轮,分析故障扩散的程度,分别注入6 次、2 次、2 次故障,共10 次故障,并结合差分表能够分析出最后3 轮轮密钥.结合最后3 轮轮密钥和密钥编排,可将恢复主密钥的计算复杂度降至222.在本章的差分故障分析中,为了保证方法的通用性,且避免最优情况的偶然性,分析过程都是利用概率较大的情况进行分析,例如本文分析中,如果故障影响的比特数越多,密钥分析难度越低,但由于故障传播路径中至少产生2 个比特故障,且产生2 比特故障的概率较大,所以会优先利用实验中产生2 比特故障的情况进行保守分析.这种办法通用性强,还可以用于其他具有类似置换层的密码算法中,分析置换层故障的传播特性和S 盒的差分分布,可得到全部或部分密钥.另外,由于S 盒的一些抗差分性质,导致分析出来的某处S 盒的输入值不唯一的现象.所以,下一步,将针对S 盒的差分分布和其差分均匀度进行研究并改善,加强抵抗此类差分故障分析.

