基于AdaGrad自适应策略的对偶平均方法*

张 旭 韦洪旭

（中国人民解放军陆军炮兵防空兵学院信息工程系 合肥 230031）

1 引言

无论是深度学习还是机器学习中其他方法，针对分类或是回归问题首先都要建立模型随后进行优化求解，求解深度学习网络模型参数可以看作是一个无约束的优化问题，形式如下：

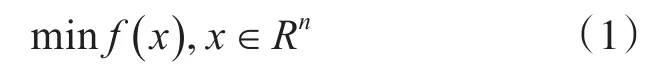
其中f(x)称为目标函数或能量函数，且f(x)为凸函数。

梯度下降法是作为求解上述优化问题的最经典一阶梯度迭代优化方法，每一步都沿着当前梯度方向即损失减小最快的方向迭代，从而不断降低目标函数的函数值，但是传统梯度下降法在每一步迭代求损失函数的梯度时都需要使用整个样本集，得到较高的准确性的同时也伴随着巨大的计算开支。因而传统的梯度下降法不适用于大规模的机器学习问题。这时，人们往往使用随机梯度下降方法（SGD）[1]来代替传统的梯度下降法。SGD利用大规模的机器学习问题数据满足独立同分布假设的特点，在每次迭代中随机抽取1个或者部分样本求梯度，以抽取样本的梯度作为整个数据集梯度的无偏估计，大大降低了计算的复杂度[2]。但是，SGD在每次迭代中只使用当前梯度信息，且由于样本的随机性，收敛过程中存在明显的震荡。2009年，Nesterov在文献[3]中指出SGD的固有缺陷，即收敛过程中新的梯度信息获得不断衰减的步长致使后期收敛缓慢的问题，由此提出了对偶平均方法（DA）。DA克服梯度下降法由于引入衰减步长而导致的固有弊端，具有步长策略灵活的特点，同时，由于每次迭代都利用过往梯度的信息，目标函数值在迭代过程中不会出现剧烈震荡，算法具有较好的收敛稳定性[4]。此后，学者们开始对DA方法展开研究。Xiao在文献[5]中还将DA推广到解决正则化学习问题中去，特别在L1正则化项的情况下，DA较SGD能够更好地保证问题解的稀疏性。Chen等[6]提出最优正则化对偶平均方法（Optimal RDA，ORDA），在DA每步迭代中添加一步子优化问题求解，对一般凸、强凸及光滑问题，均得到O(1/)的最优个体收敛速率。Nesterov等[7]在DA的基础上添加线性插值策略，也得到一般凸问题O(1/)的最优个体收敛速率。曲军谊等[4]进一步证明了对偶平均方法具有与梯度下降法相同的最优个体收敛速率O(lnt/)。可见，无论在算法收敛稳定性还是收敛速率上，DA方法都具有良好表现，而对其的改进仍留有空间。

在深度学习中由于优化问题维度较高，任何单一的人为指定步长都不可能同时满足各个维度的不同要求，因此各个维度需要指定各不相同的步长，因此必须进行昂贵的超参数搜索[8]，由此对深度学习自适应方法的研究成为当前的主流方向之一，形成了 AdaGrad[9]、Adadelta[10]、RMSProp[11]、Adam[12]等一系列自适应优化算法。本文旨在将AdaGrad自适应方法与DA方法相结合，保留DA方法优势的同时，应用自适应矩阵调整步长，使其也能够适应当前深度学习的发展趋势，形成一种自适应的对偶平均方法（AdaDA）。

2 优化算法简要介绍

本节主要对SGD、DA以及AdaGrad算法进行必要的介绍，说明它们在求解式（1）问题的主要差异。我们首先对符号进行明确，k表示算法的迭代步骤，gk表示凸函数f(x)在xk处的梯度∇f(xk)或凸函数f(x)在xk处的次梯度，即gk∈∂f(xk)。

2.1 随机梯度下降法

SGD的迭代过程如下：

其中γk为步长或学习率。一般时，达到收敛。

2.2 对偶平均方法

DA的迭代过程如下：

其中λk为对历史梯度的加权，βk+1为步长，ψ(x)为近端函数。在λk和βk+1的选择上，DA具有灵活的步长策略。基本型的DA方法，即，为了方便与式（2）比较，其可以写为

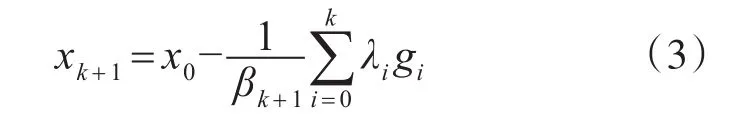
2.3 AdaGrad算法

过去的许多优化算法往往在步长或者学习率上采用的都是常数，对梯度的每一维都进行相同的步长更新。但事实上，样本在不同特征（梯度的不同维度）上的变化速度往往是不相同的，有些维度上梯度信息更新的过快，有的维度上梯度信息更新的过慢，自适应方法的主要思想就是结合历史梯度信息在不同维度上的变化速度给予不同的步长或权重，对变化快的给予较小的权重限制更新速度，对变化慢的给予较大的权重加快更新速度。

AdaGrad第一次使用对角矩阵来对梯度的不同维度分配不同的步长，其他许多自适应方法的研究都是在AdaGrad的基础之上。其迭代过程如下：

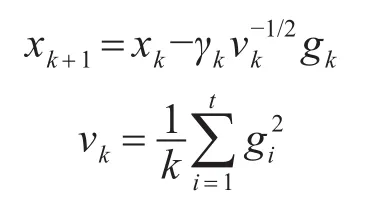
3 AdaDA算法分析

3.1 步长策略

3.2 自适应矩阵的引入分析

3.3 AdaDA

4 实验

本节通过凸优化实验来检验AdaDA算法的可行性与收敛效果。

4.1 实验模型和数据集

凸优化实验中的问题模型，为支持向量机中常见的hinge损失，所采用的6个标准数据集，分别为astro，CCAT，covtype ，ijcnn1，rcv1，a9a均来源于LIBSVM网站，详细数据见表1。

表1 标准数据集

4.2 比较算法和超参数设置

实验中选取三种目前使用较多且效果较好的算法：SGD算法、AdaGrad算法、Adam算法以及基本型的DA方法与本文的AdaDA算法进行对比。DA算法采用文献[2]中的基本型，其他算法步长及参数设置分别为SGD算法使用，AdaGrad算法使用，ε=1e-8，Adam算法使用，ε=1e-8，β1=0.9，β2=0.99，AdaDA算法使用。对于共同超参数γ，我们采取了从｛1，0.1，0.01，0.001，0.0001｝中线性搜索的方式，并取其中最好的一次实验结果，作为该算法的最终输出。为了降低随机因素产生的影响，各算法在每个数据集上均运行5次，并取平均值作为最后的输出。

4.3 实验效果及结论

图1（a）到图1（f）为六种算法在六种标准数据集下的收敛速率对比图，横坐标表示迭代步数，纵坐标为当前目标函数值与最优目标函数值的差，绿色、黄色、黑色、蓝色、红色曲线分别代表Adam、DA、AdaGrad、SGD、AdaDA 算法。图中可见在迭代10000步后，6种算法在6个标准数据集上都达到了10-4次方的精度，且具有相同的收敛趋势，AdaDA收敛速度相对较快，而且精度相对较高。

图1 六种标准数据集

5 结语

本文提出一种名为AdaDA的自适应对偶平均方法，通过一般凸函数分类优化实验验证了该方法的可行性，达到了预期的实验效果，但尚缺乏理论分析。后续，我们将继续对AdaDA算法的平均收敛速率及个体收敛速率进行理论研究。