方中空夹层钢管混凝土叠合构件抗弯性能研究

李明伦，王庆贺，任庆新，贺洪霞，丁纪楠

(1.沈阳建筑大学土木工程学院，辽宁 沈阳 110168；2.中建二局第四建筑工程有限公司，天津 300457)

钢管混凝土叠合构件因其良好的受力性能在高层和超高层建筑、工业厂房、桥梁工程以及车站站台等结构中广泛应用[1-4]。中空钢管混凝土叠合构件由其发展而来，是将空钢管包裹在钢筋混凝土内的结构形式，这种构件具有自重小、抗弯和抗扭刚度大、防火与耐久性好、施工便利等优点[5-7]。近年来，学者提出了中空夹层钢管混凝土构件，是在两个同轴安置的内、外钢管间灌注混凝土形成的钢管混凝土构件，该构件具有承载力高、塑性和韧性强、耐火性能佳、施工便捷等特点[8]。

已有学者针对中空钢管混凝土叠合构件以及中空夹层钢管混凝土构件进行了纯弯、压弯等静力性能研究。梁荟[5]的试验和有限元研究结果表明，方中空钢管混凝土叠合构件的受弯性能优于普通钢筋混凝土构件；J.Y.Chen等[6]进行了箱型中空钢管混凝土叠合构件试验研究，明确了构件的受弯破坏特征；任庆新等[7]建立有限元模型研究了圆形中空钢管混凝土叠合构件的受弯性能；黄宏[8]通过试验研究指出圆中空夹层钢管混凝土构件具有良好的延性，构件受弯后期跨中挠度很大时承载力仍能增长。

已有研究表明，钢-混凝土组合结构能够发挥“1+1>2”的力学性能。基于此，笔者将上述两类构件进行组合，建立了方中空夹层钢管混凝土叠合构件有限元模型，通过模型受弯全过程的承载力-挠度曲线分析，明确此类构件受弯时的应力状态，进而研究不同参数对构件受弯性能的影响，并验证运用叠加原理计算其受弯承载力的适用性。

1 有限元模型建立与验证

1.1 模型参数

方中空夹层钢管混凝土叠合构件有限元模型由外部钢筋混凝土和内部中空夹层钢管混凝土两部分组成(见图1)。

图1 构件截面形式Fig.1 Cross-section of specimens

模型参数：长度L=2 000 mm，宽度B=200 mm，外钢管直径Do=114 mm，内钢管直径Di=58 mm，内外钢管壁厚均为3 mm(ti=to=3 mm)；内外钢管采用Q355钢材，纵筋采用Φ12钢筋，型号为HRB400，纵筋配筋率为3.04%，箍筋采用Φ6.5钢筋，型号为HPB300，箍筋间距为100 mm；外部混凝土和夹层混凝土强度等级均为C40，混凝土保护层厚度为25 mm。

1.2 材料本构关系

钢管部分的钢材本构采用韩林海[1]推荐的五段式应力-应变关系模型；钢筋部分的钢材本构采用双折线简化的应力-应变关系模型；弹性阶段弹性模量Es=206 GPa、泊松比μ=0.3，强化阶段弹性模量取0.01Es。

笔者采用塑性损伤模型来描述混凝土本构关系，钢管外混凝土的应力-应变关系曲线和弹性模量按文献[11]中规定计算。钢管间夹层混凝土的应力-应变关系曲线和弹性模量按文献[1]中规定计算。混凝土弹性阶段泊松比取0.2。

1.3 模型的建立

1.3.1 单元类型及网格划分

方中空夹层钢管混凝土叠合构件有限元模型见图2。钢管部分采用四节点壳单元(S4R)，单元厚度方向采用9个积分点的Simpson积分；混凝土、端板、加载板和支座垫板部分采用八节点三维实体单元(C3D8R)；钢筋部分采用两节点三维桁架单元(T3D2)。

图2 有限元模型Fig.2 Finite element models

通过ABAQUS的结构化网格划分功能确保网格划分均匀对称；通过使各接触部件间网格尺寸一致且单元节点对应，确保各部件间传力效果良好。内外钢管、夹层混凝土截面环向采用16等分点划分网格；试件外部横向采用8等分点划分网格，纵向采用100等分点划分网格。

1.3.2 界面接触、加载方式及边界条件

钢筋骨架整体嵌在钢管外混凝土内部。钢管与混凝土接触面间法向采取“硬”接触处理，切向采用“罚”函数模拟界面相对滑移，界面摩擦系数取0.6[6]。将端板设为刚体，其与钢管端部采用壳-实体耦合约束，与混凝土端部采用绑定约束，以保证加载过程中钢管和混凝土端部变形一致；钢管与混凝土间设为小滑移，加载板和支座垫板与混凝土间设为有限滑移[6]。

试件采用四分点式加载，试件顶面设有加载板，加载点与加载板顶面中线耦合，采用位移加载的方式施加竖向位移。试件底面设置支座垫板，限制左端支座垫板底面中线X、Y、Z方向的位移，模拟固定铰支座；限制右端支座垫板底面中线X、Y两个方向的位移，模拟滑动铰支座。

1.4 模型的验证

由于缺乏相应的纯弯试验数据，笔者根据研究对象截面特点，视其为方中空钢管混凝土叠合构件与圆中空夹层钢管混凝土构件两部分的叠合(见图3)。通过分别验证图3(b)和图3(c)两部分模型的可靠性，间接完成对图3(a)叠合构件有限元模型的验证。

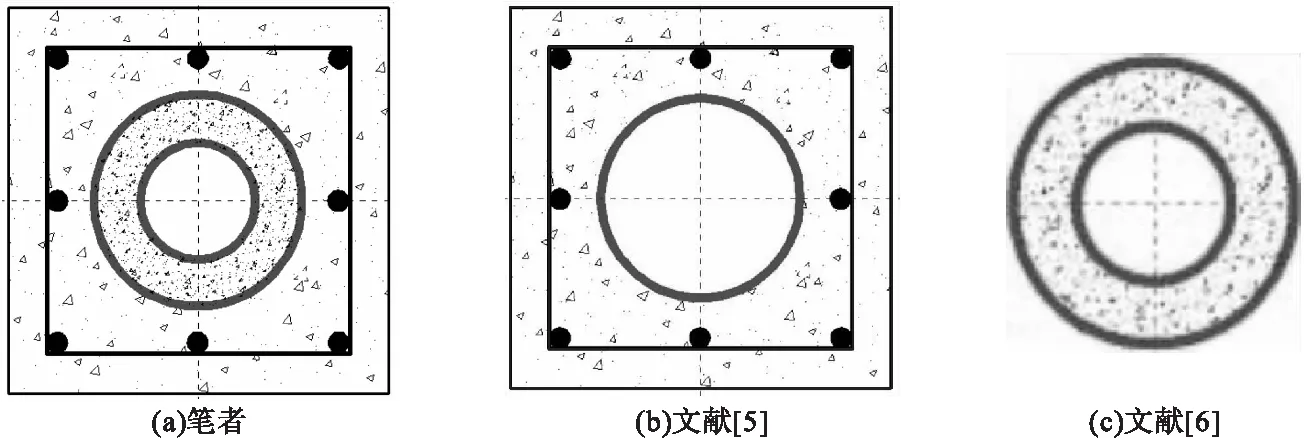
图3 截面叠合形式Fig.3 Intersection combination form

将图3(b)对应模型计算结果与文献[5]中试件sb1、sb2、sb3试验结果对比，荷载-挠度曲线对比见图4(a)，承载力对比结果见图5(a)；将图3(c)对应模型计算结果与文献[6]中试件bcc2、bcc3、bcc4试验结果对比，荷载-挠度曲线对比见图4(b)，承载力对比结果见图5(b)。结果表明，两部分模型计算曲线和试验曲线均吻合较好，承载力相差在10%以内，笔者建立的有限元模型可以用来研究此类构件的抗弯性能。

图4 荷载-挠度曲线对比Fig.4 Comparison of load-deflection curves

图5 承载力对比Fig.5 Comparison of bearing capacities

2 受力状态分析

2.1 荷载-跨中挠度关系曲线全程分析

基于上述有限元模型研究方中空夹层钢管混凝土叠合构件的受弯性能，图6为构件受力全过程跨中承载力-跨中挠度(M-um)关系曲线，图中受力特征点定义如下，特征点A：外部混凝土出现明显开裂，构件刚度开始降低；特征点B：受拉纵筋开始屈服，构件刚度进一步降低；特征点C：外钢管受拉边缘开始屈服，构件刚度继续降低；特征点D：内钢管受拉边缘开始屈服，同时外钢管受压边缘亦屈服，此时构件承载力接近峰值；特征点E：外钢管受拉侧边缘纤维应变达到0.01，此后构件承载力变化趋于平稳。

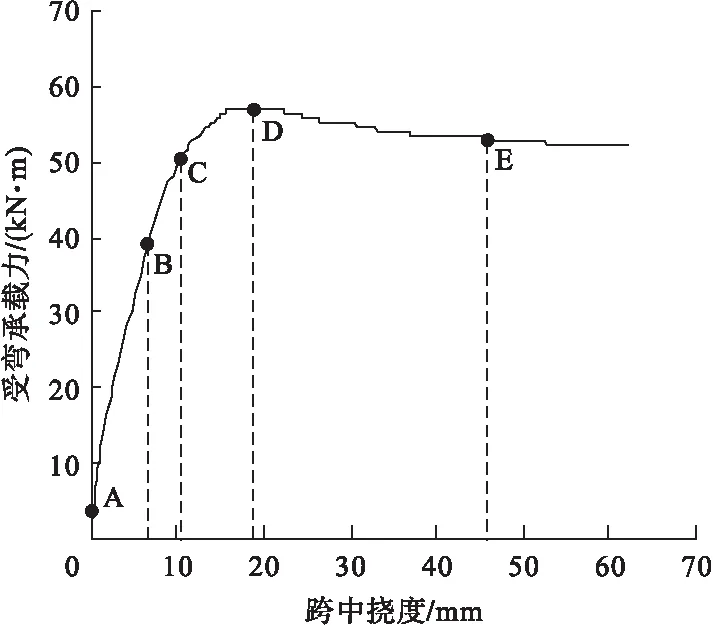
图6 承载力-挠度关系曲线Fig.6 The bearing capacity-deflection curve

2.2 跨中截面混凝土纵向应力应变分布

图6中各受力特征点时的跨中截面混凝土纵向应力和纵向应变分布情况如图7所示，图中fc表示混凝土抗压强度。从图中可以看出，在特征点A时，外部混凝土受拉侧边缘达到开裂拉应变，夹层混凝土开裂晚于外部混凝土；特征点A之后，中和轴(纵向应变为0处)向受压侧上移，混凝土受压区面积减小；外部混凝土受压侧边缘压应变随着跨中挠度增大持续增加，接近特征点C时达到峰值，其中和轴在达到峰值荷载(特征点D)后有所回落；特征点E后，夹层混凝土压应力继续提高，其性能在承载后期得到充分发挥。

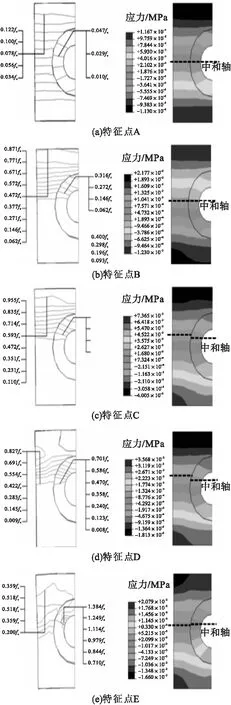
图7 特征点处跨中截面混凝土纵向应力应变分布Fig.7 Distribution of longitudinal stress(S33)and strain(E33)in concrete at mid-span

2.3 钢管与混凝土间接触压力

受弯时方中空夹层钢管混凝土叠合构件中存在多类接触应力，定义外钢管与夹层混凝土接触压力为p1、外钢管与外部混凝土接触压力为p2、内钢管与夹层混凝土接触压力为p3，试件跨中截面不同位置接触点处接触压力随加载过程的变化规律如图8所示。

图8 跨中不同位置接触压力-挠度关系曲线Fig.8 Interaction press-deflection curves of different locations at mid-span

从图8(a)可以看出，加载初期，由于钢管泊松比较混凝土大，横向变形较大，使外钢管与夹层混凝土有分离趋势，p1=0；特征点A～C段，随着夹层混凝土产生塑性变形，泊松比增大，p1随之增大；接近特征点D时，各接触点处p1相差不大；特征点D之后，p1继续增大，接触点1、3处p1较其余接触点增幅变缓；加载末期，接触点5处p1约为接触点1处p1的2倍，这是因为核心混凝土在受拉区具有更大的变形；受压区接触点2处p1增长趋势与受拉区相近，原因是受三向约束的核心混凝土阻止外钢管内凹。

从图8(b)可以看出，p2明显小于p1，外部混凝土开裂后与外钢管分离，导致受拉区接触点4、5处p2为0；特征点A～D段，接触点1、2、3处p2受外部混凝土塑性变形影响，其值在0.3 MPa内变化，后随着外钢管受压侧屈服降至0；特征点D后，p2随外钢管塑性变形增加而增大，并在特征点E前后达到峰值，此时接触点1、3处p2约为0.5p1，接触点2处p2约为0.25p1。

从图8(c)可以看出，特征点B以前，各接触点处p3接近0，原因是夹层混凝土与内钢管弹性受力时的横向变形小；特征点C～D段，p3显著增加，并在内钢管屈服后达到峰值，峰值区间为0.8～1.2 MPa，接触点1、2、3处p3峰值与p2峰值相近，表明核心混凝土可以有效抵抗内钢管变形；此后p3逐渐降低，这是因为外钢管受压侧和内钢管受拉侧屈服后，对核心混凝土的约束作用减弱，内钢管与核心混凝土界面趋于分离。

3 参数分析

笔者选取混凝土抗压强度fcu、纵筋配筋率ρ、纵筋屈服强度fyl、钢管空心率χ、钢管屈服强度fys、截面径宽比Do/B为参数对构件抗弯性能进行研究，试件参数见表1。SF0作为对比算例，纵筋配筋率为2.37%，空心率为0.54，截面径宽比为0.57。

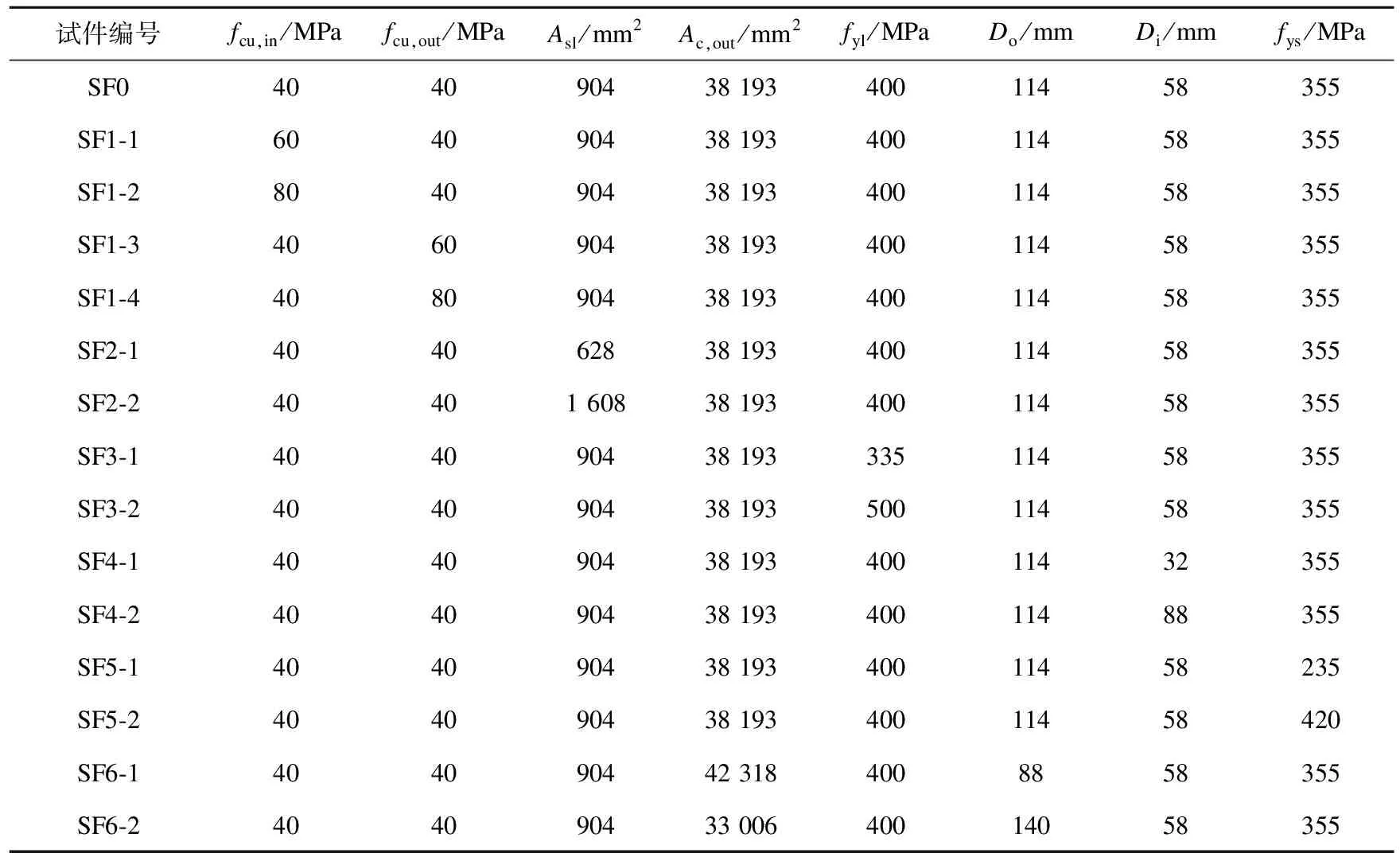
表1 试件参数Table 1 Parameters of specimens

3.1 混凝土强度的影响

图9为不同混凝土强度下试件受弯承载力-跨中挠度(M-um)关系曲线，图中fcu,in为夹层混凝土强度，fcu,out为外部混凝土强度。从图中可以看出，fcu,in由40 MPa提高至60 MPa和80 MPa时，试件抗弯承载力Mu和抗弯刚度Bs的增幅很小，分析原因，夹层混凝土仅有少量区域位于受压区，因而对构件抗弯性能影响有限；fcu,out由40 MPa提高至60 MPa和80 MPa时，Mu由57.2 kN·m增至64.8 kN·m和71.6 kN·m，分别提高了13.3%和25.2%；Bs由1 241.5 kN·m2增加到1 434.0 kN·m2和1 454.4 kN·m2，分别提高了15.5%和17.1%。但抗弯刚度的提升幅度随之明显降低。

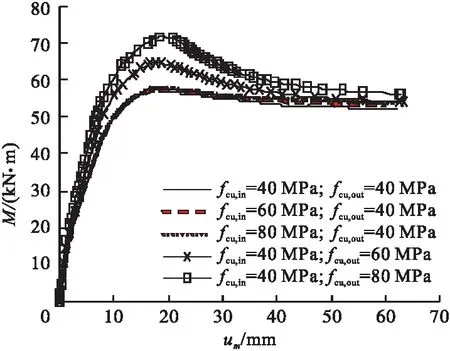
图9 不同混凝土强度下M-um曲线Fig.9 M-um curves corresponding different concrete strength

3.2 钢筋参数的影响

图10为不同纵筋配筋率和纵筋屈服强度下试件M-um关系曲线。从图中可以看出，ρ由1.64%增大到2.37%、4.21%时，Mu由50.4 kN·m增加到57.2 kN·m和72.9 kN·m，分别提高了13.4%和44.6%；Bs由1 171.3 kN·m2增加到1 241.5 kN·m2和1 422.7 kN·m2，分别提高了6.0%和21.5%。表明提高配筋率可显著提高构件抗弯承载力和抗弯刚度，且增幅会随之显著提高。

图10 不同纵筋配筋率和纵筋屈服强度下M-um曲线Fig.10 M-um curves corresponding different reinforcement ratio and yield strength of longitudinal reinforcements

fyl从335 MPa增至400 MPa、500 MPa时，Mu由54.0 kN·m增至57.2 kN·m和61.7 kN·m，分别提高了5.9%和14.3%，增幅不是很明显；Bs由1 200.4 kN·m2增加到1 241.5 kN·m2和1 230.5 kN·m2，增幅不明显，表明纵筋屈服强度对试件抗弯性能的影响较小。

3.3 钢管参数的影响

图11为不同钢管屈服强度和空心率下试件M-um关系曲线。从图中可以看出，将内外钢管fys同时从235 MPa提高到355 MPa、420 MPa时，Mu由52.2 kN·m增至57.2 kN·m和59.4 kN·m，分别提高了9.6%和13.8%，增幅不明显；fys对Bs的影响很小。

图11 不同空心率和钢管屈服强度下M-um曲线Fig.11 M-um curves corresponding different hollow ratio and yield strength of steel tubes

χ由0.30增加到0.54和0.81时，Mu由56.5 kN·m增加到57.2 kN·m和60.3 kN·m，增幅较小。Bs由1 134.4 kN·m2增至1 241.5 kN·m2和1 444.3 kN·m2，分别提高了9.4%和27.3%，增幅比较显著。

3.4 截面径宽比的影响

图12为不同截面径宽比下试件M-um关系曲线。从图中可以看出，Do/B由0.44提高至0.57和0.70时，Mu由51.3 kN·m增加到57.2 kN·m和63.9 kN·m，分别提高了11.5%和24.6%，增幅比较明显，分析原因，随Do增大，外钢管参与受拉的面积会随之增大；Bs由1 213.1 kN·m2增至1 241.5 kN·m2和1 287.2 kN·m2，增幅不明显。

图12 不同截面径宽比下M-um曲线Fig.12 M-um curves corresponding different diameter-width ratio

4 受弯承载力计算

笔者基于叠加原理提出方中空夹层钢管混凝土叠合构件的受弯承载力计算公式：

Mu=Mu,orc+Mu,ihcds.

(1)

式中：Mu,orc为外部钢筋混凝土部分的受弯承载力，参照《混凝土结构设计规范》(GB50010—2010)[11]提供的方法计算；Mu,ihcds为内部中空夹层钢管混凝土部分的受弯承载力，参照文献[6]计算：

Mu,ihcds=rm1Wscmfcy+rm2Wsifsi.

(2)

其中：rm1和rm2为中和轴变化对两部分承受弯矩的影响系数，rm1=0.48ln(ξ+0.1)·(-0.85χ2+0.06χ+1)+1.1，rm2=-0.02χ-2.76lnξ+1.04χ-0.67；fcy和Wscm分别为外钢管与夹层混凝土的组合轴压强度和截面抗弯模量；fsi和Wsi分别为内钢管的屈服强度和截面抗弯模量；fcy参照文献[13]计算：

fcy=C1χ2fyso+C2(1.02ξ+1.14)fck.

(3)

其中，C1=α/(1+α)，C2=(1+αnom)/(1+α)。

采用式(1)计算不用参数下试件受弯承载力，结果见表2。从表中可以得出，式(1)计算结果与有限元计算结果比值的平均值为1.03、标准差为0.08，二者吻合良好。

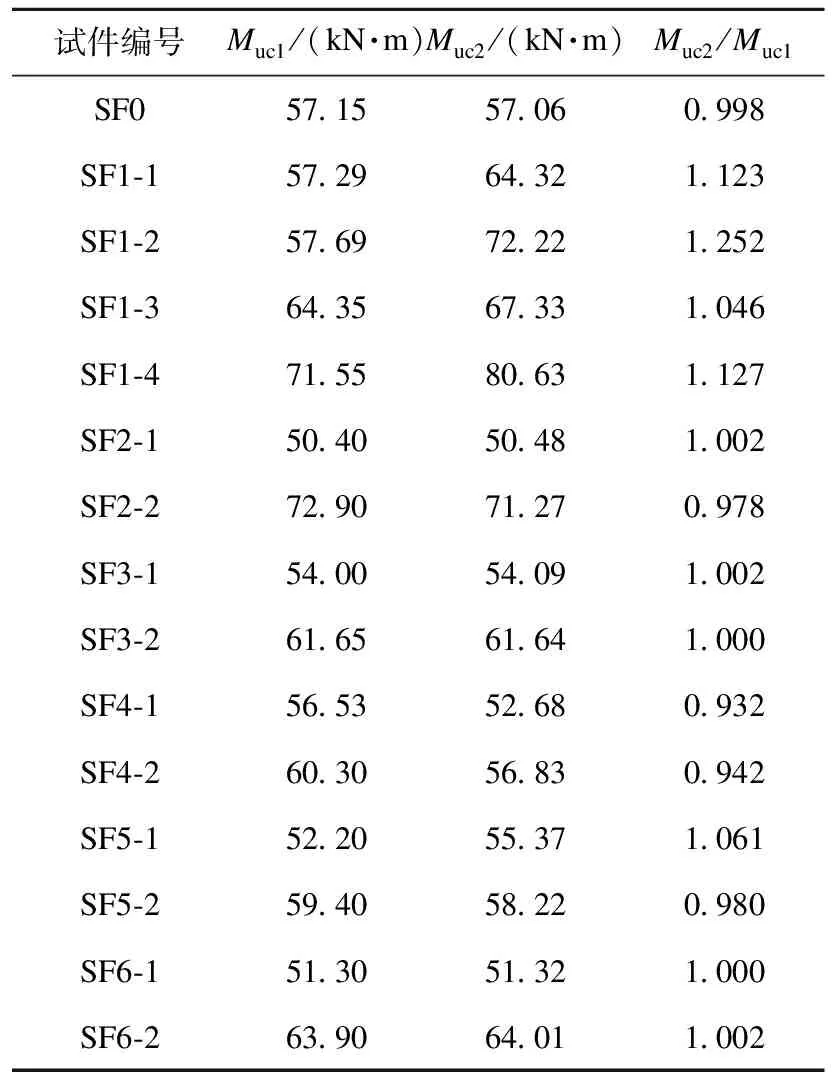
表2 承载力计算结果Table 2 FEM values of specimens

5 结 论

(1)方中空夹层钢管混凝土叠合构件的受弯过程经历了外部混凝土受拉开裂、受拉纵筋屈服、受压纵筋屈服、外钢管受拉边缘屈服、内钢管受拉边缘和外钢管受压边缘屈服、内钢管受压边缘屈服、外部混凝土压溃等阶段，外部钢筋混凝土和夹层钢管混凝土两部分的力学性能都得到了充分发挥，构件具有良好的抗弯性能。

(2)提高纵筋配筋率和外部混凝土强度可显著提升方中空夹层钢管混凝土叠合构件抗弯承载力和抗弯刚度；增大外钢管直径和空心率能够分别提升构件抗弯承载力和抗弯刚度；提高纵筋强度与钢管强度可一定程度提高构件抗弯承载力。

(3)采用叠加原理提出的计算公式可有效计算方中空夹层钢管混凝土叠合构件的受弯承载力。