压接型IGBT 功率模块加速老化试验方法
李标俊,褚海洋,庄志发,文军
(1. 中国南方电网有限责任公司超高压输电公司天生桥局,贵州 兴义 562400;2. 荣信汇科电气股份有限公司,辽宁 鞍山 114051)
0 引言
压接型绝缘栅双极型晶体管(insulated gate bipolar transistor ,IGBT)在柔性直流换流阀中被广泛应用。针对压接型IGBT 的老化测试已有相关研究,但测试器件的散热条件与实际工程应用还有一定差距[1-4]。现有研究对采用压接型IGBT的柔直功率子模块进行可靠性试验的经验不足,亟须针对压接型IGBT 的加速老化方法进行研究。
文献[5]从压接型IGBT 的封装方面进行了老化机理研究。目前商用压接型IGBT 常采用多芯片并联的封装形式,该形式使得压接型IGBT的电-热性能对施加的压力非常敏感[6-7]。文献[8]提出了不同结构设计的IGBT,其最佳压力范围必然有所不同,建议要在被试器件测试时对压接力进行匹配。文献[9]研究了单芯片和多芯片在压接力下的有限元模型,为规定器件压接力度合理范围提供了依据。文献[10-11]认为压接型IGBT开关瞬间的集肤和邻近效应将导致各芯片电流通路阻抗不同,使得电流密度的分布极不均匀,影响器件可靠性。要考察器件的长期可靠性,则须为器件设计功率循环试验。传统的功率循环试验设计往往基于功率变换器的可靠性评估模型。文献[12]设计的老化循环试验包括恒载荷和多段阶梯载荷等功率循环方式,通过壳温测量反映了试验实时工况。文献[13-14]完成了压接型IGBT 器件的柔直换流阀功率模块的仿真分析。
综上,基于老化循环类型少、周期等参数定义难等问题,本文提出了压接型IGBT 功率模块加速老化试验方法,推导出冲击循环、高温循环、温度循环与功率循环等形式的老化试验,得到了不同试验中决定老化循环方式的波动幅度、周期等关键参数。
1 老化循环试验方法原理
老化循环试验拓扑如图1 所示。从图1 可以看出,2 个功率模块之间通过负载电抗相连。对于压接型IGBT 来说,无论是温度循环还是功率循环,其电流和损耗都呈周期性[15-17]。本文将周期性损耗的平均值作为衡量疲劳应力的依据。若要从外部分析热应力对器件造成的疲劳老化,则要获得IGBT 芯片的结温,并要建立芯片到散热器的热阻抗模型。目前结温计算依赖于材料热力特性及复杂模型参数等数据支撑[18]。对热阻抗模型等效简化是提高热应力分析可行性的有效途径。另外对于热阻抗模型而言,文献[19-20]提出了压接型功率器件热阻测量方法,具有借鉴意义。
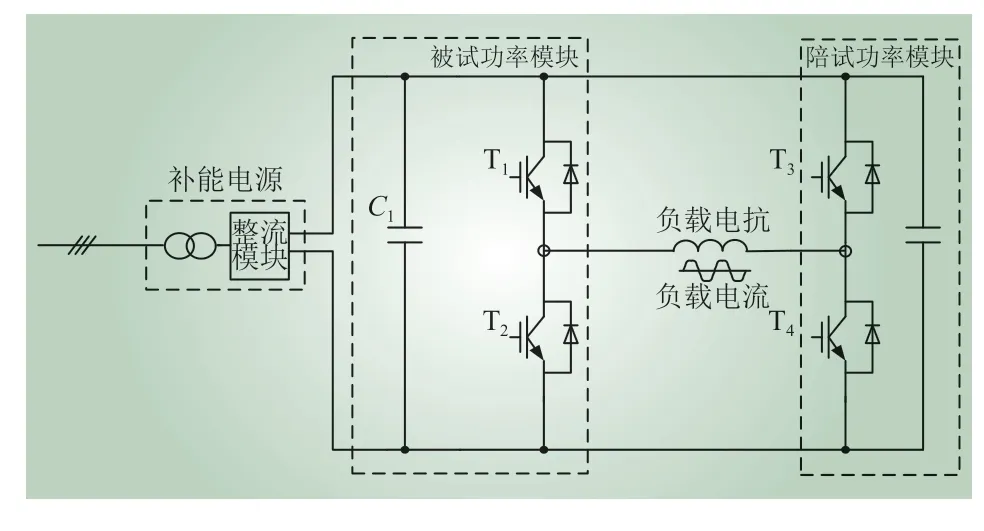
图1 老化循环试验拓扑Fig. 1 Topology of aging cycle test
温度波动值大小直接决定了器件可耐受的循环次数,结温波动越大,循环次数越少。基于结温循环的原理并结合IGBT 及其电力循环试验标准[21-25],本文提出了冲击循环、高温循环、功率循环和温度循环等老化形式来对器件的不同部位进行耐久性和可靠性测试。
压接型IGBT 各层结构如图2 所示。本文采用功率器件Cauer 模型以直接反映芯片内部不同结层不同材料的热特性,并确定了4 种加速老化试验的考察原理,如表1 所示。

图2 各层结构Fig. 2 Structure of each floor

表1 试验项目Table 1 Test items
2 老化方法及热计算
本文通过对试验目标进行等效,4 种试验项目类型如表2 所示。

表2 试验类型Table 2 Test types
(1)冲击循环试验中IGBT 需经受短路电流,产生的损耗在短时间内会以焦耳热形式致使芯片结温瞬时升高,温升值为
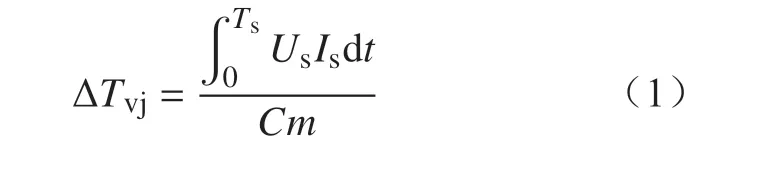
式中:ΔTvj为IGBT 芯片的实际温升;C为芯片比热容;m为芯片质量;Us为模块电压;Is为冲击电流;Ts为冲击脉冲持续时间。
短路工况时间极短,只有10 μs 左右,则只考虑IGBT 自身热容,因此可将其模型简化为热阻抗模型。在短路期间短路冲击产生的热量几乎全部集中在IGBT 芯片内部,因此IGBT 芯片热容Cj为

式中:cth为芯片材料的容积比热容;d为芯片厚度;A为芯片的面积。
(2)功率循环试验中,IGBT 器件热阻抗模型可看作一个n阶网络。对于周期性的方波输入,其输出为无数个脉冲信号的叠加。当t=T/2 时,器件结温到达最大值Tmax。当t=T时,器件结温达到最小值Tmin。器件结温波动ΔT为
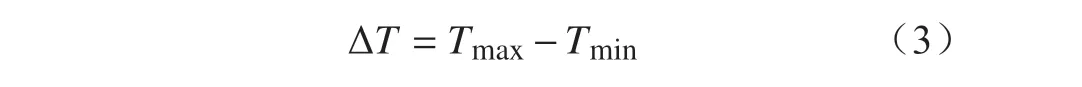
器件结温波动与输出频率f密切相关,如进一步考虑进水温度变化,则最大结温Tmax为
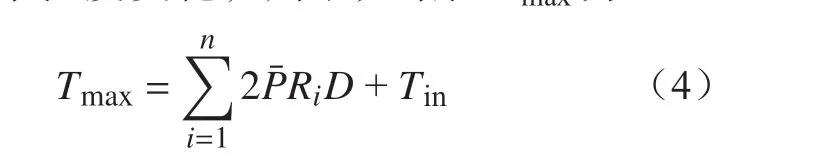
式中:P¯ 为脉冲功率均值;Ri为第i级热阻抗网络热阻;D为结温算子;Tin为功率模块水冷进水温度。
功率循环试验负载及器件结温变化如图3 所示。让结温达到器件最大允许结温,结温波动为60℃,周期小于10 s,则可计算功率循环所需的电流大小。
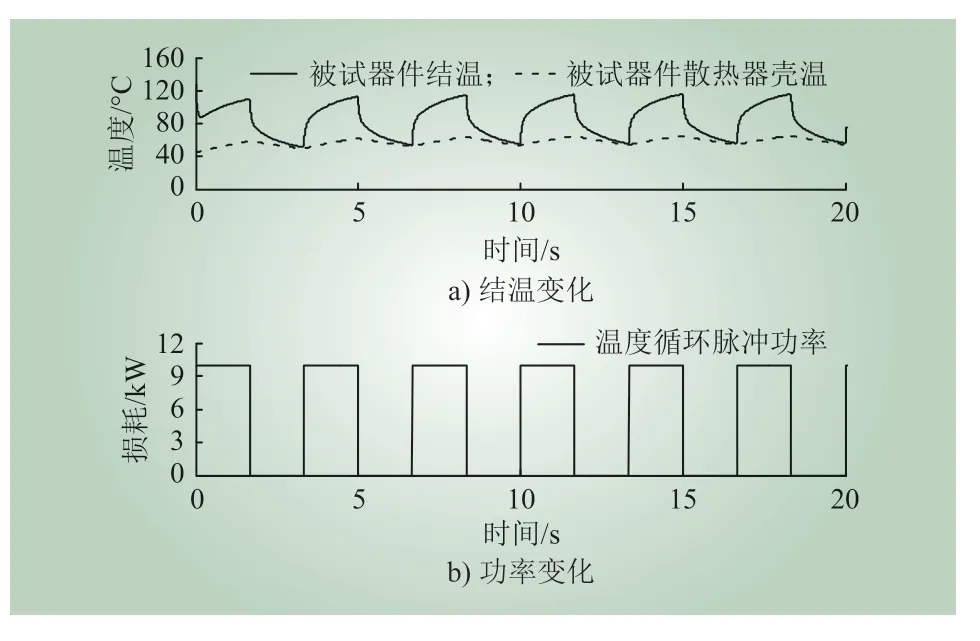
图3 功率循环试验结果Fig. 3 Results of power cycle test
(3)在恒定高温试验中,采用恒定负载,负载调制电流设置为定值。恒定高温试验器件最大结温为
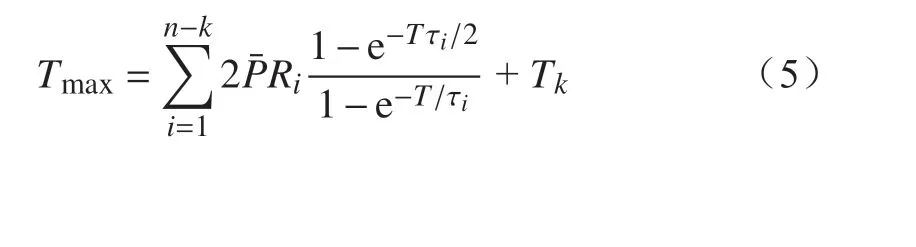
式中:T为恒定高温周期长度; τi为第i级热阻抗网络时间常数;k为热阻抗模型简化的起始级数;Tk为第k级网络的温度。
(4)在温度循环试验中,散热器间歇性通水及不通水。不通水时散热器可近似用一个热容等效。考虑温度循环周期很长,达到分钟级,器件热阻抗网络时间常数为秒级,因此可忽略器件热路的热容并简化为一个总热阻,如图4 所示。
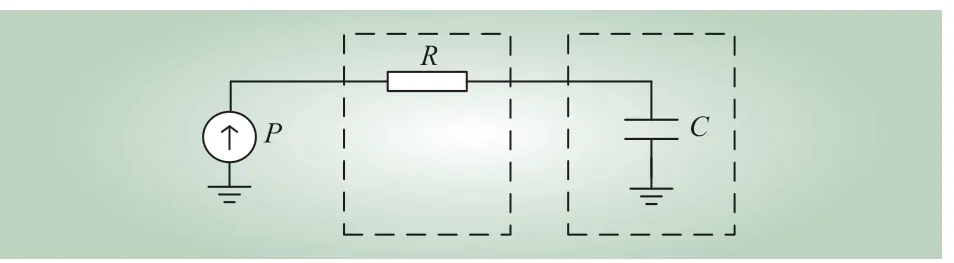
图4 温度循环试验热阻抗网络模型Fig. 4 Thermal impedance model of thermal cycling test
基于上述模型,将温度循环功率等效为方波,即

式中:uc(t)为散热器瞬时温度值;uc(0)为散热器起始温度;Ip为器件损耗;t为温度循环试验周期间隔时间;C为散热器热容。
试验中温度循环试验热损耗波形与正弦波更为接近,可通过半波正弦对热损耗进行等效。
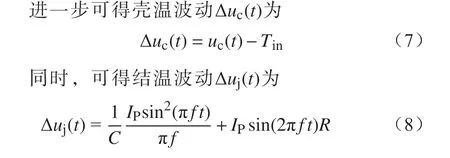
式中:R为模型简化后的热阻;f为电流频率。
温度循环的控制逻辑是被试对象处于升温周期时,停止水冷系统工作,散热器中不通水,结温快速上升。当达到目标结温后被进入冷却周期,水冷系统启动,器件结温与壳温恢复到初始值。
温度循环周期长,器件结温与壳温波动均较大,因此对器件产生很大的热应力和机械应力。温度循环试验负载及器件结温变化如图5 所示。

图5 温度循环试验结果Fig. 5 Results of temperature cycle test
3 试验验证
为满足被试模块结温循环的条件,本文根据老化循环各试验原理搭建了硬件试验平台。测试单元、负载电感、水冷系统对于实验平台来说是主要的负载。供电系统和变压器为试验提供可靠的补能电源系统。试验平台电压输出范围为0~5 kV,电流能力为3 kA,水冷系统功率配置为60 kW。
由于每次试验长达数小时,监测录波数据将占用过多的储存资源,本文采用每次录波60 s 的间隔性录波方法记录老化循环试验过程中负载电流、散热器温度等可量测的数据。测试结果如图6 所示。
根据所提出的功率循环老化方法,调制负载电流对被试功率模块中压接型IGBT 进行循环老化,此过程中散热器水冷进水温为40℃。
温度循环试验中负载电流以及测温点温度波形如图7 所示。通水转折点之前被试模块因负载电流流过且水冷不通水而产生较大的温度波动,从图7 可以看出测温点温度波动达到15℃。温度循环降温阶段加入了通水散热,器件降温转折点很快出现在通水转折点之后,这使得散热器和器件都加速降温,因此该方法可以对压接型IGBT 进行持续地加速老化。
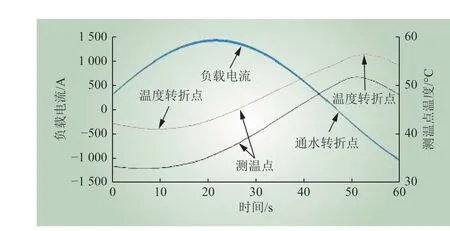
图7 采样曲线Fig. 7 Sampled curve
4 结语
本文提出了加速老化试验方法,其可全面激发压接型IGBT 各部件的疲劳老化,从而全方位地考核器件耐久性与可靠性。本文通过理论计算对各工况下的热路模型进行等效简化,提出了实现不同老化目标的试验条件和整定方法。试验结果显示,在设计的周期性老化循环实验中,各测温点温度均达到了设定目标,为基于压接型IGBT 柔性直流换流阀功率模块的可靠性与耐久性评估提供依据。

