基于锁相环的并网VSC 暂态失稳机理与控制方法
陈征,胡鹏飞,戴立宇,周朝晖,于彦雪,修晓青
(1. 浙江大学 电气工程学院,浙江 杭州 310027;2. 国网福建省电力有限公司电力科学研究院,福建 福州350003;3. 国网福建省电力有限公司,福建 福州 350003;4. 中国电力科学研究院有限公司,北京 100192)
0 引言
近年来,随着双碳目标的不断推进,以风电、太阳能发电为主体的新能源发电技术得到了高速发展。同时,为了应对新能源出力的随机性和波动性,规模化电化学储能系统也将接入电网[1],为新型电力系统提供灵活性和安全性保障。电压源变流器(voltage source converter, VSC)作为新能源和储能设备接入电网的关键电力电子装备,将在新型电力系统中占据更为重要的位置。目前,针对VSC 接入弱电网稳定问题和控制策略已成为研究热点[2]。
常见的VSC 控制方式可以分为组网型控制和跟网型控制,其中,组网型控制适用于弱电网场合,包括电压频率变换(VF)控制、下垂控制、虚拟同步机控制等[3-4],这类控制方式通过直接控制输出电压矢量实现功率调节;跟网型控制适用于强电网场合,其采用锁相环(phase locked loop,PLL)获得电网电压的相位,通过电流矢量控制进行功率传输[5]。为了更好地实现最大功率跟踪,跟网型控制是当前新能源并网的主流控制方式,具有控制简单、响应速度快的特点,但缺乏频率和电压支撑,在弱电网下易发生与PLL 密切相关的失稳问题[6]。
并网VSC 的失稳可以分为小扰动失稳和大扰动失稳,其中,国内外学者对VSC 小扰动失稳现象的研究较为成熟[7]。小扰动稳定性研究的前提是系统存在稳态工作点,主要分析系统在稳态工作点处的阻尼特性,研究发现PLL 控制引起的低频负阻尼是导致VSC 失稳的主要原因[8],而外环直流母线电压控制(DC-bus voltage control, DVC)、内环电流控制等与PLL 之间存在耦合作用,会进一步恶化负阻尼的影响[9]。大扰动失稳主要是分析电网在发生大扰动后,如电网电压跌落、短路故障等,VSC 能否从扰动前的稳态工作点过渡到扰动后的稳态工作点[10]。近些年,随着新能源并网规模的不断增加,大电网的支撑能力逐渐减弱,大扰动对新型电力系统稳定运行的影响愈加复杂[11],因此,国内外学者开始关注VSC 的大扰动(暂态)失稳问题[12-13]。
文献[14]建立了一种准静态PLL 模型来分析VSC 的大扰动稳定条件,并指出PLL 准静态模型中包含的正反馈回路是导致VSC 失稳的原因。文献[15]参照同步发电机模型对PLL 进行了建模分析,并通过加速面积和减速面积研究了VSC 的暂态稳定性。文献[16]研究了PLL 的暂态稳定准则和稳定边界,进而提出了一种通过限制PLL 输出相位来提高暂态稳定性的方法。文献[17]对比研究了一阶和二阶PLL 同步下VSC 的暂态稳定性,并指出只要稳态工作点存在,一阶PLL 同步下的VSC 即不会发生暂态失稳问题。文献[18]建立了带复数滤波器锁相环的并网系统阻抗模型,表明适当的复数滤波器带宽可以改善逆变器在弱电网下的稳定性。文献[19] 针对PLL 同步的弱连接VSC 系统的暂态稳定性,提出了电网对称故障下VSC 有功和无功电流设定值可行域的概念,并分析了短路比、PLL 控制参数等对该可行域的影响。然而,上述研究均忽略了功率外环的影响,文献[20]通过建立涵盖PLL 和DVC 动态的准静态模型研究了VSC 的静态和暂态稳定边界,然而所建模型中由于PLL 和DVC 高度耦合,难以揭示考虑外环影响时VSC 的失稳机理。
综上所述,现有研究多在忽略功率外环影响的前提下,将VSC 的暂态失稳归结为PLL 的同步失稳,研究结果具有一定的局限性[20]。实际上,当电网发生大扰动时,VSC 的暂态稳定性不仅与同步环有关,还与功率环有关。为弥补现有研究的不足,本文以基于PLL 的VSC 为研究对象,考虑功率环的影响,全面研究VSC 并网系统的暂态失稳机理和稳定性提高方法。
(1)以电网电压跌落为例,通过功角特性曲线全面揭示PLL 和功率环的失稳机理,并分别给出其临界失稳电压。
(2)提出一种重新定向d轴的下垂控制方法,有效改善功率环和PLL 同步环的失稳边界。
1 基于PLL 的VSC 暂态失稳机理分析
基于PLL 的VSC 并网系统结构如图1 所示,主要包括主电路、功率外环控制(直接功率控制和DVC 控制)、电流内环控制和PLL。其中:Udc为直流母线电压;Pin为 直流侧输入功率;XF为滤波电感;X为线路阻抗;P和Q分别为VSC注入电网的有功和无功功率;Ug为电网电压;Uabc和Iabc分别为公共耦合点(point of common coupling, PCC)处的电压和电流;Udq和Idq分别为dq轴下的PCC 电压和电流;P*为直接功率控制的给 定 功 率;Ud∗c为DVC 控 制 的 给 定 电 压;Id∗和Iq∗分别为电流内环控制的有功和无功参考电流。由图1 可知,功率外环为电流内环提供有功电流参考,PLL 跟踪PCC 点电压相位,为Park 变换提供所需相位角。由于VSC 在纯感性电网中的暂态稳定性最差[21],本文以纯感性电网为例进行暂态稳定性研究。
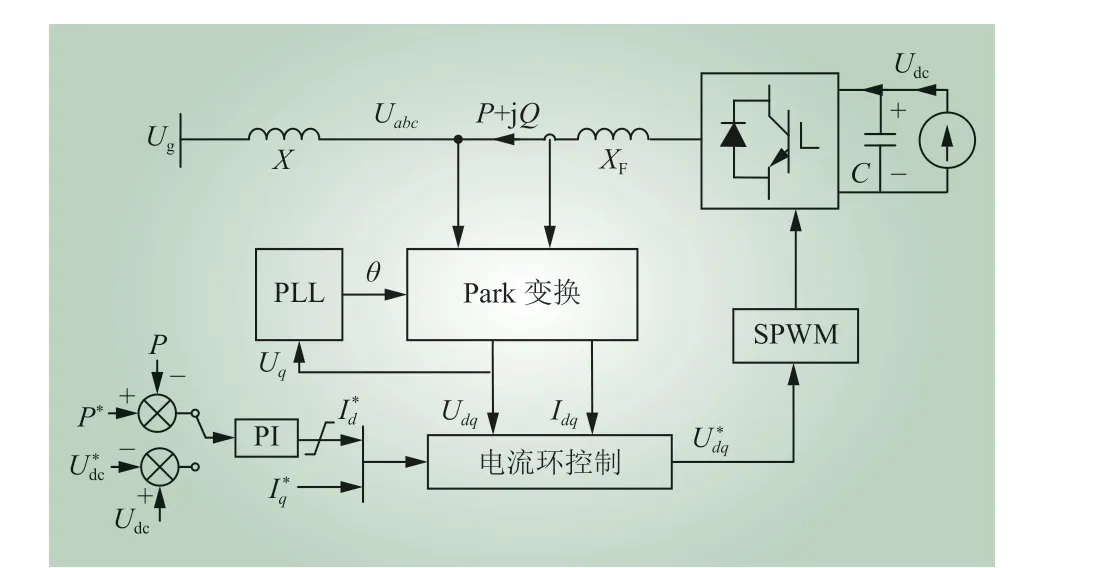
图1 基于PLL 的VSC 并网系统示意Fig. 1 Diagram of PLL-based grid-connected VSC
1.1 PLL 暂态稳定性分析
作为一种跟网控制型逆变器,基于PLL 的VSC 常被等效为一个电流源,其并网等效电路如图2 a)所示,由此可得

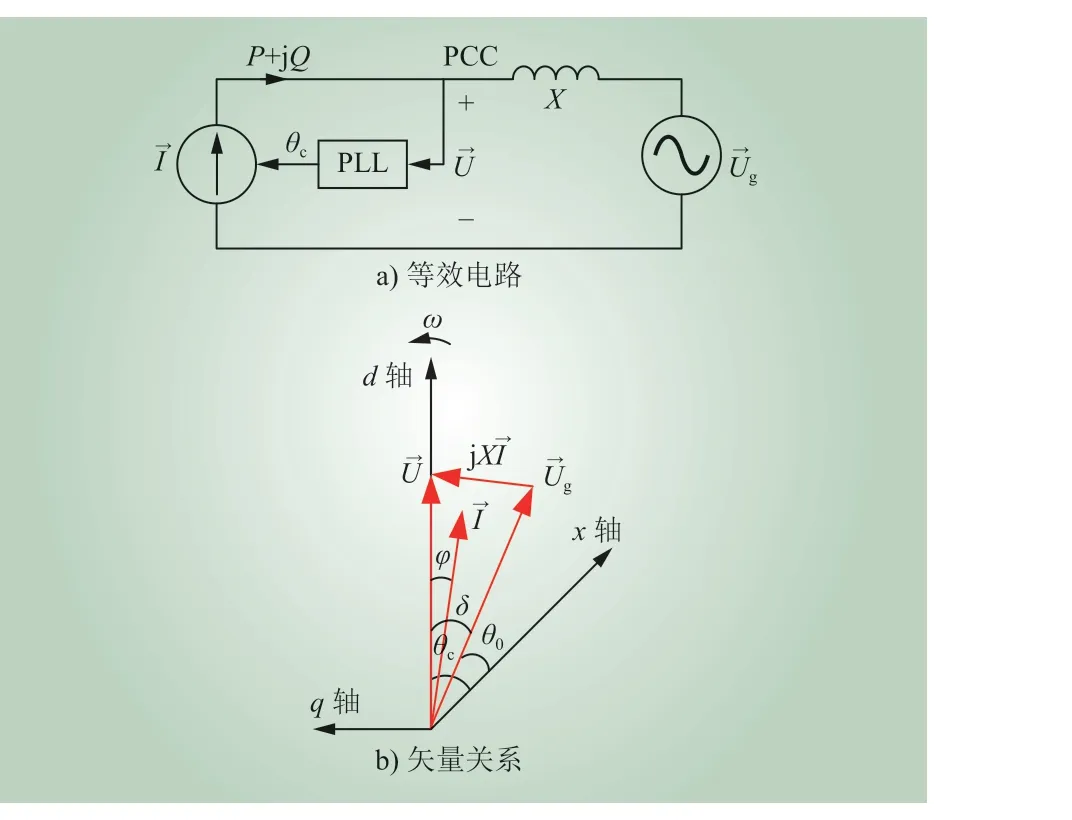
图2 VSC 与电网之间的关系Fig. 2 Relationship between VSC and grid


图3 考虑线路阻抗的PLL 控制框图Fig. 3 PLL control diagram considering line inductance

基于式(4),不同电网电压跌落程度下U-δ之间的关系曲线如图4 所示。由图4 可知,当电网电压跌落较小(即绿色曲线)时,Ugsinδ与XId之间存在交点。此时,只要PLL 控制参数设置合理,电压跌落时系统即可由跌落前的稳态工作点A移动到点G,然后沿着绿色曲线从点G移动到跌落后的稳态工作点C,PLL 维持稳定。然而,当电网电压跌落较大(即红色曲线)时,Ugsinδ与XId之间不存在交点。此时,电压跌落时系统先由工作点A移动到点E,之后工作点逐渐右移直至PLL 失去同步而不稳。因此,保证PLL 暂态稳定的电网电压幅值跌落临界值为XId。
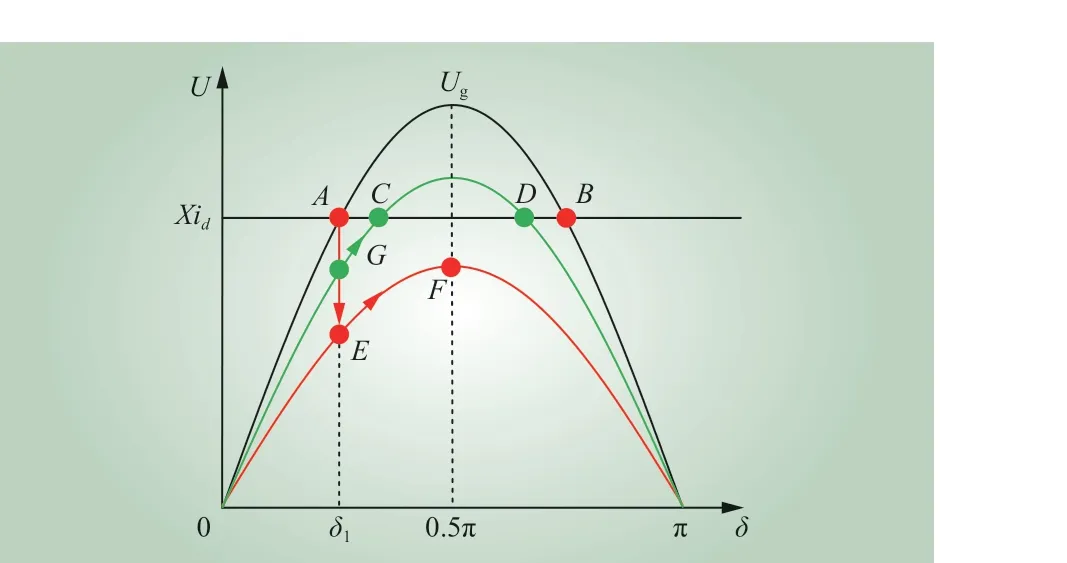
图4 并网VSC 的 U-δ曲 线Fig. 4 U -δ curve of grid-connected VSC
1.2 功率环的暂态稳定性

对图1 所示的2 种外环控制,因为内部电流控制环带宽远高于外环控制带宽,即电流环输出能够很好地跟踪外环的参考输出,所以在分析外环的动态特性时内部电流控制环的影响可以忽略。此时,直接功率控制的反馈信号为有功功率P,基于式(9)可得图5 a)所示的功率闭环控制框图,功率外环控制器通过直接将功率误差控制为0 来实现功率跟踪;DVC 的反馈信号为直流母线电压Udc,根据母线电容功率与Udc的关系,同样可得DVC 外环控制下VSC 的功率闭环控制框图,如图5 b)所示,其中Pin表示直流侧输出功率。DVC 控制器通过将母线电压误差调节为0 来间接实现功率传输。虽然2 种控制的直接控制信号不同,但是系统有功-电流(P-Id)之间的关系均满足式(9),相应的P-Id关系特性曲线如图6 所示。

图5 VSC 的功率闭环控制框图Fig. 5 Closed-loop power control diagram of the VSC
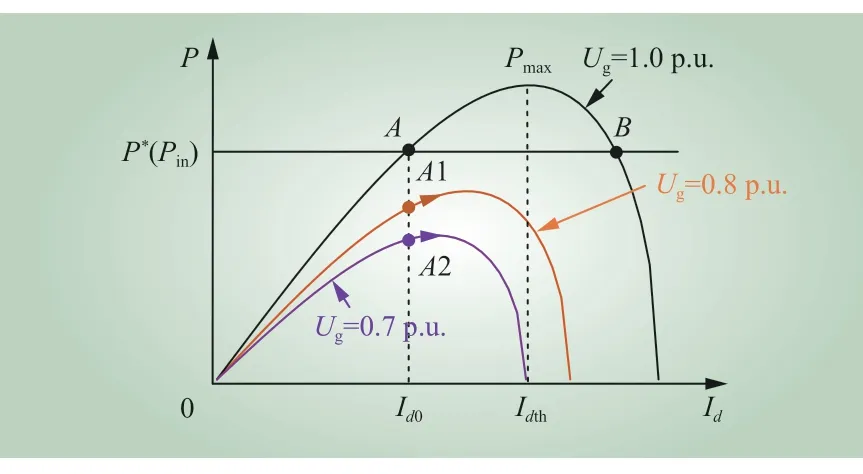
图6 I q=0时 基于PLL 的 并网VSC 的 P-Id曲 线Fig. 6 P -Id curve of PLL-based grid-connected VSC withIq=0



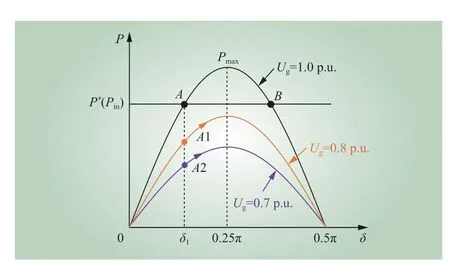
图7 I q=0时 基于PLL 的并网VSC 的 P-δ曲线Fig. 7 P -δ curve of PLL-based grid-connected VSC withIq=0
1.3 VSC 暂态失稳机理分析


2 重新定向d 轴的优化策略

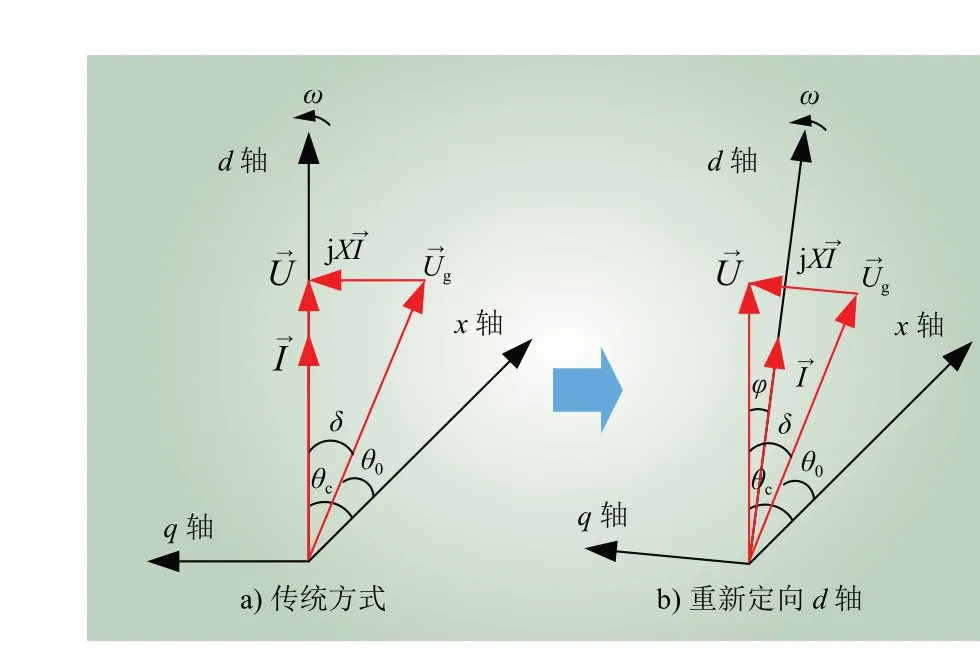
图8 传统方式和重新定向d 轴后PLL 相量图Fig. 8 PLL phasor diagram of conventional and reoriented d-axis methods
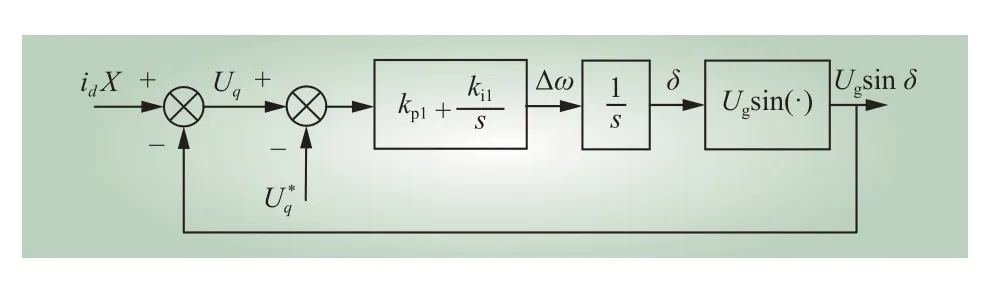
图9 重新定向d 轴后的PLL 控制框图Fig. 9 Re-oriented d-axis based PLL control structure

考虑功率环,在单位功率因数控制下,有功功率表达式为


图10 重新定向d 轴后临界电压曲线Fig. 10 Critical voltage curve with re-oriented d-axis method

3 实验验证
为验证VSC 的暂态失稳机理和暂态稳定性提高方法,在基于RT-BOX 的硬件在环实验平台上进行了实验验证。实验平台如图11 所示,VSC 并网系统参数如表1 所示。其中,PI 控制参数参考典型二阶系统设计。实验中涉及的电压暂降数值均代表电网相电压幅值。

图11 实验设备图片Fig. 11 Photograph of experimental setup
3.1 功率环暂态失稳机理验证
基于式(13),在表1 所示的系统参数下,计算可得功率环发生暂态失稳的临界电压理论值为228.8 V。为了验证理论分析,实验设计中电压暂降深度分别选取临界电压以上(230 V)和临界电压以下(225 V)两种状态。理论上,临界电压以上的系统可以维持稳定,临界电压以下的系统会失去稳定。实验波形如图12 所示。
(1)0~1 s:并网VSC 工作在额定状态,额定参数如表1 所示。
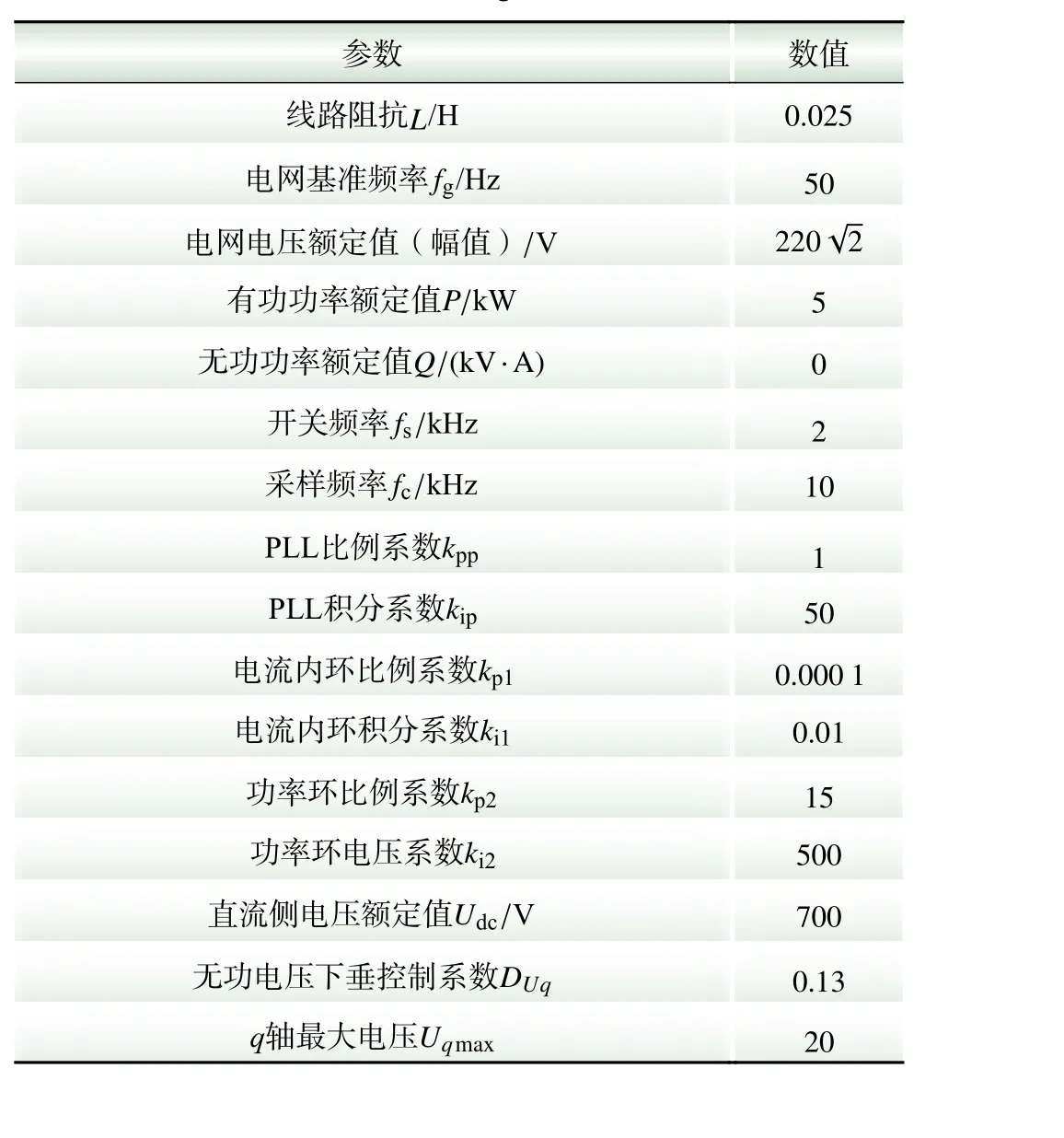
表1 VSC 并网系统参数Table 1 Parameters of grid-connected VSC
(2)1~5 s:在1 s 时,电网电压幅值由额定值跌落到230 V。可以看到,电网电压跌落后后,PCC 点电压很快降低,PCC 点电流缓慢上升,系统在4 s 基本达到稳定。在此时间段,对应的功率波形亦显示,有功功率首先发生暂降,并缓慢恢复到5 kW,系统维持稳定运行。
(3)5~8 s:5 s 时,电网电压从230 V 跌落到225 V。由图12 a)可知,当电网电压降低到225 V 后,PCC 点电压持续下降,PCC 点电流持续增加。图12 b)显示有功功率在5 s 时下降,但是并没有恢复到5 kW。最终系统在7 s 左右失去平衡点。失稳时刻附近的放大波形示于图12 a)对应波形的上方。
比较图12 所示的两阶段电网电压跌落实验可知,电网电压下降后,PCC 电流会增加,而PCC 电压会降低。不同之处在于,当电网电压降至230 V 时,系统可以保持稳定,但当电网电压降至225 V 时,系统无法达到新的稳定状态。证明功率环失稳的临界电压为225~230 V,与理论分析值228.83 V 基本一致。
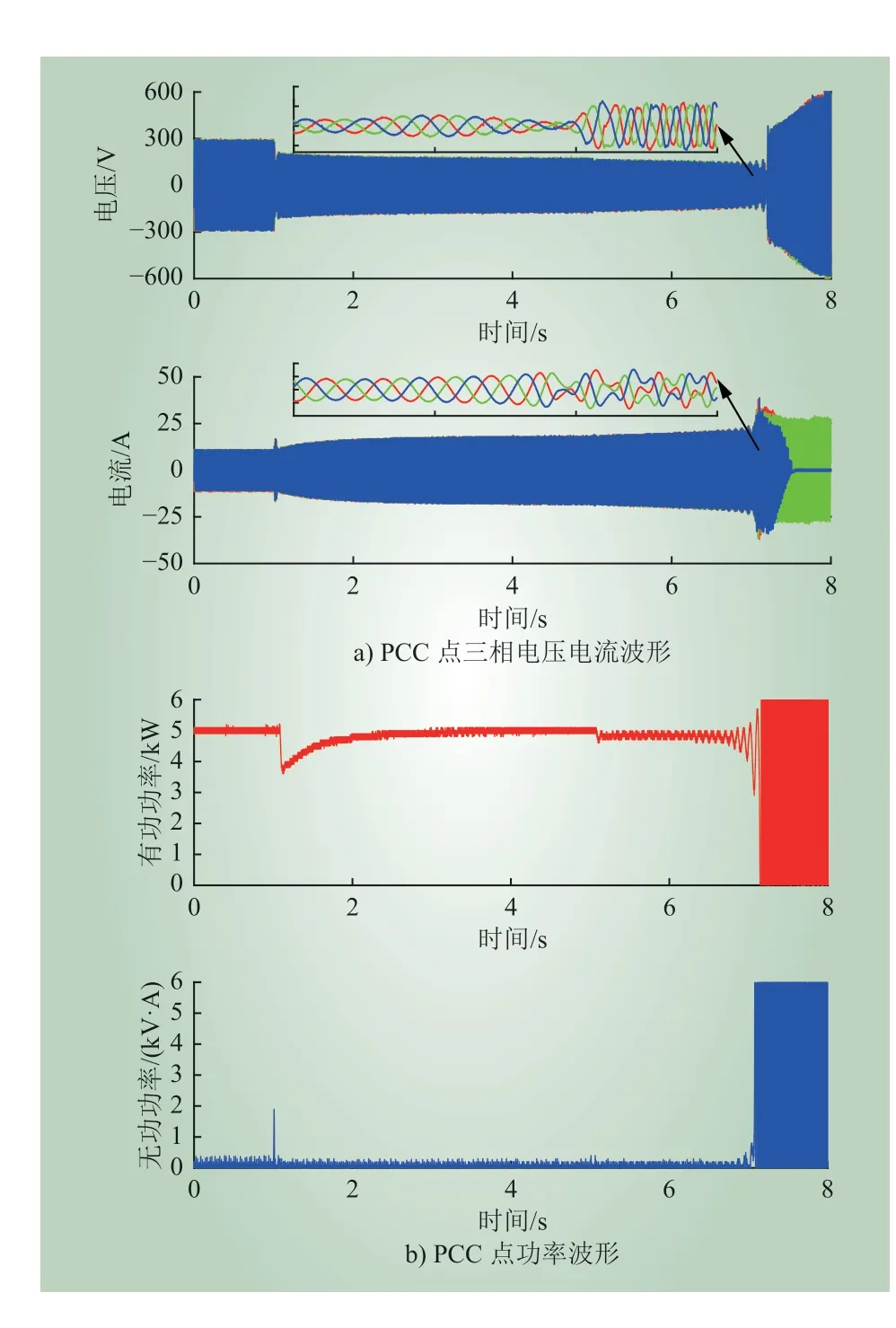
图12 考虑功率环时VSC 的电网电压暂降实验波形Fig. 12 Experimental waveform of the VSC with power loop under voltage sag
图13 所示为无功率环控制VSC 在电网电压发生跌落时的实验波形,其中Id=20.6 A(与图12 所示功率控制环存在时VSC 的并网电流额定值保证一致)。图13 中仅展示了A 相电压和三相电流波形。
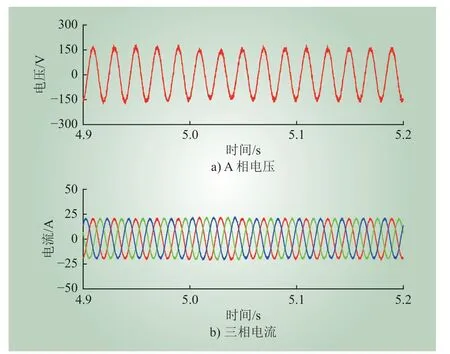
图13 无功率环时VSC 的电网电压暂降实验波形IFig. 13 Experimental waveform I of the VSC without power loop under voltage sag
(1)4.9~5.0 s:电网电压为230 V,此时PCC 点理论测量电压为163.5 V,系统稳定运行。
(2)5.0~5.2 s:5.0 s 时,电网电压从230 V 降至225 V,此时PCC 点理论测量电压为156.4 V,并网电流发生轻微波动并快速达到新的稳定运行点。
由此表明,在功率环失稳条件下,PLL 没有失去同步稳定。
3.2 PLL 暂态失稳机理验证
为验证PLL 的暂态失稳机理,实验中的VSC控制环路仅保留PLL 和电流内环,其电流内环的给定电流分别为Id=20.6 A、Iq=0 A。在表1 所示的系统参数下,由式(5)计算可知,PLL 的临界失稳电压为161.8 V。实验设计与功率环类似,在此不再赘述。实验波形如图14 所示。
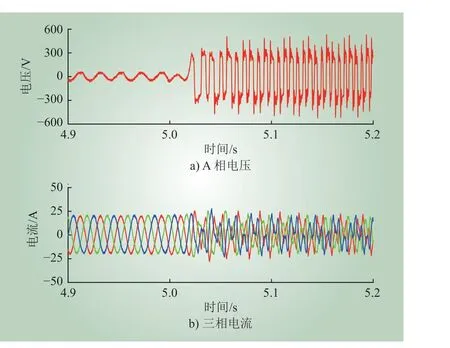
图14 无功率环时VSC 的电网电压暂降实验波形IIFig. 14 Experimental waveform II of the VSC without power loop under voltage sag
(1)4.9~5 s:电网电压为170 V,PCC 点理论测量电压为52.2 V,系统稳定运行。
(2)5.0~5.2 s:5 s 时,电网电压由170 V 降至160 V,系统很快失稳。
由此可得,PLL 失稳电压在170 V 与160 V 之间,验证了理论分析的准确性。
3.3 重新定向d 轴控制方法验证
为了提高VSC 的暂态稳定性,进一步降低VSC 运行的临界电压值,引入重新定向d轴的控制方法。图15 所示为对应的实验波形。
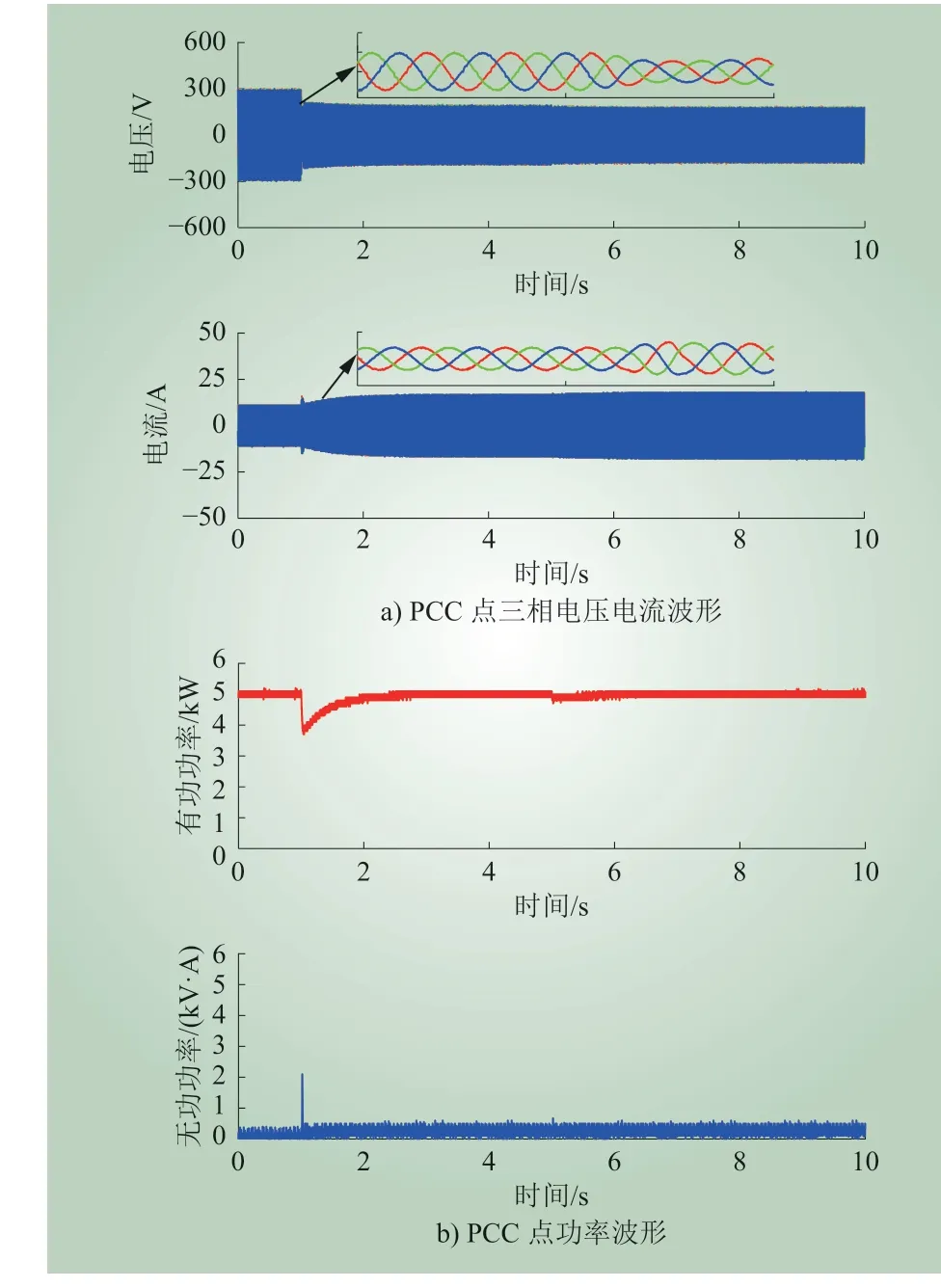
图15 重定向d 轴控制下VSC 的电网电压暂降实验波形Fig. 15 Experimental waveform of the VSC with reorient d-axis control under voltage sag
(1)0~1 s:系统运行在额定状态。根据采集到的PCC 点电压、电流和功率波形可见,此时,无功功率基本为0,不影响额定状态下VSC 的并网功率因数。
(2)1~5 s:1 s 时,电网电压幅值跌落至230 V。由图15 可知,PCC 处的电压降低,电流略微增加。因PCC 电压下降,重新定向d轴控制开始起作用并向系统注入无功功率,无功波形高于0。
(3)5~10 s:5 s 时,电网电压幅值从230 V继续降至225 V,无功注入继续增加,经过短暂调节后系统达到新的稳定状态。对比图12 所示的实验结果,可以证明本文所提暂态稳定性提高方法的有效性。
4 结论
本文以电网电压跌落故障为例,考虑功率外环的影响,全面研究了基于PLL 的VSC 并网系统的暂态失稳机理和暂态稳定性提高方法。经仿真验证取得以下结论。
(1)系统失稳的本质原因是功率环失稳,只有当功率外环不存在时,系统失稳才可归结为PLL 失去与电网的同步;

(3)重新定向d轴自适应无功控制方法,可同时改善功率环和PLL 的稳定运行边界,并可根据电网电压跌落深度实现无功注入的自适应调节,有效提高了VSC 的暂态稳定性。

