博弈论赋权和灰云模型的建筑地基稳定性评价

黄金波 王轶多

(浙江省建工集团有限责任公司, 浙江 杭州 310012)

0 引言

随着城市化进程的不断推进,建筑业也不断发展,并不断尝试在采空区上方进行建设[1]。但采空区存在地表变形,会威胁建筑物的安全。因此,为了采空区建筑的安全使用,对采空区建筑地基进行稳定性评价显得尤为主要[2]。

长期以来,许多专家学者对采空区建筑地基的稳定性进行了研究。其中,刘洋等[3]利用层次分析法和模糊评价理论对采空区建筑地基稳定性进行综合评价,所得评价结果与实际矿山情况相吻合；赵超等[4]将层次分析法与可拓评价理论法相结合,建立了建筑地基稳定性评价的物元模型,准确地判别出稳定性等级,其稳定性评价结果对于采空区的治理提供了科学、有效的依据。上述研究虽然取得了一定的成果,但对采空区建筑地基进行稳定性评价是一个复杂的过程[5],仅采用单一赋权方法具有一定的主客观性,降低评估结果的可靠性[6]。

为此,本文先结合已有研究构建了建筑地基稳定性评价指标体系,并基于层次分析法、改进的标准间重要性相关性(criteria importance though intercrieria correlation,CRITIC)法对评价指标进行主客观赋权,最后再采用灰云模型理论,建立了一套建筑地基稳定性评价模型,避免了专家主观决策对评价结果的影响,从而获得了科学、准确的建筑地基稳定性评价结果。

1 评价指标体系的构建

由于影响采空区上方建筑地基稳定性的指标众多,且部分指标存在一定的冗余性,为了对建筑地基合理地进行稳定性评价,通过综合考虑采空区的实际情况以及参考相关文献,选取出涵盖停采时间、深厚比等7个指标构建了稳定性评价指标体系,如图1所示[7-8]。将采空区建筑地基稳定性划分为Ⅰ、Ⅱ、Ⅲ和Ⅳ级,分别代表稳定、基本稳定、欠稳定和不稳定,各评价指标分级标准如表1所示[9]。

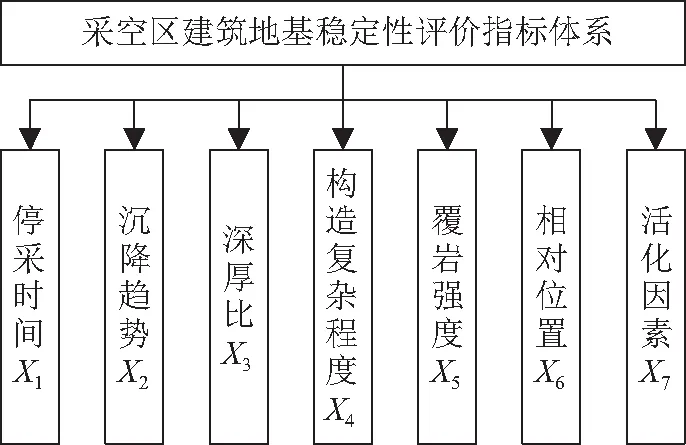
图1 采空区建筑地基稳定性评价指标体系

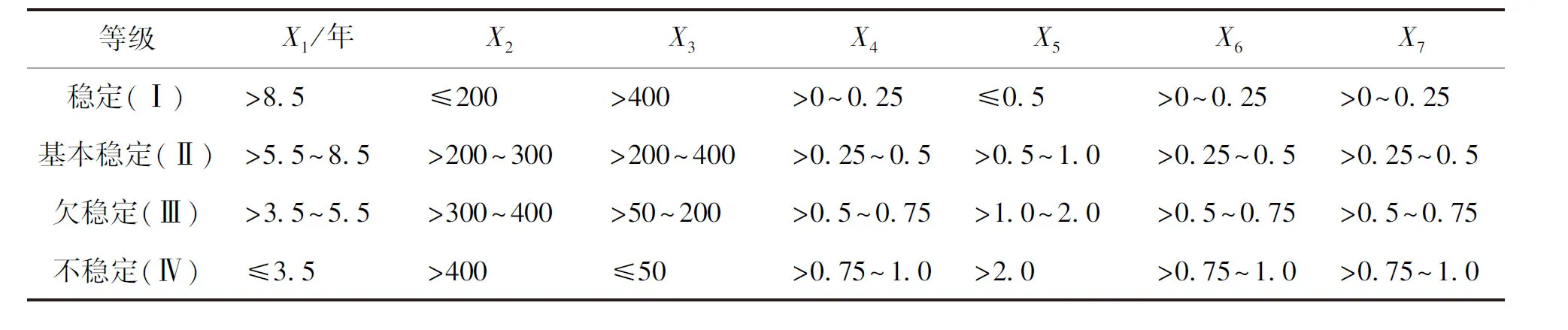
表1 评价指标分级表

2 评价指标的组合赋权

2.1 层次分析法确定主观权重

在本文中,以层次分析法对评价指标进行主观赋权,依据1～9标度表[10]对评价指标进行两两比较,确定评价指标的相对重要性,从而构建判断矩阵F,如式(1)所示[11]。

(1)

式中,flt为指标l与指标t的比值；n为指标个数。

根据矩阵F计算最大特征根λmax相对应的特征向量,并对向量进行归一化处理,得到各评价指标的权重P,实现对评价指标的主观赋权。为保证所得权重的合理性,必须对矩阵进行一致性检验。一致性比例CR可定义为

式中,CI为一致性指标；RI为平均随机一致性指标。

RI随着评价指标数量n的变化而变化,其具体取值如表2所示。当一致性比例CR<0.1时,认为判断矩阵F具有良好的一致性,若CR>0.1则需对判断矩阵F进行适当调整,直至其满足一致性。

表2 平均随机一致性指标RI

2.2 改进的CRITIC确定客观权重

CRITIC不仅考虑了指标之间的信息量,而且顾及了指标之间的相关性。但是,不同指标间的量纲、数量级往往不同,CRITIC法用标准差衡量指标的变异性存在一定的不足[12]。因此,采用变异系数对CRITIC法进行改进,更好地实现指标赋权,其主要步骤如下[13]:

(1)以原始评价指标值构建矩阵X,如式(4)所示。

(4)

式中,xij为第i个评价对象第j个评价指标值；m为评价对象数目；n为评价指标数目。

(2)对矩阵X中的元素进行标准化处理,得到标准化矩阵X*=(xij*),标准化计算如式(5)所示。

(5)

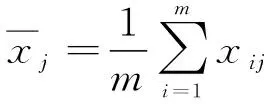
(3)计算指标体系中各指标的变异系数vj,如式(6)所示。

(6)

(4)通过SPSS软件,可计算出矩阵X*中各指标的Pearson相关系数,并构造出相关系数矩阵R=(rkj)n×n(k=1,2,…,n;j=1,2,…,n),再根据式(7)计算各指标的独立性系数ηj。

(7)

(5)结合所求的变异系数和独立性系数,由式(8)计算各指标的重要性系数Hj。

(8)

最终可通过式(9)计算第j个评价指标的权重Qj。

(9)

2.3 博弈论组合赋权

基于博弈论的综合赋权法,将由层次分析法确定的主观权重与由改进的CRITIC确定的客观权重相结合,从而得到评价指标的综合权重[14]。具体算法如下:

对于多指标评价系统,假设采用L种方法得到指标的权重,即权重向量W为

(10)

以此得到一个权重集W,L种权重向量的线性组合如式(11)表示。

(11)

式中,αk为线性组合系数,αk>0；W为所有的权重向量集。

为了选择出最合适的权重向量W*,需对线性组合系数进行优化,使得W与每个wk的离差极小化,并导出其目标函数。

(12)

按照矩阵微分性质,与上式等价的最优一阶导数条件为

(13)

对式(14)进行求解可得(α1,α2,…,αL),然后通过式(15)对其进行归一化处理,即可得到综合权重向量W*。

3 灰云模型理论

灰色模型是在云模型理论的基础上引进灰色理论,解决了模糊概念的定量化处理,从而实现定性与定量之间的转换[15]。灰云模型采用指标分级的上下边界(Tx,Px)、峰值Rx、熵En和超熵He等数字特征进行转换。不同稳定性等级所对应的灰云模型数字特征的计算方法如表3所示,其中k为常数,其可以调节云模型云化程度,通常取值为7[16]。

表3 灰云模型数字特征

根据表3可确定出灰云模型的数字特征,采用MATLAB软件可生成评价指标的灰云模型,再结合博弈论所得的组合权重,基于最大隶属度原则便可得到各评价对象所隶属于各稳定性等级的确定度。

4 工程实例

本文以徐州夹河煤矿与庞庄煤矿的井田为例[17],运用所构建的采空区建筑地基稳定性评价体系以及模型,对该研究区域进行稳定性评价。

4.1 评价指标权重的确定

首先利用层次分析法,对7个评价指标进行两两比较,所构造的判断矩阵为

(16)

层次分析法确定的权重如表4所示。根据判断矩阵F计算得到的特征值λmax=7.249 4和一致性比例CR=0.030 6<0.1,判断矩阵满足一致性,所得的权重有效。

再根据改进的CRITIC方法计算评价指标权重,结果如表4所示。根据博弈论的组合原则,得到各评价指标的组合权重,如表4所示。

表4 评价指标权重

4.2 判定稳定性等级

根据灰云模型理论,编写MATLAB程序求解各建筑地基隶属于各稳定等级的确定度,并基于最大隶属度原则确定出各建筑地基的稳定性等级,结果如表5所示。

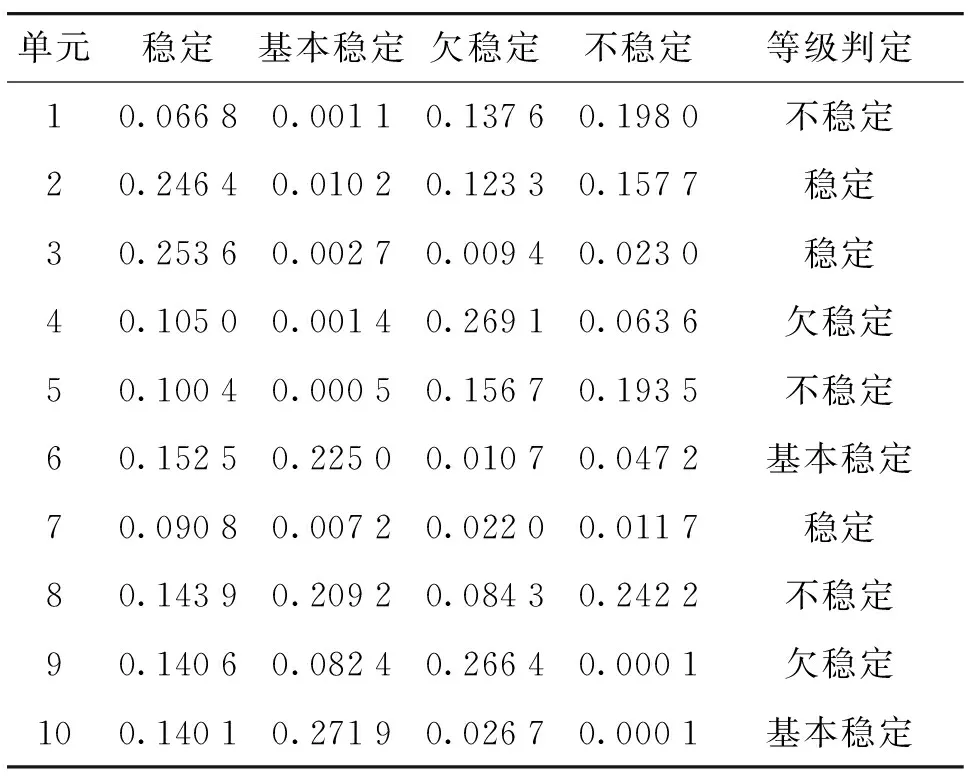
表5 建筑地基稳定性等级判定

5 结束语

基于组合赋权法和灰云模型理论构建了建筑地基稳定性评价模型,并将其应用于具体工程实例中,其主要结论如下:

(1)采用层次分析法和改进的CRITIC法分别确定评价指标的主客观权重,能有效减小单一赋权造成的误差,消除指标之间的差异性,提高评判结果的可靠性。

(2)采用灰云模型理论构建地基稳定性评价模型,实现定性指标与定量数据的转换,从而得到各地基的稳定性等级,综合反映了地基稳定性评判过程中的灰性和随机性,为采空区建筑地基稳定性的评价提供了一种新方法。