换流阀触发光纤故障分析与电场仿真

杨知非， 董曼玲， 杜君莉， 郭培， 王栋

(国网河南省电力公司电力科学研究院， 郑州 450052)

直流输电技术相对于交流而言，具有长距离输电能量损耗低、输电线路稳定性好等优点，适合于中国资源分布不均而导致的长距离输电限制问题[1-4]。换流阀作为直流输电的核心设备，起着整流、逆变、开关等关键作用[5-8]。文献[5]针对特高压换流阀状态评估中原始数据不均衡、模型难以解释等问题，提出一种基于轻量梯度提升机与Shap归因分析的特高压换流阀状态评估方法。文献[6]针对换流阀模块的倒角剖分问题，采用了适合大规模问题求解的多极子加速曲面边界元法，分析了不同倒角下拐角处电场的变化情况。文献[7]采用计算流体动力学数值模拟方法，合理设计了换流阀冷却系统中离子交换器的规格和内部结构。文献[8]为解决现有换相失败预防控制在某些故障情况下启动不及时的问题,通过引入换相电流时间面积判据，提出了一种启动更加迅速的换相失败预防控制改进策略。

光直接触发晶闸管是伴随电子技术而出现的一个关键，采用光触发后，系统的稳定性逐步提高，电路结构得到简化，故障出现的概率大大减小，系统的可靠性有了一个全新的进步[9]。

目前，国内外学者针对阀厅内部的电场仿真做了大量的研究。文献[10]以±1 100 kV直流换流阀模块内部金属部件和层间绝缘子为研究对象，采用SolidWorks及Ansys 混合建模技术，建立了研究对象的三维模型。对该模型进行了单阀直流耐压试验仿真和交流耐压试验仿真，得到其电场分布结果，根据此结果对模型进行了绝缘优化。文献[11]根据±800 kV多端柔直换流站直流场的设计方案和设备布置，建立了三维全场域有限元仿真模型，计算分析了运行工况下直流场中各均压屏蔽装置的电位、电场分布，基于控制场强提出了典型金具的差异化优化思路与改进方向。然而，很少有学者对晶闸管触发光纤的电场分布进行研究。现将以现场故障为实例，对晶闸管触发光纤进行电场仿真，同时考虑了光纤材料电阻率改变对电场畸变的影响以及光纤电位未被钳制情况下对电场分布的影响，有效分析了光纤故障点处局部放电的原因。

1 换流阀结构

某±120 kV换流站换流阀为光触发换流阀。该换流阀每相阀塔共4层，包括4个单阀，每个单阀含2个阀段，每个阀段含11个晶闸管级(3根触发光纤、11根回报光纤、2根反向恢复保护光纤、1根触发回检光纤)；每个晶闸管级包括1个晶闸管、1个晶闸管电压监测(thyristor voltage monitoring, TVM)板、1根回报光纤，如图1所示。

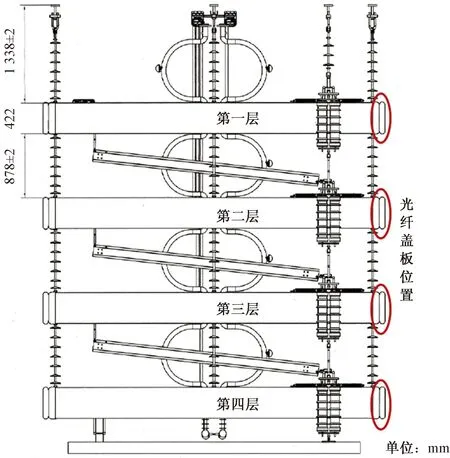
图1 阀体光纤盖板位置Fig.1 Position of optical fiber cover plate

每个单阀触发、回报光纤使用波纹管单独包裹成束后，逐层向上汇集，并在波纹管外部包裹一层防火布，光纤束在每层阀屏蔽罩处使用光纤盖板固定(每个盖板固定的光纤数量一致)，并通过盖板中的泡沫塑料(材质PE 45 EVA，半导体材料，具有钳制电位作用)实现等电位，如图2所示。

2021年7月，换流阀C相第四层晶闸管634、635故障，单阀晶闸管失去冗余，手动切换系统后故障仍然存在。

报文中634、635编码分别对应换流阀C相第四层单阀V14、V15晶闸管级，现场开展C相阀塔外观检查，重点检查V14和V15晶闸管、TVM板、阻尼电容及电容托架等，均未见异常，阀控VBE系统无告警，如图3、图4所示。

现场对C相第四层单阀全部22个晶闸管级进行晶闸管阻抗及触发试验，均正常，并对该阀段晶闸管级进行均压试验，各晶闸管级间电压分布均匀，判断此单阀晶闸管、阻尼回路、多模星型耦合器(multi-mode star couple,MSC)光分配器、MSC光分配器至晶闸管门极触发光纤均正常。

图2 光纤结构图Fig.2 Optical fiber structure diagram

图3 VBE屏柜无告警Fig.3 VBE cabinet no warning

图4 C相Y桥阀5组件外观检查Fig.4 Visual inspection for phase C Y-bridge valve 5 assembly

现场对V14、V15晶闸管级外施交流电压，在VBE阀基电子设备侧无光信号反馈。检查C相第四层单阀内所有回报光纤衰耗，仅发现V14、V15晶闸管回报光纤异常。

为检查光纤故障位置，将C相阀塔光纤盖板全部打开，发现第三层单阀的盖板内V14、V15晶闸管回报光纤表皮存在表皮脱落现象，如图5所示。对其他单阀光纤盖板全部打开检查，未发现明显异常(三相阀塔内共计30个盖板)。

图5 第三层屏蔽罩盖板内回报光纤表皮脱落Fig.5 The skin of the optical fiber in the cover plate of the third layer shield falls off

2 光纤样品形貌分析

针对此故障，现场截取了外皮破损的回报光纤，及对应光纤盖板处黑色泡沫塑料，开展上述样品的宏观及微观形貌分析。

2.1 宏观形貌分析

通过宏观观察，发现故障点处回报光纤整体体积膨大，且沿长度方向直径明显缩小。针对故障点回报光纤体积膨大情况，沿长度方向解剖，对内部光纤进行目视检查。图6所示为解剖后裸露的内部光纤形貌图，可以看出内部光纤在同样位置存在体积膨大，直径随长度方向显著缩小，光纤出现拉丝现象，说明故障点处光纤整体出现熔融现象。

2.2 微观形貌分析

针对故障点处回报光纤外皮烧蚀情况，利用扫描电镜开展了微观形貌分析，得到图7所示故障点处回报光纤典型区域微观形貌图，从图7(a)和图7(b)可看出，故障点处前端直径逐渐变细，前端有凹坑，说明外皮熔融程度较高，出现软化和流动现象。

图7(c)所示为故障点回报光纤体积膨大处表面微观形貌图，可看出表面存在熔融区域和烧蚀坑，对熔融区域[图7(d)、图7(e)]和烧蚀坑[图7(f)]进行微观形貌分析，可以看出熔融区域表面已烧蚀完全，烧蚀坑部分区域未烧蚀完全，说明故障点光纤熔融程度沿长度方向减弱。针对破损处位置黑色半导体材料部分烧损情况，进一步截取表面烧损部位和下部正常状态部位，利用扫描电镜开展烧损前后半导体材料形貌对比分析。

图8所示为烧损前后破损处位置的黑色半导体材料微观形貌图。从图8(a)图中可看出，正常黑色半导体材料多孔结构，孔壁薄，相互连接。在烧损后，如图8(b)所示，多孔结构塌陷，孔壁交联在一起，表面聚集大量颗粒物，说明破损处光纤盖板位置黑色半导体材料表面烧蚀严重。

综上所述，故障点处光纤是由局放放电而导致的烧蚀。下文将针对触发光纤进行电场仿真，以此来分析发生局部放电的原因。

图6 解剖后裸露的内部光纤形貌图Fig.6 Morphology of bare optical fiber after dissection

图7 故障点处回报光纤微观形貌图Fig.7 Micrograph of optical fiber at fault point

图8 破损处塑料泡沫材料烧损前后微观形貌Fig.8 Microstructure of plastic foam before and after damage

3 光纤样品仿真计算

3.1 数学模型

3.1.1 有限元法介绍

在数值计算方法中，有限元法应用非常广泛。其优势在于灵活性，极适宜于具有复杂边界条件的数学物理方程问题。特别当计算区域的结构十分复杂时，应用有限元法显得更为方便灵巧。文献[12]以220 kV油纸电容式套管为研究对象，利用有限元法对套管温度场进行了计算。文献[13]以输电线路复合绝缘子为研究对象，通过建立起伞裙完整状态、不同破损位置及程度状态时的有限元电场仿真模型，对比分析了前后状态的电场分布特征。

电磁场的计算问题即是一个求解位场边值问题。若给定二位边值问题[14]为

(1)

式(1)中：ε为介电常数；φ为电位；f为一已知函数；n为平面的法向量。

则其等价于下属问题的求解，即

(2)

式(2)中：J、W为能量函数。

有限元方法即从求解能量极值函数入手，可以看出能量函数J(φ)，对应于不同的电位函数φ(它们都应满足同一边界条件)就有不同的积分值，所以它是一个以函数作变量的函数，称为泛函数，简称为泛函。上述等价问题称之为边值问题的等价变分问题。也就是说，边值问题的解函数，可以通过求解变分问题(泛函的极值函数)来获得。

3.1.2 电场控制方程

场计算模型包含控制方程(麦克斯韦方程组)、本构关系及边界条件等三要素[14]，本文换流阀及光纤模型主要承受直流电压，可以按照直流电场来分析。

其控制方程为

∇·J=0

(3)

∇·E=0

(4)

式中：J为电流密度矢量，A/m2；E为电场强度，V/m。

场量与媒质特性关系(本构方程)式为

J=γE

(5)

式(5)中：γ为媒质的电导率，S/m。

场强E可以表示为电位φ的梯度，即

E=-∇φ

(6)

导出方程

∇2φ=0

(7)

式(7)中：∇2为拉普拉斯算子。电位φ的拉普拉斯方程为

(8)

电磁场理论中，电场具有三类边界条件：

第一类为狄里赫希边界条件，即给定边界上的电位值为

φ|Γ1=φ

(9)

式(9)中：Γ为模型边界。

第二类为诺以曼边界条件，即给定电位的法向导数：

(10)

式(10)中：r、z为柱坐标下的表示。

第三类边界条件为混合边界条件，即第一类与第二类边界条件的线性组合。

3.2 仿真建模

为了便于计算，在不影响计算精度的情况下适当的简化模型，以第3层屏蔽罩为研究对象，建立第2、3、4层屏蔽罩模型、光纤模型、卡扣盖板及底座模型，仿真模型整体及重点部位如图9所示。

图9 光纤仿真模型图Fig.9 Optical fiber simulation model diagram

建模时，屏蔽罩尺寸、盖板及底座尺寸参数均严格按照设计图纸和现场实测值设置。由于单根光纤的尺寸过细，在大尺度建模分析中很难做到单根超细光纤的建模及剖分处理，故本模型中将34根光纤视为1整束光纤进行等效建模，尺寸按照波纹管尺寸设置。

3.3 材料参数赋值

屏蔽罩在运行中主要承受的为直流电压，因此其电场分布与材料电阻率直接相关，故在本模型中，各种材料电阻率设置如表1所示。其中光纤、防火棉及半导体材料的电阻率按照现场实测取值，空气电阻率按理想绝缘气体取值。

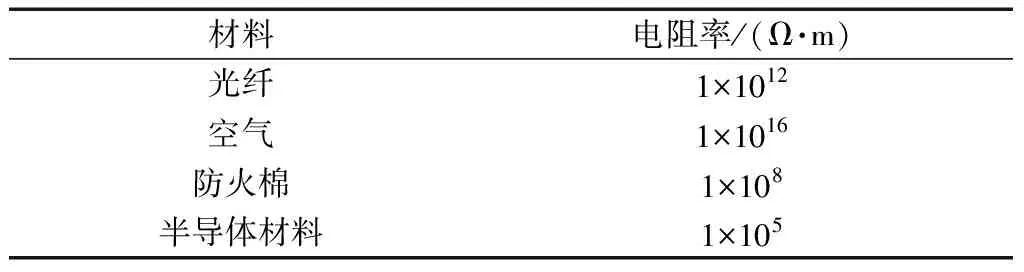
表1 材料参数Table 1 Material parameters

3.4 网格剖分

由于光纤固定架及光纤相对于整体模型体积较小，为了保证网格形状的完好性以及计算模型的准确性，在网格剖分之前，需添加网格控制框，如图10所示。同时，仿真结果分析主要在3号屏蔽罩附近，需在此增加屏蔽罩网格控制框，如图11所示。

为了加载边界条件(0电位)，在整体模型的无穷远处建立整体0电位点，根据电场计算经验，一般建立整体模型3～5倍尺寸的边界条件控制框即可保证计算结果的准确性如图12所示。

整体模型及网格控制框建立之后即可对模型进行剖分，剖分遵循由内到外、有密到疏的原则。

光纤固定架及防火棉、半导体、固定架网格控制框的剖分如图13所示，网格尺寸为10 mm，网格量为120 891。屏蔽罩的网格剖分：由于每个屏蔽罩为等电位，且为不太关注的区域，因此不需要大量的网格剖分屏蔽罩，在此设置网格尺寸为10 cm，如图14所示，网格量为33 267。

依照由内到外、由密到疏的原则，进行网格控制框的剖分，网格剖分结束后，总网格量为1 921 490，其中光纤网格占比为65.4%，光纤网格数过半，保证了光纤电场计算的准确度。

图10 光纤固定架及光纤网格控制框Fig.10 Optical fiber holder and optical fiber grid control frame

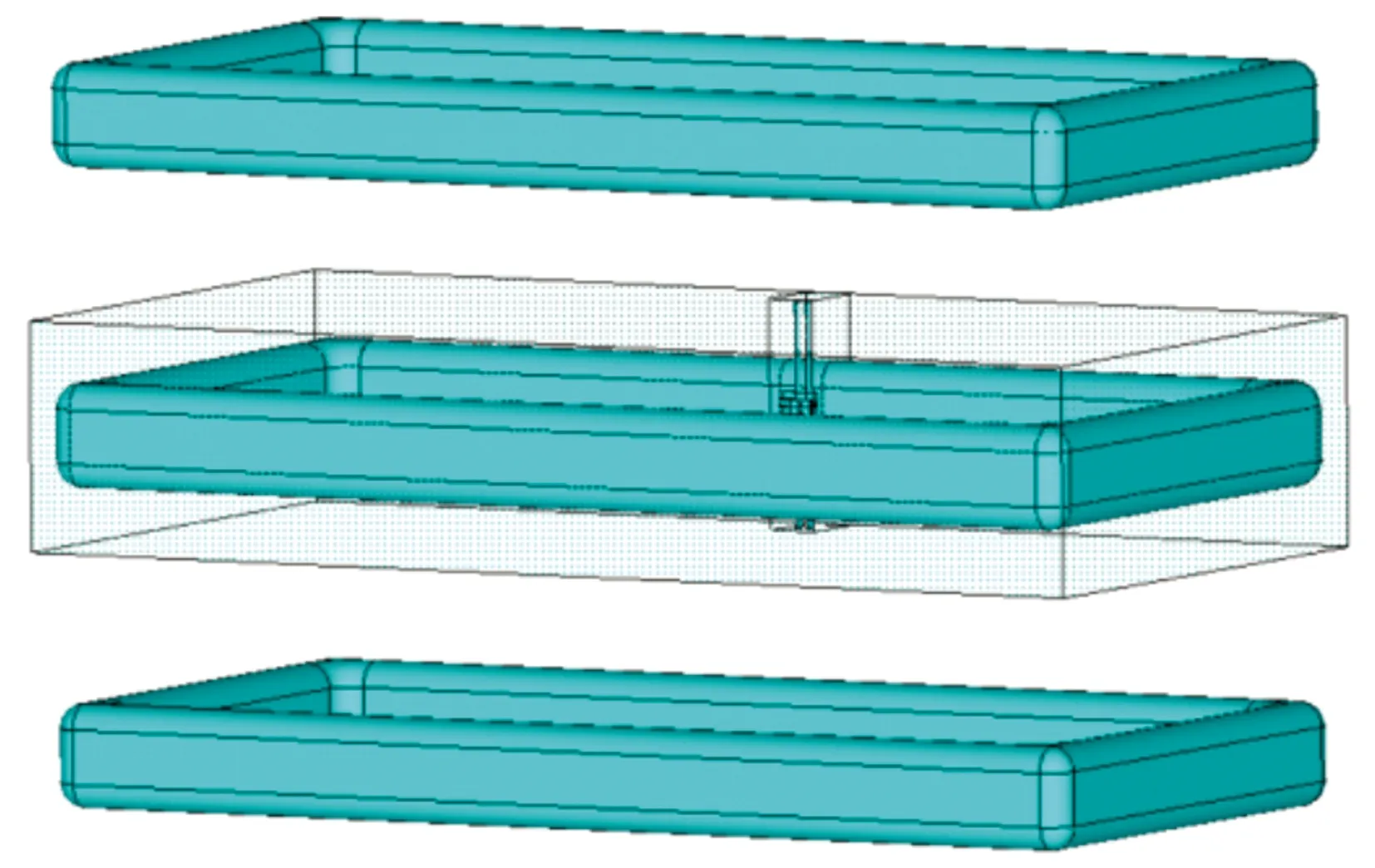
图11 屏蔽罩网格控制框Fig.11 Shield grid control frame

图12 边界条件控制框Fig.12 Boundary condition control frame

图13 光纤固定架及防火棉、半导体、固定架网格控制框的剖分Fig.13 Meshing of optical fiber holder, fireproof cotton, semiconductor and grid control frame

图14 屏蔽罩的剖分Fig.14 Meshing of shield

3.5 电位加载

换流阀上整体电位为120 kV，每个屏蔽罩之间的电压为40 kV。遵循电场计算中电位加载原则，以及实际运行工况，电位加载如下。

(1)在第2层屏蔽罩上加载40 kV电压；

(2)在第3层屏蔽罩上加载80 kV电压；

(3)在第4层屏蔽罩上加载120 kV电压；

(4)在边界条件控制框上加载0电位；

(5)将光纤固定架与第3层屏蔽罩电位进行耦合。

4 仿真结果分析

4.1 理想结构情况下的电场分析

在下述理想结构条件下开展电场仿真分析。

(1)每层阀塔的光纤排列整齐紧凑，光纤之间无间隙。

(2)每根光纤电阻率分布一致，且设为1×1 012 Ω·m。

(3)光纤与盖板及其底座接触良好，即光纤电位被钳制。

阀塔整体电位分布如图15所示，可以看出，电位分布主要集中在三个屏蔽罩之间，可视为三个平板电容器。

3号屏蔽罩附近及盖板附近光纤电位分布如图16所示，可以看出，3号屏蔽罩、光纤盖板及其底座的电位相同均为80 kV，整体上光纤电位自上而下均匀递增。

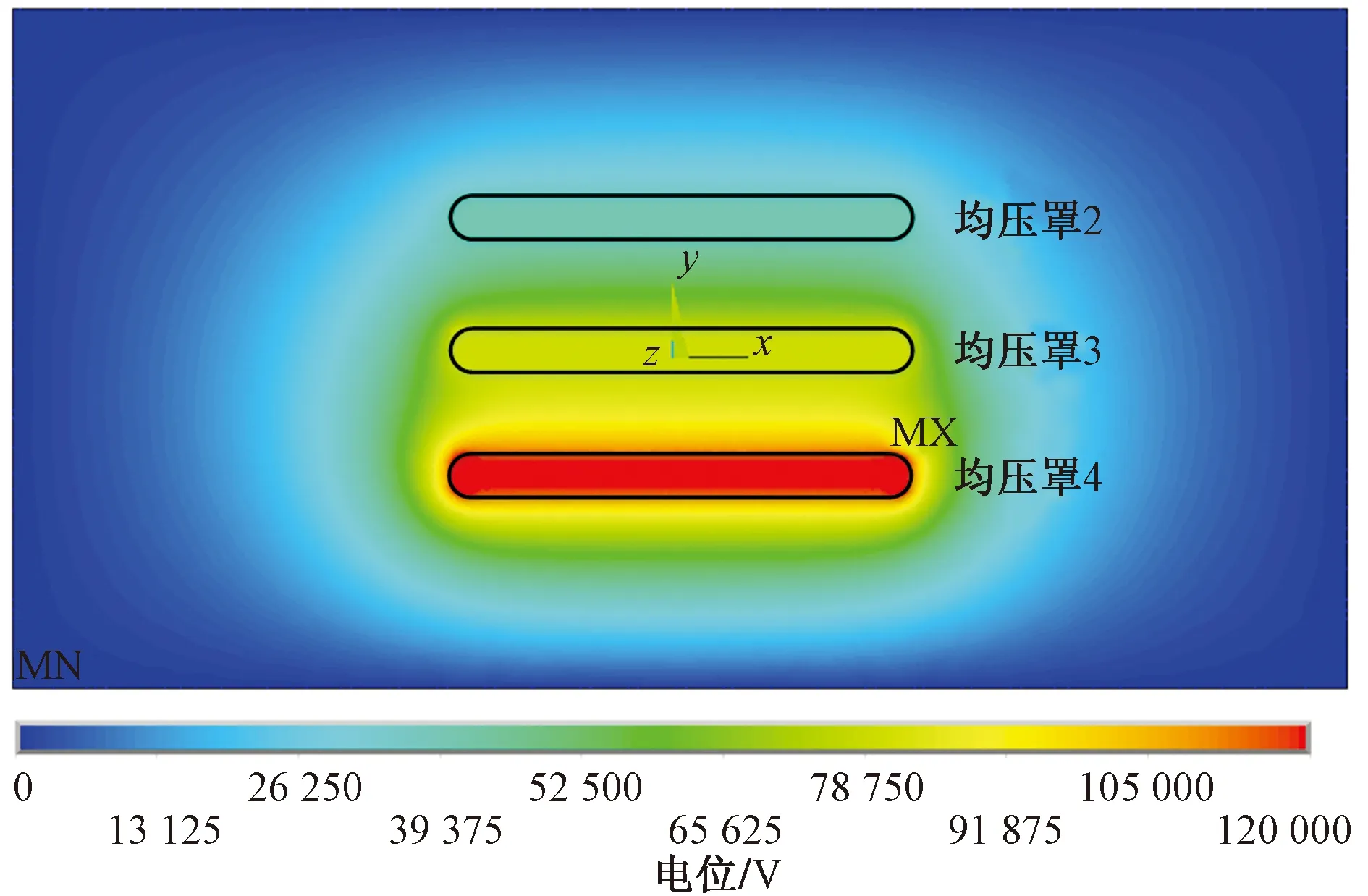
图15 整体电位分布Fig.15 Overall potential distribution

图16 第三层屏蔽罩附近电位分布Fig.16 Potential distribution near the third layer shield

3号屏蔽罩附近及光纤电场分布如图17所示，可以看出，3号屏蔽罩、盖板及其固定架等电位，电场强度为0，光纤上电场强度最大值为0.037 kV/mm。

图17 3号屏蔽罩附近电场分布Fig.17 Electric field near the third layer shield

图18 光纤序号图Fig.18 Order number of optical fiber

由此可知，在光纤正常安装的情况下，并不会产生局部放电。

4.2 不同光纤电阻率差异对电场分布的影响

光纤在实际运行过程中，常常由于外界环境及电场的作用而使得光纤电阻率分布非线性。本节将比较不同光纤电阻率差异对于电场分布的影响，如图18所示，为方便仿真，将第三层屏蔽罩处的每根光纤等分为上下两部分，依次编号为1～4号光纤，其中1、3号为一条光纤，2、4号为一条光纤，通过光纤盖板将其隔开。

根据实测数据，光纤电阻率为106～1012Ω·m，由于盖板上下部分光纤电场分布相同，这里仅分析1、2号光纤。

4.2.1 不同光纤电阻率不一致时

设1号光纤电阻率为1012Ω·m，且均匀分布，2号光纤电阻率为106Ω·m，且均匀分布。仿真结果如图19所示，可以看出，两根光纤电位分布一致，呈沿轴向均匀压降的线性关系，而电场强度相等，沿轴向均为0.037 kV/mm。

这主要是因为两根不同光纤首尾两端电位相同，而空气电阻率远大于光纤，光纤在空气中相当于良导体，单根光纤的电位分布仅决定自身电阻率的均匀度，而与其他光纤的电阻率大小无关。不同光纤间只要保证各自光纤沿轴向方向电阻率是均匀分布的，两根光纤上相同位置的电位和电场分布便是相同的。

图19 改变1、2号光纤电阻率后光纤电位与电场分布Fig.19 Distribution of fiber potential and electric field after changing the resistivity of No. 1 and No. 2 fiber

图20 1号光纤上下两部分比例图Fig.20 Cale diagram of upper and lower parts of No.1 optical fiber

4.2.2 同一光纤电阻率分布不一致时

研究2号光纤电阻率均匀分布且电阻率为1012Ω·m，1号光纤电阻率分布不一致时的电场分布情况。将1号光纤分为上下两部分，其中1号光纤靠近盖板部分占光纤总长度的10%，如图20所示。赋予1号光纤上下两部分不同的电阻率值，开展两种极端情况下的电场分析。

(1)1号光纤上部光纤电阻率为1012Ω·m，下部光纤电阻率为106Ω·m。仿真结果如图21所示，可以看出，1号光纤轴向电场强度最大值为0.04 kV/mm，相较于电阻率均布分布的电场畸变率8.1%；两根光纤轴向路径上电位、电场分布如图22所示，两者相同位置上最大电压差为1.06 kV，根据空气的击穿场强，当两根光纤未有效接触，且两者间距小于0.35 mm，会引发光纤之间的局部放电。

1号光纤上下部电阻率分别为1012、106 Ω·m图21 两根光纤电位与电场分布Fig.21 Tential and electric field distribution of two optical fibers

1号光纤上下部电阻率分别为1012、106 Ω·m图22 两根光纤轴向路径上电位与电场对比Fig.22 Comparison of potential and electric field on the axial path of two optical fibers

(2)1号光纤下部光纤电阻率设为1012Ω·m，上部光纤电阻率设为106Ω·m。仿真结果如图23所示，可以看出，1号光纤电位分布非线性，轴向电场强度最大值为0.54 kV/mm，相比光纤电阻率分布均匀情况下的电场强度，其畸变率为1 359.5%。

图24为两根光纤轴向路径上电位、电场对比，可以看出，两根光纤相同位置电位差最大值为13.944 kV。根据空气的击穿场强可知，当两根光纤未有效接触，且两者间距小于4.6 mm，会引发光纤之间的局部放电。

1号光纤上下部电阻率分别为106、1012 Ω·m图23 两根光纤电位与电场分布Fig.23 Potential and electric field distribution of two optical fibers

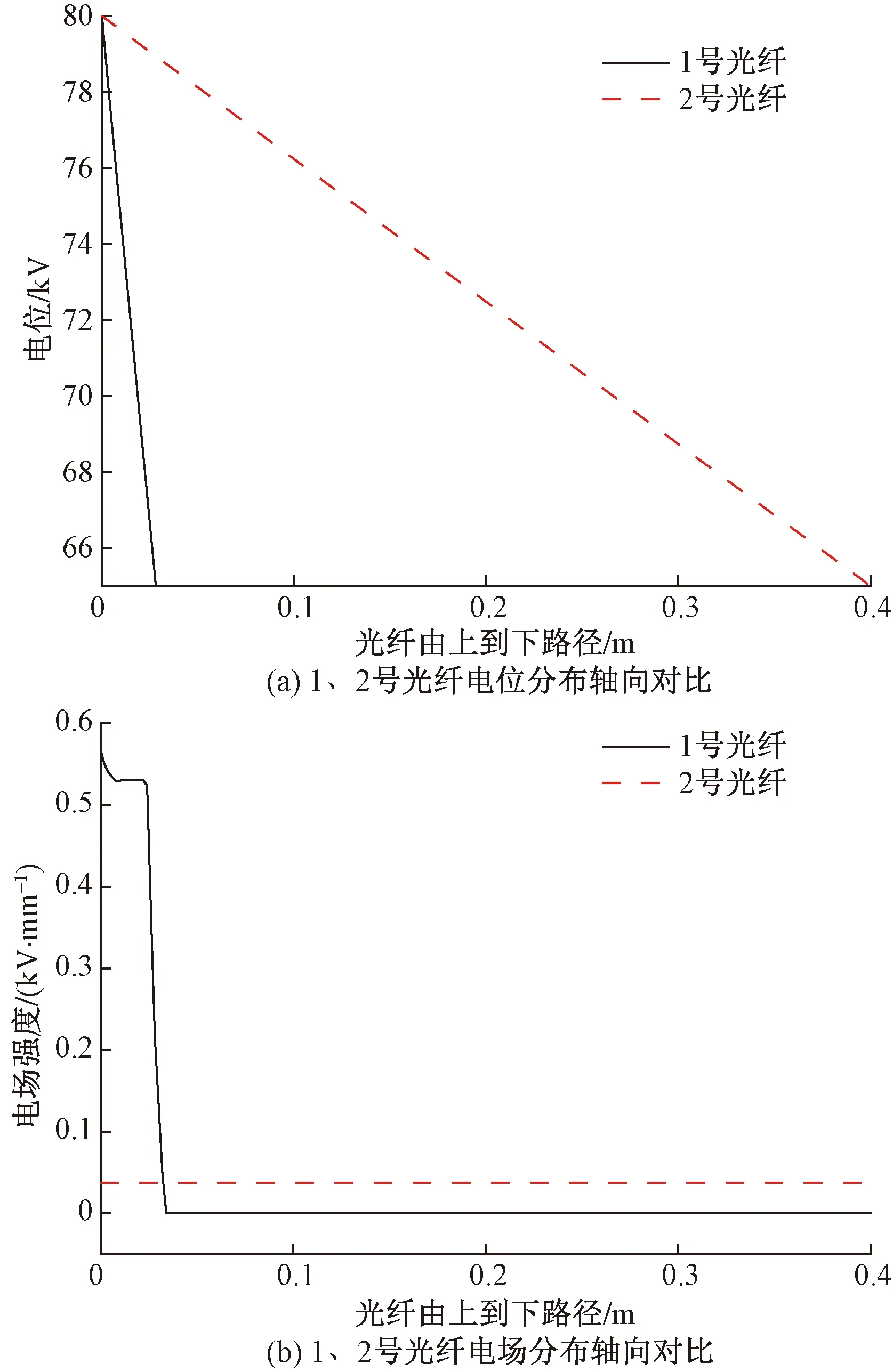
1号光纤上下部电阻率分别为106、1012 Ω·m图24 两根光纤轴向路径上电位与电场对比Fig.24 Comparison of potential and electric field on the axial path of two optical fibers

综上所述，同一光纤电阻率分布不一致时，光纤的轴向电场强度将存在畸变，不同光纤之间会产生电压差，当距离较近，光纤之间的场强大于空气击穿场强时，会发生局部放电。当距离盖板近的区域的光纤电阻率较大，而远离盖板区域的光纤电阻率较小时，光纤间更易发生局部放电。

4.2.3 盖板处接触不良对电场分布的影响

本节将研究光纤与盖板未有效连接的工况，即盖板内的光纤电位未被有效钳制到屏蔽罩的电位，分析此工况下盖板内光纤电场分布情况。设置单一光纤穿过盖板，并与盖板间存在间隙(间距为1 mm)未有效接触，如图25所示。

图25 光纤与盖板未有效接触Fig.25 The optical fiber is not in effective contact with the cover plate

(1)当光纤电阻率分布一致时，仿真结果如图26所示。可以看出，盖板内的光纤电位自上而下从77.1 kV上升到82.9 kV，光纤与盖板间存在电位差，且盖板上下两端的电位差最大，为2.9 kV，电场强度最大值达到了2.9 kV/mm，基本接近空气的击穿场强，若光纤与盖板的距离更近的情况下，光纤与盖板之间极有可能形成局部放电。

图26 盖板内光纤电阻率均匀时的电位分布Fig.26 Potential distribution when the resistivity of optical fiber inside and outside the cover plate is uniform

图27 盖板内光纤电阻率比空气中光纤电阻率大时的电位分布Fig.27 Potential distribution when the resistivity of optical fiber in cover plate is greater than that of optical fiber in air

(2)当盖板内光纤电阻率与其他部位不同时，即将1号光纤盖板内电阻率设为1012Ω·m，其他部位电阻率设为1010Ω·m，此时光纤电位分布如图27所示。可以看出，盖板中的光纤电位分布为70～91 kV，光纤与盖板间电位差增大，最大为11 kV，此时光纤与盖板间的最大电场强度为11 kV/mm，相比于光纤电阻率一致时的电场强度，其畸变率为279.3%，远超过空气击穿场强，更易发生局部放电。

5 结论

针对换流阀触发光纤的现场故障，通过对光纤故障点处的宏观与微观分析，确定其为局部放电故障。利用有限元法对光纤进行电场仿真，分析了不同光纤电阻率差异对电场分布的影响，以及盖板与光纤接触不良时对光纤电场分布的影响，得出如下结论。

(1)当光纤与盖板接触良好，且光纤轴向电阻率分布一致时，光纤表面电场强度极低，不会发生局部放电。

(2)当光纤轴向电阻率分布不一致时，光纤之间同位置处存在电位差，当距离较近，光纤之间的场强大于空气击穿场强时，会发生局部放电。

(3)当光纤与盖板未有效接触，盖板内的光纤电位没有被钳制时，光纤与盖板间会存在电位差，且盖板上下两端的电位差最大，此处更易发生局部放电。

(4)定期检测每根光纤电阻率，防止由于光纤轴向电阻率不一致而导致的光纤与光纤之间产生的局部放电。

(5)在安装盖板时，需要保证光纤排列整齐，确保盖板钳制每条光纤电位，从而防止光纤与盖板之间发生局部放电。