基于无人机多光谱影像的夏玉米SPAD估算模型研究

冯 浩 杨祯婷 陈 浩 吴莉鸿 李 成 王乃江

(1.西北农林科技大学水利与建筑工程学院， 陕西杨凌 712100；2.中国科学院水利部水土保持研究所， 陕西杨凌 712100；3.西北农林科技大学中国旱区节水农业研究院， 陕西杨凌 712100；4.中国电建集团西北勘测设计研究院有限公司， 西安 710065)

0 引言

近年来，随着精准农业的发展，农业遥感技术应用的广度和深度不断扩展，不仅要求能获得传统的产量、种植面积，还要能够及时获取作物的健康状况，进而指导田间管理[1-2]。叶绿素是植物进行光合作用的主要色素，是表征植物营养胁迫、光合作用能力的重要因子，是进行作物长势监测的重要指标之一[3-4]。叶绿素相对含量(Soil and plant analyzer development，SPAD)与叶绿素含量密切相关，可以反映植物叶片叶绿素含量，测量SPAD是获取叶绿素含量的一种无损、便捷的方法[5-6]。

目前遥感数据源主要有地物光谱仪、无人机以及卫星。地物光谱仪主要进行点尺度数据的获取，难以进行大范围的观测，同时数据采集会对农田造成一定程度的破坏。卫星遥感数据时间和空间分辨率均较大，所以卫星遥感更适合区域尺度产量、种植面积和作物长势等的监测。相比之下，无人机具有成本低、灵活性高、机动性强、时空分辨率高、操作方便等特点，进行田块尺度作物长势监测有无可比拟的优势[7]。

在利用遥感数据估算SPAD的研究中，主要有3种方法：经验模型、物理模型以及经验-物理耦合模型[8]，其中，以有关经验模型的研究居多[9-14]。乔浪等[12]从无人机RGB图像中提取了10种颜色特征和6种纹理特征，采用BP神经网络建立玉米冠层叶绿素含量检测模型，模型的决定系数为0.72。牛庆林等[13]将可见光植被指数与多光谱植被指数结合，利用逐步回归和随机森林回归方法估算SPAD值，模型的决定系数均能达到0.88以上。

经验模型是建立基于冠层影像得到的光谱指数、植被指数等与实测SPAD之间的数学统计关系，参数少，模型简单，应用简便，也能够取得精度较高的建模结果，但缺乏物理意义，不同时间地点建模结果相差大，难以移用。近年来，有研究者尝试将气象数据和植被指数结合，建立分层线性模型进行产量等的估算，取得了一些成果。LI等[15]结合高光谱和气象数据，利用分层线性模型建立了小麦产量和品质的年际可扩展预测模型，结果表明，分层线性模型是一种提高冬小麦产量和籽粒蛋白质含量预测稳定性的方法。ZHU等[16]以归一化植被指数和气象数据作为输入参数，建立分层线性模型估算2016—2019年吉林省玉米产量，结果显示，分层线性模型优于线性回归和多元线性回归方法。XU等[17]将植被指数与欧洲中尺度天气预报中心气象数据使用分层线性模型耦合，构建河北省4个小麦产区籽粒蛋白质含量预测模型，研究结果表明，使用HLM方法(R2=0.524)预测的籽粒蛋白质含量比线性模型(R2=0.286)显示出更高的准确性。

以上研究表明，加入气象数据可以有效提高产量和籽粒蛋白质含量的模型精度，提升经验模型在时空上的通用性。然而，以上研究都是与一元线性或多元线性模型做对比，融合了气象数据的分层线性模型是否比其他模型精度高需要进一步探究。同时，对于能否提升SPAD估算模型的精度也是未知的。因此，本研究将基于无人机多光谱影像提取植被指数，以筛选后的植被指数作为模型输入变量，采用偏最小二乘法、随机森林回归和分层线性模型分别构建2020年夏玉米拔节期、抽雄期、灌浆期以及全生育期的SPAD估算模型，进行模型评价，选出最优估算模型，以期为SPAD估算提供参考。

1 估算模型构建

1.1 研究区概况

研究区位于陕西省杨凌区西北农林科技大学灌溉试验站(34°20′N，108°24′E，海拔521 m)。该区域属于暖温带半湿润气候区，多年平均气温为12.9℃，多年平均降水量为630 mm，降水集中在7—10月。试验采用随机区组设计，根据施氮量不同和是否追肥共设置7个处理：CK、N1-1、N1-2、N2-1、N2-2、N3-1、N3-2。施氮量分为4个水平，分别为CK(不施肥)、N1(105 kg/hm2)、N2(210 kg/hm2)、N3(315 kg/hm2)；N1-1、N2-1、N3-1为氮肥全部基施，N1-2、N2-2、N3-2为60%氮肥基施，剩余40%在拔节期追施。每个处理设置3个重复，共21个小区，每个小区面积为20 m2。供试玉米品种为秦龙14，生育期内不灌溉，施磷肥量90 kg/hm2。研究区位置及试验设置如图1所示。

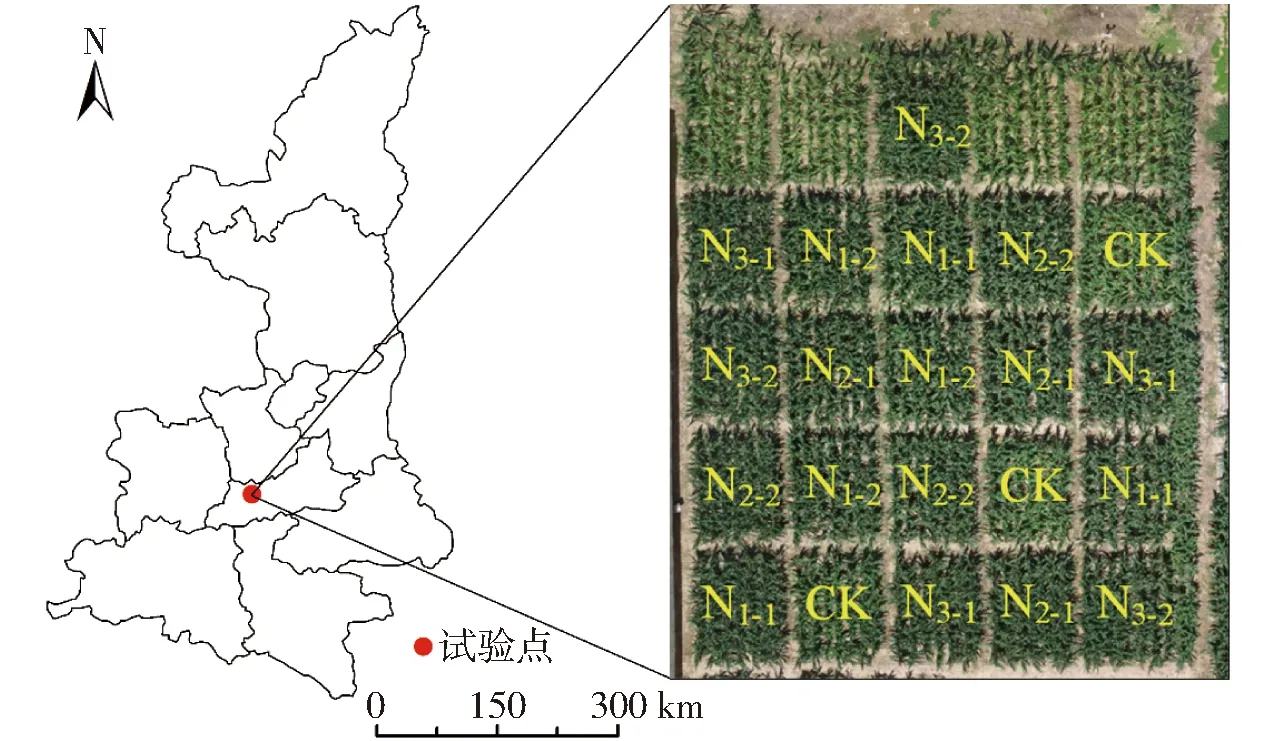
图1 研究区概况Fig.1 Location of study area and experimental design

1.2 无人机影像获取与预处理

本研究采用大疆M600 Pro搭载RedEdge多光谱相机作为无人机多光谱影像采集系统，如图2所示，多光谱相机的参数如表1所示。

图2 无人机多光谱影像采集系统Fig.2 UAV for acquiring multispectral images

分别于2020年7月20日(拔节期)、2020年8月9日(抽雄期)、2020年8月26日(灌浆期)进行无人机影像采集。采集时，在晴朗无云的天气条件进行，飞行时间选择11：00—13：00，设置飞行高度为30 m，航向重叠度为80%，旁向重叠度为80%。无人机在起飞之前，对灰板进行拍照，用于之后的辐射定标，拍照时避免其受阴影干扰。

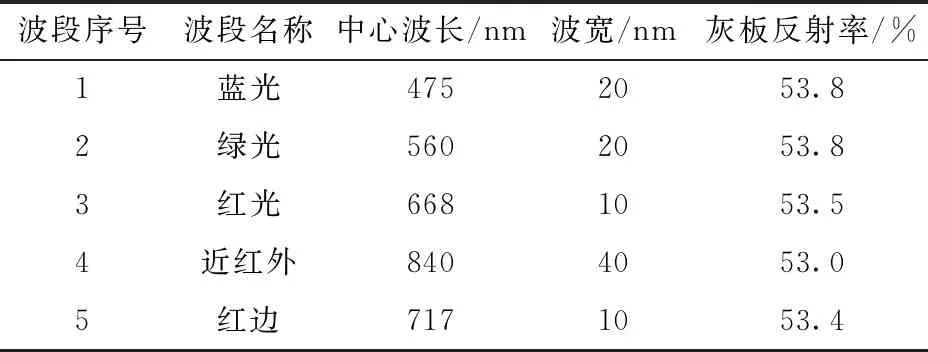
表1 多光谱相机参数及灰板对其中心波长的反射率Tab.1 Parameters of multispectral camera and reflectivity of calibrated reflectance panel to its center wavelength

筛选出包含试验区的单幅影像，使用Agisoft LCC公司开发的PhotoScan软件进行拼接，得到试验区各波段正射影像。将拼接好的各波段影像导入ArcGIS，采用

(1)

式中Ri——地面目标第i波段反射率

Di——地面目标第i波段DN值

Rbi——灰板第i波段反射率

Dbi——灰板第i波段DN值

进行辐射定标，将图像数字量化值(Digital number，DN)转化为反射率，从而得到各波段反射率影像。

1.3 植被指数选取与计算

结合前人的研究成果，选取了8种植被指数用于估算夏玉米SPAD值。各个植被指数的公式及来源如表2所示。

表2 植被指数汇总Tab.2 Definitions of vegetation indices

基于各波段反射率影像计算得到植被指数。进一步，采用植被指数阈值法剔除土壤背景，通过目视解译的方式确定每个植被指数中植被与土壤背景的阈值，经栅格计算器运算后剔除土壤背景。根据试验小区位置和大小构建矢量文件，统计矢量范围内植被指数的均值作为这一小区的植被指数。以上过程均在ArcGIS中完成。

1.4 田间数据获取

在无人机影像采集的同时进行SPAD的测量。使用SPAD-502Plus便携式叶绿素测定仪测量植株的穗位叶，在叶子中部避开叶脉随机选取5个位置测定，取平均值作为该植株的SPAD值，每个小区选7株进行测量，其平均值作为该小区的SPAD值。不同生育期获得的SPAD值样本特征如表3所示。

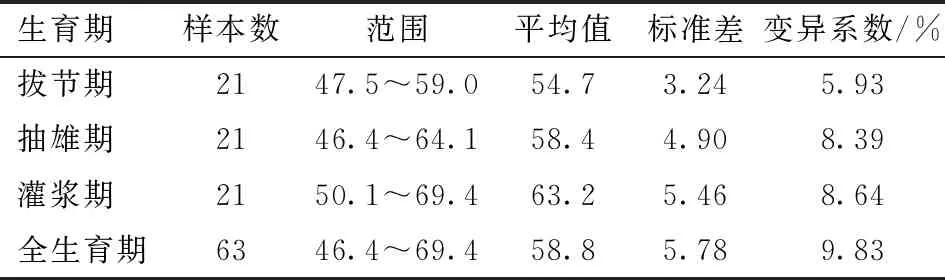
表3 SPAD值样本特征统计Tab.3 Descriptive statistics of SPAD values

1.5 模型构建方法

偏最小二乘法(Partial least squares，PLS)是一种通过最小化误差的平方和寻找一组数据最佳匹配函数的方法。它将相关性分析、主成分分析和多元线性回归等统计方法有效地结合起来，可以在自变量具有多重相关性和样本点个数较少的条件下建立模型。

随机森林回归(Random forest regression，RF)是利用多个决策树对样本进行训练并预测的一种机器学习算法，有很强的抗干扰能力和抗过拟合能力。同时，还具有训练速度快、无需对输入数据做处理等优点。

分层线性模型(Hierarchical linear model，HLM)是由不同层次的自变量解释同一变量的一体化模型，是一种具有分层或嵌套数据结构的混合模型形式。在本研究中，采用包含两层的分层线性模型，第1层模型是基于植被指数的SPAD估算模型，第2层模型中因变量是第1层模型的截距和斜率，气象要素(降雨量、最高气温)作为自变量，具体形式为

SPADmj=ψ0j+ψ1jOSAVImj+ψ2jCIremj+emj

(2)

其中

(3)

式中ψ0j——第1层模型的截距

ψ1j、ψ2j——OSAVI、CIre的斜率

emj——随机误差

Tmaxj、Pj——最高气温、降雨量

γ00、γ10、γ20——第2层模型的截距

γ01、γ11、γ21——最高气温的斜率

γ02、γ12、γ22——降雨量的斜率

u0j、u1j、u2j——随机误差

1.6 模型精度评价

采用决定系数(Coefficient of determination，R2)、均方根误差(Root mean square error，RMSE)和相对分析误差(Relative prediction deviation，RPD)3个指标评价模型反演精度。其中，R2越大，RMSE越小，表明模型效果越好。而RPD对模型的评价分为3个等级：当RPD<1.4时，认为模型无法对样本进行预测；1.4≤RPD<2时，认为模型效果一般，可以用来对样本进行粗略预测；RPD≥2时，认为模型具有极好的预测能力。

2 结果与分析

2.1 SPAD与植被指数的相关性分析

计算得到拔节期、抽雄期和灌浆期不同试验处理下各小区的8个植被指数，与相对应的田间实测SPAD组成数据集。分别对这3个生育期的SPAD与植被指数进行相关性分析，结果如图3所示。

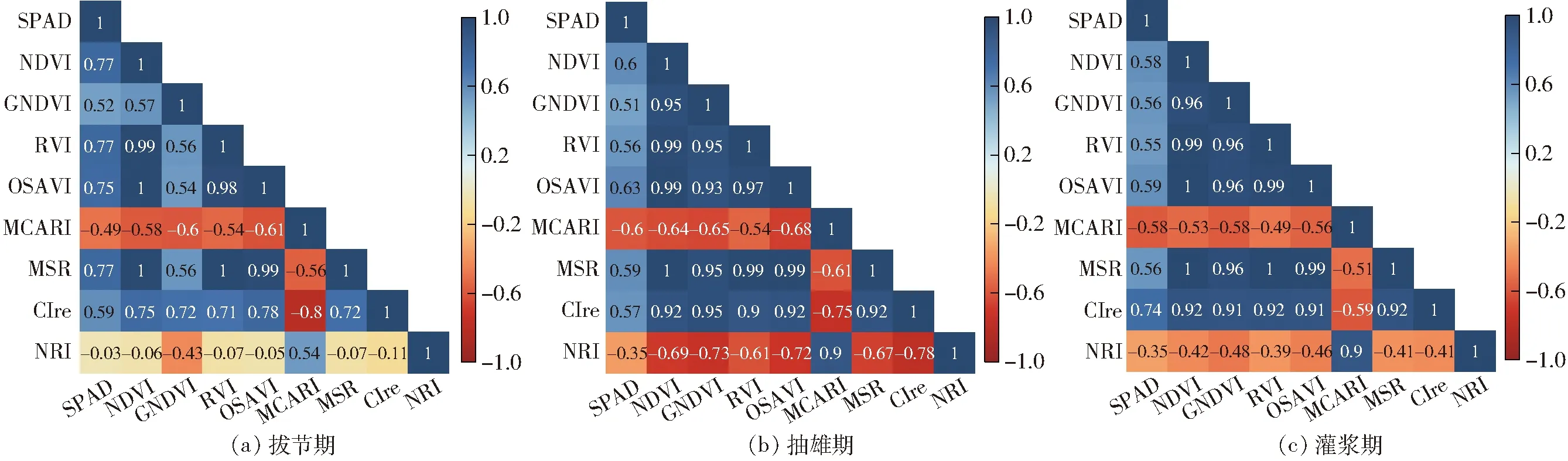
图3 植被指数与SPAD的相关系数Fig.3 Correlation coefficients between vegetation indices and SPAD values

由图3可知，在3个生育期，NDVI、GNDVI、RVI、OSAVI、MSR和CIre与SPAD均呈正相关关系，而MCARI、NRI与SPAD之间均是负相关关系。从图3a中可以看出，在拔节期，NDVI、RVI、OSAVI、MSR、CIre的相关系数为0.59～0.77，在0.01水平上显著；GNDVI、MCARI与SPAD有较低的相关性，相关系数分别为0.52和-0.49，在0.05水平上相关性显著；NRI与SPAD的相关系数只有-0.03，关系不显著。由图3b可知，在抽雄期，OSAVI与SPAD的相关系数最高，为0.63；NRI最低，为-0.35。GNDVI与SPAD的相关性在0.05水平上显著，NRI不显著，其余在0.01水平上显著。由图3c可以看出，在灌浆期，NRI与SPAD的相关系数仍旧是最低的，为-0.35，相关关系不显著；除此之外的植被指数与SPAD均具有较强的相关关系，在0.01水平上显著，其中，CIre与SPAD的相关系数最高，为0.74。

综合来看，NRI与SPAD的相关性较差；其余植被指数与SPAD呈现较强且稳定的相关关系，均能达到0.05水平上显著。

2.2 反演建模

利用PLS、RF分别建立拔节期、抽雄期、灌浆期的SPAD反演模型，采用PLS、RF和HLM分别建立全生育期SPAD的估算模型，建模和验证结果如表4所示。PLS、RF、HLM模型预测值和实测值的关系分别如图4～6所示。

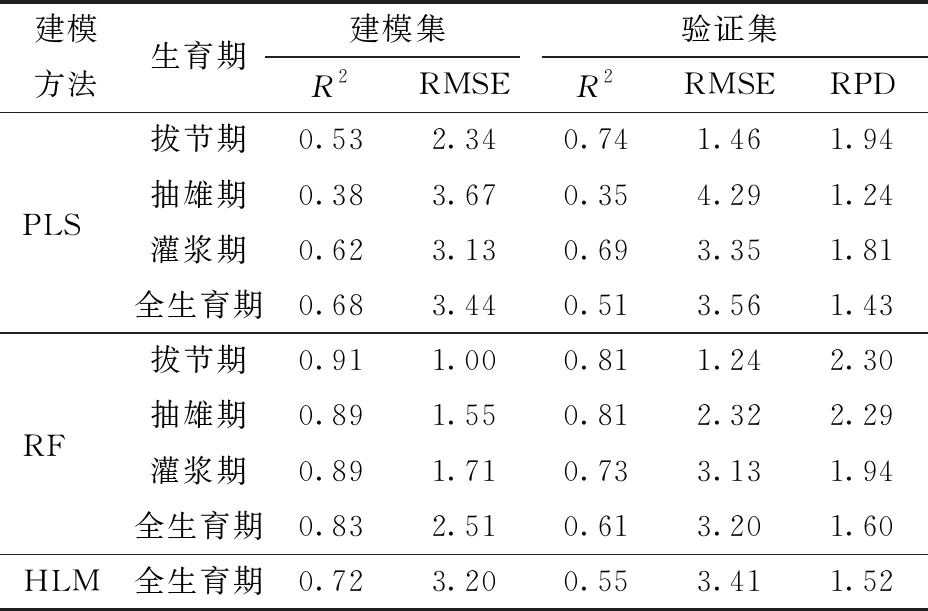
表4 不同估算模型的建模和验证结果Tab.4 Calibration and validation results of different estimation models

图4 基于偏最小二乘法的SPAD估算模型预测值和实测值的关系Fig.4 Relationships between predicted values of SPAD based on partial least squares method and measured values

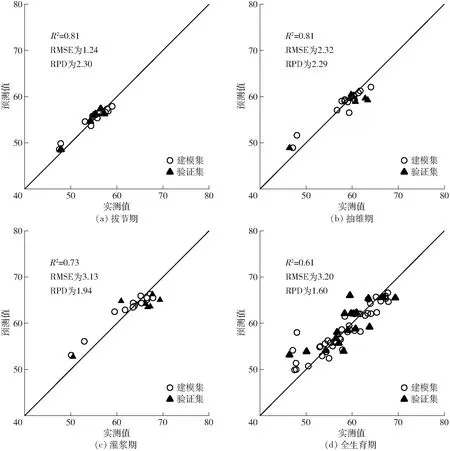
图5 基于随机森林的SPAD估算模型预测值和实测值的关系Fig.5 Relationships between predicted values of SPAD based on random forest and measured values

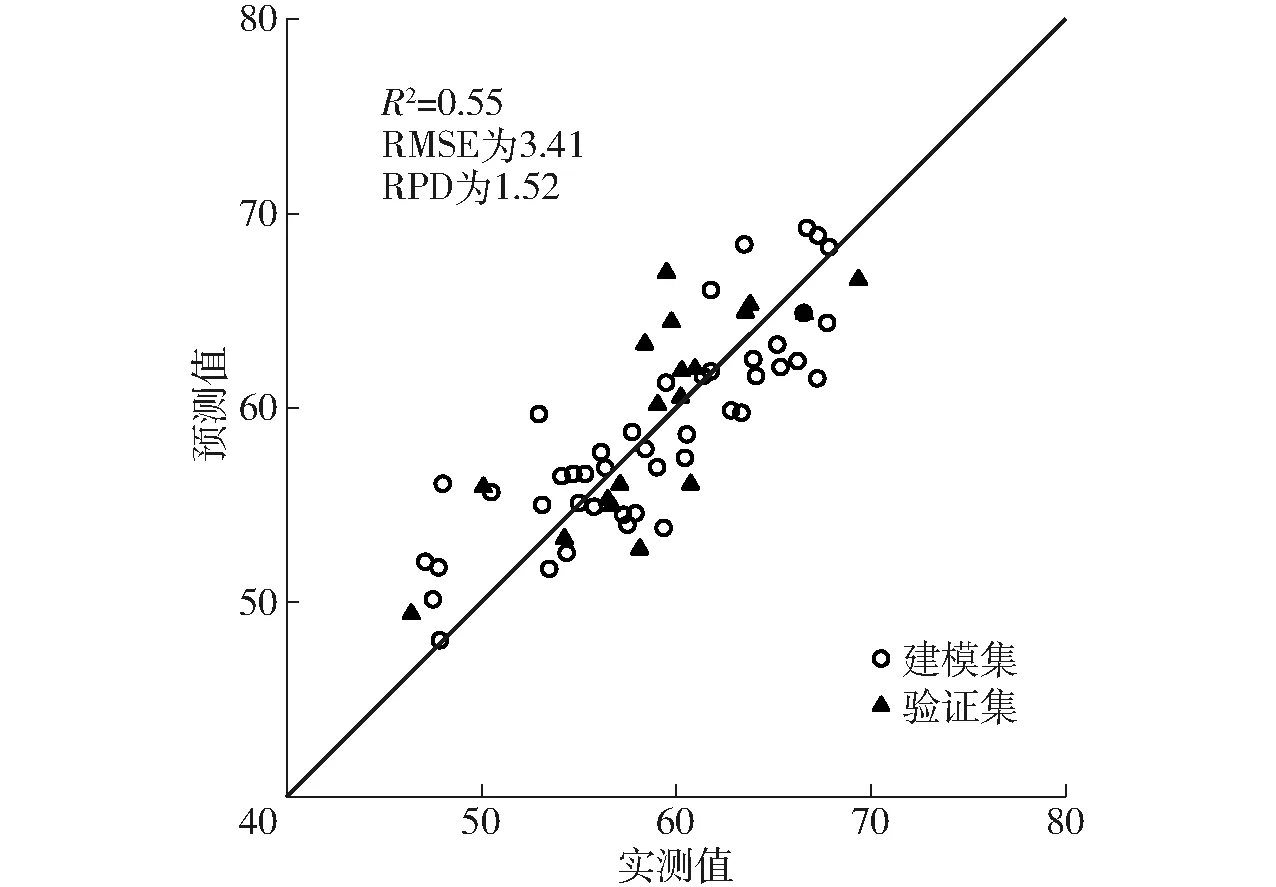
图6 基于分层线性模型的SPAD估算模型预测值和 实测值的关系Fig.6 Relationships between predicted values of SPAD based on hierarchical linear model and measured values

基于SPAD与植被指数的相关性分析结果，选择NDVI、GNDVI、RVI、OSAVI、MCARI、MSR、CIre这7个植被指数进行PLS和RF建模。从表4中可以看出，同一方法对不同生育期SPAD的反演效果存在差异，同一生育期中不同方法的表现也不同。就生育期来看，在拔节期，RF模型的建模集R2为0.91，验证集R2为0.81，均高于PLS建模集和验证集的R2；RF模型建模集和验证集的RMSE均低于PLS模型，分别为1.00和1.24；RF模型的RPD大于2，PLS模型的RPD为1.94，说明RF模型对SPAD具有极好的预测能力，而PLS模型效果一般，可以对SPAD进行粗略估计。在抽雄期，RF模型的建模集和验证集R2分别比PLS模型高0.51和0.46，RMSE分别低2.12和1.97，RPD显示RF模型具有极好的预测能力，而PLS模型无法对SPAD进行预测。在灌浆期，RF模型各个评价指标均表明RF模型精度比PLS模型高，其中，两个模型在验证集上表现出差不多的效果，两个模型均为一般模型。就建模方法来看，和PLS模型相比，RF模型对各生育期的SPAD反演效果都有不同程度的提升，尤其是在抽雄期。PLS和RF模型精度均在拔节期为最高，PLS模型在抽雄期表现最差，验证集R2只有0.35，不能用来反演SPAD，而RF模型在各生育期表现较为稳定，在灌浆期反演精度相对较低。

由于用以上7个植被指数进行HLM建模时，出现过拟合现象，建立的模型在验证集上效果很差，所以基于SPAD与植被指数的相关性分析和RF模型的变量重要性分析，选择OSAVI和CIre作为输入变量建立HLM模型。在全生育期，不论是建模集还是验证集，R2从大到小依次为RF、HLM、PLS，RMSE从小到大分别为RF、HLM、PLS，RPD从大到小为RF、HLM、PLS，说明相比之下RF模型对SPAD的反演效果最好、精度最高，但3个模型对SPAD的反演效果均一般，只能进行粗略估计。

2.3 基于最佳估算模型的SPAD可视化制图

与分生育期模型相比，全生育期模型在各生育期的预测精度有所降低，所以将分生育期RF模型应用到各生育期，得到不同生育期试验地各小区的SPAD空间分布图，如图7所示。

图7 不同生育期SPAD空间分布图Fig.7 SPAD spatial distribution maps in different growth stages

整体上呈现出从拔节期到抽雄期再到灌浆期SPAD持续增大的趋势，这与实测结果一致。在不同生育期，CK处理的SPAD均最小，集中在48.5～52；不同施氮处理，N1处理的SPAD较低，而N2和N3处理的比较相近；相同施氮水平下的追肥与不追肥处理差异不明显。图7中信息与实际测量结果的规律一致，说明基于无人机多光谱影像建立经验模型进行田块尺度夏玉米SPAD估算是可行的。

3 讨论

本研究基于无人机获取的多光谱影像提取8个植被指数，经筛选后作为模型输入变量，利用PLS、RF分别建立拔节期、抽雄期和灌浆期的SPAD反演模型，采用PLS、RF和HLM进行全生育期SPAD建模。

CIre与SPAD的相关系数波动大，且在灌浆期明显高于其他植被指数。CIre是红边波段和近红外波段构建的植被指数。首先，HORLER等[26]研究发现波长700 nm左右的反射率与叶绿素有良好的相关性，这使得CIre与SPAD具有强相关性。其次，红边波段对叶绿素含量的变化非常敏感[27]，在植被指数中引入红边波段，可以增强其对叶绿素含量变化的敏感性[28]。此外，红边波段参与构建的植被指数多数容易受外界环境因素的影响[29-30]。因此，CIre与SPAD的相关性又具有不稳定性。

各个生育期的最优模型均是RF模型，主要原因是随机森林算法自身的优越性[31]。它对数据的包容力强，并且随机选取数据和待选特征，构建多个决策树对样本进行训练，最终取每个决策树预测值的平均值作为最终结果，因此，使得模型具有较高的精度以及很强的抗干扰能力[32-33]。RF模型在很多研究中都表现较好，姚雄等[34]研究表明RF模型为马尾松林叶面积指数的最佳估测模型，程千等[35]利用无人机多时相植被指数估测冬小麦产量，RF模型估测精度最高，且稳定性更好。偏最小二乘法和随机森林回归都在拔节期达到最佳，原因可能是拔节期数据分布好，变异系数小，而到夏玉米生育中后期对照组和施肥的SPAD值差距拉大，变异系数增大。

HLM模型结合了夏玉米生育期的气象数据(降雨量、最高气温)和多光谱数据，就本研究来看，HLM模型介于PLS模型和RF模型之间。相比于PLS模型，HLM模型对SPAD估算精度有所提升，而和RF模型相比，HLM模型精度稍差一些。这与已有研究结果相类似，HLM模型可以一定程度提升线性模型的估算精度和稳定性[15-17]。

分层线性模型为无人机遥感数据估算SPAD提供了新的方向，同时它也存在着巨大的潜力。本研究中，HLM模型融合了降雨量和最高气温这两个气象因子，还应进一步关注其他气象参数对SPAD的影响，例如太阳辐射，从而提高SPAD估算精度。同时，如果考虑更多的输入参数，HLM模型的复杂性将增加，所以如何平衡好模型的精度和复杂程度也是一个值得探究的问题。

4 结论

(1)在本研究选取的8个植被指数中，除NRI之外，NDVI、OSAVI、GNDVI、RVI、MCARI、MSR、CIre与SPAD均显著相关。其中，OSAVI、NDVI与SPAD呈现出较强且稳定的相关性，在拔节期、抽雄期和灌浆期的相关系数都较高；灌浆期，CIre表现突出，相关系数达到0.74。

(2)各个生育期的最优模型均是RF模型，在拔节期、抽雄期、灌浆期和全生育期，验证集R2分别为0.81、0.81、0.73、0.61，RMSE分别为1.24、2.32、3.13、3.20。和PLS模型相比，RF模型在抽雄期极大提升了估算精度，PLS模型验证集的R2、RMSE、RPD分别为0.35、4.29、1.24，RF模型的R2、RMSE、RPD分别为0.81、2.32、2.29。

(3)PLS模型在各生育期表现不稳定，特别是在抽雄期，精度最低，而RF模型在各生育期表现较为稳定，PLS和RF模型精度均在拔节期为最高。与各生育期分别建立的估算模型相比，全生育期模型的估算精度有所降低。

(4)对于SPAD估算模型，将降雨量、最高气温这两个气象因子与植被指数耦合的HLM模型可以一定程度提升线性模型的估算精度和稳定性，但其精度低于RF模型。