基于蜻蜓算法的铁路货运量预测模型研究
欧雅琴,余 雷
(巢湖学院 工商管理学院,安徽 巢湖 238024)
铁路货运量预测对区域经济和国家经济发展规划具有重要作用,可以预测未来铁路货运量的发展趋势并判断出未来货运量的大致概况,高精度的铁路货运量预测可以为运输企业的运营决策和铁路部门发展规划提供科学决策的依据和参考[1]。目前,铁路货运量预测的方法有粗糙集、分形理论、灰色理论、混沌理论、时间序列模型、马尔科夫模型、神经网络、支持向量机和长短期记忆(Long Short-Term Memory,LSTM)神经网络等[2]。很多学者对铁路货运量和客运量预测进行了研究。文献[3]将小波降噪和灰色GM(1,1)模型相结合,首先通过小波降噪消除铁路货运量原始数据中存在的噪声,之后运用灰色GM(1,1)模型对消除噪声之后的货运量数据进行预测,与灰色GM(1,1)模型相比,小波灰色GM(1,1)模型拟合效果更好,且具有更高的预测精度。文献[4]针对灰色Verhulst模型性能受其背景参数选择的影响,提出粒子群算法优化灰色Verhulst模型的铁路货运量预测方法,与径向基神经网络、灰色Verhulst模型和GM(1,1)模型相比,改进的灰色Verhulst模型可以有效提高预测精度、减小误差。文献[5]针对不同时期货运数据的特点,建立了LSTM多变量货运量预测模型,与BP神经网络和ARIMA模型相比,LSTM模型的预测效果更佳。文献[6]为了提高LSTM模型的铁路货运量预测精度,提出了基于乘积季节模型与引入注意力机制的LSTM组合预测模型,2005年至2018年全国铁路月度货运量预测结果表明,组合模型预测精度优于单一乘积季节模型和单一LSTM模型。
蜻蜓算法[7](Dragonfly Algorithm,DA)是受蜻蜓的动、静态行为启发所提出的一种新型群智能寻优算法。针对LSTM网络性能受隐含层神经元数量、分块尺寸、最大训练周期数以及学习率的影响,提出一种基于改进的蜻蜓算法(Improved DA)优化LSTM的铁路货运量预测模型。
1 LSTM神经网络
LSTM神经网络[8-9]克服了循环神经网络(Recurrent Neural Networks,RNN)难以训练和梯度消失问题,其网络结构如图1所示。

图1 LSTM网络结构图
图1中,在t时刻LSTM模型的输入为:t时刻LSTM的输入值xt;t-1时刻LSTM的输出值ht-1;t-1时刻的门控单元状态Ct-1。LSTM模型的输出为:t时刻LSTM的输出值ht;t时刻的门控单元状态Ct。遗忘门、输入门以及输出门计算公式为:
ft=σ(Wfxt+Wfht-1+bf)
(1)
it=σ(Wxxi+Wiht-1+bi)
(2)
Gt=tanh(Wcxt+Wcht-1+bc),
(3)
Ot=σ(Woxt+Woht-1+bo),
(4)
式(1)—(4)中,σ和tanh为激活函数;ft、it和Ot分别为遗忘门、输入门以及输出门状态计算结果。Wf、Wi和Wo为遗忘门、输入门以及输出门的权重矩阵;bf、bi和bo为遗忘门、输入门以及输出门的偏置项;Wc为输入单元状态的权重矩阵;bc为输入单元状态的偏置项;Gt为t时刻输入的单元状态。为实现回归预测,则在LSTM网络的基础上加上一个线性回归层:
yt=Wyoht+by
(5)
式(5)中,yt为预测结果;by为线性回归层的阈值;Wyo为线性回归层的权重。
2 改进的蜻蜓算法
DA算法中,蜻蜓群体的运动包括分离、对齐、内聚、觅食和躲避天敌5种行为模式[10]:
分离:分离行为如公式(6)所示
(6)
式(6)中,X为当前蜻蜓个体的位置;N为附近蜻蜓个体的数量;Xj为第j个附近蜻蜓个体的位置;Si为第i个个体分离之后的位置。
对齐:对齐行为如公式(7)所示
(7)
式(7)中,Vj为第j个附近蜻蜓个体的速度;Ai为第i个个体对齐之后的位置。
聚集:聚集行为如公式(8)所示
(8)
式(8)中,Ji为第i个个体聚集之后的位置。
觅食:觅食行为如公式(9)所示
Fi=X+-X
(9)
式(9)中,X+为食物源的位置;Fi为第i个个体食物源的位置。
躲避天敌:躲避天敌行为如公式(10)所示
Ei=X-+X
(10)
式(10)中,X-为天敌的位置;Ei为第i个个体天敌的位置。
为了较为准确地模拟出蜻蜓的移动过程,步长向量dX和位置向量X被引入DA算法,步长向量dX计算公式为:
dXt+1=(s+Si+a×Ai+c×Ji+f×Fi
+e×Ei)+w+dXt
(11)
式(11)中,t为当前迭代次数;w为惯性权重;s、a、c、f和e分别为分离权重、对齐权重、聚集权重、觅食影响因子和天敌影响因子。
蜻蜓位置更新公式如下:
1)当附近有蜻蜓个体时,更新公式为:
Xt+1=Xt+dXt+1
(12)
2) 当附近无蜻蜓个体时,更新公式为:
Xt+1=Xt+levy(d)×Xt
(13)
式(13)中,d为问题维数;levy(d)函数为:
(14)
式(14)中,β为常数;r1和r2为[0,1]之间的随机数;Γ(x)=(x-1)!。
针对标准蜻蜓算法初始种群个体分布均匀性较差的问题,运用佳点集法改进蜻蜓算法的初始种群个体[11],保证初始种群个体能够均匀地分布在解空间内。假定所求优化问题的可行域为:
x∈[l,u],[l,u]={x∈Rd|lk≤xk≤uk,k=1,2,…,d}
(15)
若存在一个d维空间的单位立方体G,在G空间中取一点r=(r1,r2,…,ri),其中rk={2cos(2πk/p),1≤k≤d},p是满足(p-3)/2≥d的最小素数,这时r为单位立方体Gd空间中的佳点,那么r在G空间中的佳点集pM(i)={({r1i},{r2i},…,{rdi}),i=1,2,…,M},其中M为佳点的数量。佳点集在可行域中的映射关系如公式(16)所示:
(16)
3 基于Improved DA-LSTM的预测模型
3.1 适应度函数
针对LSTM网络性能受隐含层神经元数量(par1)、分块尺寸(par2)、最大训练周期数(par3)以及学习率LR(par4)的影响,提出一种基于改进的蜻蜓算法(Improved DA)优化LSTM预测模型,运用改进的蜻蜓算法(Improved DA)对LSTM模型参数进行优化选择,选择均方根误差(Root Mean Squared Error,RMSE)作为适应度函数fRMSE,Improved DA优化LSTM模型的适应度函数为:

(17)
式(17)中,Xobs和Xpred分别为实际值和LSTM模型预测值;m为样本数量;s.t为约束条件,主要限制隐含层神经元数量(par1)、分块尺寸(par2)、最大训练周期数(par3)以及学习率LR(par4)4个参数的搜索范围。
3.2 算法流程
改进的蜻蜓算法(Improved DA)优化LSTM模型的流程如图2所示。

图2 改进的蜻蜓算法(Improved DA)优化LSTM模型流程图
改进的蜻蜓算法(Improved DA)优化LSTM模型的算法流程如下。
Step1:Improved DA算法和LSTM模型参数初始化。最大迭代次数Tmax、当前迭代次数t、种群数量N、空间维数Dim;LSTM模型参数:par1∈[1,100]、par2∈[8,64]、par3∈[10,50]、par4∈[0.01,1]。
Step2:数据预处理。将数据集划分为训练集和测试集,并归一化处理。
Step3:初始化步长向量dX和位置向量X。将隐含层神经元数量(par1)、分块尺寸(par2)、最大训练周期数(par3)和学习率LR(par4)组成参数组合向量(par1,par2,par3,par4),随机初始化位置向量X。
Step4:更新惯性权重w、分离权重s、对齐权重a、聚集权重c、觅食影响因子f和天敌影响因子e和邻域半径r。
Step5:计算适应度值fRMSE,比较适应度值大小,确定蜻蜓的最优个体和最差个体,最优个体对应的位置向量X,即参数组合向量(par1,par2,par3,par4),最差个体被看作天敌。
Step6:寻找邻域内蜻蜓。通过计算欧式距离判定邻域内是否存在蜻蜓,若存在,则运用公式(6)和(7)更新步长向量dX和位置向量X;若不存在,则运用公式(8)更新位置向量X。
Step7:更新分离度S、对齐度A、内聚度C、食物因子F和天敌因子E。
Step8:更新步长向量dX和位置向量X。
Step9:若t>Tmax,则算法终止,输出LSTM模型最优参数组合向量(par1,par2,par3,par4);反之,则返回Step3。
4 铁路货运量预测分析
4.1 数据来源及评价指标
为评价改进的蜻蜓算法(Improved DA)优化LSTM模型进行铁路货运量预测的有效性和可靠性,实验数据来源于国家数据网http://data.stats.gov.cn/,选择我国2001—2019年铁路货运量数据为研究对象,影响因素包括公路货运量(万吨)、铁路营业里程(万公里)、铁路运输业就业人员数(人)、公路里程(万公里)、货物运输量(万吨)、货物周转量(亿吨公里)和国内生产总值(亿元)等。将2001—2014年的铁路货运量数据作为训练样本,2015—2019年的铁路货运量数据作为测试样本。
为衡量铁路货运量预测模型的性能,选择决定系数R2、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)和均方根误差作为评价指标[12]:

(19)

(20)

(21)
式(19)—(22)中,N为预测样本数量;Xobs和Xpred分别为某年铁路货运量的实际值和该年铁路货运量的预测值。决定系数R2数值越大,说明预测模型的效果越好。评价指标RMSE和MAPE,其数值越小,说明预测模型的效果越好;反之,预测效果越差。
4.2 结果分析
为评价改进的蜻蜓算法(Improved DA)优化LSTM模型进行铁路货运量预测的效果,将Improved DA-LSTM与DA-LSTM、PSO-LSTM、GA-LSTM、LSTM和BPNN对比,不同算法铁路货运量训练测试结果如图3所示和表1所示。

图3 铁路货运量训练测试结果图
由表1可知,在评价指标决定系数R2和RMSE上,Improved DA-LSTM预测模型的决定系
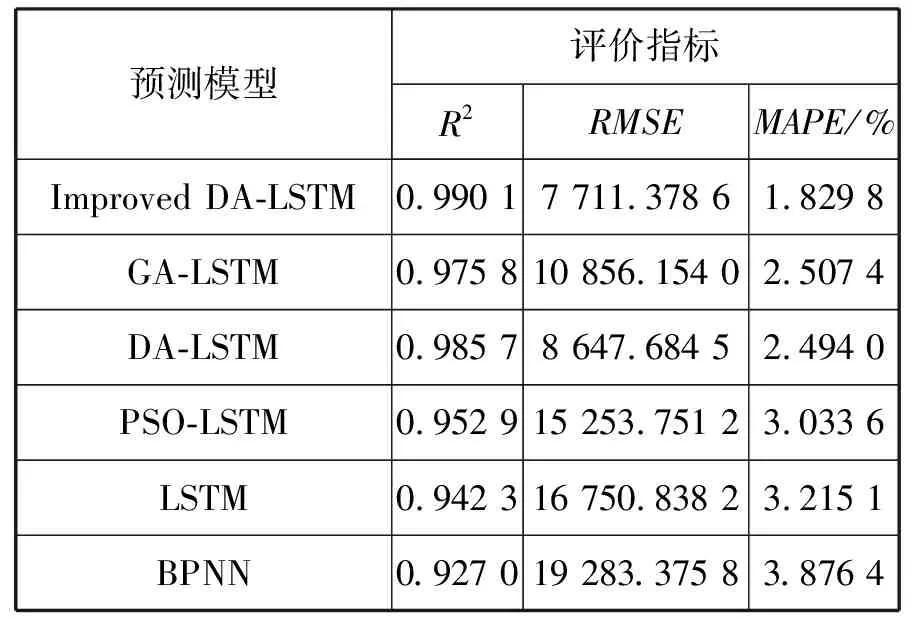
表1 铁路货运量预测结果
数R2和RMSE为0.990 1和7 711.378 6,与DA-LSTM、PSO-LSTM、GA-LSTM、LSTM和BPNN相比均有了一定程度上的提高,较BPNN和LSTM提高幅度最大,决定系数R2分别提高了0.063 1和0.047 8。在评价指标MAPE上,Improved DA-LSTM预测模型的MAPE为1.829 8%,与DA-LSTM、PSO-LSTM、GA-LSTM、LSTM和BPNN分别提高了0.664 2%、1.203 8%、0.677 6%、1.385 3%和2.046 6%。综合分析可知,在决定系数R2、RMSE和MAPE三个评价指标上,Improved DA-LSTM预测模型效果最优。
5 结论
为了提高铁路货运量的预测精度,提出一种基于改进的蜻蜓算法优化LSTM的铁路货运量预测模型。研究结果表明,与DA-LSTM、PSO-LSTM、GA-LSTM、LSTM和BPNN相比,Improved DA-LSTM可以有效提高铁路货运量预测的精度,为运输企业的运营决策和铁路部门发展规划提供科学决策的依据和参考,具有很高的应用价值和前景。

