离心压缩机蜂窝阻尼密封动力特性及转子稳定性*

姚 洁 孟继纲 胡 永 张忠伟

(沈阳鼓风机集团股份有限公司 辽宁沈阳 110869)

随着现代离心压缩机向高速化、大型化方向发展，机组在运转过程中受到传统迷宫密封气流激振力的作用，面临的转子失稳而导致停机或碰磨事故的风险大大上升。1985年，蜂窝阻尼密封首次用于解决航天飞机高压氧涡轮泵的流体激振问题[1]，因其独特的阻尼特性，可明显提高旋转机械转子系统的稳定性，此后在透平机械中得到大量应用。ZEIDAN等[2]介绍了在背靠背和直通型2种离心压缩机平衡盘密封处改造蜂窝密封，从而成功解决压缩机失稳问题的案例。JAY和FRANCK[3]介绍了蜂窝密封成功应用于解决汽轮机次同步振动的案例。NORONHA等[4]介绍了蜂窝组合式密封应用于一台高压直通压缩机中解决振动的问题。

蜂窝密封动特性的快速准确计算是保障转子稳定性预测的关键基础，目前蜂窝密封动力特性的研究方法主要包括数值方法和实验方法。实验方法[5-7]成本较高，耗时较长。数值方法中传统的单控体[8]和双控体模型[9-10]虽然计算效率高，但在结构和工况复杂情况下误差较大[11]，均不适合快速工程应用。随着CFD技术发展，近年来国内外学者开始采用该方法研究密封动特性，并形成了一套比较成熟的理论和计算方法。国外学者MOORE[12]给出了偏心稳态计算模型，其计算方法简便，但适用面窄；CHOCHUA和SOULAS[13]提出了基于动网格技术的单频涡动模型，可计算单个涡动频率下的动特性系数。国内学者李军团队[14-15]和孙丹团队[16-17]研究了多频椭圆涡动模型，通过少量计算可获得多个频率下的转子动力特性系数，且计算精度高，对复杂结构和运行工况有良好的适应性。但关于蜂窝密封及转子稳定性的研究较少。

本文作者从蜂窝密封动特性分析入手，采用CFD非定常动网格技术和多频涡动求解模型，研究了蜂窝密封动特性系数，并与同条件下的迷宫密封进行对比，分析了蜂窝密封在实际压缩机转子上的稳定性效果。研究成果为蜂窝密封工程应用提供了依据。

1 密封动力特性理论求解模型

1.1 密封气流力线性化模型

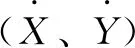
(1)

式中：K为直接刚度；k为交叉刚度；C为直接阻尼；c为交叉阻尼。

其中交叉刚度为转子失稳力的主要来源，该值越大，转子稳定性越差。

1.2 转子多频椭圆涡动模型

为求解8个动力特性系数，需要在转子上施加2组涡动激励，多频椭圆涡动激励方程[17]为

(2)

式中：Ωi为转子涡动频率；a、b为转子涡动幅值；N为转子涡动所包含的频率数。

将式(2)进行快速傅里叶变换(FFT)，可得频域内气流激振力与动力特性系数和小扰动量的关系式为

(3)

通过求解式(3)可得：

(4)

(5)

则蜂窝阻尼密封动力特性系数求解公式为

K(Ω)=Re(D(jΩ))

(6)

k(Ω)=Re(E(jΩ))

(7)

(8)

(9)

为了综合反映蜂窝阻尼密封对转子稳定性的影响，定义有效刚度和有效阻尼：

Keff=K+Ω·c

(10)

Ceff=C-k/Ω

(11)

2 密封动力特性数值求解

2.1 求解模型

图1所示为蜂窝密封。文中研究的蜂窝密封结构如图2所示，蜂窝芯格关键尺寸为对边距B，蜂窝壁厚b，蜂窝孔深h。蜂窝密封的详细结构参数见表1。

图1 蜂窝密封

图2 蜂窝密封结构示意

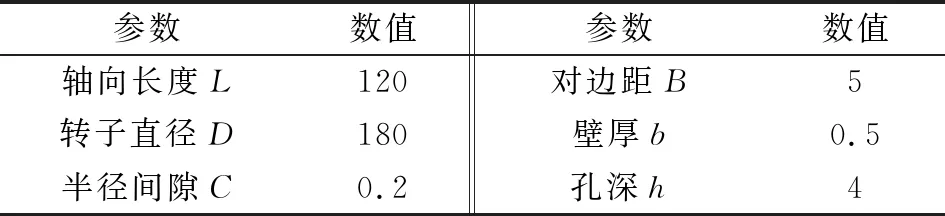
表1 蜂窝密封结构参数 单位：mm

2.2 网格划分

考虑到蜂窝密封流场结构较复杂，将密封间隙和密封腔网格分别处理。密封间隙部分由于尺寸小，流动变化大，对其径向网格进行加密处理，保障网格密度。整体网格为360°全三维结构化网格，经网格无关性验证后，单元数量控制在300万。图3所示为蜂窝密封网格示意。

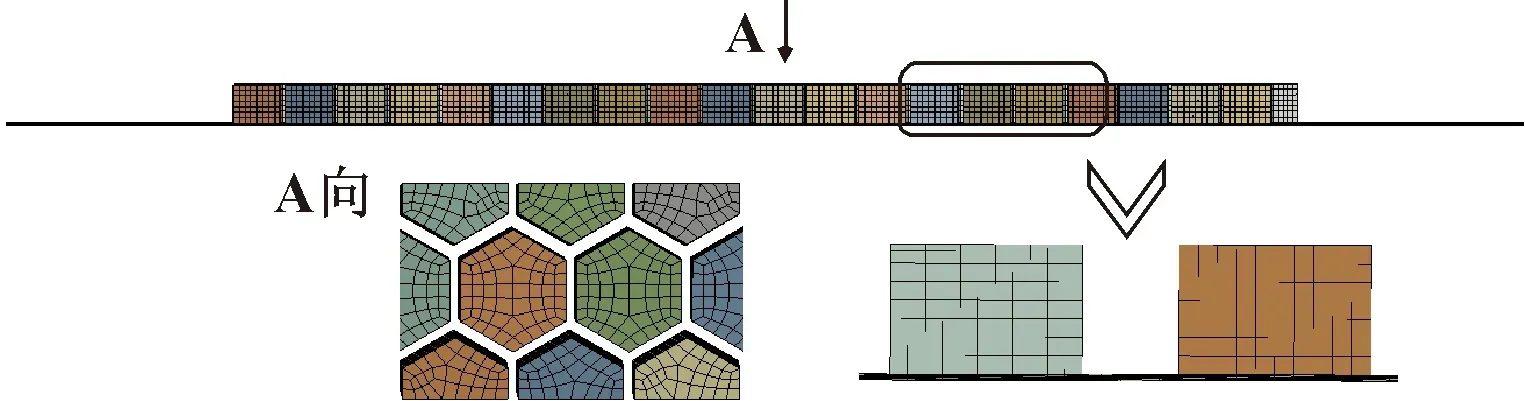
图3 蜂窝密封网格示意

2.3 载荷和边界条件

文中蜂窝密封计算域流体为理想空气，进出口边界为压力边界，转子外表面为旋转壁面，蜂窝腔室壁为静子面，设为无滑移固体壁面。图4所示为密封模型的边界条件示意，表2给出了密封计算工况。

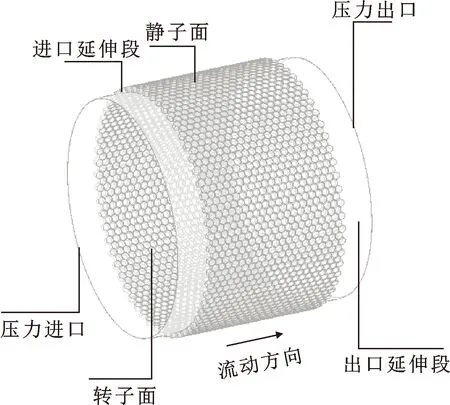
图4 蜂窝密封计算模型

表2 密封运行工况

采用多频涡动模型，选取基频40 Hz，频率个数N=7，求解涡动频率f在40、80、120、160、200、240、280 Hz下的密封动特性系数。为使涡动满足小位移涡动理论，文中将转子涡动振幅取为a=0.01C，b=0.005C，C为密封半径间隙。计算时间步长0.000 1 s。

3 计算结果及分析

3.1 涡动位移与气流力分析

图5和图6分别给出了CFD计算得出的转子面涡动位移(Y方向激励)时域图和经过快速傅里叶变换后得到的位移频域图。图7和图8分别给出了密封气流力时域图和经过快速傅里叶变换后的气流力频域图(Y方向激励)。

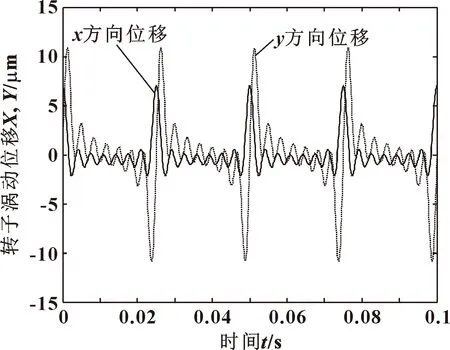
图5 转子涡动位移时域

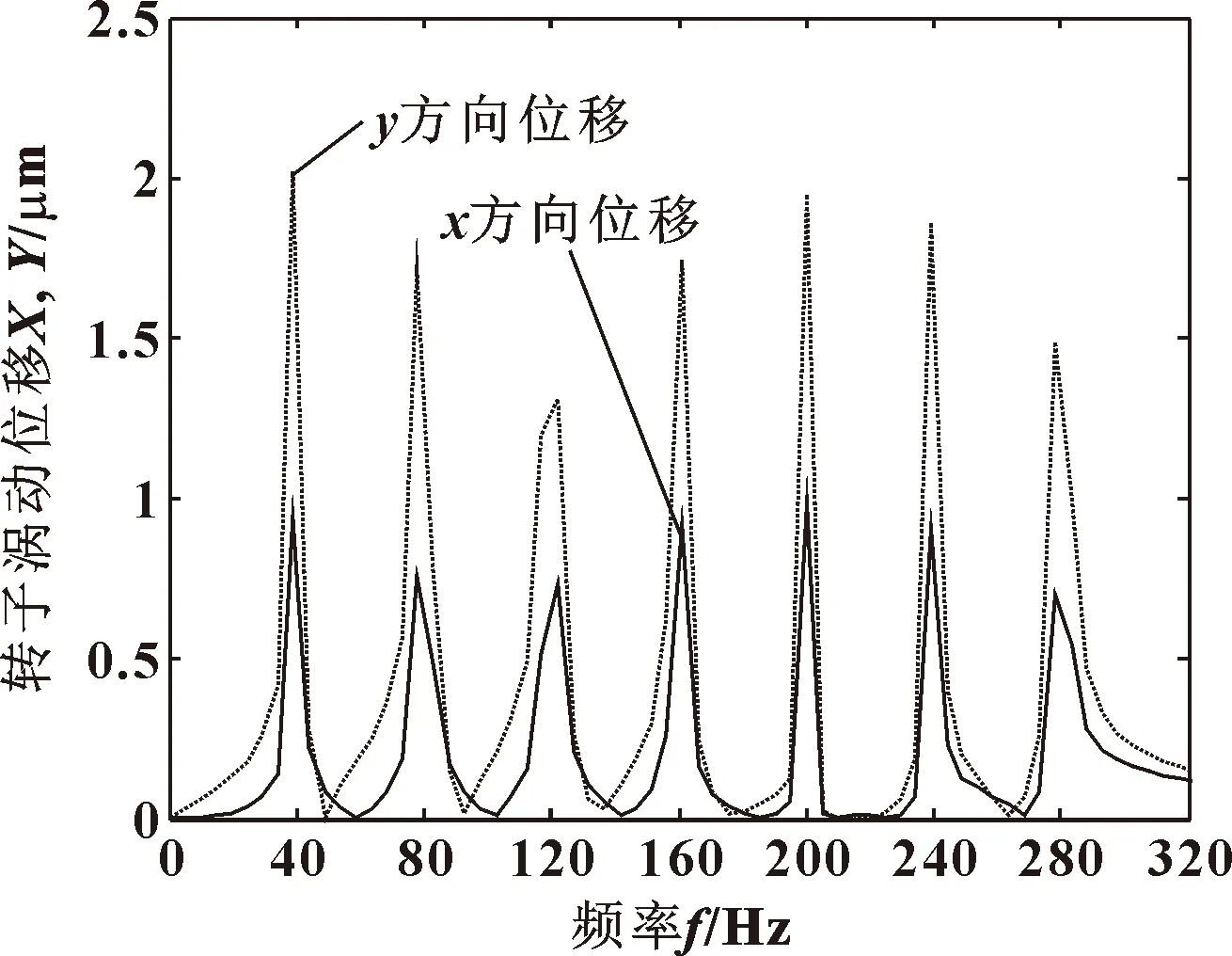
图6 转子涡动位移频域

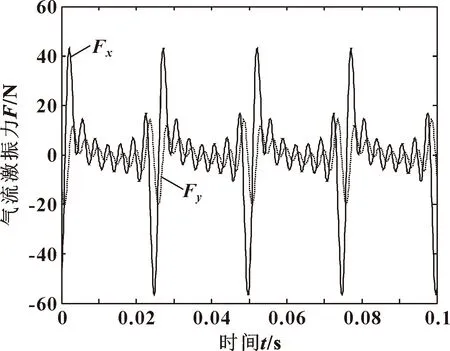
图7 气流激振力时域

由图6所示的位移频域图可看出，在一些频率处，涡动幅值与公式设定值有偏差，考虑是动网格变形和FFT计算误差引起。因此，密封动特性系数求解中，不能采用公式计算获得的涡动位移，而应采用CFD计算获得的实际涡动位移。

由图8所示的气流激振力频域图可以看出，密封气流力对应的频率成分与施加在转子上的涡动频率相同，证明多频法可准确捕捉对应涡动频率下的气流力。

图8 气流激振力频域

随着转子涡动频率的增加，在同一涡动幅值下，x方向和y方向的气流力均随涡动频率的增加而增大。

3.2 蜂窝密封动力特性分析

蜂窝密封和迷宫密封模型动力特性系数随频率的变化曲线如图9所示。可以看出，转子涡动频率对蜂窝密封动力特性系数影响较大。在工况范围内，随着频率的增加，蜂窝密封的直接刚度系数随之增加，交叉刚度和直接阻尼均减小，交叉阻尼系数呈上升趋势；有效阻尼系数随涡动频率增加而减小，有效刚度系数随涡动频率增加而增加。

如图9所示，转子涡动频率对迷宫密封动力特性系数影响不是十分明显，除迷宫密封主刚度随涡动频率增加呈现绝对值增大之外，其余参数变化较小。

图9 蜂窝密封与迷宫密封动力特性系数随涡动频率的变化

对比蜂窝密封和迷宫密封动特性参数结果可知，蜂窝密封的直接刚度系数、直接阻尼系数和交叉刚度系数均明显大于迷宫密封；在低频率区(f<80 Hz)，蜂窝阻尼密封的有效阻尼系数是迷宫密封的10倍以上，可极大增加涡动阻力，增强转子稳定性。

4 蜂窝密封转子稳定性分析

针对某型高压空气离心压缩机机组，进行蜂窝密封结构设计。转子模型如图10所示，图中B1处为轴承，序号1-7为口圈密封，序号8为平衡盘密封。机组转子总长1 800 mm，跨距1 200 mm，额定转速10 500 r/min，进口压力11 MPa，出口压力20 MPa。机组平衡盘密封直径200 mm，轴向长度90 mm。

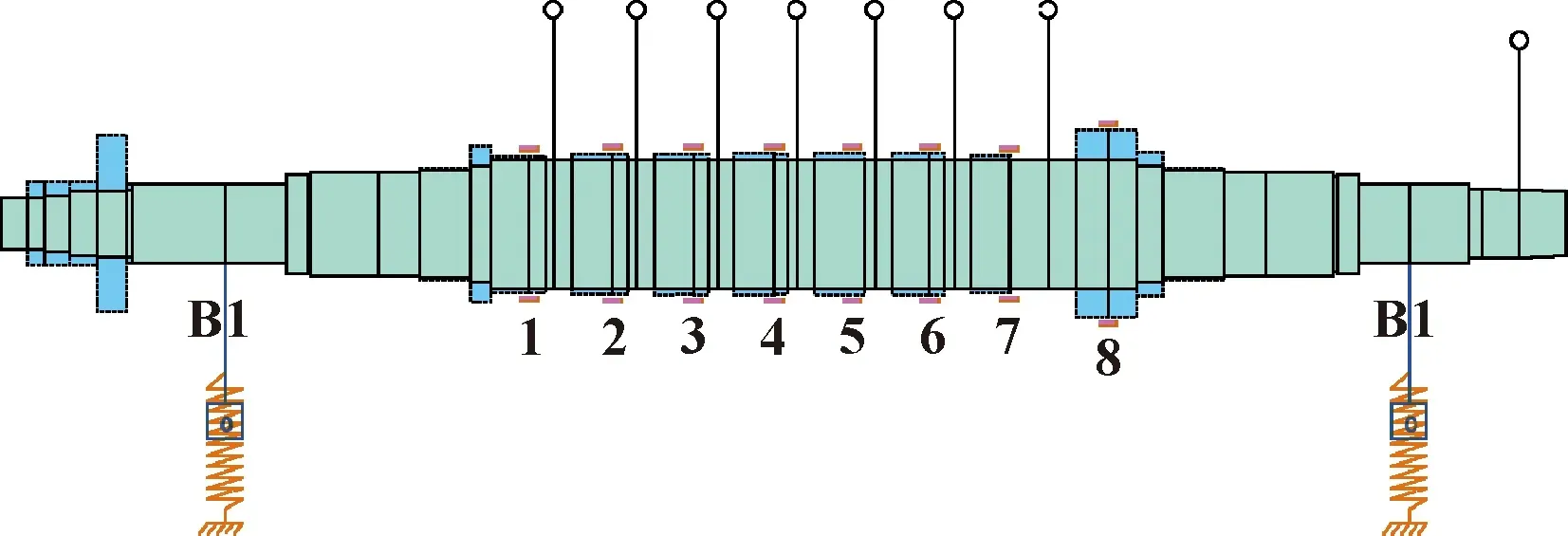
图10 离心压缩机组转子模型

对平衡盘密封处进行蜂窝阻尼密封结构设计，采用前述CFD方法对蜂窝密封动特性参数进行计算，同参数下迷宫密封和蜂窝密封的动特性参数如表3所示。可看出，相比于迷宫密封结构，平衡盘应用蜂窝密封后，密封主阻尼大幅上升，虽然交叉刚度高于迷宫密封，但蜂窝密封的有效阻尼实现了大幅提升。

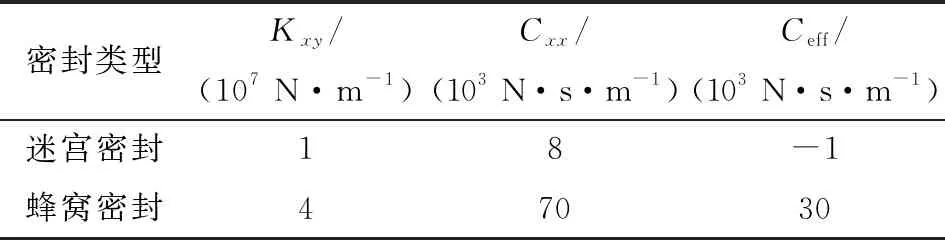
表3 密封动特性参数对比

对不同机组布置形式下的转子系统进行动力稳定性分析，结果如表4所示。可以看出，在考虑密封动力特性参数后，转子系统的动力稳定性都有降低，尤其是平衡盘密封采用常规迷宫密封设计时，转子系统的对数衰减率为-0.02，远低于行业通用标准的要求，而采用蜂窝密封的转子动力系统稳定性明显更优。

表4 转子稳定性分析结果

采用常规迷宫密封设计时，实际机组在开车运行后，随着压力负荷提高，转子系统表现出明显的密封激振导致转子失稳现象，无法达到额定设计工况点运行。将平衡盘密封由原来的迷宫型变为蜂窝密封后，通过机组现场的运行检验，机组各项运行指标完全达到设计要求，转子系统动力稳定性得到明显改善。

5 结论

(1)蜂窝密封动力特性系数随转子涡动频率变化比较明显，直接刚度系数和交叉阻尼系数随涡动频率增大而增大，交叉刚度和直接阻尼系数随涡动频率增大而减小。而迷宫密封动特性系数随涡动频率变化特征不明显，仅主刚度绝对值随频率增加而增大，其余参数变化较小。

(2)不同涡动频率下，蜂窝密封的直接刚度系数、直接阻尼系数和交叉刚度系数均明显大于迷宫密封，交叉阻尼系数小于迷宫密封；此外，有效阻尼系数高于迷宫密封，特别在低频率区，蜂窝阻尼密封的有效阻尼系数是迷宫密封的10倍以上。

(3)蜂窝密封在实际压缩机转子上的应用表明，相比传统迷宫密封，蜂窝密封能够显著提升转子对数衰减率，增加转子动力稳定性，解决密封激振导致的机组振动问题。