要素错配：解开资源型城市转型困境之谜

刘小玲，唐卓伟，孙晓华，于润群，3

（1.大连海事大学航运经济与管理学院，辽宁 大连 116024；2.大连理工大学经济管理学院，辽宁 大连 116024；3.大连交通大学经济管理学院，辽宁 大连 116028）

资源型城市是中国重要的能源与原材料供应基地，是中国国民经济持续快速增长的坚实后盾。资源型城市立足自身资源禀赋，逐步形成了以矿产能源开采加工为主体的重型产业结构，在城市建设初期有力地推动了经济的发展。然而中国资源型城市的建设受计划经济影响较深，且资源型产业本身具备自然垄断特性，因此资源型城市普遍市场化水平较低，存在着行政干预力量较大、要素配置扭曲等问题。而资源型城市过往的发展高度依赖资源型产业，随着资源持续开采面临枯竭，如果接续产业因生产要素配置不足而导致培育受阻，则资源型城市后续发展空间十分有限。这些城市在早期开发过程中，缺乏环保意识与可持续发展意识，生态环境遭到严重破坏，资源能源的开采利用和粗加工也伴随着高能耗和大量的碳排放，城市转型面临巨大的挑战和困难。在中国不断优化能源消费结构、实现碳达峰碳中和目标的新形势下，资源型城市如何实现产业转型是中国实现高质量可持续发展必须要面对的重要问题，而寻找造成资源诅咒困境的内在原因，成为新时期推进资源型城市产业转型和实现区域协调发展的关键。

1 文献综述

国内外关于资源型城市经济转型问题的研究较为丰富。学术界的研究主要集中在资源型城市转型问题形成原因［1-2］、转型发展阶段［3-5］及转型困难［6-7］等，并总结了资源型城市转型经验［8-9］以及如何进行产业升级［10-12］等建议。随着中国工业化和城镇化的进程不断深化，中国资源型城市的“资源诅咒”现象开始显现，学者们对此进行了大量而深入的探讨。杨继瑞等［13］认为资源型城市之所以面临发展困境在于其过分依靠自然资源开采，并养成了粗加工单一经济结构的产业路径依赖。冯宗宪等［14］指出中国“荷兰病”的现象比较普遍，繁荣的资源型产业会过度占有资本和劳动力，抬高要素使用成本，经实证发现资源产业对制造业的固定资产投资具有明显的挤出效应，但对劳动力的供给基本没有影响。

面对中国资源型城市转型的种种问题和现状，不同学者已提出大量解决方案。孙毅等［15］指出产业绿色转型和经济发展方式绿色转变是资源型城市实现经济发展与生态环境保护双赢的必由之路，徐君等［16］构建了低碳化的战略框架并提出生态文明视域下资源型城市低碳转型的路径，杨丹辉等［17］指出要通过绿色化、智能化转型，推动资源型产业与非资源型产业融合发展。针对资源型城市为实现转型而做的各种尝试及其效果，学者们也设计出各种指标体系进行定量评价。白雪洁等［18］采用坏产出动态SBM模型测算了资源衰退型城市的转型效率，并进一步定量地刻画了其减排空间、节能潜力，并指出外资流量、科教支持有助于城市转型；李汝资等［19］利用有隶属函数性质的分段函数模型将资源型城市转型的不同阶段进行划分，并构建起基于转型阶段的指标体系评价转型效果，发现在综合考察城市经济与社会发展、基础设施建设、环境污染治理等方面后，石油类资源型城市转型效果更优。

从要素错配的视角出发，研究地区间发展水平差异是学术界近年研究的热点。Hsieh等［20］指出，要素市场扭曲会对全要素生产率产生影响，而全要素生产率又决定着人均产出和国家总体产出水平［21］。Restuccia等［22］从企业视角出发，发现企业资源错配会影响其自身生产率，而正是企业间的生产率差异造成了国与国之间的产出差异。从对中国问题的经验研究来看，中国要素错配的现象十分普遍。龚关等［23］测算了中国制造业的资源配置效率，发现如果资本和劳动要素得到有效的配置，中国制造业的全要素生产率可大幅提高。马颖等［24］认为，中国行业间的人力资本错配使行业实际产出低于最优产出，阻碍了中国经济总产出的提高。张杰等［25］指出要素市场扭曲对中国企业R＆D投入具有明显的抑制效应，要素市场扭曲会同时抑制本土和外资企业的R＆D投入。阚大学等［26］采用空间动态面板模型，研究发现要素市场扭曲加剧了环境污染，且环境污染存在空间溢出效应，同时要素扭曲对劳动和资本密集型行业影响较大，容易加剧其污染。林伯强等［27］指出要素扭曲可通过锁定粗放增长模式、鼓励寻租、限制地区间专业化分工等途径来阻碍中国能源效率的提升。

在现有文献中，有关资源型城市转型的研究多从产业角度理解发展困难，将分析重点落在转型方案的设计上，鲜有文献从要素错配视角破题，从理论上系统阐释资源型城市形成转型困境的原因。而有关要素错配的文献一般从经济整体或者三次产业等角度考察要素错配问题，较少从细分行业层面探讨要素错配对经济效率的作用。与现有研究不同，该研究将要素错配和效率损失的讨论纳入到增长核算框架，建立一个测算多行业间要素错配的理论模型，在度量要素错配和经济效率的基础上，实证检验资源型城市要素错配对产业转型的影响。该研究的边际贡献体现在两个方面：①从经济产出、能源消耗和污染排放三个维度，丰富了资源型城市产业转型的内涵，利用改进后的方向距离函数测算了资源型城市的产业转型效率，并进一步分解为产出效率、能源效率和环境效率。②将能源要素纳入到生产函数中，构建了旨在分析要素错配对地区生产效率影响的理论模型，不仅从投入端分析要素错配程度，而且从行业层面出发推导出要素错配影响整体转型的过程，破解资源型城市的转型困境。

2 模型构建

该部分旨在构建一个含有要素错配的多行业增长模型，用以说明要素错配在产出损失、能源消耗以及环境保护等方面如何影响资源型城市转型。Syrquin［28］的研究最早将全要素生产率TFP的增长分解为两部分，一部分来自行业TFP的增长，一部分来自要素的配置效应，而Aoki［29］进一步考察了行业间的要素错配，利用完全竞争模型，使用劳动和资本税收来刻画资本配置的扭曲程度。因此该研究将Aoki等［29］和陈永伟等［30］分析框架结合起来，将其构造为一个探讨资源型城市多行业中要素错配如何影响行业与经济总产出的理论框架。

2.1 基本设定

假设同一个行业内所有企业均拥有相同的生产函数，这样可将行业的生产问题简化为一个代表性企业的生产问题，而不同行业间则假定拥有相异的生产函数。资本K、劳动力L、能源E三要素是各企业进行生产所必需的三种要素，并且市场中的所有企业均是价格接受者，接受市场给定的价格。参考Hsieh等［20］的做法，行业i中的企业均被给定一个扭曲的价格，且扭曲具体表现为从价税：资本的价格为（1+τKi）pK，劳动力的价格为（1+τLi）pL，能源的价格为（1+τEi）pE，其中pK、pL、pE是完全竞争条件下不存在要素配置扭曲时的资本、劳动、能源要素对应的价格，τKi、τLi、τEi分别表示i行业中企业所面临的各要素扭曲“税”。

假设i行业代表性企业具有Cobb-Douglas型的生产函数，故行业i的代表性企业生产函数为：

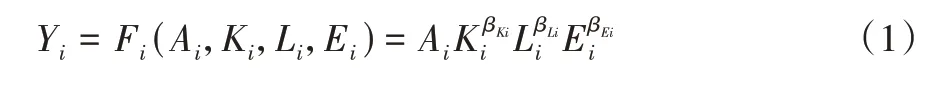
其中：Yi表示产出，Ki、Li、Ei分别表示投入的资本、劳动和能源的量。参数βKi、βLi、βEi分别表示三类要素对产出的贡献比例。假设βKi+βLi+βEi=1，即生产函数具有规模报酬不变的性质。

在假设产品市场价格不存在扭曲、各要素都是外生给定的条件下，企业的利润函数为：

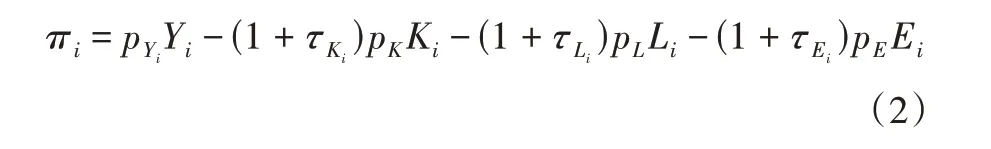
其中：pYi是行业i的产品价格。则利润最大化的一阶条件为：

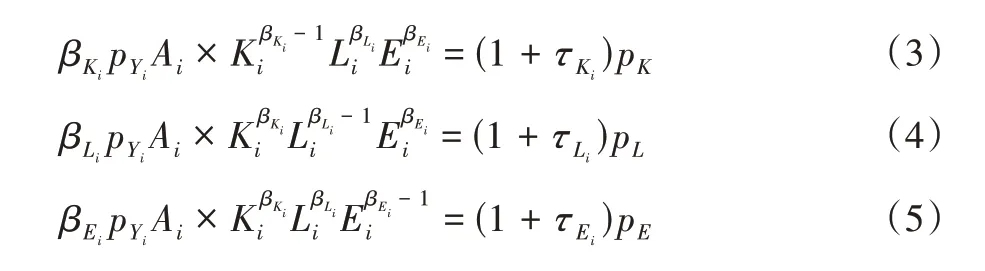
假定各行业所生产的产量价格为1，其决定了可被计价表示的全社会经济总产量Y，表达式为

根据前文假设，F（·）满足规模报酬不变，故

由欧拉定理可得，社会各个行业的产值直接加总等于全部经济产值，即

假设在每个考察期内，资本、劳动、能源等要素的投入量为定值且外生，故而资源约束条件的表达式如下：

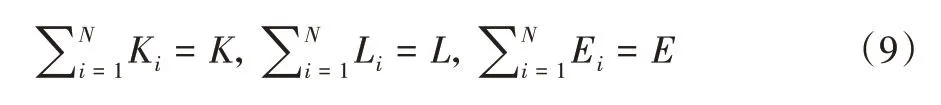
在达到竞争均衡时，任一行业i的产出总值与全社会总产值之比表示为其所占份额，即si=piYi/Y，再考虑其加权后的要素贡献值为在考虑要素配置扭曲的多部门竞争时，均衡条件下行业K、L和E的相对扭曲系数可表示成：

该研究通过式（10）、式（11）和式（12）表现要素价格扭曲系数，并将要素使用成本扭曲和要素错配联系起来。以资本为例，式（10）中分子Ki K为实际资本投入额占总资本投入额的比例，分母则表示资本实现有效配置时资本投入额的理论占比，两者的比值即为资本错配的程度。

2.2 要素错配对产出效率的影响

在实现竞争均衡后，进一步构建产出和要素价格扭曲两者间的联系。由式（1）和式（10）、式（11）和式（12）式可知，在竞争均衡下行业i的产出可表示为

取对数变形，有

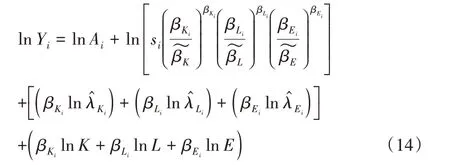
其中：行业i的产出水平既取决于要素使用数量及行业生产率，也和该行业要素使用成本的扭曲情况紧密相关。因此当保持要素数量及行业生产率既定时，要素使用成本的扭曲状况发生任何改变都将直接影响产出水平。在此基础上，将进一步讨论该效应。

2.2.1 产出的分解

由于前文已经对要素价格的相对扭曲进行了设定和推导，因此对要素配置效应继续分解，即配置效应包括仅仅份额变动带来的贡献和要素价格扭曲变动的贡献。

在具体推导中，假定整个经济在任意一期都实现了均衡，则经济从t期到t+1期总产值的变动差值为ΔlnYt=lnYt+1-lnYt，其中，Δ是差分算子，即Δxt=xt+1-xt，则ΔlnYt可以分解为：

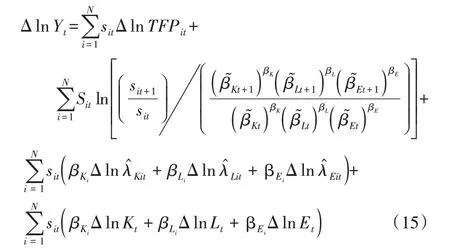
有别于Syrquin的初始核算框架，要素的配置效应可以分解为第二、三项两个部分。具体来看，第二项是仅仅产出份额变动带来的变化，它的经济学含义是要素在各行业间的重新配置对于“加总技术”的影响。第三项是各行业要素价格扭曲程度变动所引起变化。带有扭曲的价格使要素不能最优地配置在行业间，因此只要价格的扭曲程度下降，要素就会重新流动以趋近最优配置，进而提升TFP和经济总产值。此外，由于前文已经设定了生产函数为Cobb-Douglas加总生产函数，因此第三项的另一种解释为产出缺口的变动，后续会进行说明。

2.2.2 产出缺口的估计

产出缺口，即实际产出和资源有效配置（不存在要素配置扭曲）时产出之间的缺口。利用加总的C-D函数，可以将产出缺口表示为各行业资源相对扭曲系数的函数。实际产出与有效产出之间的比值可以表示为各行业资源扭曲系数的函数，即

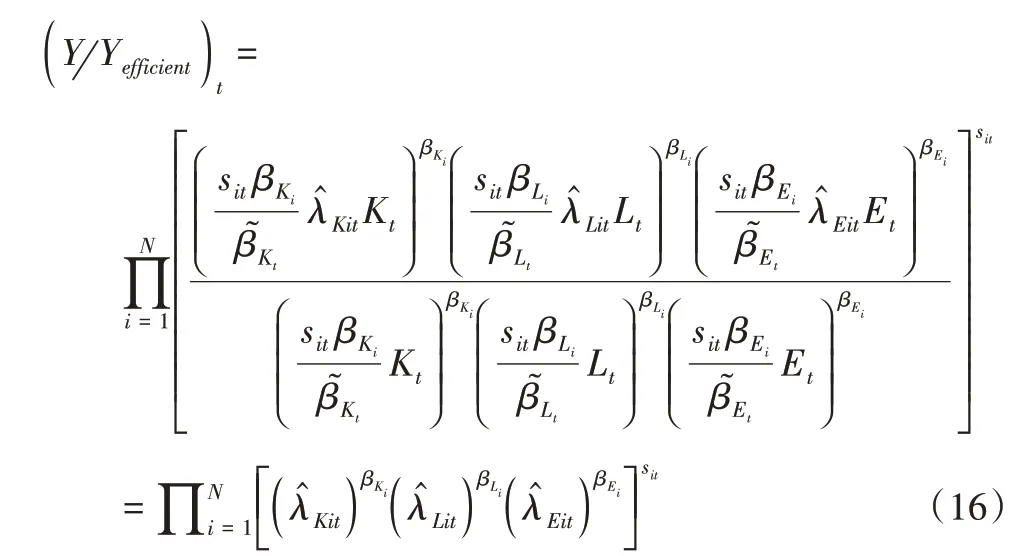
其中：Yefficient表示理想状态下的经济总产出，(Y Yefficient)t表示t时期实际经济产出与无要素扭曲配置下的理想产出之比。假设各行业在整个工业中的相对产出比例sit不变，则在t+1时期类似可得

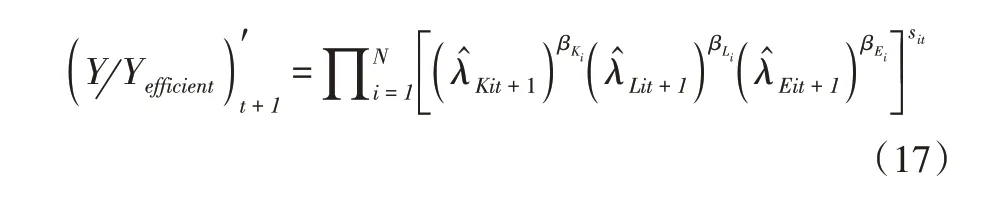
从而，

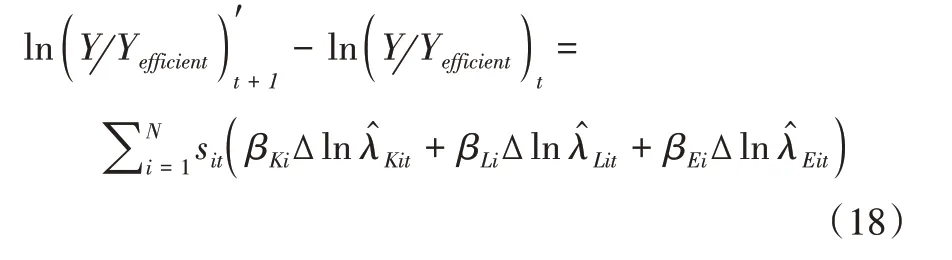
等式右边为式（15）中的第三项。根据式（18）可以得到一些直观解释：以资本要素为例，考虑保持其他条件不变，仅让行业i的资本扭曲“税”τKi下降，则根据定义，Δlnλ^Ki＞0。由于扭曲“税”的减少，行业i使用资本的成本下降，而成本的降低会鼓励行业增加对资本的占有以扩大生产，由（15）式可得该直接作用的大小约为sit βKiΔlnλ^Ki。而扭曲税的减少也会产生外部性，让剩余行业使用资本的成本变相增加，进而迫使其他行业减少资本使用，缩减产量。由此可得命题1。

命题1：在其他条件相同的情况下，要素错配越严重，资源型城市产出损失越多，产出效率越低。

2.3 要素错配对能源效率的影响

能源等资源的开发利用不仅带来了经济增长，同时也伴随着环境污染等非期望产出，因此能源使用效率的高低或单位能源的产出量大小不仅关乎经济效率，也对环境问题有着巨大影响。该部分在借鉴已有研究基础上［31］，尝试提出一个分析框架，旨在研究行业间要素错配通过何种方式影响能源效率，进而间接对环境产生影响。仍沿用前文C-D生产函数，但简化为两行业的生产函数，一个行业具有高技术低能耗的生产特点，一个具有低技术高能耗的生产特点，行业中的企业均为价格接受者。

定义行业代表性企业生产函数为：

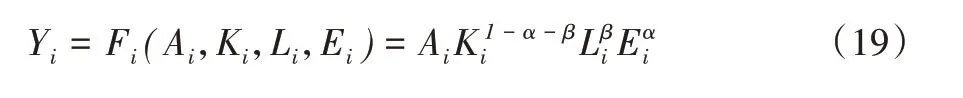
假设产品市场的价格不存在扭曲，企业的利润函数为：

其中：pY是产品价格，pY是外生给定的，能源要素的市场价格为p、资本的价格为r，劳动的价格为w。对利润函数求一阶条件得到能源要素需求函数：

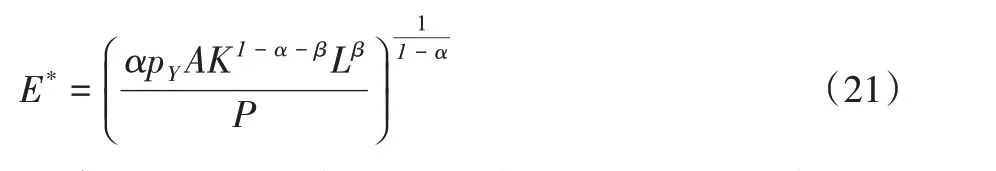
构建一个能源效率函数，在任一期内劳动要素总量L、资本要素总量K及能源要素总量E均为外生给定，经济体能源效率达到最优时的能源配置为下式：

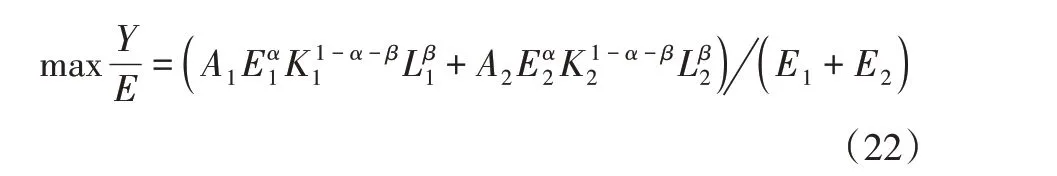
结合E1、E2的约束条件，利用拉格朗日乘数法，可得：

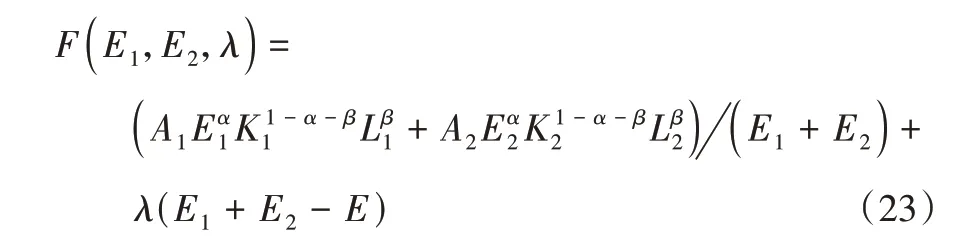
对E1、E2求偏导并联立，可得

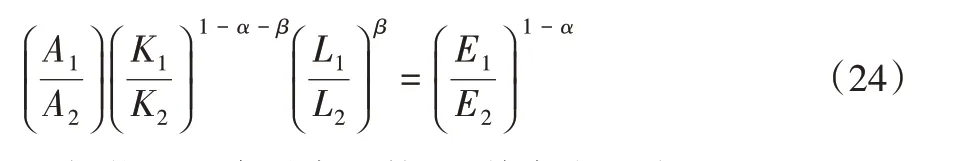
根据能源要素需求函数，对其求全微分可得：

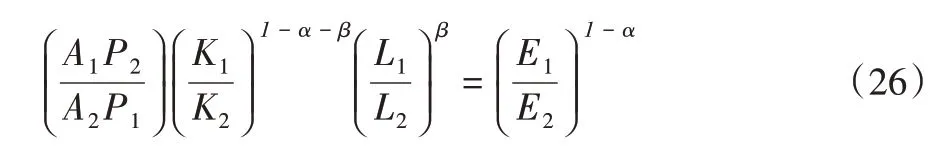
能源要素的错配主要由能源价格扭曲引起，如果假设能源市场是一个完全竞争市场，那么两行业将面临相同的市场价格（即P1=P2），从而式（26）会变为式（24），即市场机制下的能源要素配置是有效率的，满足经济体能源效率最优条件，技术水平与能源要素占有水平成正比，即低能耗高技术的企业应该占有更多能源要素。但是，当能源要素价格存在扭曲时，换言之两个行业面临不同的市场价格（P1≠P2）时，式（26）和式（24）将并不相同，即两个行业达到均衡状态时要素配置将不同于效率最优条件下的配置。以P1＞P2情况为例，即高能耗企业占有了低价能源要素，使E1≤E2的情况实现，这和式（24）效率最优状态相悖，造成整体能源效率损失。由此可得：

命题2：在其他条件相同的情况下，要素错配越严重，资源型城市能源效率越低，环境效率越低，总体转型效率也越低。

3 实证研究设计

3.1 计量模型

根据前文的模型构建和研究假设，该部分构建下面的计量经济方程：

其中：tranfit表示资源型城市的转型效率；DisKit，DisLit，DisEit代表要素错配程度，分别为资源型城市i在t年的资本、劳动和能源的错配程度；Xit是控制变量集合，包括城市的对外开放、汽车保有量、政府干预程度、产业结构以及研发投入水平等变量；μi和νt分别表示城市固定效应和年份固定效应；下标i表示城市，t表示年份。α1、α2、α3是该研究的关注重点，刻画了要素错配程度对资源型城市转型效率的影响。若其显著为负，则说明要素错配程度的提高阻碍了资源型城市的转型；反之则说明提高要素错配程度有利于资源型城市的转型。为了进一步考察要素错配方向对资源型城市转型效率的影响，式（28）中引入要素错配程度与要素错配方向的交互项，其中Dircetit表示资源型城市i在t年某一要素的错配方向，Discit表示某一种要素的错配程度。式（29）中的解释变量纳入了城市转型效率的滞后一期项和滞后二期项，采用与式（27）及式（28）回归方法不同的动态面板模型进行回归估计以缓解内生性问题。

3.2 变量设定

该研究的被解释变量是资源型城市的转型效率。资源型城市的经济转型关键在于产业结构的转型，由以资源产业为主导向培育第三产业、高技术产业以及新兴产业等替代产业方向转变。在这一过程中，通过要素的合理配置实现产业结构升级，进而实现经济、能源、生态等可持续发展的经济发展方式的转变。因此，资源型城市要想实现转型升级与“高质量绿色”增长，必然包含三个基本维度：附加值增长、节约能源和降低污染［32］。该研究将中国每个地级市看作一个复杂的投入产出系统，在考虑能源和环境的因素下评价各地级市在经济转型升级过程中的投入产出效率，即以最小的资本、劳动和能源投入实现最快的经济增长和环境友好，在节能减排的目标下保持经济的稳定增长，因此将城市的投入产出效率界定为转型效率［13］。该研究将借鉴孙晓华等［33］的计算方法，利用改进后的方向距离函数（DDF）［34-35］，分别从劳动、资本和能源投入以及期望产出和非期望产出五个维度对各资源型城市的转型效率进行测算。

该研究在投入要素方面除了劳动和资本投入之外，特别选取了能源投入量，以考察各城市对能源的利用效率。在产出方面，选取污染排放指标作为非期望产出，以GDP作为期望产出。变量选择过程具体如下：

在劳动投入方面，该研究选择各城市职工平均在岗人数作为劳动投入；资本投入方面，该研究选择固定资产投资作为资本投入，并采用以往文献较为常用的永续盘存法估算实际资本存量［36］；能源投入方面，该研究选取工业用电量作为衡量指标［37-39］。

在期望产出方面，该研究拟用实际GDP来衡量城市是否实现经济增长的转型目标，通过对历年名义GDP进行平减可得实际GDP。对于非期望产出，主要考虑工业生产过程中的非期望产出，包括土地污染、水污染、重金属污染、固体废弃物污染、大气污染等。因为缺乏数据无法对重金属污染和土地污染进行量化，该研究将选用工业废水、工业二氧化硫和工业烟尘三种污染排放物的排放量作为非期望产出。通过熵值法将“工业三废”进行无量纲化的处理，分别计算出各个年份每种污染物的权重系数，并根据各年之间三种污染物的数值比例，得到以2003年为基期历年各城市可比量的综合污染排放指数。该研究使用MATLAB软件进行编程和运算，参考王昀等［32］和孙晓华等［33］的做法，分别在（1/9，1/9，1/9，1/3，1/3）和（0，0，1/3，1/3，1/3）两种权重设定下，得到中国各资源型城市2003—2018年的转型效率tranf和trane。其中，第一种权重表示投入、期望产出和非期望产出三者间有着相同的重要程度，故各自权重为1/3；而投入中三类要素同等重要，故进一步分解为1/9。第二种权重表示能源投入、期望产出与非期望产出有同等重要性，重点考察目标为能源投入与环境产出效率，资本和劳动投入为非考察对象，不占权重。在测算转型效率（tranf和trane）的框架基础上，固定劳动和资本要素投入，将DDF方法计算出的前沿面的方向向量分别投影到能源消耗、GDP和污染排放方向上，对应着在能源节约、经济增长和环境友好三个方向上将其进一步分解得到相应效率，即从能源效率（e），产出效率（y）和环境效率（env）三个方面分别考察资源型城市是如何受要素错配影响的。

该研究的核心解释变量是资源型城市的要素错配程度，具体为三种指标：Disk、Disl、Dise，其分别表示资本要素错配程度、劳动要素错配程度和能源要素错配程度。在理想的完全竞争市场中，要素可以无摩擦地自由流动、配置，要素价格与要素的边际产品价值相等；而由于市场不完善或其他非市场因素干预了要素价格确定，要素价格偏离要素的边际产品价值，而市场难以自我调节，则要素配置无法实现完全竞争下的最优状态，产生效率损失，此时就出现了要素错配。为测度错配程度，本部分利用前文的C-D生产函数，结合式（10）、式（11）、式（12），依据Aoki［24］的核算框架测算要素错配系数，将其减1再取绝对值即可得到要素错配程度。要素错配方向为虚拟变量，三种要素错配方向对应的指标为dk，dl和de，将要素错配系数与1进行比较以得到具体的要素错配方向：系数小于1为要素配置不足，分别记为dk1，dl1和de1；系数大于1为要素配置过度，分别记为dk2，dl2和de2。

为了控制其他因素对城市转型效率的影响，借鉴已有的理论和文献［40-42］，主要控制变量设置如下。

政府干预（dis）：地方政府可以影响环境保护等公共产品的供给，并通过财政手段能在一定程度上影响城市经济结构的变动。该研究采用扣除教育和科学事业支出后的财政支出占地区生产总值的比重来衡量政府干预程度。

贸易依存（trade）：对外贸易有助于促进城市的经济增长，因此采用进出口贸易总额与城市的地区生产总值作为代理变量。

汽车保有量（car）：城市中日益增多的汽车会产生大量尾气，成为空气的重要污染源之一，同时也消耗着大量的石油资源，对城市环保和能耗有着直接的影响。该研究直接使用各个城市的民用汽车保有量来刻画该变量。

产业结构（ind）：在三次产业结构中，资源型城市的工业尤其是采矿业往往会被优先发展，这为资源型城市带来经济增长的同时也不可避免地消耗大量能源、产生大量污染，因此资源型城市的转型离不开产业结构的调整升级。因此该研究使用采矿业与劳动力就业人数之比当作产业结构的代理变量。

研发投入（rd）：研发投入高的城市往往创新能力更强，由此产生的科技进步能带来更高效环保的技术，进而促进资源型城市顺利地转型升级。该研究以科学研究、技术服务和地质勘査业与劳动力就业人数之比来衡量研发投入。

3.3 数据来源

3.3.1 数据来源及说明

该研究选取2005—2018年中国114个资源型城市的面板数据，来研究要素错配对资源型城市转型升级的影响。根据《全国资源型城市可持续发展规划（2013—2020年）》（下称《规划》）对资源型城市的界定，全国共有262个资源型城市，其中地级行政区126个。由于县级市、县以及市辖区在级别、经济规模、影响力等方面与地级行政区存在明显差异，因此该研究以地级行政区为研究对象。在126个地级行政区中，该研究剔除了关键数据缺失较为严重的样本，删除了考察期间发生过行政区划变动的样本，最终获得研究样本城市114个。在这114个城市中，按城市地理区位可分为东部（20个）、中部（37个）、西部（36个）和东北部（21个）四类；按《规划》中对资源型城市的划分，可分为成长型（14个）、成熟型（62个）、衰退型（23个）和再生型（15个）四类。文中原始数据来自于《中国城市统计年鉴》《中国区域经济统计年鉴》和各省市统计年鉴，以及各市国民经济和社会发展统计公报。

3.3.2 主要变量的描述性统计

由于统计偏差等原因，原始数据可能存在异常观测值，由此会影响到最终的回归结果。为了尽可能地降低信息损失，该研究对要素错配程度数据进行了缩尾处理，根据要素错配程度的计算特点选择在右侧90%分位处做离群值处理，对于大于90%分位的数用90%分位的值赋值，以在保留原有数据样本量的基础上避免异常值的干扰。在处理极端值之后，该研究的主要指标及其描述统计值均在表1中进行了说明。

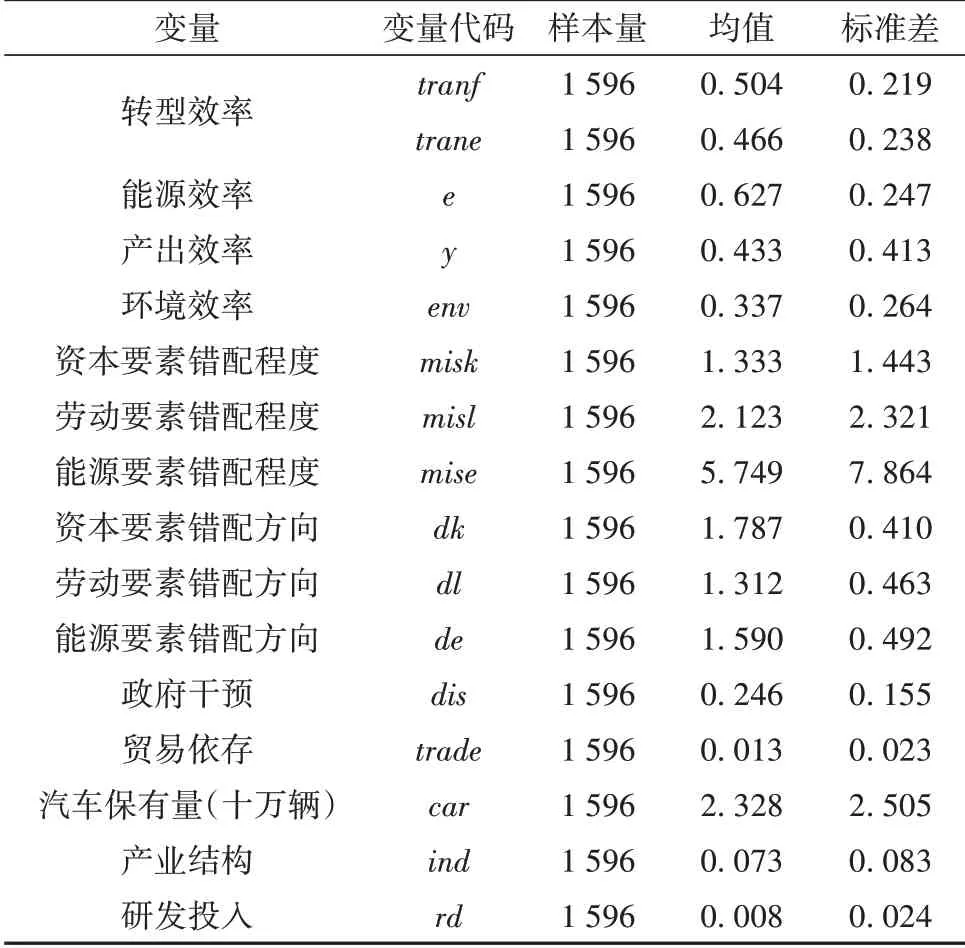
表1 主要变量的描述统计

图1展示了资源型城市不同转型效率水平的区间特征。将转型效率划分为高中低三个水平，0.3以下为低效率水平，0.3至0.7为中效率水平，0.7至1.0为高效率水平。图1显示了不同效率水平城市在总体中的占比，80%以上的资源型城市集中在中效和低效区间，且高效区的城市占比并未呈现稳步上升的趋势，说明中国资源型城市整体转型效率水平有待提高，升级空间较大。

图1 资源型城市转型效率区间分布

4 实证结果分析

4.1 基准结果

该研究以2005—2018年城市层面的面板数据为样本进行回归，得到表2所示的结果。所有列均控制了城市固定效应，列（2）、列（3）、列（5）、列（6）加入城市层面的控制变量，列（3）、列（6）控制了年份固定效应。考虑到所有指标是城市层面的，回归模型中均使用城市聚类效应对标准误进行修正。可以看出，无论是否加入控制变量，要素错配程度的系数均显著为负，分别通过1%和5%的显著性检验。这表明，在不考虑模型内生性存在的情况下，资源型城市要素错配程度与其转型效率显著负相关，即各要素错配程度越高，城市转型效率越低，要素错配对于资源型城市的转型存在明显的抑制作用。

表2 基准回归结果

在两种外生权重设定下，劳动要素错配程度对转型效率的影响均是最大的。由列（3）可知，在同时考虑资本、劳动和能源投入的转型效率上，资本错配对转型效率的影响是高于能源错配的。而列（6）表明，在只考虑能源投入的转型效率上，能源错配对资源型城市转型的影响显著提升，资本错配程度的影响系数则略微下降。以列（3）为例，城市的劳动要素错配程度每提高1个单位，城市的转型效率则平均会下降0.067，资本错配对应下降0.038，能源错配对应下降0.025。劳动要素在资源型城市转型中扮演了更重要的角色，其原因在于：能源要素对资源型产业更为重要而对其他行业影响较小，因此能源要素对全社会的产出影响较小而更多的是产生非期望产出以影响环境，对转型效率的影响更多集中在环境方面；资源型城市产业结构不合理，同样需要大量固定投资的其他制造业先天发育不足，工业内部结构单一，尽管存在资源型产业资本配置过度的现象，但是由于其他制造业体量过小，服务业对资本要素需求不大，总体来看对其他行业产出的挤出相对有限，但是资源型产业资本配置过度的确对环境有明显影响；劳动要素对各行业有较大影响，资源型城市早期的采掘业自动化水平较低，仍需雇佣大量人工进行开挖采掘，因此劳动要素的配置状况会对整个城市的产出产生直接而明显的影响，同时人力资本的积累也会影响技术水平的提高，间接地影响能效和生产效率，进而作用于产出和环境绩效。

为了探索要素错配的不同方向对城市转型效率的影响，表3报告了要素错配程度与要素错配方向虚拟变量交叉项的估计结果。可以看到，引入要素错配方向异质性的设定并没有改变回归的基本结果，要素错配估计系数的方向与显著性也基本保持一致，对资源型城市转型效率的影响仍基本显著为负。只有在资本配置不足时，要素错配的估计系数不显著，可能是在这种情况下，资本要素配置不足与配置过度的样本量相差较大、配置不足的数量较少所致，由表1可知，资本配置方向的均值1.787，大多数城市在大部分时间均是资本要素配置过度的状态。由列（2）、列（3）、列（5）、列（6）可知，在两种不同权重设定的转型效率情形下，无论是劳动要素还是能源要素，配置过度估计系数的绝对值均大于配置不足的，即要素配置过度对城市转型效率的影响大于要素配置不足对转型效率的影响。总体上，要素配置方向对城市转型效率的影响与理论预期及前文实证分析结果一致，要素错配对资源型城市转型具有抑制效应的估计结果是稳健的，具有可信度。

表3 要素错配方向与产业转型效率的回归结果

4.2 内生性问题讨论及解决

资源型城市要素错配与转型效率之间可能存在反向因果关系，即转型效率较低的资源型城市为了发展，有可能加强对某一要素的依赖，进一步加剧要素错配程度；同时，尽管该研究控制了一系列控制变量，模型仍可能存在遗漏变量问题或要素错配程度存在测量误差，因此基准模型内生性问题的存在使得上述结论可能存在偏误。针对模型的内生性问题，该部分将采用工具变量法进行回归以保持结论的稳健性：①该研究采用各要素的要素错配程度滞后一期作为工具变量，进而使用两阶段最小二乘法（2SLS）进行回归估计。该研究所构建的工具变量符合相关性和排他性两个基本原则：一方面，资源型城市自身上一期的要素错配程度与当期的错配程度存在高度相关性是显然的；另一方面，资源型城市当期的转型效率无法影响过去的要素错配程度，故要素错配程度的滞后值与误差项不相关，也满足外生性的要求。②在采用要素错配程度的滞后值作为工具变量的基础上，该研究在解释变量中纳入被解释变量城市转型效率的滞后1～2期构建动态面板模型，再利用要素错配程度滞后1～2期作为工具变量，运用系统GMM模型进行估计［43-44］。在采用两阶段最小二乘法（2SLS）进行工具变量回归时所用变量与样本与基准回归中的设定保持一致。

4.2.1 工具变量法

表4报告了以要素错配程度滞后一期作为工具变量的两阶段最小二乘法（2SLS）回归结果。第一阶段的回归结果表明，不同权重转型效率下的F统计量均远大于经验值10，要素错配程度滞后一期满足工具变量的基本要求。进一步，第二阶段回归结果显示，列（4）资本要素错配程度回归系数在5%的水平下通过检验，系数为负，其余各要素错配程度的回归系数均在1%的显著水平下为负，这表明考虑模型内生性后，各要素错配程度越高，城市转型效率越低，缓解各要素的错配程度会有助于资源型城市的转型。同时，劳动要素错配程度的回归系数绝对值仍然是最大的，而资本要素和能源要素错配程度的回归系数比较接近，这与基准回归中的结果比较接近，回归结果较为稳健。因此，在考虑要素错配和资源型城市转型之间可能存在的内生性问题后，采用工具变量法进行两阶段最小二乘法回归所得分析结论与前文一致，要素错配会显著阻碍资源型城市的转型。

表4 全样本2SLS回归估计结果

4.2.2 动态面板回归

在使用系统GMM方法进行估计时要求模型中的扰动项不存在自相关，但对扰动项进行差分后通常存在一阶自相关，因此要接受扰动项无自相关这一假设，需要保证差分后的扰动项不能存在二阶自相关，可以通过比较表5中AR2统计量P值的大小来判断有无二阶自相关；动态面板模型不仅需要检验扰动项的二阶自相关，还需要检验工具变量选取的合理性，因此表5中还展示了Sargan统计量的P值，可以用来判断动态面板模型中工具变量的选择是否合理。通过系统GMM模型的回归，具体结果见表5。无论是同时考虑资本、劳动和能源投入的转型效率还是只考虑能源投入的转型效率，AR2统计量P值均大于0.1，可以显著拒绝扰动项差分存在二阶自相关的假设，而Sargan统计量的P值均大于0.2，表明模型选取的工具变量不存在过度识别，可以接受所有工具变量都有效的假设，因此系统GMM的估计是有效的。

表5 动态面板回归估计结果

表5表明，在控制了城市层面特征变量的条件下，各要素错配程度的回归系数均为负且均在1%的水平上显著，说明在考虑模型的内生性问题后，要素错配对城市转型效率依然有显著的负向影响，与基准回归结论“要素错配对于资源型城市的转型存在明显的抑制作用”一致。进一步与基准回归的结果进行比较，在考虑内生性后，不同要素的错配程度对资源型城市转型效率的影响力大小出现变化。在系统GMM模型中，在解释变量中纳入转型效率的滞后项后，各要素错配程度的回归系数均显著变小，尤其是劳动和能源要素错配程度的回归系数变动幅度较大。以表5中同时考虑资本、劳动和能源投入的转型效率（tranf）为例，资本要素错配程度的回归系数由-0.038变化至-0.028，劳动要素错配程度的回归系数绝对值由0.067减小至0.018，能源要素错配程度的回归系数绝对值由0.025减至0.009，也导致资本要素错配对城市转型的负向影响变为最大。

总体来看，尽管加入新的解释变量后原有各要素错配程度的解释力下降了，但是在考虑内生性后根据模型回归结果分析所得的研究结论依然保持了稳健性。

4.3 稳健性检验

4.3.1 剔除再生型城市样本

该研究的研究对象为资源型城市，而资源型城市的特点表现为以本地区矿产、森林等自然资源开采、加工产业为主导产业，在四类资源型城市中，再生型资源城市基本摆脱了资源依赖，城市的主导产业和经济结构已经发生改变，城市的经济决策和城市规划可能与同类城市迥异，城市的发展模式和发展方向与传统的资源型城市也已有明显不同，因此样本中包含再生型城市可能会影响该研究的回归结果。为了消除再生型城市样本带来的干扰，该研究根据《全国资源型城市可持续发展规划（2013—2020年）》所列再生型城市，将样本期内所有相关城市剔除，以进一步加强该研究回归结果的稳健性。具体剔除的城市包括：宿迁市、淄博市、唐山市、丽江市、葫芦岛市、马鞍山市、徐州市、南阳市、临沂市、鞍山市、洛阳市、盘锦市、张掖市、包头市、通化市，共计15个城市，剔除后样本城市剩余99个。以2005—2018年剩余99个资源型城市的面板数据重新进行双向固定效应的回归，回归结果报告于表6列（1）、列（2）。对比基准结果后发现，列（2）的资本要素错配程度在5%置信水平下通过检验，其余要素错配程度的回归系数均在1%的统计水平下显著为负，且按照回归系数绝对值大小排序，依次为劳动要素错配程度、资本要素错配程度以及能源要素错配程度，这与前文基准回归的结果一致，实证结果比较稳健，这说明要素错配会明显制约资源型城市的转型发展，并且各类资源型城市应当重视对劳动要素错配的缓解。

4.3.2 替换被解释变量

该研究在用DDF方法测算资源型城市的转型效率时，选取了实际地区生产总值作为期望产出。地区生产总值等于各产业增加值之和，是所有常驻单位在一定时期内生产活动的最终成果，以其作为期望产出能较全面地反映资源型城市的生产情况。但是资源型城市的产业发展有一定的特殊性，这些城市通常高度依赖资源的开采和加工，隶属于工业门类的资源型产业往往是城市的主导产业，因此资源型城市工业发展得好坏决定了城市的经济发展状况。在以往关于城市生产效率的研究中，也有学者选取工业总产值作为期望产出的指标。工业总产值是以货币形式表现的工业企业在一定时期内生产的已出售或可供出售工业产品总量，反映一定时间内工业生产的总规模和总水平。为了从不同角度反映要素错配对城市转型的影响，同时为了减少因指标选取而造成的偏误，该研究借鉴孙晓华的做法，选取工业总产值更替地区生产总值作为期望产出，重新测算资源型城市的转型效率。由于相关年鉴自2017年起不再统计工业总产值这一指标，因此各城市工业生产总值的数据时间跨度为2005至2016年。在缺乏各城市工业生产者出厂价格指数的情况下，利用省工业生产者出厂价格指数作为替代对各资源型城市的工业总产值进行平减。依旧在两种权重（1/9，1/9，1/9，1/3，1/3）和（0，0，1/3，1/3，1/3）设定下，重新计算分别得到转型效率trg和treg。

以2005—2016年114个资源型城市的面板数据重新进行双向固定效应的回归，表6的列（3）、列（4）汇报了采用trg和treg为被解释变量的回归结果。可以看出，列（3）、列（4）的能源要素错配程度分别在10%和5%置信水平下通过检验，其余各要素错配程度的回归系数仍在1%的水平下显著为负，验证了城市要素错配对城市转型的抑制效应，即增加城市要素错配程度会降低城市的转型效率，表明了该研究的主要结论是稳健的。比较表2基准回归的列（3）、列（6）和表6的列（3）、列（4）后还可以发现，替换被解释变量的回归系数绝对值要比原基准回归的小许多，这说明要素错配对城市的整体产出影响更大，而以资源型产业为代表的相关工业产业受到要素错配的影响更小，部分产业可能甚至会因要素错配成为相对受益者。

4.3.3 使用不同的回归方法

由于转型效率的取值范围为0到1，存在大量城市转型效率为1的样本，被解释变量拥有归并数据的特征，因此该研究使用Tobit模型进一步检验要素错配对城市转型的影响。另外，转型效率的高低仅由转型效率数值的大小反映，因而同比例扩大或缩小数倍数值并不会增添或减少信息，不会改变效率高低的排序，因此当统一对转型效率乘以100取整后，得到新的被解释变量tranfp和tranep，此时的转型效率数值有了计数变量的特点，计数多则意味着效率高，可以采用计数模型进行回归。tranf和trane的均值和标准差在乘以100后基本上与tranf和trane的均值和标准差一致，同时由于被解释变量的方差和期望显然不一致，因此该研究使用负二项回归模型来进行稳健性检验。以2005—2018年114个资源型城市的面板数据分别进行Tobit回归和负二项回归，两种回归模型的结果分别报告于表6的列（5）、列（6）和列（7）、列（8）。在采用了不同的模型进行回归后，要素错配程度的回归系数均在1%的水平下显著为负，要素错配仍然显著地抑制了城市转型，这与基准回归结果完全一致，进一步表明了该研究结果的稳健性。

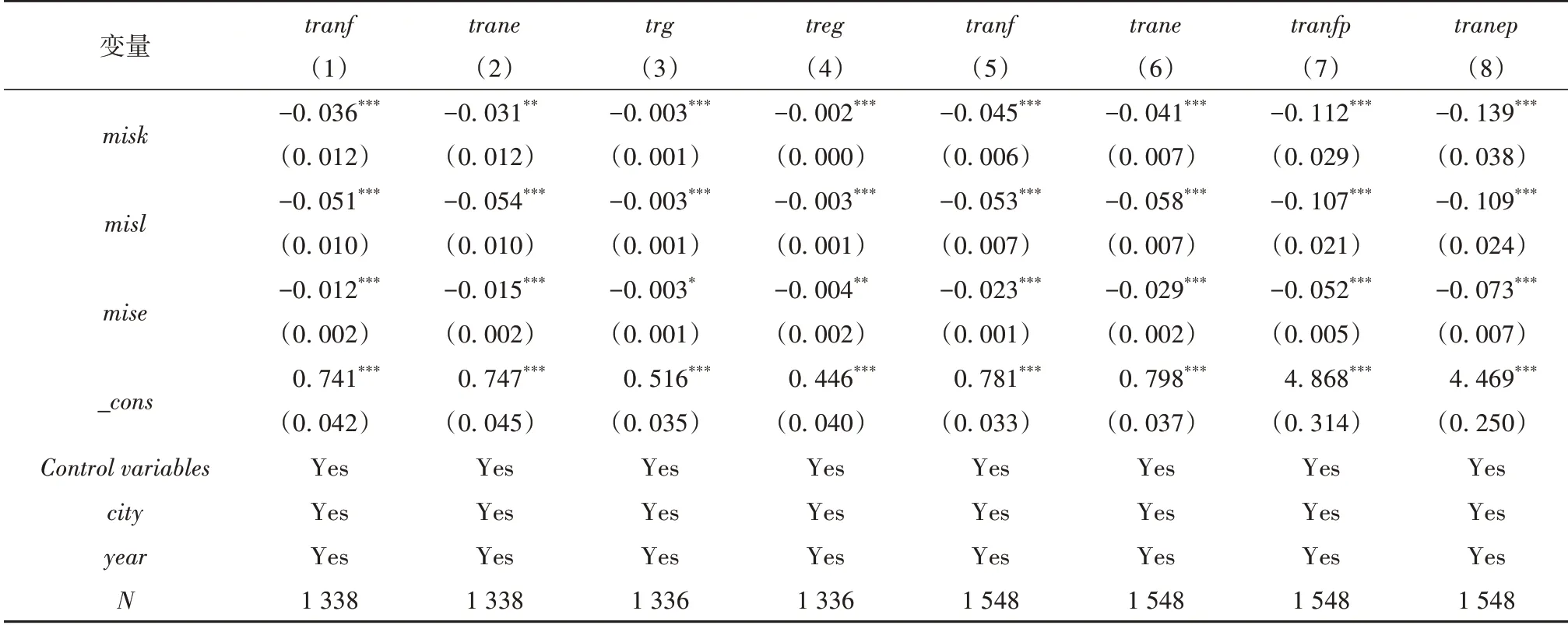
表6 稳健性检验回归结果

4.4 异质性检验

4.4.1 转型效率分解

根据前文的分析，资源型城市在只考虑能源投入的转型效率上与非资源型城市的效率水平相比，差距更为明显，更能体现资源型城市生产效率较低而非期望产出较多的特征，因此该研究分别对114个资源型城市的只考虑能源投入的转型效率进行分解，进一步得到各资源型城市2005—2018年在产出增长、能源消耗和环境友好三个方向上的生产效率，即产出效率（y），能源效率（e）和环境效率（env）。表7报告了要素错配与转型效率各分解部分的回归结果。可以看出，不论是否通过显著性检验，要素错配程度的回归系数均为负值，且仅有列（1）的资本要素错配程度回归系数未通过显著性检验，可知要素错配对资源型城市的产出效率、能源效率和环境效率均产生了显著的抑制作用。

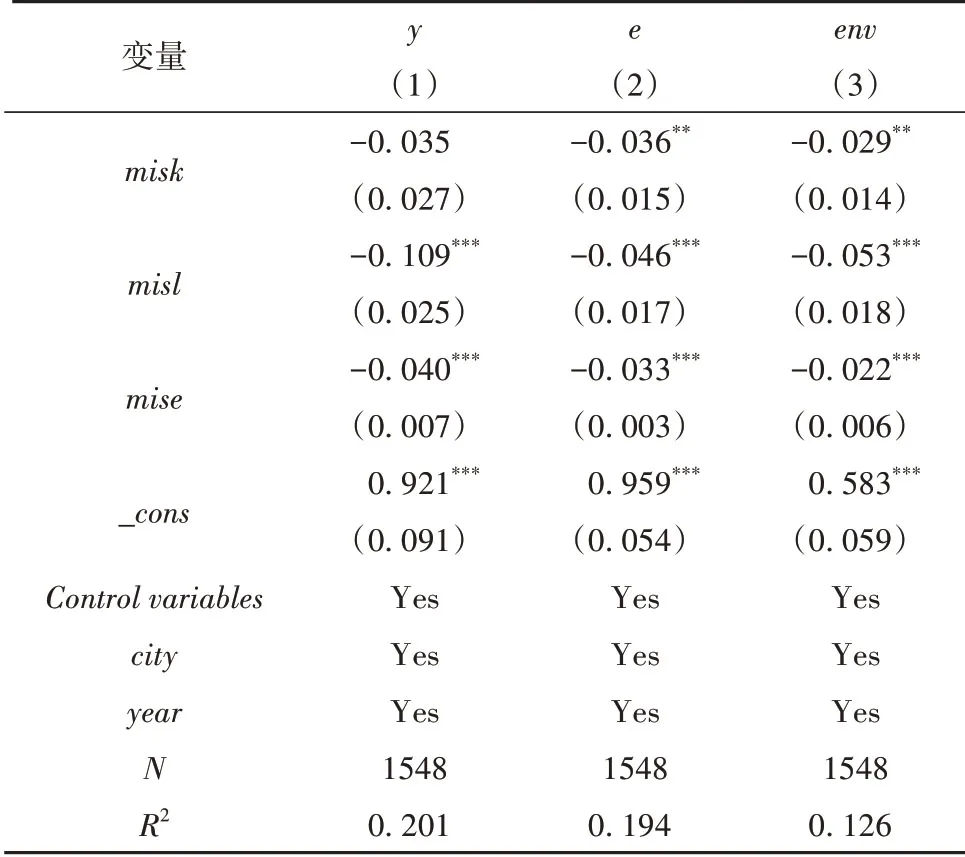
表7 转型效率分解的回归结果

对于产出效率而言，资本错配与其呈现负相关的关系但并不显著，而劳动错配和能源错配则在1%的置信水平下通过检验，表明劳动错配和能源错配会显著抑制城市产出效率的提升，并且劳动错配的抑制作用尤为明显，这可能是因为：能源错配对产出的影响更局限于资源型产业，其他行业对能源的依赖较小，仅需保证正常使用便可正常运转，更多占有能源也不会明显增大产出；与此能源要素相反，劳动要素的错配则会影响整个社会的产出，一方面资源型产业无法吸引高素质劳动者以进行人力资本积累，相关行业的生产效率无法有效提高，劳动要素的边际产量较少；另一方面相关人才会流入到其他行业，尤其金融业、公共服务业，造成劳动配置过度，最终使整个社会的产出效率下降。对于能源效率和环境效率而言，各要素错配程度的回归系数均显著为负，表明要素错配会阻碍城市能源效率和环境效率的提升。在所有要素中，劳动要素错配程度回归系数的绝对值依然是最大的，这表明劳动要素错配对城市转型的影响最大，这与基准回归的结果一致，进一步强调缓解劳动要素错配对城市转型发展的重要性。

4.4.2 不同地理区域

中国区域间经济发展不平衡的现象十分突出，东部、中部、西部三大区域间的经济社会发展水平差异极大，因而不同地区的资源型城市有着各自的发展历史和特点，将114个资源型城市按照所在省份分为东部、中部、西部和东北部，来检验要素错配对城市转型效率的差异化影响。表8和表9分别报告了分区域情况下两种转型效率的回归结果。

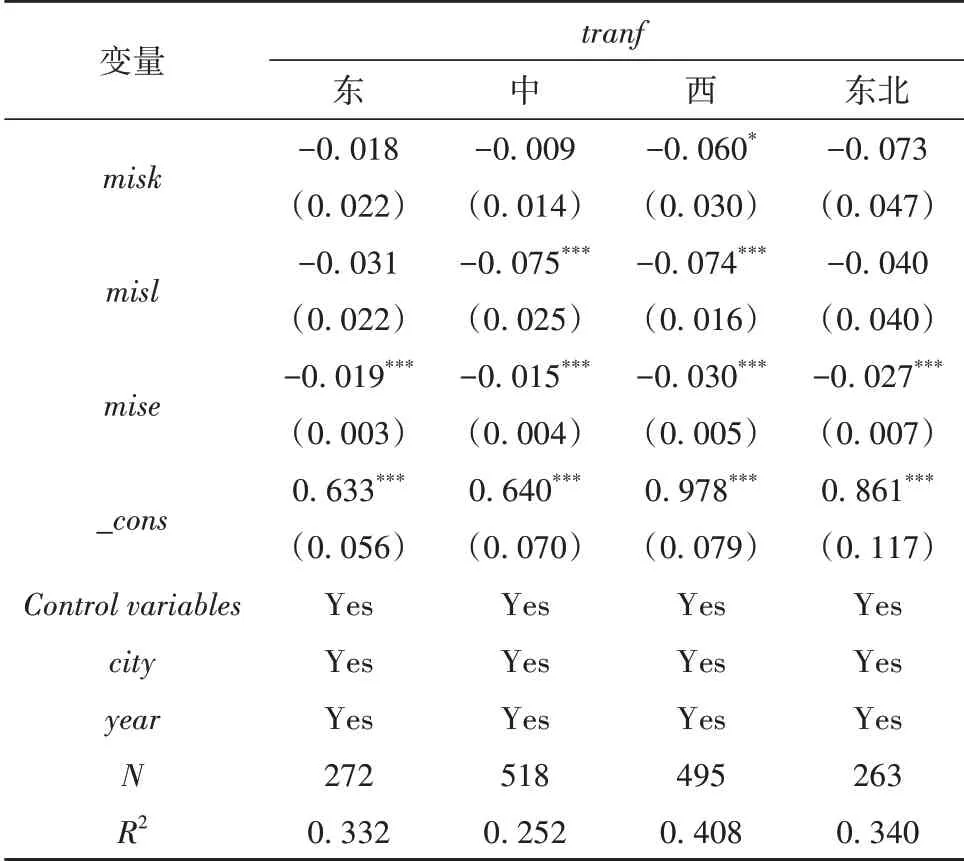
表8 分区域回归结果一

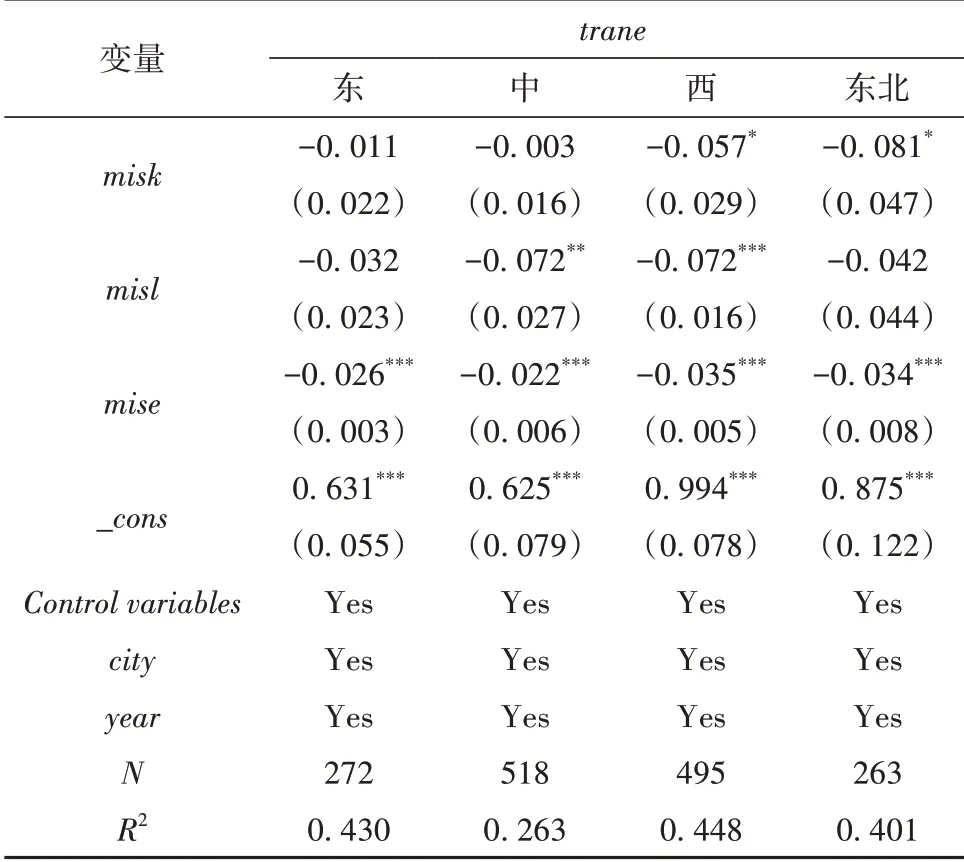
表9 分区域回归结果二

可以看出，无论在东中部、东北，还是西部城市，要素错配程度对城市转型效率的影响系数均为负值。其中，东部城市只有能源错配显著地抑制了转型效率的提升；中部城市的劳动错配和能源错配会同时制约着城市的转型；西部城市各要素错配均会对城市的转型产生显著的负影响；对于同时考虑资本、劳动和能源的转型效率而言，东北城市只有能源要素的错配会对城市的转型效率产生抑制作用，对于只考虑能源投入的转型效率而言，资本要素错配也会有明显的抑制效应。特别需要注意的是，西部地区和东北地区，尤其是东北地区，资本要素错配对城市转型效率的抑制作用要明显高于其他地区，而劳动要素错配程度的影响系数反倒并不显著。可能的原因在于：一方面由于划分后东北地区城市数量是最少的，过少的样本量导致估计系数不显著；另一方面，东北的资源型城市开发较早，东北作为老工业基地城市化、工业化水平较高，工业化发展处在相对较高阶段，并不单纯依靠采掘资源等低端产业实现城市发展，而且由于城市存在大量的国有企业，导致劳动要素的内部流动并不如东部地区频繁，不会导致各行业产出变动过大，因此劳动要素错配程度的影响系数反倒减小。

5 结论与政策建议

面临日益强化的资源环境约束，资源型城市的转型升级问题已经成为关注和讨论的热点问题。在有序推进碳达峰、碳中和以及深化供给侧结构性改革的背景下，该研究从要素错配的全新视角，探讨了资源型城市陷入经济转型困境的内在原因。在此基础上，该研究重点研究了三个主要问题。一是科学识别了资源型城市经济转型效率；二是梳理了要素错配在经济增长、能源消耗以及环境保护等方面影响资源型城市转型的作用机理；三是实证检验了要素错配对资源型城市经济转型的影响。得到以下主要结论。

（1）基于Cobb-Douglas生产函数构建了旨在分析要素错配对经济转型效率的理论分析框架，提出要素错配影响经济转型的内在机制：行业间的要素错配通过抑制产业结构的转型升级降低资源型城市的产出效率和环境效率；用途间的能源错配通过鼓励企业使用能源对技术进行替代降低了能源效率和环境效率。而能源等要素在产业间的错配会挤占替代产业发展所需要素，抑制城市产业结构升级，引发能源效率和环境效率的损失，阻碍资源型城市产业转型。

（2）基于中国114个资源型城市2005—2018年的面板数据来研究要素错配对资源型城市转型升级的影响。采用固定效应模型得到基准回归，发现资源型城市要素错配程度与转型效率呈现出显著的负相关关系，无论是要素配置过度还是配置不足，要素错配对于资源型城市的经济转型均存在明显的抑制作用，且劳动错配抑制作用尤为明显。在缓解内生性问题和进行稳健性检验后，主要实证结果仍未发生变化。来自东、中、西和东北地区的异质性检验显示，要素错配对资源型城市转型效率的影响因所处区域不同存在差异。

根据上述研究结论，可以得到三个方面的政策建议：①国家层面，应统筹推进自然资源资产的产权制度改革，增强市场纠错主体地位，明晰在占有、使用、处置资源的过程中的权力界定，避免发生权力寻租，发挥市场在资源配置中的决定性作用；同时，要建立健全补偿机制，发挥政府兜底作用，完善资源开发前的环境服务支付费制度，打造资源开发过程的边开发边修复模式，形成开发完成后资源型地区的生态恢复制度。②在城市层面，要引导要素流动以建设多元化的产业体系，依靠接替产业和新兴产业为城市发展赋能，激发资源型城市发展内生动力；加强高素质劳动要素的培养、引进，双措并举，提高劳动要素的配置效率。③产业层面，地方政府应利用绿色财政，使用转型扶持资金支持资源型企业引进开发新工艺，打通堵点补充断点，实现技术补链，辅助龙头企业突破关键技术和环节的缺失和瓶颈，实现资源的深加工，提升产品附加值；而且，要扶持龙头企业建立产业集群，并购重组整合资源，发挥规模效应，打通产业链上下游，完成纵向产业链对接，实现对传统资源型产业的改造提升。

该研究的不足之处在于，限于数据获取来源，选取工业用电量作为能源消耗的衡量指标，利用工业废水、工业二氧化硫和工业烟尘三种污染排放物衡量污染排放，得到的综合污染排放指数不包括固体废弃物污染等，可能无法全面地表征非期望产出。同时，选择各城市职工平均在岗人数衡量劳动投入，没有充分考虑劳动者素质之间的差异，而随着数字经济时代的到来，高素质劳动力蕴含的人力资本对于资源型城市转型发展的作用可能更为明显。在未来研究中，随着各界对数据要素资本的重视和数据获取渠道的逐步完善，上述问题有望得到有效解决。