基于深度神经网络的航天器反交会逃逸方法
陆鹏飞,王 悦*,石 恒,汤 亮
1.北京航空航天大学宇航学院,北京 102206
2.北京控制工程研究所,北京 100094
3.空间智能控制技术重点实验室,北京 100094
0 引 言
随着人类航天科学与技术的发展,近地轨道上的航天器数量越来越多,这给在轨航天器的正常运行带来了诸多潜在威胁.一方面,轨道上大量的空间碎片容易与正常运行的航天器发生碰撞,造成航天器的损坏;而另一方面,有些航天器具有主动变轨能力,可以接近其它航天器并进行非合作交会等操作.因此,有必要针对在轨航天器的反交会逃逸技术进行研究,以提高航天器的生存能力.
很多学者对追逃博弈进行了研究,文献[1-3]分别采用直接法、间接法、半直接法等数值方法求解得到双方均为最优的追逃策略.其中直接法将微分对策问题中的状态量或控制量离散化,将原问题转化为数学规划问题求解,有直接打靶法(也称为直接控制量参数化方法)和直接配点法等方法;间接法指利用微分对策问题的必要条件,将原问题转化为边值问题来求解;在半直接法中,追逃博弈双方中一方的最优策略采用必要条件求解,而另一方的最优策略使用直接法求解.文献[4]基于状态依赖Riccati方程推导出Hill坐标系下追逃问题的非线性控制律,文献[5]通过无迹卡尔曼滤波估计参数,对信息获取不完全时的追逃进行策略求解.追逃博弈数学理论严密,但也有一定的局限性:当追踪方不采用鞍点解时,对于逃逸方鞍点解也不再是最优;此外,这些研究里都用到复杂的数值方法,求解速度慢,无法在轨快速得出结果.反交会规避技术从空间碎片碰撞规避相关的研究发展而来[6-7],在对追踪航天器的状态测量与接近策略的合理假设下,优化逃逸机动脉冲,使得既定的指标最优[8-9].文献[8]定义潜在威胁区为指标,采用遗传算法优化逃逸脉冲,以减小被交会的可能.此类方法的核心是求解优化问题,目前普遍使用启发式算法等全局优化算法以避免陷入局部极值,计算量大,难以在轨实时快速实现,可能造成面对非合作交会威胁时,航天器无法及时逃逸的后果.
为提高航天器智能化能力[10],近些年不少研究将机器学习应用于制导控制律求解[11].文献[12-13]将深度神经网络用于着陆过程最优制导律的求解,而文献[14]和[15]分别使用强化学习和深度强化学习解决软着陆中的制导问题.另一些研究中深度学习技术被用于优化小推力转移轨道[16-18].这类研究通过对神经网络进行训练,可以建立系统状态与最优控制量之间的对应关系,从而根据当前状态量快速生成近似的最优控制量.该方面的研究为航天器反交会逃逸的智能化与实时化提供了新思路.
本文针对目前逃逸机动计算复杂,无法在轨快速实时生成的问题,提出使用深度神经网络线下学习最优逃逸脉冲的生成规律,以实现航天器在轨快速实时生成最优的逃逸脉冲.首先,构造了描述逃逸脉冲的双层数学规划问题模型;然后确定神经网络的输入与输出,使用粒子群优化算法计算两航天器不同相对状态下的逃逸脉冲,构建数据集;最后,设计并训练神经网络,并研究了网络超参数对学习效果的影响和网络的泛化能力,通过仿真验证了所提出方法的有效性.
1 场景描述与相对运动动力学建模
1.1 近距离反交会逃逸问题概述
考虑以下场景:两航天器在地球附近轨道上近距离飞行,其中一个航天器(追踪航天器)试图接近并交会另外一个航天器(逃逸航天器),逃逸航天器察觉到追踪航天器的接近意图,采取轨道逃逸机动躲避追踪航天器的交会,使得自己不被交会的可能性提高.为了与工程中常用的轨道控制方式相符合,设追逃双方航天器的轨道机动方式都为脉冲机动.
我们的研究中,只考虑逃逸航天器的逃逸机动策略求解,对于追踪航天器追踪策略的设计不在本文考虑范围内.但是,逃逸航天器的逃逸策略设计往往需要根据追踪航天器的状态与实际接近策略进行考虑,故需要对追踪航天器的接近策略进行合理假设.因此,本文中涉及的追踪航天器接近与交会策略,都是站在逃逸航天器角度的“假想”,以服务于逃逸策略的设计.实际中为了节省燃料以完成后续任务,追踪航天器往往会规划自身的交会策略,在一定时间内以最小的脉冲消耗代价完成交会.所以我们合理地假设追踪方是“理性人”,其可以规划交会导引的方式,优化变轨脉冲消耗完成非合作交会,以节省燃料进行后续在轨操作.因此,本文后续的研究中,追踪航天器的交会导引方式以最小燃料消耗的多脉冲接近方式进行.在该假设中,一个重要的参数是交会时间上限的选取,该值会较大地影响交会燃料消耗,在实际中需要根据多方面的信息,如两个航天器的相对位置与相对速度、追踪航天器的发动机推力信息、对方的战术意图等合理设置.
实际中当地面测控系统或天基预警系统检测到追踪航天器近距离靠近逃逸航天器时,测控系统将双方的相对状态信息提供给逃逸航天器,逃逸航天器星载计算机需立刻计算出逃逸脉冲.本文提供了根据两航天器的相对状态,快速计算出近似最优逃逸脉冲的方法.最优的评判原则为:考虑到航天器携带的燃料是有限的,燃料的上限决定了其最终的可机动能力,而追逃双方的空间对抗往往会持续一段时间,逃逸航天器若用有限的消耗保持自身安全的同时让对方燃料消耗最大,会让自己在对抗中占据优势.故本文中采取的指标是追踪航天器交会逃逸航天器的燃料消耗,即逃逸航天器最优的逃逸脉冲应当使得追踪航天器完成交会任务的燃料消耗最多,也即是让追踪航天器非合作交会的代价最大.
传统的追逃博弈理论中最终得到的是开环的、依赖于时间的逃逸策略,本文的方法相比其更有优势.在本文中,逃逸脉冲的计算只依赖于计算时刻测得的两航天器的相对状态,而不依赖于时间.逃逸航天器可以根据监测到的相对状态间隔一定时间多次进行逃逸变轨,形成闭环,以规避追踪航天器的持续接近.本文中我们只对逃逸航天器单次逃逸脉冲的生成方法进行研究,当航天器需要多次逃逸时,每次脉冲的计算方法都是相同的,只需改变届时的状态参数.
1.2 相对运动动力学建模
设地球引力场为完全中心引力场,逃逸航天器以近圆轨道飞行,追踪航天器在其附近.追踪航天器用质点P表示,逃逸航天器用质点E表示,如图1所示.设想在P与E附近有一虚拟动点O以圆轨道运动,称其轨道角速率ω为参考轨道角速率.建立以O为原点的轨道坐标系OXYZ,称为参考轨道坐标系,其中Z轴指向地心,X轴在轨道平面内垂直于Z轴,指向与参考点运动方向一致,Y轴由右手定则确定.则P与E相对O点的运动可用坐标系OXYZ下的CW方程描述为
(1)
式中:i=P,E分别代表追踪航天器与逃逸航天器;xi,yi,zi为P或E相对O的位置矢量在OXYZ中的3个分量;fix,fiy,fiz表示施加在航天器上的控制加速度在OXYZ中的分量.用追踪航天器相对O点的运动方程减去逃逸航天器相对O点的运动方程,可得追踪航天器相对逃逸航天器的运动方程
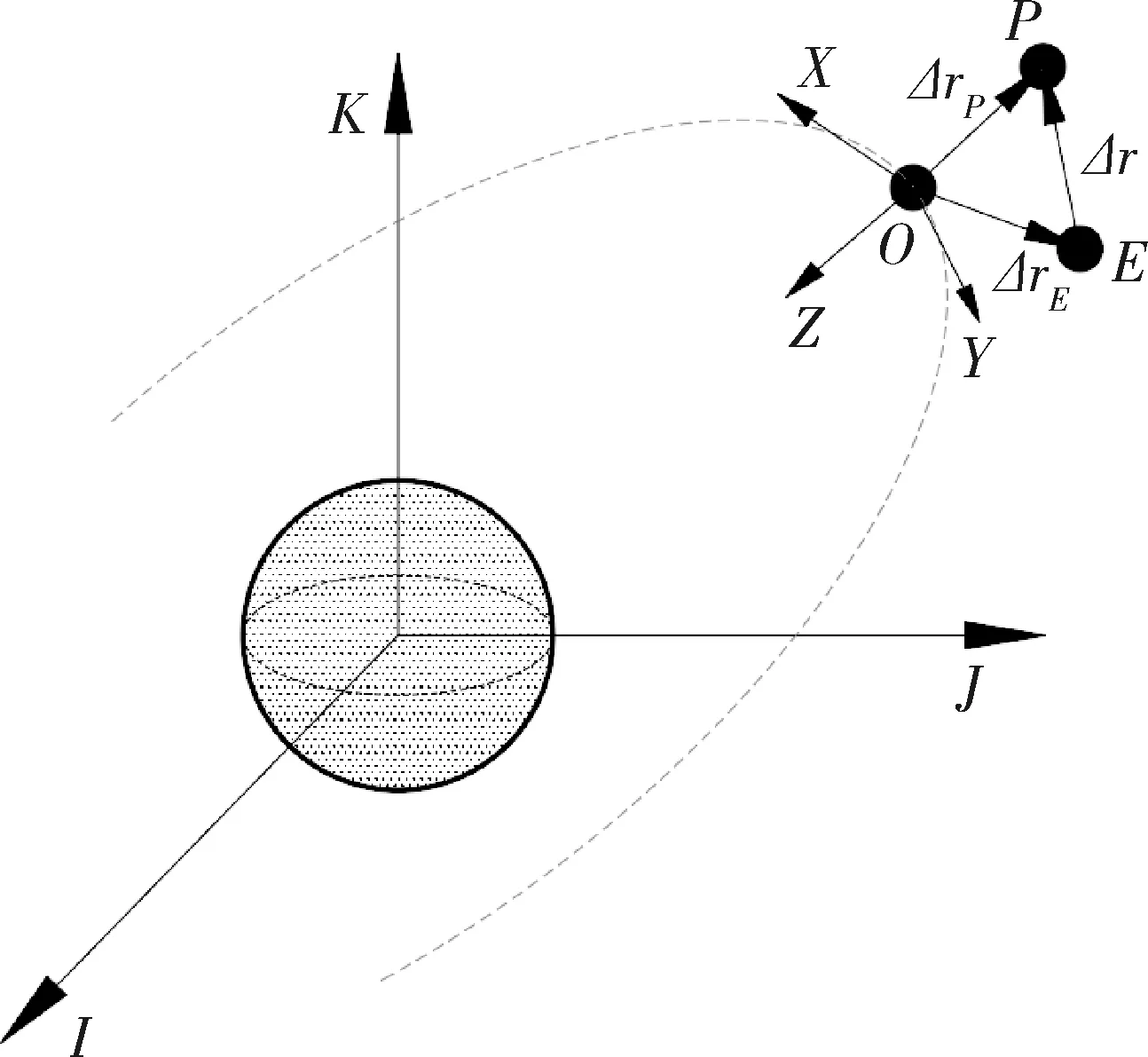
图1 近距离相对运动示意图Fig.1 Schematic diagram of close-proximity relative motion
(2)
式中,x,y,z表示追踪航天器相对逃逸航天器位置矢量Δr在OXYZ中的3个分量.


(3)
式中,A和B为常系数矩阵,其表达可参考文献[19].
进一步,常系数常微分方程组(3)的解可表示为
(4)
式中,t0为初始时刻,X0为状态变量在初始时刻的值,Φ(t,t0)为状态转移矩阵,其表达式为
(5)
式中,υ=ω(t-t0).
在双方航天器轨道控制都以脉冲方式进行时,式(4)变为

(6)
式中:ti,tj分别是追踪航天器和逃逸航天器脉冲机动的时刻;M,N是两航天器在时刻t之前脉冲机动的总次数;ΔvPi,ΔvEj分别是两航天器在ti,tj时刻的脉冲机动速度增量矢量.该式描述了两航天器相对状态与各自速度脉冲的关系.
2 最优逃逸脉冲求解的双层数学规划模型
2.1 逃逸脉冲设计思路
当感知到追踪航天器的接近威胁时,无论追踪航天器实际是否去实施非合作交会操作,逃逸航天器都“假想”追踪航天器将会以最小消耗多脉冲变轨的方式,在某个时间上限T内对自己进行交会,并据此制定逃逸策略,即求解出逃逸脉冲的大小与方向.
逃逸航天器制定逃逸策略的依据是:自己变轨逃逸后,追踪航天器即使能够完全测得自己变轨后的状态,并且作为“理性人”去以此优化多脉冲交会的轨迹的情况下,仍然需要消耗最多的燃料(最大的机动脉冲代价)来完成交会.
由于逃逸策略的制定建立在“假想”追踪航天器将会规划变轨机动并对自己进行交会的基础上,所以逃逸脉冲优化中需要调用最小消耗多脉冲交会优化模型,形成一种双层结构,我们称之为双层数学规划模型.逃逸脉冲的计算通过求解双层数学规划模型实现.按照上述思路,首先我们需构建追踪航天器近距离最小消耗多脉冲交会的优化模型,其次构建逃逸航天器逃逸脉冲的优化模型.
2.2 近距离最小消耗多脉冲交会问题
最小消耗多脉冲交会的优化,是逃逸航天器“假想”自身按某种方式变轨后,追踪航天器完成非合作交会的方式优化,具体需要优化的量为追踪航天器变轨脉冲各次的时刻与对应的脉冲方向及大小,使得在给定时间上限T内与逃逸航天器交会,并且消耗的总速度增量最小.两航天器相对状态可由式(6)忽略逃逸航天器的脉冲后得到:
(7)
设初始时刻为t0,初始时刻追踪航天器在参考轨道坐标系下的状态X0,追踪航天器共采取N次速度脉冲,脉冲时刻分别为t1,t2,…tN,最后一次脉冲实现与逃逸航天器的交会.
以脉冲时刻和前N-2次速度增量矢量为优化变量,表示为[t1,…,tN,Δv1,…,ΔvN-2]T,共计4N-6个优化变量.以N次脉冲速度增量之和为优化目标,表达式为
(8)
考虑追踪航天器第N-1次脉冲后至第N次脉冲前的这一段自然飞行,其状态转移可表述为
X(tN)=Φ(tN,tN-1)X(tN-1)
(9)
写为分块矩阵相乘的形式
(10)
符号“-”与“+”分别表示脉冲前与脉冲后.

(11)

(12)
这样只需将前N-2次脉冲以及所有的脉冲时刻作为优化变量,便可以将目标函数中最后两次脉冲大小用优化变量表出,从而构造出不含非线性等式约束的最小消耗多脉冲交会问题优化模型,表述如下:
s.t.
根据表1中的数据,并按照公式(1)对lgtind与lgs进行线性拟合计算,可得到两者的关系式,结果如图8所示。
(13)
其中,|Δvi|为第i次脉冲的模值,αi和βi是第i次脉冲的方位角和高低角,定义与图2中一致;目标函数中第N-1次和第N次脉冲大小按下述式(14)~式(18)给出.

(14)
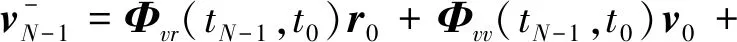
(15)
(16)

(17)
(18)
由于式(14)~式(18)中状态转移矩阵Φ的各分块中都含有非线性项(三角函数),故该目标函数是复杂的非线性函数,优化问题无法用解析方法获得其最优解,需通过数值方法求解.
2.3 逃逸脉冲优化
逃逸航天器以脉冲ΔvE进行逃逸机动,我们将其速度脉冲大小|ΔvE|,速度脉冲方位角αE和高低角βE(在参考轨道坐标系下定义,示意图如图2)作为优化变量.由于本文中只考虑单次变轨逃逸,并旨在建立逃逸脉冲与两航天器相对状态之间的对应关系,解出的逃逸策略不依赖于时间,故逃逸脉冲执行时刻不参与优化.
当逃逸航天器执行大小为|ΔvE|,方向角为αE、βE的逃逸脉冲后,两航天器之间的相对状态会发生改变,则可用2.2中的模型(13)求解出对应该逃逸脉冲被执行后追踪航天器最小交会消耗JE.因此,这个过程建立了|ΔvE|、αE、βE三个描述逃逸脉冲的变量与JE的映射关系,将映射关系记为f(·),有
JE=f(|ΔvE|,αE,βE)
(19)
以该函数的最大化为目标,我们构建出求解逃逸航天器最优逃逸脉冲的优化模型
maxJE=f(|ΔvE|,αE,βE)
s.t.
(20)
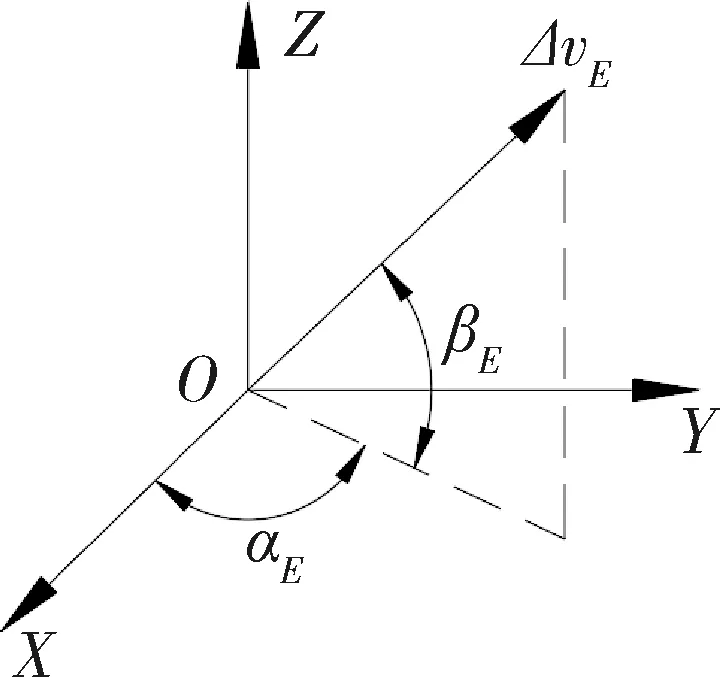
图2 脉冲方位角和高低角的定义Fig.2 Definition of azimuth and elevation of impulses
根据前文所述的设计思路,逃逸脉冲优化中需要调用最小消耗多脉冲交会优化模型,形成一种双层数学规划模型.如图3所示,问题求解的整体结构为:逃逸脉冲优化(上层优化)过程针对可行域中的逃逸脉冲大小与方向,生成对应的未来相对状态,再分别调用多脉冲交会优化(底层优化)问题,以求解在未来各相对状态下假想的对方交会最小脉冲消耗值,并将其作为当前可行解对应的目标函数值反馈,最终将交会最小消耗的最大值对应的解作为最优解.该问题的求解较为复杂,需要先使用优化算法求解底层优化问题,建立上层优化变量与底层最优值之间的对应,然后再次使用优化算法求解上层优化问题,得到最优逃逸脉冲.
需要注意的是,无论是底层优化问题还是上层优化问题都有很多局部解,且上层优化问题并没有解析的目标函数,若用传统的优化方法,如序列二次规划(SQP)等求解很容易陷入局部极值点,所以要选择能够跳出局部解的启发式算法,如遗传算法(GA)、粒子群算法(PSO)等[20].而这些算法虽然能够寻找全局解,但是计算量非常大,尤其是在解决本文中的双层数学规划问题时,需要很长的求解时间,无法在星载计算机上快速得到结果,导致在对抗中不能实时生成当前形势下的最优逃逸脉冲.所以,本文接下来提出使用深度神经网络学习最优逃逸脉冲的计算规律,以实现逃逸脉冲的在轨实时快速生成.

图3 双层数学规划模型结构Fig.3 Structure of double-layer mathematical programming model
3 基于深度神经网络的逃逸脉冲求解
3.1 样本集的构建

式(7)中状态转移矩阵只依赖参考轨道角速率ω,再根据(13)、(20)可知,在参考轨道角速率ω、假定的追踪航天器交会时间上限T以及两航天器当前相对状态X给定后,便可以通过求解双层数学规划问题唯一确定出最优的逃逸脉冲方向.对于特定的航天器,其轨道高度是一定的,故参考圆轨道角速率ω可作为背景参数给出.交会时间上限T与实际对抗场景中追踪航天器参数有关,我们也将其作为背景参数.这样由两航天器当前相对状态X便可唯一地确定逃逸航天器最优的逃逸脉冲方向,即
(21)
故我们将训练样本的特征选定为当前相对状态X的6个分量,也即网络的输入.
综上,确定神经网络的输入为一个6维向量[xyzvxvyvz]T,输出为一个2维向量[αEβE]T.
确定神经网络的输入与输出后,便可以构建样本集用于训练、验证与测试.样本集中的每一条样本由样本特征与样本标签值构成,样本特征对应网络的输入,样本标签值对应网络的输出.选择大量的初始相对状态,计算它们对应的最优逃逸脉冲方向,可以得到一系列样本,构成样本集.
3.2 深度神经网络的架构
在特定的问题中,神经网络的类型、神经元的种类(激活函数的种类)和网络的隐藏层数以及每层神经元个数在很大程度上决定了其学习能力,需要合理地选择.
根据式(21),网络的输出仅依赖于当前的两航天器相对状态,与历史状态无关,这表示前馈神经网络类型较适合于该问题.在前馈神经网络中,第一层为输入层,最后一层为输出层,中间层为隐藏层.每一层的神经元接受前一层神经元的信号,并产生信号输出到下一层.信息在网络中传播的迭代公式为
(22)
式中:z(l)表示第l层神经元的净输入,a(l)表示第l层神经元的输出;W(l)∈RMl×Ml-1是第l-1层到第l层的权重矩阵,其中Ml表示第l层神经元个数;b(l)∈RMl是第l-1层到第l层的偏置量;fl(·)表示激活函数.
激活函数是一个非线性函数,决定神经元的类型.常用的激活函数有Logistic函数、双曲正切(Tanh)函数、修正线性单元(ReLU)函数等.对于隐藏层神经元激活函数的选择,考虑到ReLU函数可以有效解决深度网络训练时的梯度消失问题,提升网络的学习能力与训练效果,所以我们选择其作为隐藏层神经元的激活函数.为说明优势,在后文仿真结果中也给出ReLU函数与Logistic函数分别用于隐藏层神经元的效果对比;对于输出层,我们把所有训练数据归一化到[-1,1]之间,所以选择值域为(-1,1)的Tanh函数作为激活函数.为了比较效果,我们也用线性(Linear)层作为输出层,在数值实例中与Tanh函数作对比.设计不同的隐藏层与输出层神经元种类的组合如表1所示.

表1 不同的隐藏层与输出层神经元组合Tab.1 Combinations of different types of neurons for hidden and output layers
对于神经网络的隐藏层数和每层神经元的个数选择,文献[12,16]中证明多个隐藏层的深度神经网络才能够很好地学习到最优控制律.这里我们设计的网络中,既包含只有一层隐藏层的浅网络,也包含具备多个隐藏层的深度网络,网络隐藏层数与每层神经元的个数如表2所示,在后文数值实例中比较它们的学习效果.
4 数值实例
4.1 PSO算法求解最优逃逸脉冲
相关参数设定为:参考点圆轨道高度为300 km,初始时刻t0=0,初始时刻逃逸航天器与追踪航天器的轨道6要素如表3所示.可以求得在参考轨道坐标系中追踪航天器相对逃逸航天器的位置为r0=[-13.15,0.32,-12.18]Tkm,相对速度为v0=[-23.02,-5.44,1.18]Tm/s.假设的追踪航天器接近策略为三脉冲最小消耗交会,交会时间上限T=1800 s.这里选择脉冲数为3是参考了文献[21].使用PSO算法对问题(20)进行求解,其中求解底层优化时,粒子个数取20,迭代次数为1000;求解上层优化时,粒子个数取10,迭代次数为100.取不同的逃逸脉冲允许上限值Δvmax,所得到的最优的逃逸脉冲方位角、高低角以及最优脉冲大小结果见表4,表中结果验证了上文中所说的逃逸脉冲方向是反映逃逸脉冲优劣的属性.


表2 不同隐藏层数与单层神经元个数的组合Tab.2 Combinations of different numbers of hidden layers and units per layer

表3 初始轨道要素取值Tab.3 Values of initial orbit elements

图4 追踪航天器交会最小消耗与逃逸脉冲方向的关系Fig.4 The minimum fuel consumption for pursuer in relation to the direction of impulsive evasion

表4 逃逸脉冲优化结果Tab.4 Optimal solutions of evasive impulses
4.2 神经网络训练与结果分析
设参考点圆轨道高度为300 km,假定的追踪航天器交会时间上限T=1800 s.取不同的两航天器相对状态求解最优逃逸脉冲以构建样本集,其中相对距离在10~50 km内间隔10 km选取,相对速度大小在11~35 m/s内间隔3 m/s选取,相对位置和相对速度的方位角与高低角分别在0~2π和-π/2~π/2等间隔选取.共计得到1393920对相对状态与最优逃逸脉冲,我们将80%的数据(1115136对)用于训练,10%的数据(139392对)用于训练过程中的验证,10%的数据用于训练完成后泛化性能的测试.为了消除因数据尺度不同而造成的训练难度,将所有的数据都进行归一化处理,归一化的原则见式(23),归一化后的数据在[-1,1]之间.
(23)

对表1中的4种隐藏层与输出层神经元种类的组合,我们训练4个前馈神经网络分别对应,这些网络都具备8层隐藏层,每个隐藏层包含64个神经元.利用均方误差(MSE)作为损失函数,训练过程使用Adam算法对网络权重进行优化,Adam算法中学习率取为lr=0.005,梯度一阶矩估计和二阶矩估计的指数衰减率设为β1=0.9,β2=0.999,训练集分为小批量参与训练,每批包含1000个样本,对整个样本集的最大训练轮数为50,取在验证集上表现最好的权重为训练完成后的最终权重.训练结束后的神经网络在验证集上和测试集上的均方误差如表5所示.将神经网络输出的脉冲方向和优化算法计算出的脉冲方向在三维空间中的夹角(角度制)定为神经网络的输出误差,图5给出了这些网络在测试集上的输出误差小于特定值的样本所占比例(准确率)随误差变化的曲线.从结果中可以看出,用ReLU函数作为隐藏层神经元的激活函数,Tanh函数作为输出层神经元的激活函数,所训练出的网络,训练时的误差和测试时的泛化误差均最小,输出的脉冲方向准确率最高,测试集中的样本有接近90%的比例都输出误差在5°以下.而Logistic函数作为隐藏层神经元激活函数,效果远不如ReLU函数,证明了前文所说的ReLU函数的优势.
对表2中的5组隐藏层数与每层神经元个数的组合,我们训练出5个神经网络分别对应,每个网络隐藏层神经元激活函数都使用ReLU函数,输出层神经元激活函数使用Tanh函数,训练过程的其他参数与上文中相同,训练完成后的这些网络在验证集和测试集上的均方误差见表6,图6给出了测试集上样本输出误差小于特定值所占的比例随输出误差的变化.对比序号1、2、3的结果可以发现,在神经元总数目相同时,网络深度的增加可以极大地提高学习能力,单层网络即使神经元数很多也不能够很好地掌握所要学习的规律,这与文献[12,16]中的结论保持一致;对比序号3、4、5可以发现,一定程度上,随着网络的隐藏层数和每层神经元个数增多,其输出的均方误差更小,准确率更高,学习最优逃逸脉冲生成规律的效果更好.但是这种增益效果随着网络大小的增加而衰减.
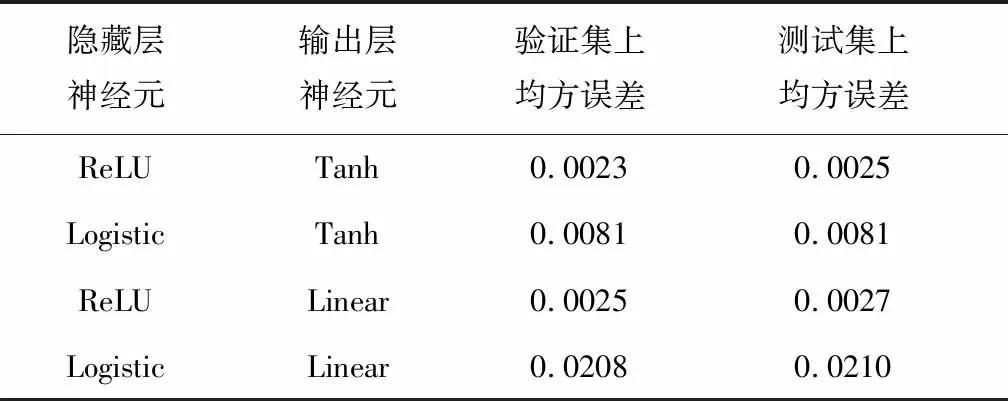
表5 不同神经元类型的深度神经网络均方误差Tab.5 MSE of DNNs with different types of neurons
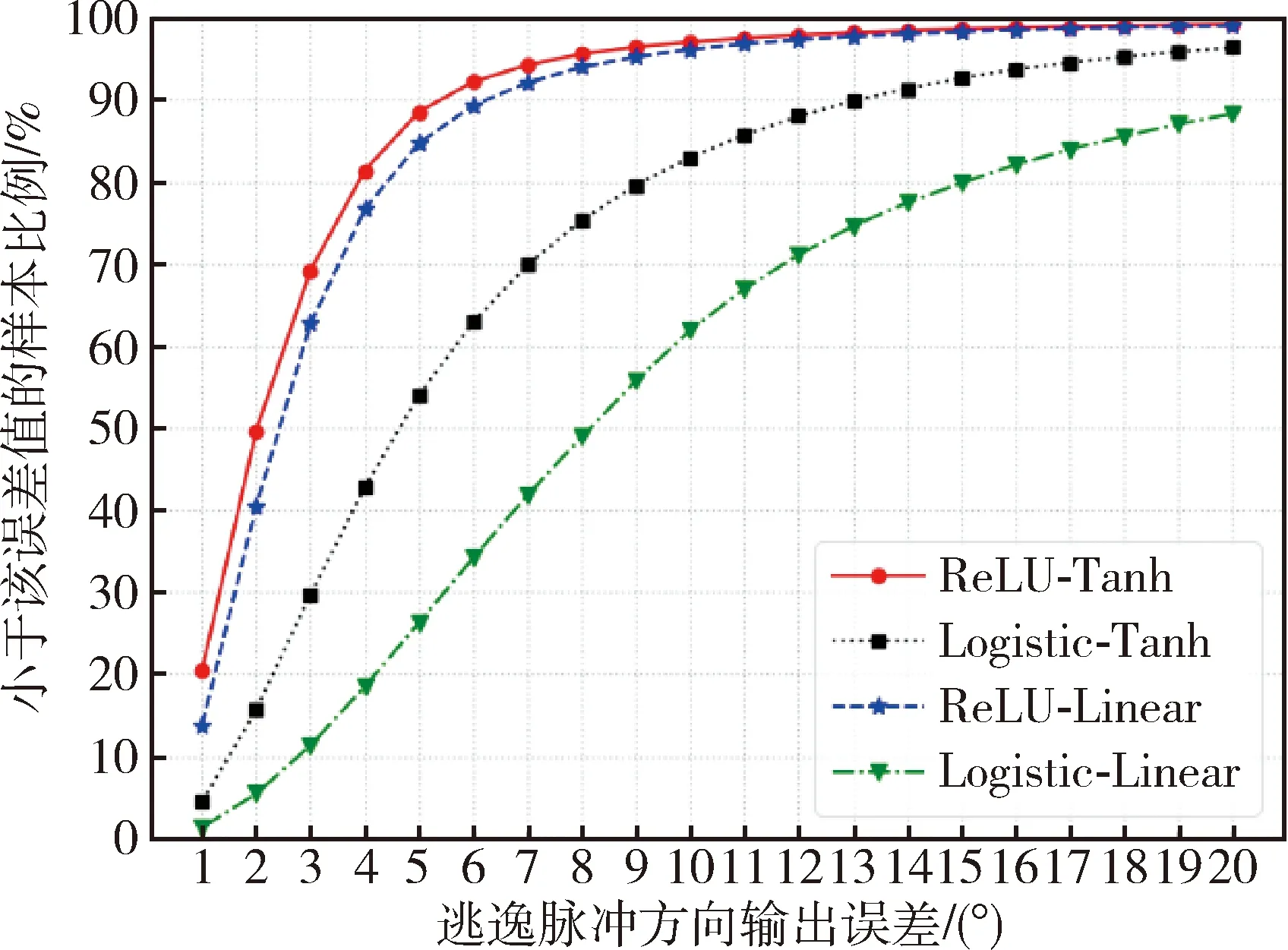
图5 不同神经元类型的深度神经网络输出脉冲方向准确率Fig.5 The accuracy of outputs of DNNs with different neurons

表6 不同规模的神经网络均方误差Tab.6 MSE of ANNs with different sizes

图6 不同规模的神经网络输出脉冲方向准确率Fig.6 The accuracy of outputs of NNs with different size
4.3 深度神经网络方法准确度分析
以4.1中的参数为例,让逃逸航天器的实际逃逸方向与优化算法求出的最优方向产生不大的偏差,则对应的追踪方完成交会过程的最优消耗与原最大值也会产生一定偏差,偏差的具体情况在图7中给出,图中极角0°~360°表示与优化算法求出的最优方向成固定偏差角的方向集合(空间中一个圆锥面),极径表示导致追踪方最优消耗偏差的大小.可以看出,当逃逸脉冲方向偏差为5°和10°时,造成追踪方最优消耗的偏差不超过0.2 m/s,当逃逸脉冲方向偏差为20°时,造成追踪方最优消耗的偏差不超过1 m/s,这表明追踪方的最优消耗在逃逸方最优逃逸方向附近变化是平缓的,这一点在图4中也可以体现出来.在大量的仿真结果中,均得到了同样的结论.所以我们可以断定,只要生成的逃逸脉冲方向与最优的方向相差不大,那么逃逸是完全有效的,且是近似最优的.
从神经网络输出的结果来看,如图6中表现最好的10个隐藏层、每层256个神经元的网络,在测试集上的输出误差小于5°的准确率为91.87%,小于10°的准确率为97.45%,小于20°的准确率为99.27%,由前述偏差分析可知网络生成的逃逸脉冲方向是对应相对状态下的近似最优,并且准确度很高.

图7 追踪方最优消耗偏差与逃逸方向偏差的关系Fig.7 The deviation of optimum fuel consumption for pursuer in relation to that of the direction of evasive impulse
4.4 可推广能力分析
需考察所训练出神经网络的可推广性,考虑到构建训练样本集时,样本的相对距离与相对速度大小分别是由在10~50 km内与10~35 m/s内,等间隔选取特定值所获得的,选取范围以外的值构建新的测试样本,对训练出的10个隐藏层、每层256个神经元,隐藏层神经元为ReLU函数,输出层神经元为Tanh函数的网络进行再测试,以检验所训练出神经网络的泛化能力,测试结果见表7与表8,表中每一行的结果由2000个新样本测试所得.

表7 新样本测试结果ITab.7 Test results of new samples (I)

表8 新样本测试结果IITab.8 Test results of new samples (II)
可以看到,对于训练样本选取范围以外的新样本,充分训练后的神经网络依然表现出较好的测试效果,这表明本文中所提方法训练出的深度神经网络,具有较好的泛化性能,在反交会逃逸脉冲求解方面具有很好的可推广能力.
最后,在计算时长消耗方面,训练好的神经网络具有绝对的优势:10个隐藏层每层256个神经元的网络计算一次逃逸脉冲只需要0.00021 s,而根据双层数学规划模型用PSO算法求解一次逃逸脉冲需要数十秒,这表明深度学习的方法用于计算逃逸脉冲速度极快,具备实时计算逃逸策略的能力.
综上,经充分训练的深度神经网络,可以高精度地输出近似最优的逃逸脉冲方向,并且具有应对未知样本的泛化能力,计算效率极高,可以线下训练后加载到星上,实现在轨逃逸脉冲的实时快速计算.
5 结 论
针对空间中的近距离非合作交会,提出一种基于深度神经网络的逃逸机动生成方法.建立了描述逃逸场景的双层数学规划模型并使用粒子群优化算法求解,构建样本集,设计并训练了深度神经网络,研究了网络超参数对学习效果的影响,并分析了网络的泛化能力.仿真结果表明,充分训练后的神经网络可以很好地掌握逃逸脉冲生成的规律,具有输出精度高、计算速度快和泛化性能好的优势,可用于航天器在轨逃逸脉冲的实时生成,给轨道博弈中的反交会逃逸提供了一种智能化手段.

