仓储立体库纱锭智能配重打包方法研究

陈家浩，庞爱民，李 浩，方应梅

仓储立体库纱锭智能配重打包方法研究

陈家浩，庞爱民*，李 浩，方应梅

（武汉纺织大学 机械工程与自动化学院，湖北 武汉 430200）

传统纱锭配重打包大多由人工完成或者由机器完成部分工序。人工重复工作易疲劳，打包效率低，并且纱锭重量误差大。无法满足纱锭交易市场要求的重量控制在较小误差范围。本文研究一种纱锭配重组合打包的立体库方法，首先在传统纱锭流水线基础上优化，设计出立体仓储提高库存与利用率。对纱锭流水线动态称重后跟踪出入库，利用配重相关理论和智能算法，将纱锭分拣配重打包，实现纱锭动态运输。针对人工配重精度不高的问题，通过比较现有的重量组合法，给出改进的回溯配对方法，横向纵向动态遍历仓储中不同重量的纱锭。经过仿真实验表明，改进的智能配重方法能大大提高纱锭配重效率，可实际运用于企业生产中。

纱锭；立体库；智能配重；回溯算法

0 引言

目前市场对纺织品的需求不断增大，纺织企业为适应多变的市场需求，生产规模也在不断扩大。传统仓库的纱锭分拣模式无法满足现在多种类、多颜色、多数目的需求，过大的生产规模会产生很多库存。人工或半自动打包配重耗费人力财力，增加企业成本，无法满足多种类大批量的生产方式。本文提出的智能立体仓库是将传统仓库与计算机结合，通过控制管理纱锭出入库，使较多数量纱锭缓冲达到动态平衡[1]。纱锭受纺织车间温度湿度环境影响，重量轻重不一。人工操控络筒机流水线使得纱锭平均重量有差异，无法达到配重打包误差要求[2]。

纱锭智能配重打包技术今日已十分广泛，不少相关人员都对自动配重打包进行相关研究。德国Neuenhauser公司用托盘包装纱锭[3]，设计出能使纱锭从络筒机到纱锭打包的自动化流程，但是该流程打包机价格昂贵、占地面积大。秦岭对纱锭输送方式进行分析[4]，设计出多品种纱锭的分拣装置，但没有对整包纱锭实现重量控制。谢楠等[5]采用下料、输送、打包、码垛等工序对纱锭包装控制，但是没有控制对整包纱锭重量的分析。Kim等[6]采用排序算法和聚类算法结合的方式应用于智能仓库货物分拣和最短路径优化。目前国内外缺少针对较多数量纱锭自动配重打包系统的方案，本文为解决纱锭自动配重打包分拣效率低下、分拣过程复杂的问题。设计一种立体库智能配重系统，可有效解决人工配重费时费力问题，显著提高分拣效率，并能根据纱锭工艺流程要求自动调节分拣时间，大大提高企业生产效率。

1 仓库智能配重方案设计

纺织市场对纱线打包质量要求越来越高，传统配送系统较难满足实际需求。本文设计了纱锭全自动配重打包系统，实现了纱锭从取料、运送、检测分拣、称重打包全自动过程。系统工作流程如图1所示。由络筒机、吹尘机构、检测机构、分拣机构、配重系统、仓库调度系统、码垛打包系统组成[7]。

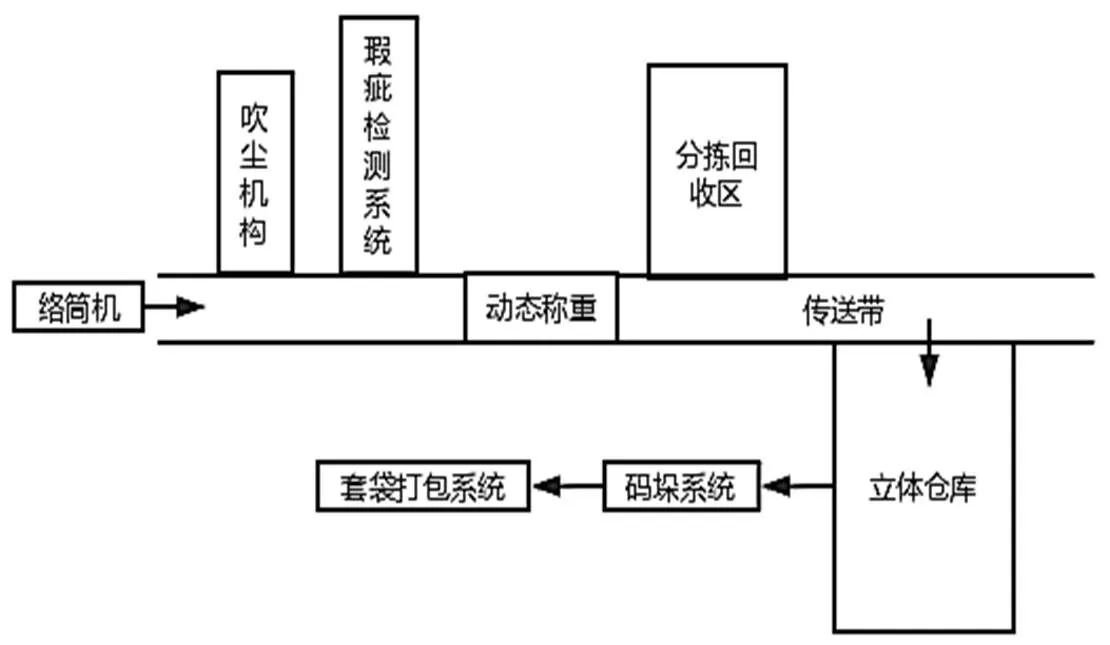
图1 纱锭自动配重打包流程图

纱锭自动配重打包的工作流程为：当纺纱机完成缠绕纱锭后，纱锭经下纱机构排列放置在生产传送线上。吹尘机构从四周排气，降低粘黏在纱锭上的粉尘等杂质。通过检测系统判断单个纱锭颜色、瑕疵，由动态称重系统对每个纱锭称重记录并套袋标签。上位机识别纱锭种类，如果异常则分拣。码垛机器人将检测套袋后合格的纱锭依次入库，实现立体仓库缓存。配重系统匹配合适重量的纱锭出库，使整包重量满足要求。最后打包系统将薄膜覆盖并热熔塑封，纱锭套袋。

2 纱锭配重方法

2.1 配重原则

根据纺织企业要求，单个纱锭平均重量m= 3.125kg，与平均重量相差5%以内都可算合格的纱锭，合格纱锭重量区间为（2.969kg，3.281kg）。按8个纱锭打包成整包，完成整包纱锭包装后总重量为M=25kg，误差为总重量的1%即δ=250g。整包纱锭在打包后总重量在误差范围内，应市场需求总重量合格范围为[M-δ,M+δ]，δ为误差精度。

2.2 纱锭排列组合算法

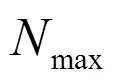
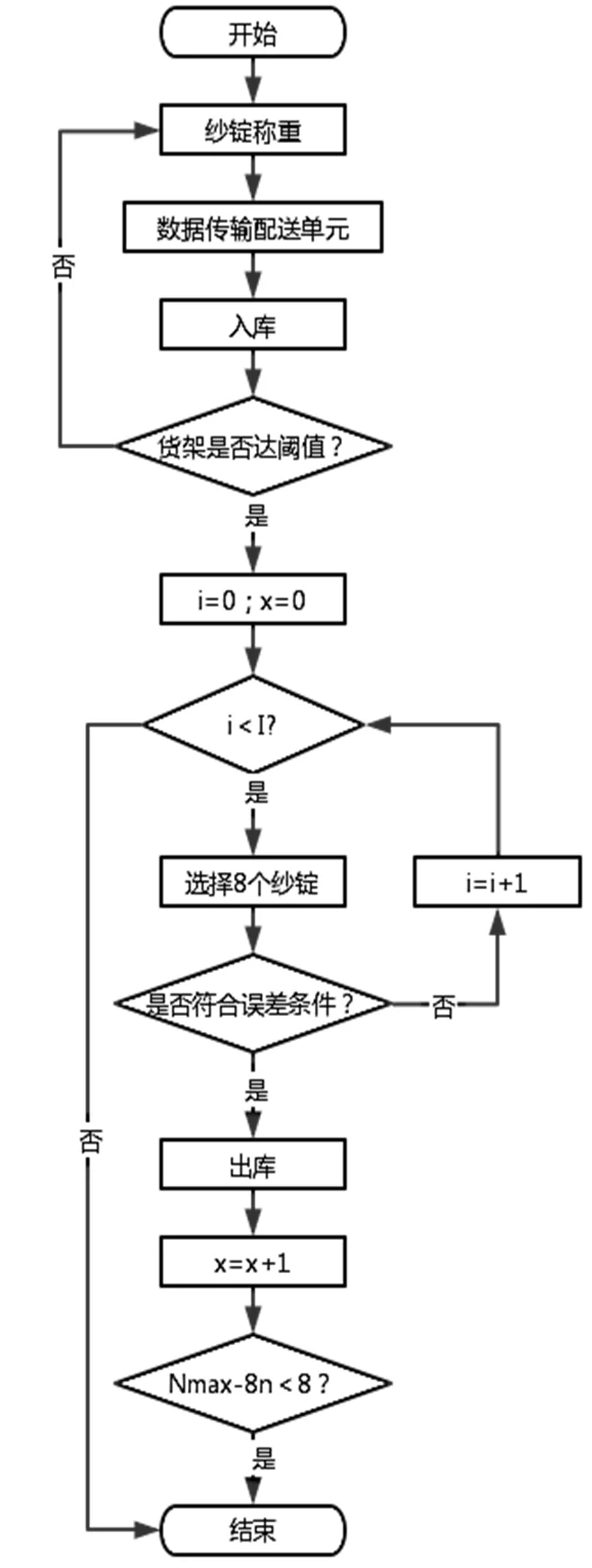
图2 纱锭组合排列法流程图

2.3 重量配对法

纱锭数组直接排列组合复杂度非常高，在实际操作中纱锭组合成功率低；组合时间长，故不采用此方法而是采用轻重纱锭配对的方法。首先将仓库中的纱锭由小到大排序，由于数据规模较大，数组不断变化且没有确定值，所以采用速度最快的快速排序算法。快速排序算法的思想是选择一个基准，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面。通过一次快速排序将排列数据分割成独立两部分，其中一部分所有数据都比另外一部分所有数据都小。再按此方法对两部分数据分别快速排序，以此达到整个数组都变成有序数组。后来的入库纱锭数组则直接插入在有序数组中。然后将纱锭按给定区间分类，纱锭的合格重量区间为（p，q），重量比p小的统称较轻纱锭，重量比q大的统称较重纱锭。

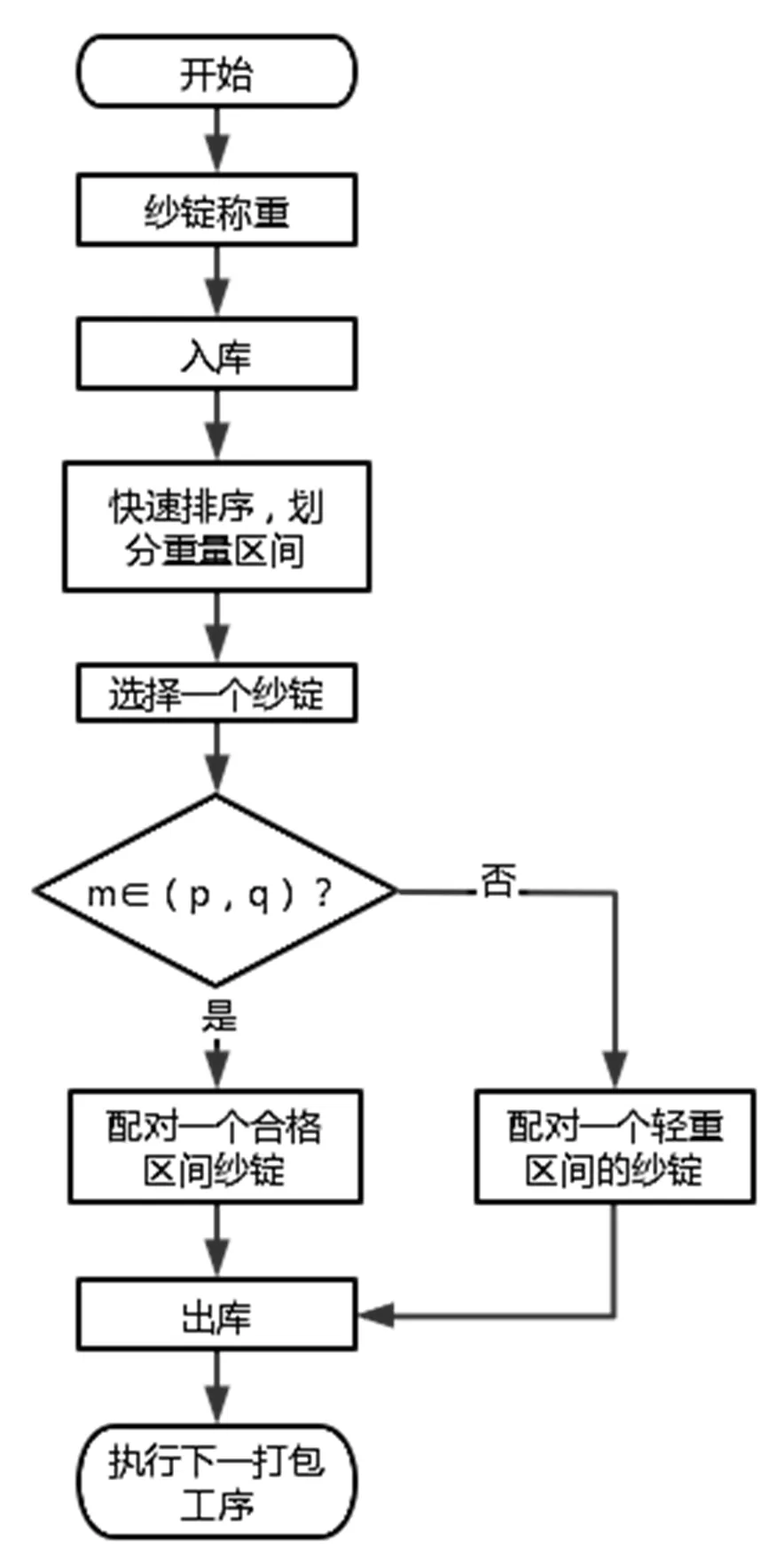
图3 重量配对法流程图

将排序好的纱锭按重量分若干个区间（p-nr，p-（n-1）r）,（p-(n-1)r，p-（n-2）r）…（p，q）…（q+（n-2）r，q+（n-1）r）（q+（n-1）r，q+nr）。其中r表示区间间隔，n表示分的区间数[9]。如果选出的第N个纱锭是合格区间的纱锭，则选择第N+1个纱锭是也为合格区间的纱锭；如果选出的第N个纱锭是较重区间的纱锭，则第N+1个纱锭时要从较轻的对应区间选择，保证轻重纱锭两两配对。将仓库中的纱锭每2个配对一组，选择每4组纱锭轻重中和，误差较小的打包成一袋。采取重量配对法优点是算法复杂度低，配对速度快。缺点是无法保证轻重区间的纱锭能一一对应，会剩余较多或轻或重的纱锭无法配对[10]。

运行流程图如图3所示。

2.4 改进的回溯配对算法

改进的回溯配对算法的基本思想是[11]，按照区间顺序依次确定每个纱锭的重量，按要求把8个纱锭打包成一包，可假定成8个空位置。首先为第一个空位置选择满足约束条件的第1个纱锭数据，即N=1。然后再为下一个位置确定合适的纱锭数据，以此类推，直到确定了所有纱锭位置。在这一过程中，可能会出现这样的情况:即无法为第N个位置找到满足约束条件的纱锭数据。这说明其前面已放置纱锭数据需要进行调整，因此可以先考虑将第N-1个位置选择一个满足约束条件的纱锭数据，如果第N-1个位置无法寻找到一个满足约束条件的纱锭数据，则可以进一步向前调整第N-2个纱锭的数据，以此类推，之后再为第N个空位置寻找满足约束条件的纱锭数据。以这样的方式进行下去，最终可以保证所有纱锭总重量在误差范围内。运行流程如图4所示。

假设第一个空位置选择的是轻纱锭，第二个空位置则选重纱锭，一直到给定的第N个位置。判断前N个纱锭平均重量是否偏轻，如果前N个纱锭平均质量比标准纱锭重量轻，再为第N+1个空位置选择较重区间的纱锭，按一轻一重的模式依次确定各位置的数值，直到所有位置都满足约束条件要求。如果找不出第N+1个符合要求的纱锭，则说明第N个纱锭误差过大不能进行配对，从相邻区间重新选择纱锭[12]。

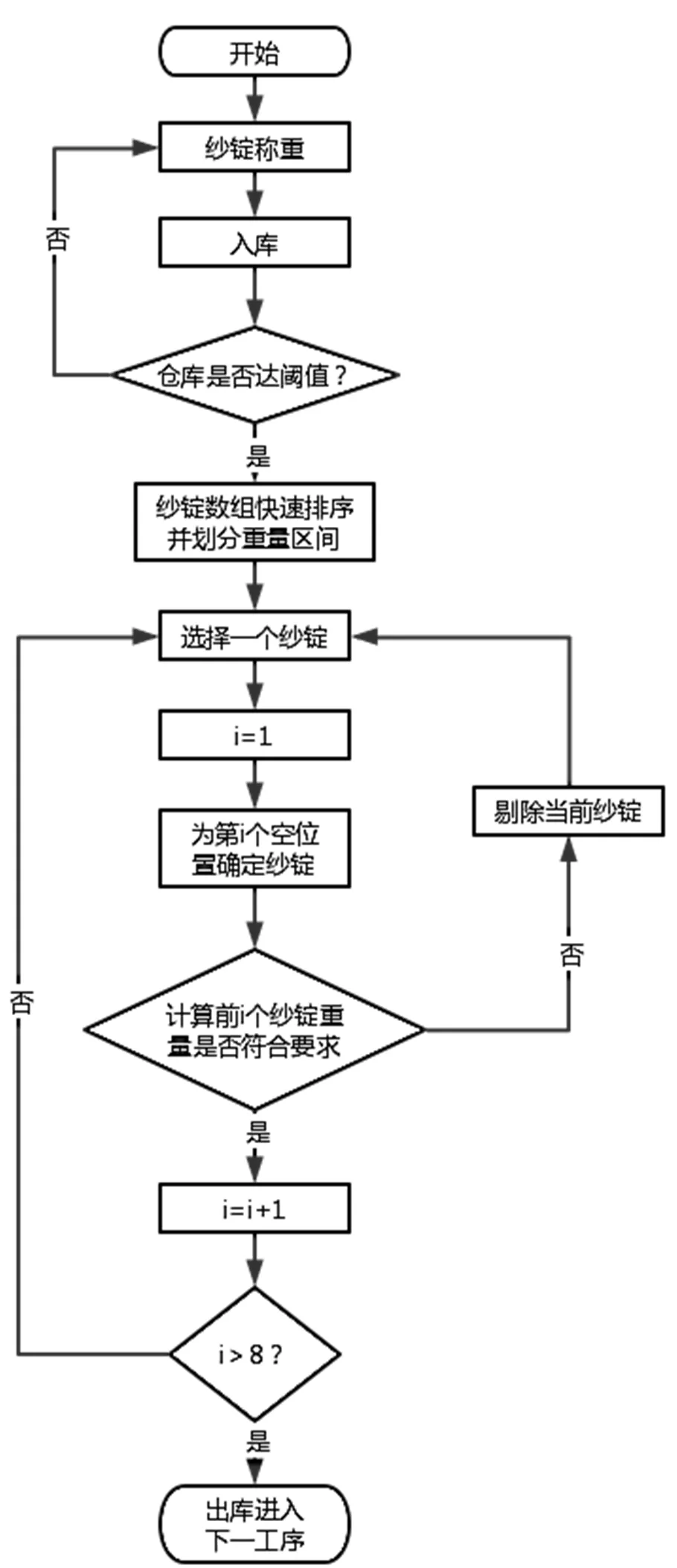
图4 回溯配对法流程图

使用回溯法解决纱锭配重问题的步骤如下所示:

（1）针对所给问题，定义问题的解空间：配重问题的解空间为所有能满足误差的纱锭数据组合。

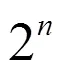
（3）确定搜索方式：以深度优先方式递归地搜索解空间，并且在搜索过程中使用剪枝函数避免无效搜索，提高搜索效率[13]。

其中，我们需要横向的遍历（即第一个数据从1，2，3，4······k挨个寻找），还需要纵向的遍历（添加第一个空位置，···，直至第n个空位置），每一层的纵向遍历都需要经历横向搜索。k代表横向长度，n代表纵向深度。

3 实验结果分析

为验证设计的配重方案的可行性，针对多个不同规模的仓库库存，由改进的配重算法给出最优组合方案。实验数据如下：根据某企业随机两批生产的1000个纱锭重量为实验对象，纱锭重量区间如图5直方图所示。

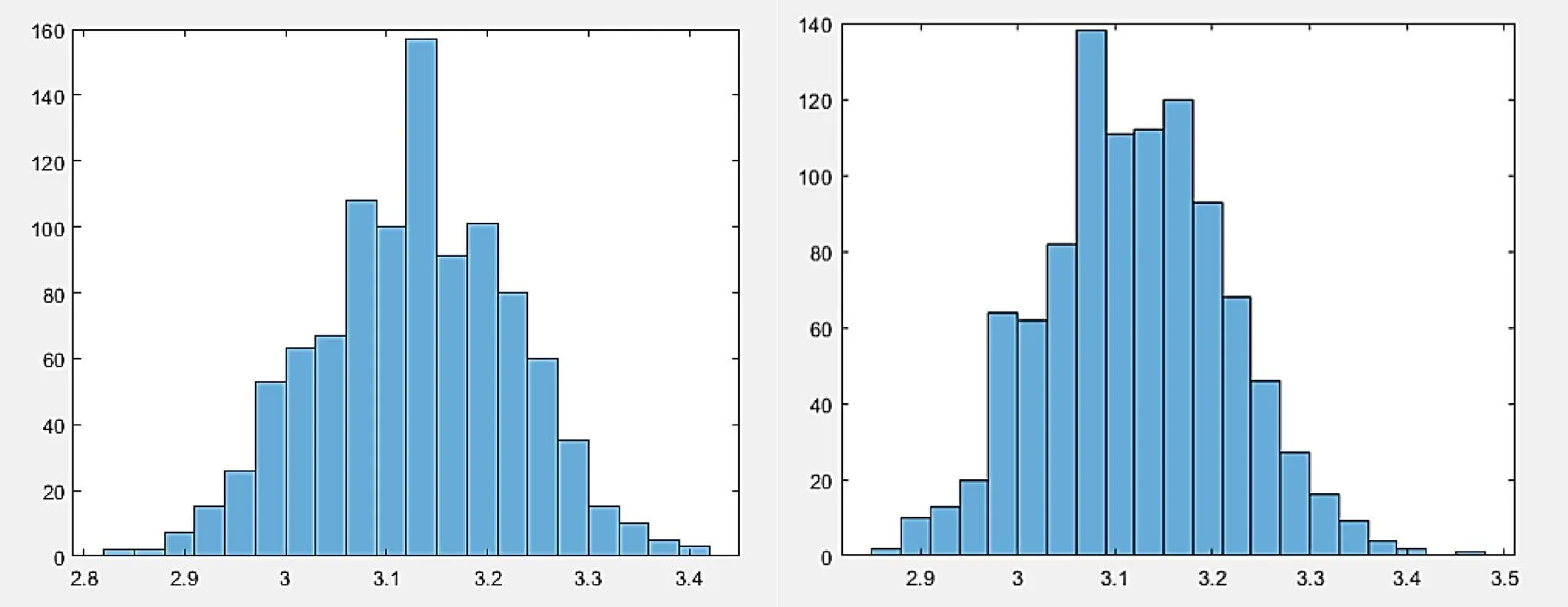
图5 纱锭重量分布直方图

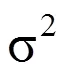
为了直观地体现算法的配重组合能力，本文提出配合组合比率的评价指标，其配重比率R的计算方法：

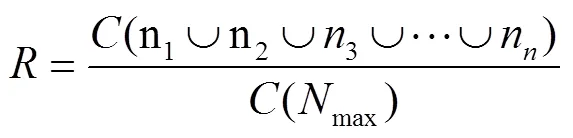
其中，n表示打包成功的纱锭数；N表示总的纱锭库存数。把组合排列算法记为方法1，重量配对法记为方法2，改进的回溯配对法记为方法3。将数据输入配重程序，经仿真实验得到的配重比率表1所示：

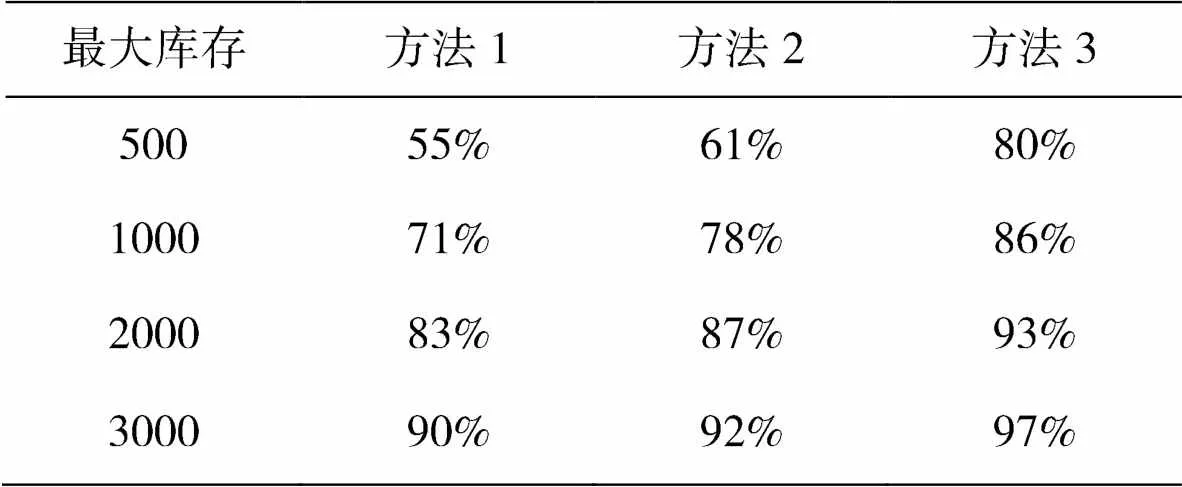
表1 不同方法配重比率

根据表中结果可知，配重算法对纱锭配重效率影响较大，其中方法3的配重效率最高，达到80%。说明改进的回溯配重法针对仓库出入库的纱锭配重有很好的效果。当出现配重率低的情况，可以通过增大仓库库存量缓解。

4 结语

本文在分析国内外纱锭配重环节现状与问题的基础上，结合现阶段的市场需求，提出了一种自动配重运输打包的智能仓库系统，确定了配重方案和配重组合算法，使整包纱锭重量控制在较小误差范围内。通过理论分析和实验仿真，结果表明配重比率趋于稳定且配对成功率达97%。相较于人工配对，算法配对大幅提高生产效率，降低成本。设计的纱锭立体仓库流程能自动高效地完成出入库配重套袋的工作，从根本上解决企业配重的技术难题，具有很好的应用前景。

[1] 刘晓燕, 方玉林. 纺纱智能化关键技术及应用效果[J].棉纺织技术, 2016, 44(08): 79-81.

[2] 杨伟. 筒子纱自动包装系统设计方案分析[J]. 工业设计, 2015, (11):136+148.

[3] 张文丽. 基于自动配重的筒子纱包装系统的研究与设计[D]. 武汉：武汉纺织大学, 2017.

[4] 秦岭. 筒子纱自动输送系统的设计与开发[D]. 济南：山东大学, 2016.

[5] 谢楠. 筒子纱自动包装与码垛系统设计与开发[D]. 天津：天津工业大学, 2017.

[6] Byung-In Kim, Sunderesh S Heragu, Robert J Graves, et al. Clustering-based order-picking sequence algorithm for an automated warehouse[J]. International Journal of Production Research, 2003, 41(15).

[7] 刘晓龙. 全自动筒子纱打包机的关键技术研究[D]. 南京：东南大学, 2020.

[8] 彭来湖, 祝孝裕, 张少民, 等. 筒子纱包装自动配重方法研究[J]. 纺织学报, 2020, 41(06):147-152.

[9] 殷罡, 彭军强. 筒纱自动输送打包系统自动配重方法研究[J]. 纺织导报, 2021, (06): 59-61.

[10] 张华龙. 全自动筒纱包装生产线的设计与实现[D]. 济南：山东大学, 2015.

[11] 李楷, 陈永府, 金志勇, 等. 基于回溯法的全覆盖路径规划算法[J]. 计算机工程与科学, 2019, 41(07): 1227-1235.

[12] 祝孝裕. 筒纱包装自动化生产线控制技术研究[D]. 杭州：浙江理工大学, 2019.

[13] 杨超, 何书前, 郑志群, 等. 回溯法与分枝限界法的分析与比较[J]. 电脑知识与技术, 2018, 14(11): 44-46.

Research on the Method of Intelligent Weighing and Packing for Three-Dimensional Warehouse

CHAN Jia-hao, PANG Ai-min, LI Hao, FANG Ying-mei

(School of Mechanical Engineering and Automation, Wuhan Textile University, Wuhan Hubei 430200, China)

Most of the Baling of traditional spindles are done by hand or by machine. Manual repetitive work is easy to experience fatigue, low packing efficiency and large spindle weight error. The weight which can not meet the requirements of the spindle trading market is controlled in a small error range. In this paper, a method of three-dimensional storage for combined packing of spindles is studied. Firstly, on the basis of the traditional assembly line of spindles, the three-dimensional storage is designed to improve the stock and utilization ratio. According to the theory of balance weight and the improved algorithm, the dynamic transportation of spindle is realized by packing and sorting the balance weight. In order to solve the problem of low precision of manual counterweight, an improved backtracking matching method is given by analyzing and comparing the existing weight combination method. The simulation results show that the improved intelligent weighting method can greatly improve the efficiency of spindle weighting, and can be used in enterprise production.

spindle; storage three-dimensional library; intelligent counterweight; backtracking algorithm

庞爱民（1968-），女，教授，硕士，研究方向：智能制造，纺织机械.

TP242.2

A

2095－414X(2022)05－0046－05