参数竞争风险分位数模型

胡军浩，黄荧，杨青

（中南民族大学 数学与统计学学院，武汉 430074）

竞争风险是指一个研究对象会发生多个结局事件，并且一个结局事件的发生会影响其他结局事件发生的概率，这些结局事件间便存在竞争风险.竞争风险模型作为一种处理具有多种潜在结局生存数据的分析方法，在临床医学、流行病、经济学等领域的研究中越来越重要.1992年，WEI将线性回归模型的建模方法引入生存分析领域，提出了相较于经典的COX比例风险模型更加简单、直观且易于理解的AFT模型［1］.1999年，FINE和GRAY基于累积发生函数和特定失败类型的边际风险概率，提出了一种能直接解释特定终点生存概率的子分布比例风险模型［2］，其准确性和可靠性引发了广泛的研究兴趣.2009年，PENG和FINE将分位数回归引入到竞争风险设置中，并建立了一个竞争风险分位数回归模型［3］，使得协变量效应能够得到合理解释.该模型扩展了AFT模型，为子分布比例风险模型提供了一个有力补充，同时也为竞争风险的研究提供了一个新的视角.

传统的竞争风险分位数回归模型采用最小化L1型凸函数的方法来估计其回归系数，然而对不平滑估计函数的最小值问题求解，可能会导致解的不唯一性.同时，一次估计一个条件分位数，不仅估计效率低，而且估计结果难以解释.文献［4］通过计算标准高斯随机扰动上的期望值，得到不平滑估计函数的平滑近似，文献［5］利用核光滑方法，对竞争风险下的累积发生函数光滑化，进行光滑估计方程的非参数估计.受文献［6］的启发，本文将系数函数参数化建模的思想，应用到竞争风险分位数回归模型中，建立了一个参数竞争风险分位数模型，并分析了其估计量的渐近性质，给出了模型选择过程，最后，通过仿真模拟和实际数据对模型进行评价和实现.

1 竞争风险分位数回归模型

设T为感兴趣的生存时间，可能受到删失C的影响，∈={1，…，K}表示失败的原因，Z是第一维恒为常数1的p+1维协变量向量.观察到n个独立同分 布 的 样 本{(Xi，δi，Zi)，i=1，…，n}，其 中X=min(T，C)，δ=I(T≤C)∈.存在一个与T相关的潜在时间变量，原因k下的生存时间T*k=I(∈=k)×T+I(∈≠k)×∞.基于累积发生函数，定义Tk*的条件分位数：

为便于后续讨论，其他事件存在的情况下，仅对原因1事件的发生感兴趣.对于τ∈[τL，τU]，0＜τL，τU＜1，广义线性竞争风险分位数回归模型为：

其中β(τ)为p+1维未知回归系数向量，g(·)是一个已知的单调连接函数.

当竞争风险数据不存在删失时，即X=T，δ=∈，可直接通过最小绝对偏差方法来估计系数.β(τ)最小化目标函数为：

也可以表示为相应梯度函数的零点：

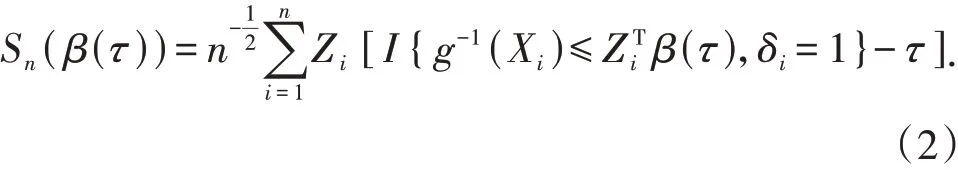
当竞争风险数据存在删失C时，假设在给定协变量Z下，删失时间C条件独立于生存时间T.文献［3］采用删失加权的逆概率方法，得到调整后的加权估计方程：

2 参数竞争风险分位数模型

考虑为模型（1）中的系数函数β(τ)引入一个有限维参数θ，定义：

其中b(τ)=[1，b1(τ)，…，br(τ)]T为τ的r+1维已知函数向量，θ是元素为θjh，j=0，…，p，h=0，…，r的(p+1)×(r+1)维矩阵，指定j=0，h=0分别表示Z和b(τ)的常数项.第j个协变量Zj对应的回归系数为βj(τ|θ)=θj0+b1(τ)θj1+…+br(τ)θjr，j=1，2，…，p.

由此定义参数竞争风险分位数模型如下：

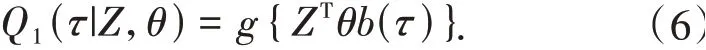
模型（6）可以通过控制θ的一些元素为0，来实现对部分系数函数的参数化，或参数化为b(τ)的子集函数.例如：假定系数β1与b(τ)的常数项无关，β2不参数化，指定系数函数由二次多项式建模，b(τ)=[1，τ，τ2]T，因此设置θ3×3，其中θ10=θ20=θ22=0.估计的分位数函数Q1(τ|Z，θ^)关于τ的一阶导数小于零，则会发生分位数交叉，文献［7］利用一种强制单调性的约束优化算法解决了分位数交叉问题，并在R软件qrcm包中得以实现.在确保模型不发生分位数交叉的前提下，b(τ)可以灵活选择，文献［8］中给出了更多参数函数的例子.

由于竞争和删失的存在，大的分位数可能无法识别.本文在分位数区间[τL，τU]上，将文献［6］提出的积分损失最小化（ILM）方法，应用于模型（6）的参数估计过程.估计为如下积分梯度函数的零点：

其中τi=F1(Xi|Zi，θ)为θ下原因1的累积发生函数.类似地，结合式（3）与式（7），得到删失数据下的积分梯度函数：

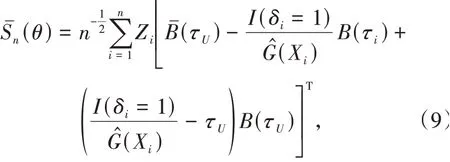
式（8）和式（9）均为θ的平滑估计函数，可通过Newton Raphson方法或文献［9］提出的梯度搜索法进一步求解，有效避免了不连续函数的系数估计过程.与文献［3］一次估计一个分位数对应的回归系数不同，本文通过引入参数，找到了分位数与回归系数之间连接的桥梁，允许一次估计整个分位数过程，在进行平滑估计的同时，极大地提高了估计效率.同样的想法也被延伸到删失和截断数据的分位数回归［10］、纵向数据的分位数回归［11］.进一步地，文献［12］在分位数框架下，讨论了协变量和参数规格均为非线性的情况，是对系数函数参数化建模方法的一个很好的发展.

3 渐近性分析

引理1［13］在独立同分布的数据下，Θ为紧集，a(Zi，θ)在每个θ∈Θ上连续的概率为1，且存在d(Z)，对所有θ∈Θ，都有‖ ‖a(Z，θ)≤d(Z)，E[d(Z)]＜∞，则可得到E[a(Z，θ)]是连续的，且

定理1若满足如下条件：

（i）Θ为紧集；

（ii）存 在 一 个 正 数v，有P(C=v)＞0，P(C＞v)=0；

有界；

（iv）Z，B(τ)，Bˉ(τ)均为一致有界；

证明条件（ii）和条件（iii）为独立删失数据的分位数回归中的标准假设，且根据拉格朗日中值定理易证得为θ的连续函数，从而在每个θ∈Θ上连续的概率为1，这也意味着b(τ)为定义良好的连续函数.在条件（iv）下，可知积分梯度函数一致有界，即：

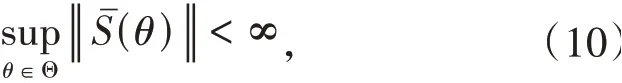
结合条件（i）和引理1，则可知Sˉ0(θ)连续，且：

再根据式（10）和式（11），可得：

对任意ε＞0，由式（12）可得：

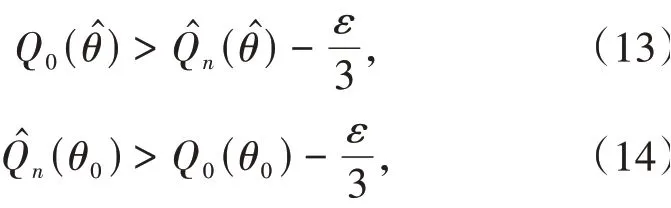
因此结合式（13）～（15），对任意ε＞0，有：

设N为任意包含θ0的Θ的开子集，则Θ∩Nc为紧集.结合条件（v），有：

即Q0(θ)在θ0处取得唯一最大值，对于θ~∈Θ∩Nc，则有：

定理2在满足定理1的条件下，若满足如下条件：

（i）θ0为Θ的内点；

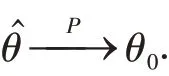
（v）Z和b(τ)均 为 非 奇 异 的.对 于G=则有渐近正态性：

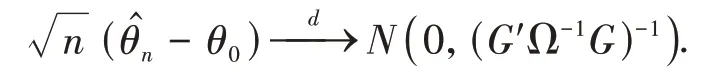
证明类似于文献［13］的证明思想，在大样本中估计量近似等于样本均值的线性组合，由中心极限定理可得到渐近正态性.根据条件（i）和（ii），一阶条 件 满 足的 概 率 接 近1，其 中为Hessian矩阵.在一阶条件下，利用拉格朗日中值定理，在θ0周围扩展并乘以得到：

条件（v）意味着G为满秩矩阵，结合逆矩阵的连续性，由式（20）得到：

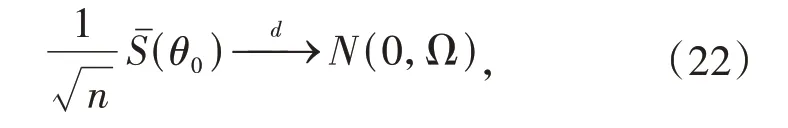
通过Slutsky定理，证得估计量的渐近正态性：

4 拟合优度测量

文献［14］和文献［15］均指定累积发生函数为特定的分布，提出了竞争风险场景下的拟合优度程序，然而关于参数竞争风险模型的拟合优度测量目前没有一个正式的数值检验方法.评估式（4）的最小值意味着对数据整体拟合优度情况的度量，式（4）的值越小，模型与数据的拟合情况越好［16］.式（4）的最小值类似于似然函数的最大似然值，据此，本文结合式（4）与信息准则提出参数竞争风险分位数模型的拟合优度评估过程.使用文献［17］提出的AIC信息准则的调整版本：

和文献［18］提出的BIC信息准则的调整版本：

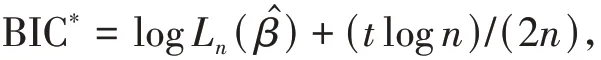
5 数值模拟

5.1 仿真数据生成

设置协变量向量Z=(1，Z1，Z2)T，其中Z1由标准均匀分布随机生成，Z2由概率为0.5的伯努利分布随机生成.两个相互竞争的失败原因为∈=1和∈=2，原因1发生的概率满足P(∈=1|Z)=p0I(Z2=0)+p1I(Z2=1).生存时间服从条件分布P(T≤t|∈=1，Z)=Φ(logt-γTZ)，P(T≤t|∈=2，Z)=Φ(logtαTZ).删失时间C服从(0，cu)上的均匀分布，通过点cu来控制删失率.在上述设置下，对于τ∈[0.1，0.4]，潜在的竞争风险分位数模型可以描述为：

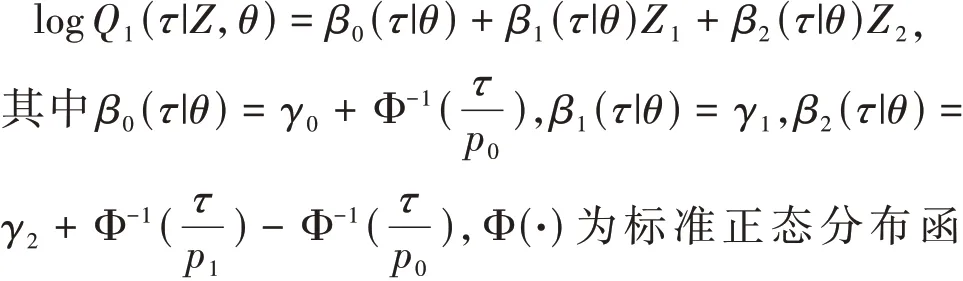
分别在两个样本容量n=100，n=200下，设置两个不同的模拟场景.场景1：cu=5，p0=0.8，p1=0.6，a0=(1，0，-0.5)T，γ0=(0，0，-0.5)T，该 场 景下大约有20%的个体发生删失，55%的个体失败于原因1，25%的个体失败于原因2.场景2：cu=7.6，p0=0.8，p1=0.6，a0=(0，0.5，-0.5)T，γ0=(0，-1，-0.5)T，该场景下大约有10%的个体发生删失，60%的个体失败于原因1，30%的个体失败于原因2.

5.2 参数估计量的有限样本性质

为评估估计量的有限样本性能，通过800次蒙特卡罗模拟，比较参数估计量β^n(τ)=β(τ|θ^n)与竞争风险分位数模型中估计量β^n(τ)的偏差和标准误，两个估计量的偏差均很小，不作报告，标准误的测量结果如表1所示.

表1 模拟场景下竞争风险分位数回归模型（CRQR）和参数竞争风险分位数回归模型（PCRQR）的标准误对比Tab.1 Comparison of standard errors of competing risks quantile regression model（CRQR）and parametric competing risks quantile regression model（PCRQR）in simulated scenarios

仿真实验结果表明，参数竞争风险分位数模型在不同场景、不同样本量下，估计的标准误都要低于传统的竞争风险分位数回归模型，在较大的分位数下优势更明显.与期望的结果相同，参数结构下的竞争风险分位数模型有更好的性能.

6 真实数据分析

将参数竞争风险分位数模型应用到文献［19］有关滤泡细胞淋巴瘤疾病的研究数据中.该数据集由541名疾病早期的滤泡淋巴瘤（I或II）患者组成，接受单纯放疗（化疗=0）或放疗和化疗的联合治疗（化疗=1）.疾病复发或对治疗无反应和缓解期死亡为两个结局事件，实验对疾病复发或对治疗无反应（RNT）这个结局事件感兴趣，缓解期死亡事件视为它的竞争事件.患者的年龄（age：平均=57），血红蛋白水平（hgb：平均=138）也被记录.其中有272个感兴趣的事件、76个竞争风险事件和193个删失事件.首先对实验数据进行预处理，将协变量分别表示为Z1：年龄/10，Z2：血红蛋白/100，Z3：临床阶段，Z4：治疗方法.用如下参数竞争风险分位数模型描述RNT事件的生存时间：

为了使模型更好地拟合数据，根据第4节提出的拟合优度测量过程，首先对b(τ)的规格进行选择，不同规格下模型的拟合优度评估结果如表2所示.

通过系数函数图像进行模型的初步筛选后，表2列出了7个不同规格指定下，模型所含的参数个数及AIC*值、BIC*值.模型1和2指定b(τ)为τ的幂函数形式.模型3指定为τ的指数函数形式，该模型涉及参数较少，但从AIC*，BIC*的值来看，模型与数据的拟合效果不理想.模型4和模型5分别使用了非对称逻辑分布和三角分布的分位数函数，相比前面的模型，它们拥有较少的参数数量，且拟合效果也是比较令人满意的.基于上述模型的表现，幂律分布、逻辑分布和三角分布应该被考虑，据此指定了模型6.模型7是对模型6的进一步调整，虽然涉及参数个数较多，但其AIC*和BIC*的值相较于其他模型来说更小，拟合情况是让人满意的.选择模型7为最终模型，其参数的估计结果及估计标准误如表3所示.

表2 拟合优度测量Tab.2 Goodness-of-fit measures

表3 模型7的参数估计结果Tab.3 Parameter estimation results for model 7

表3的最后一列为协变量零假设检验的显著性，类似的，最后一行为b(τ)分量零假设的P值，*号表示显著性的程度（括号中为标准误）.由表3的结果得到系数函数的表达式，例如截距项对应的估计系数函数为：

协变量血红蛋白水平对应的估计系数为：

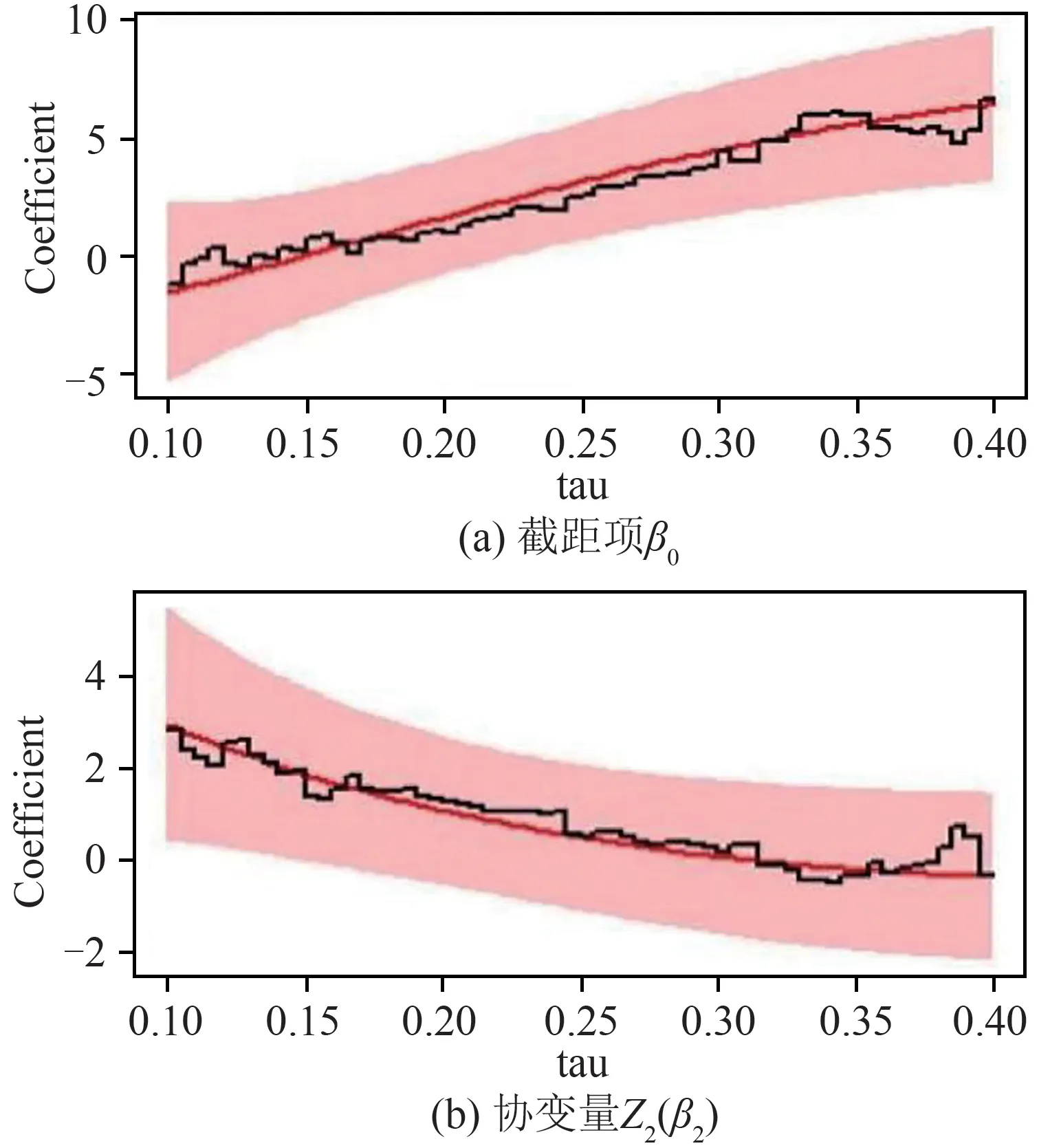
图1 模型7中截距项和协变量Z2对应的回归系数函数Fig.1 Regression coefficients functions corresponding to the intercept and covariate Z2 in model 7

7 结论

参数竞争风险分位数模型是对竞争风险分位数回归模型［3］的发展与改进，不仅解决了非平滑系数估计函数产生的多重根问题，而且在参数结构下有着简单、高效和易于解释的优点.本文构建了参数竞争风险分位数回归模型，给出了积分损失最小化方法下的参数求解过程，其估计量满足一致性和渐近正态性.通过实验模拟数据集评估估计量的有限样本性能，结果表明：参数竞争风险分位数模型有优于竞争风险分位数回归模型的估计性能.