堰闸孔流公式推算堰流流量应用分析
吴立新 孟小敏 韩 阳
(江苏省灌溉总渠管理处 淮安 223200)
1 理论依据
在水力学和水文资料整编中,堰闸沉溺式孔流的流量一般用下式进行计算:
Q=MBe △Z0.5
假设闸门处在即将提出水面而未出水(如距出水相差0.1cm)的临界状态,这时闸门对水流的阻碍作用微乎其微,所以此时的流态既可以把它看作是孔流,也可以把它视为堰流。因水流具有连续性,当闸门缓慢提升在这两种流态之间过渡时,流量大小不会发生突变,此时用孔流和堰流公式计算出的流量应该相等。用孔流公式来推求堰流流量是完全可以的。也可以这样认为,堰流是孔流的一种特殊状态,是孔流状态下闸门开启高度最大时的情形,换句话说,就是所有的堰流都可以当作孔流来处理。
2 应用实例
下面以一个堰闸站为例,根据江苏省苏北灌溉总渠六垛南闸水文站2003—2005年堰流流态下实测流量76 次(见表1),用孔流公式M=Q/(Be△Z0.5)计算流量系数。该闸共7 孔,弧形闸门,单宽9.05m,闸底为实用堰型,闸底高程-0.35m,其中开启高度e 用上游水头(上游水位与闸底高程的差值)代替。以e/△Z 为纵坐标、M 为横坐标,将76 个点据(见表2)点绘在直角坐标图上,如图1所示。从图1可以看出,点群自上而下呈带状分布,如果从点群中心画一条垂直于横坐标的直线,则此直线与横坐标交点的M 值为6.48。
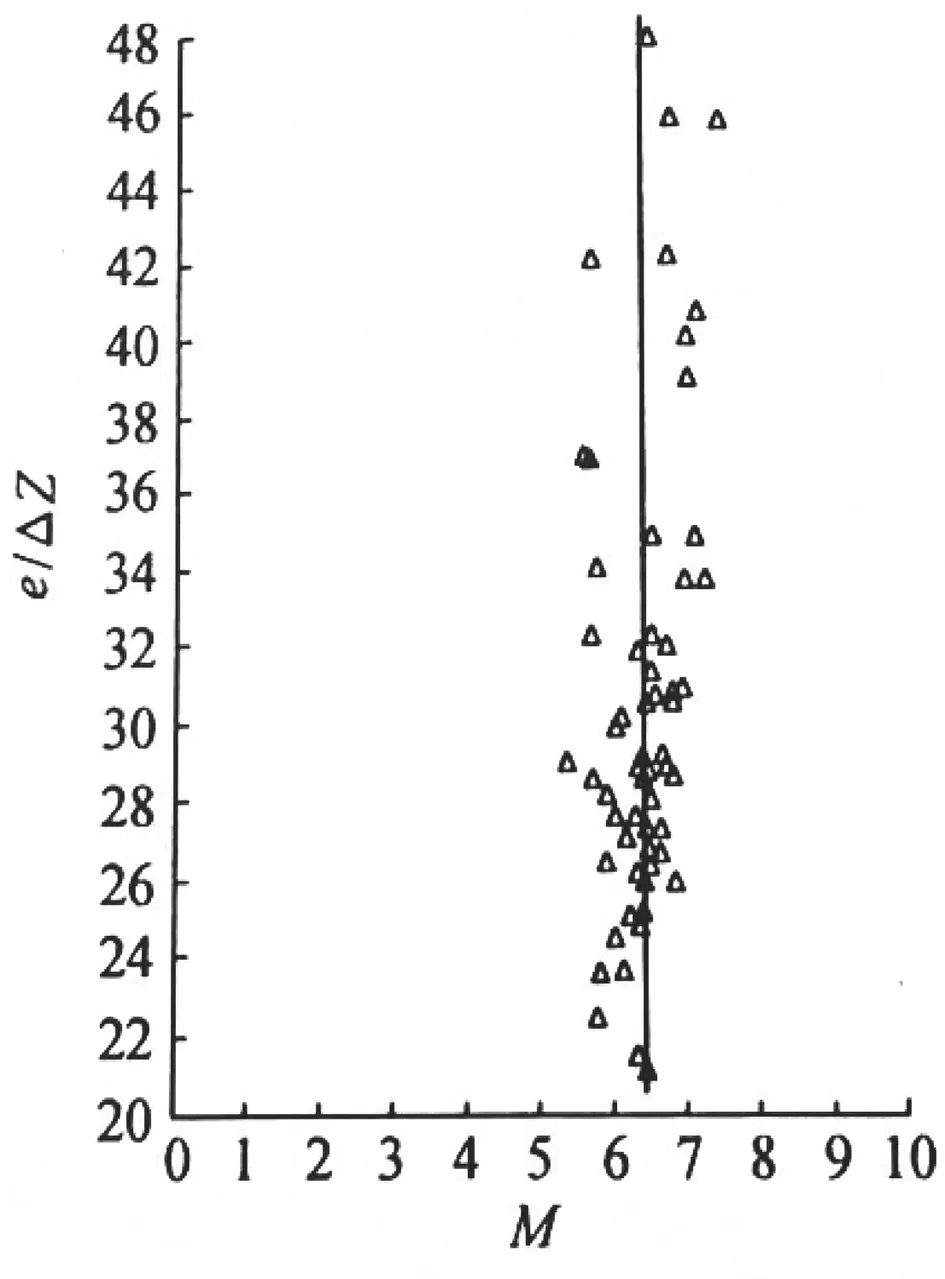
图1 六垛南闸沉溺式堰流e/△Z 的关系图
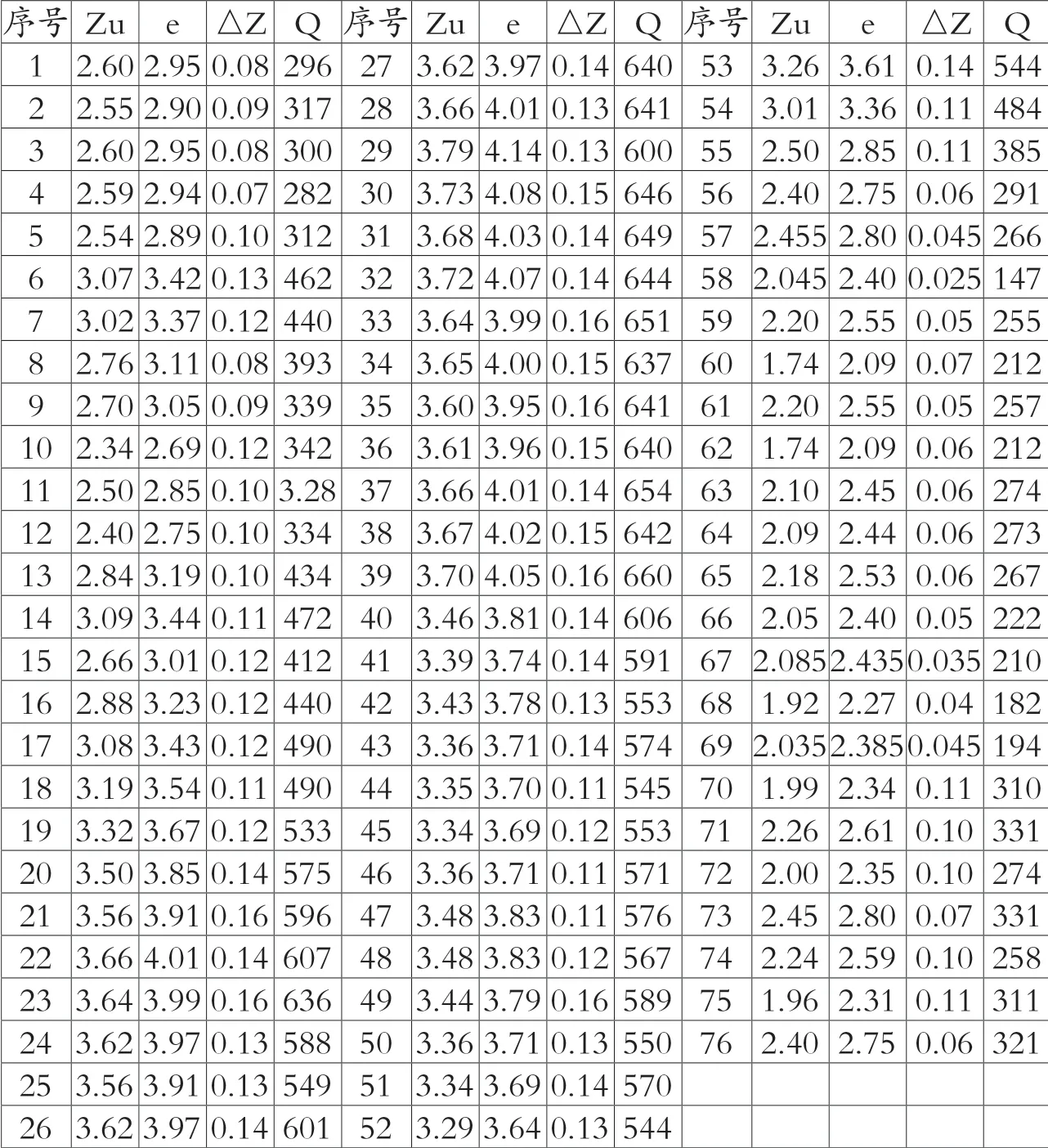
表1 六垛南闸2003—2005年实测流量表
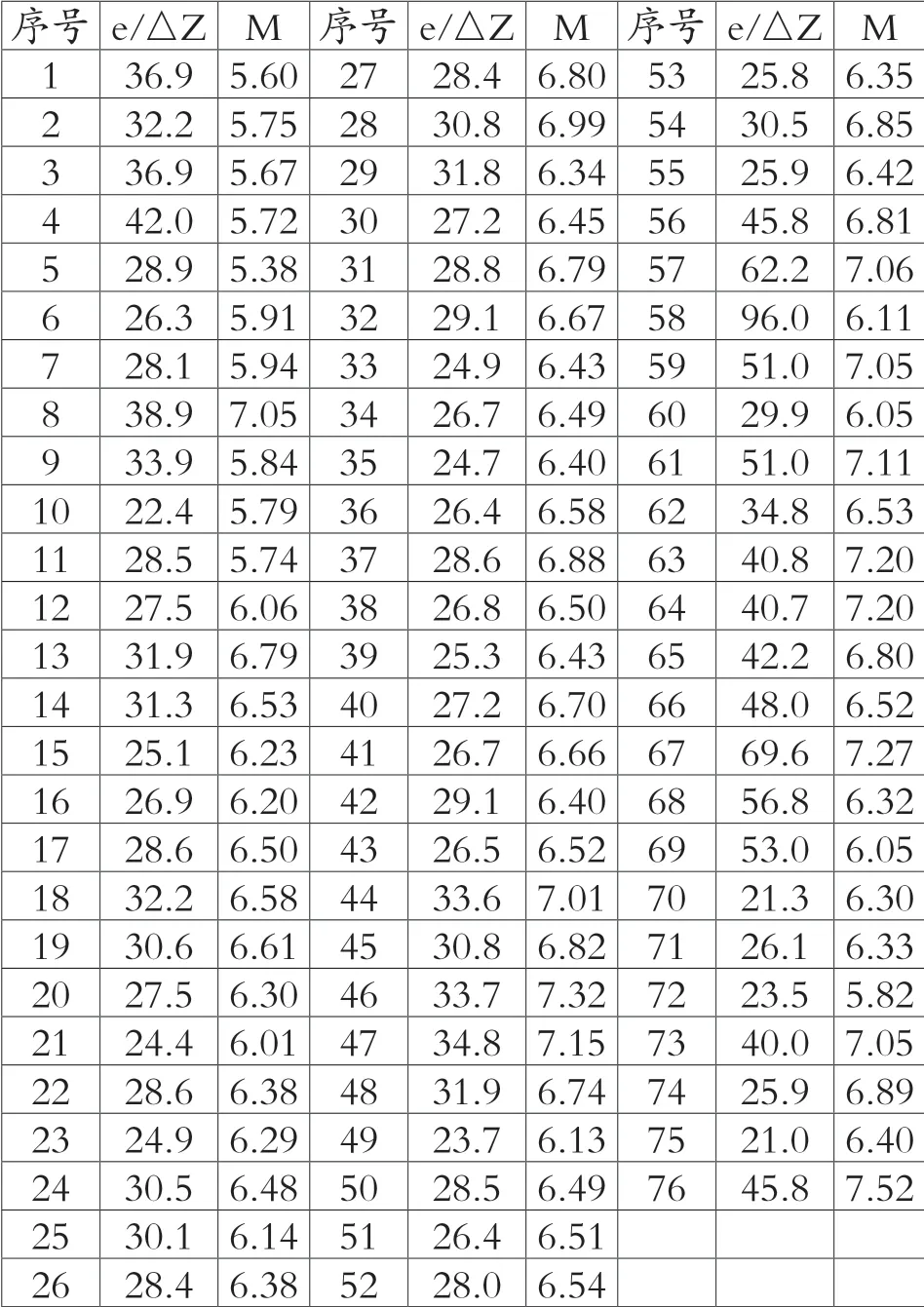
表2 六垛南闸流量系数与水力因子的关系表
3 定线检验和均方差计算
为了验证测点与关系线的拟合情况,根据《水文资料整编规范》(以下简称《规范》)要求,对关系线分别进行符号检验、适线检验和偏离数值检验。
3.1 符号检验
可用下式进行符号检验:
u=(k-0.5n-0.5)/(0.5n0.5)
式中:u—符号检验统计量;k—正号数;n—测点总数。由表3 可知,k=39,n=76。所以:

表3 六垛南闸流量关系线符号检验计算表
u=(39-0.5×76-0.5)÷(0.5×760.5)≈0.11
当α=0.25 时,由《规范》查表得u1-α/2=1.15,因u<u1-α/2,故符号检验合格。
为解决一个问题而读,获得的是一时的参考,广博而有计划的系统阅读是一种长远的眼光,是建立在普遍联系与宏观综合的视野之上的自我锤炼。完善的知识结构将最终决定我们在教育这条路上能够走多远。
3.2 适线检验
可用下式进行适线检验:
u=[0.5×(n-1)-k-0.5]÷[0.5×(n-1)0.5]
式中:u—适线检验统计量;k—变换符号次数;n—测点总数。
将e/△Z 从小到大排序(表4),自上而下统计表中的相对偏差变号次数k=30。

表4 六垛南闸流量关系线适线检验计算表
u=[0.5×(76-1)-30-0.5]÷[0.5×(76-1)0.5]≈1.62
当α=0.05 时,从《规范》查表得u1-α=1.64。因u <u1-α,故适线检验合格。
3.3 偏离数值检验
平均相对偏离值:
P平均=∑(pi-6.48)÷n=2.2÷76 ≈0.029
式中:pi—测点与关系线的相对偏差;n—测点总数;如表5所示。
平均相对偏离值的标准差:
Sp={∑(pi-6.48)2÷[n(n-1)]}0.5
={3622.98÷[76(76-1)]}0.5≈0.80
式中相对偏差平方的累计计算如表5所示。
偏离数值检验公式:
t=P平均÷Sp=0.029÷0.80 ≈0.036
式中:t—偏离数值统计量。
当α=0.20,n=76 时,由《规范》查表得t1-α/2=1.28。因t <t1-α/2,故偏离数值检验合格。
3.4 均方差计算
Se=[∑(pi-6.48)2/(n-1)]0.5
=[3622.98/(76-1)]0.5≈6.95%
4 结论
(1)由3 项检验结果可知,推算结果完全满足《规范》定线要求,实测流量与计算流量的均方差为6.95%,达到二类精度标准。
(2)六垛南闸堰流2003—2005年采用堰流公式定线,由于闸下河床泥沙淤积严重,河床变化较大,关系线每年都在变化,如使用孔流公式,关系线较为稳定,可达到较好效果。
(3)用孔流公式推算堰流流量的优点是:首先是定线简单,平均M 值可直接取各点据M 值的算术平均值,而以往堰流流量关系线为曲线,定线时有很大的任意性。其次是对一般的堰闸,可用公式Q=MBe△Z0.5快速地进行流量估算,对平底闸M 值一般取4~6,对实用堰闸M 取值要略大些。
(4)堰流状态下,闸门是提出水面的,上、下游水位差一般都比较小,小的时候往往只有3~6cm,目前水位的测量技术由于观测误差和水尺零高毫米位的取舍,正常误差都在1~2cm,这会造成小水位差点据散乱较难定线,所以与使用堰流公式定线一样,选一个水位差比较大的流量实测资料来分析,或者提高水位差观测精度,效果会更好■
——以徐州高层小区为例

