基于ADAMS的玻璃传送机稳定性分析
许 博 程小明 王永涛 何 涛
(1.安徽理工大学 机械工程学院,淮南 232001;2.安徽贝可科技有限公司,淮南 232000)
触屏盖板玻璃在高端液晶电视、手机等电子产品中应用广泛。作为液晶面板的必备组件,它是电子交互系统的核心组成部分之一。我国液晶面板产能约占全球总产量的23.7%,在整个液晶面板产业链中具有举足轻重的地位[1-2]。触屏盖板玻璃较薄,且对表面光洁度要求极高。在不同的生产工序中转移时,需要保证触屏盖板玻璃的完整性和传送的高效率,确保液晶面板的安全生产[3-5]。本文设计了一款玻璃传送机,为验证玻璃传送机结构的稳定性,基于机械系统动力学自动分析(Automatic Dynamic Analysis of Mechanical Systems,ADAMS)有限元软件模拟仿真玻璃传送机转动过程中柔性体振动变形的影响,为玻璃传送机的结构优化提供了重要支持。
1 玻璃传送机动力学模型建立
1.1 玻璃传送机结构设计
玻璃传送机装置主要由轴支座、锁紧块、六角轮、玻璃板、梯形槽、支撑条、皮带、固定板、六角轴以及带轮等组成,如图1所示。轴支座安装固定在底架上,用于支撑六角轴等。六角轮串于六角轴。锁紧块用于锁紧固定板,并与六角轮一同完成固定板的支撑与固定。支撑条安装于固定板两侧,梯形槽置在固定板上,两者共同确保玻璃板的滑动,以防脱落。带轮在电机的驱动下带动皮带转动,推动玻璃板朝固定方向滑动。
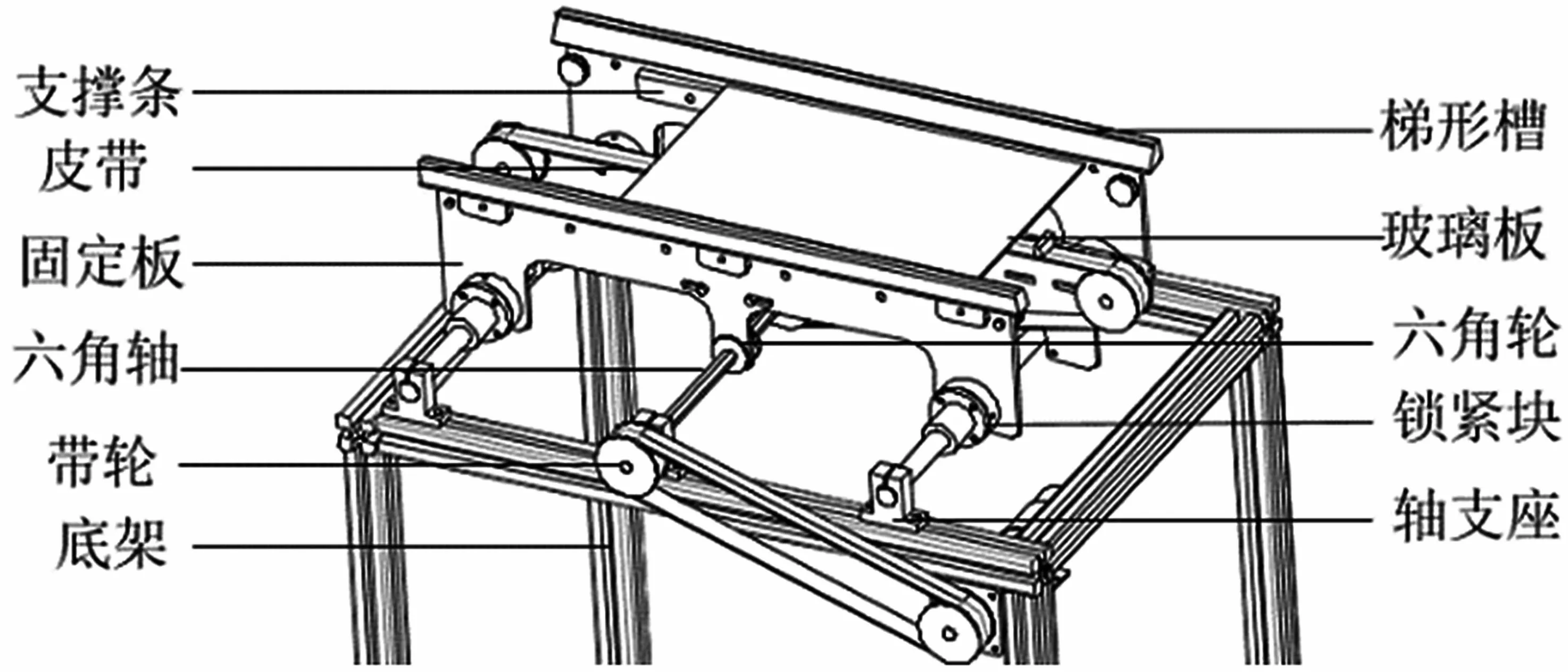
图1 玻璃运输机
1.2 刚柔耦合动力学分析
建立带模型运动假设,将皮带划分为若干单元进行求解,其中各单元参数刚度为Ki,阻尼为ci,质量为mi,运行阻力为fi。若某个单元位移为ui,根据力的平衡方程,使用SolidWorks软件可以得到皮带各单元的力学模型[6-7],如图2所示。
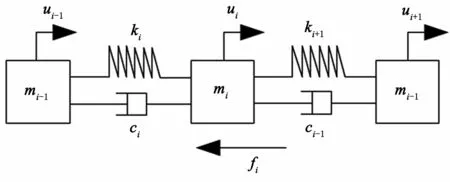
图2 带力学模型
以图3传送机皮带传送为例,皮带全长为L,将皮带均匀划分为7段,承载玻璃板划分为一段,从右侧起始点开始按顺时针编号。
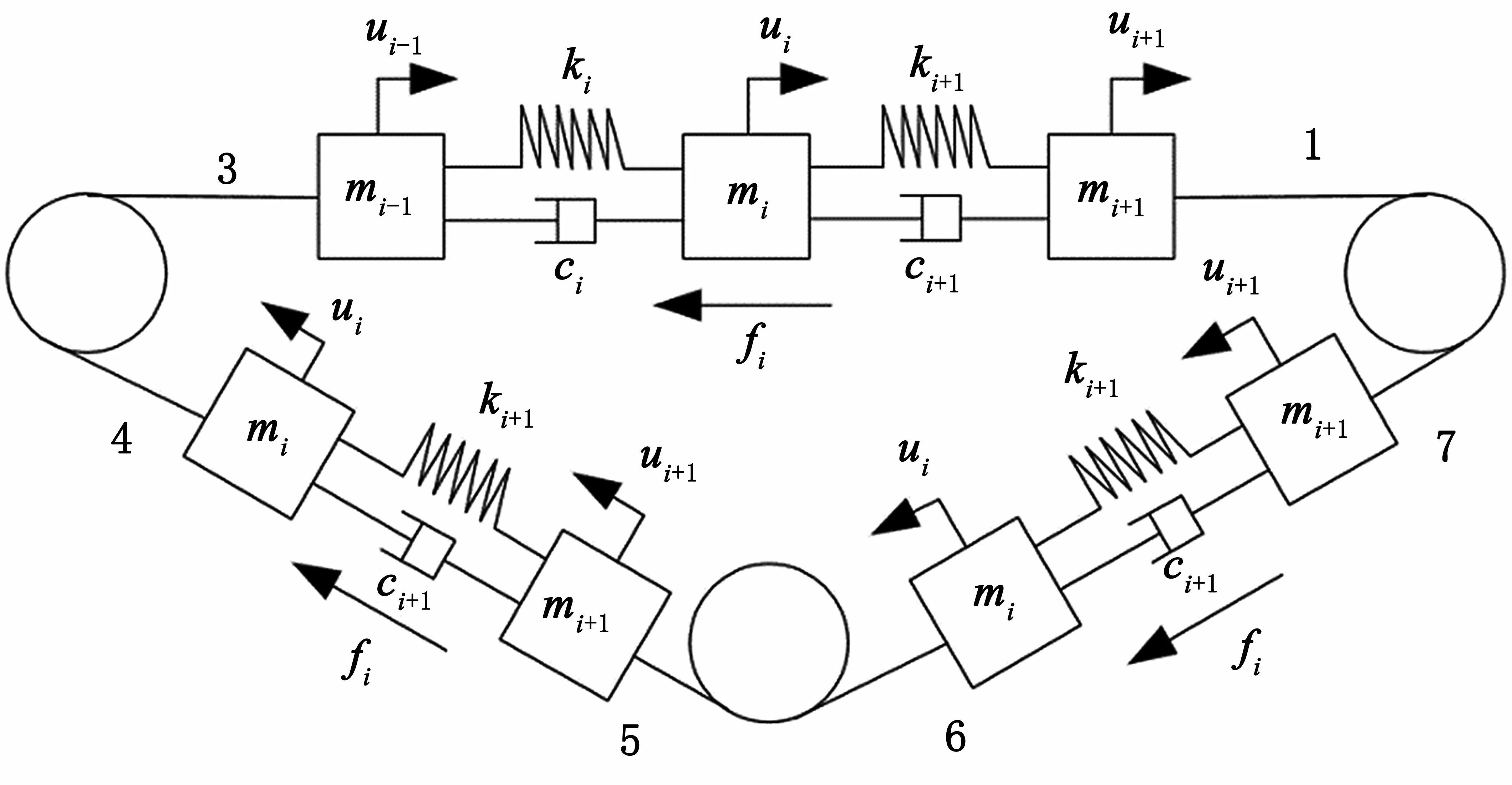
图3 传送带力学模型
皮带传送动力学方程为
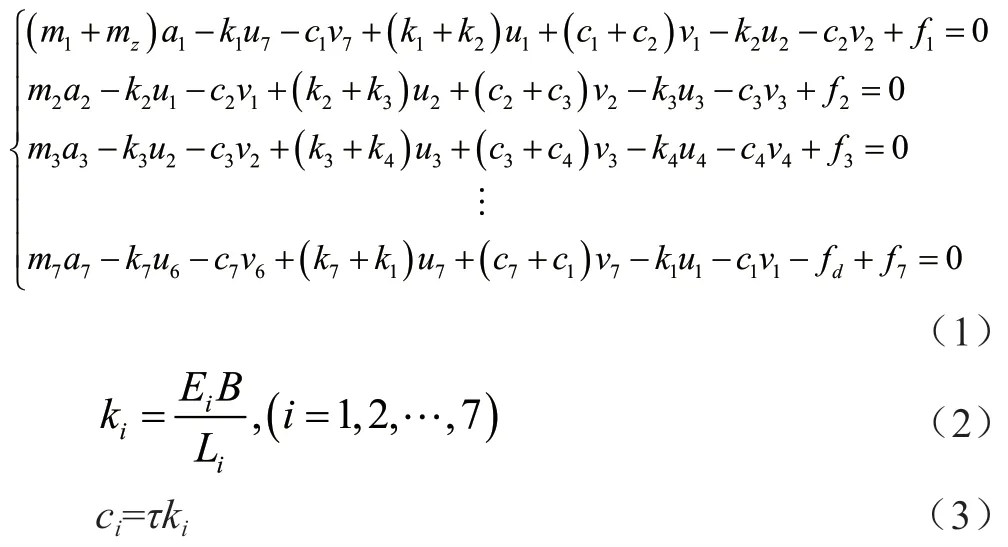
式中:ci、τ分别为各单元的等效阻尼系数、流变常数;ki、Ei、B、Li、fd分别为各单元的等效刚度、等效弹性模量、带宽、皮带划分长度、运行阻力、驱动扭矩;ui、vi、ai分别为各单元的位移、速度、加速度[8]。考虑运转过程中固定板与六角滑轮的摩擦影响,需计算克服摩擦的驱动扭矩fb。
驱动扭矩fb=μmagr,其中μ为摩擦因素,ma为六角轮的负载质量,r为驱动轮半径,g为重力加速度。因此,玻璃传送机的总力矩f=fb+fd。
1.3 关键部件的柔性化处理
将整机模型导入ADAMS,结合传送机结构特点和运行过程中的振动,需要考虑固定板的变形。在整机刚体动力学模型中将固定板柔性化处理,如图4所示,并输出为.mnf格式[9]。

图4 固定板柔性化
将柔性化部件替换为整机模型中的刚性部件,完成替换后如图5所示。设置重力加速度为9.8 m·s-2, 接触面的刚度系数为3×108N·m-1,阻尼系数为 1 000 N·m-1·s,动摩擦系数为0.1,静摩擦系数为0.3,并添加装配约束如表1所示。

图5 玻璃传送机刚柔耦合模型

表1 约束施加
2 传送机动态性能仿真结果与分析
2.1 固定板变形受力分析
利用ADAMS有限元软件对玻璃传送机运动过程进行仿真计算,仿真时间为5 s,分析柔性化处理的固定板的变形剧烈程度。它的质心点角动量曲线,如图6所示。
由图6可知,在玻璃传送机运行的第1 s,固定板的质心有了一个很高的波动,最大角动量为0.562 N·mm2。 但是,在其变形后,质心的角动量未发生较大波动,表明固定板在高速运转过程中未有太大的变形趋势。
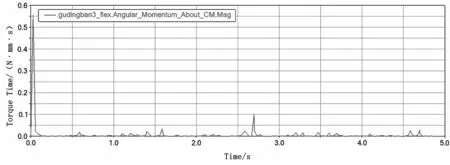
图6 固定板角动量曲线图
由图7可知,玻璃传送机在运转过程中,质心点位置在很短时间内受到了较大的变形挤压,并在很短时间内衰落稳定在15 N。传送机在启动时有一个较大的启动加速度,但在皮带转动速度趋向于匀速运动时,玻璃传送机固定板的变形挤压同时趋向于稳定。

图7 固定板受力曲线图
2.2 六角轮角速度与角加速度分析
由图8可知,在给带轮添加初始驱动后,六角轮在六角轴的带动下随着带轮一起转动,其加速度在短暂的波动后到达峰值点并迅速降低。后续转动中,角加速度虽然有波动,但趋近于稳定。由图9可知,六角线轮的角速度在启动时快速上升,但又在0.3 S时降为零,而后又迅速升高,并在2.5 s后稳定。由此可以得出结论,固定板的振动变形对六角轮的转动有影响,但是不会对玻璃传送机的运转造成太大影响。
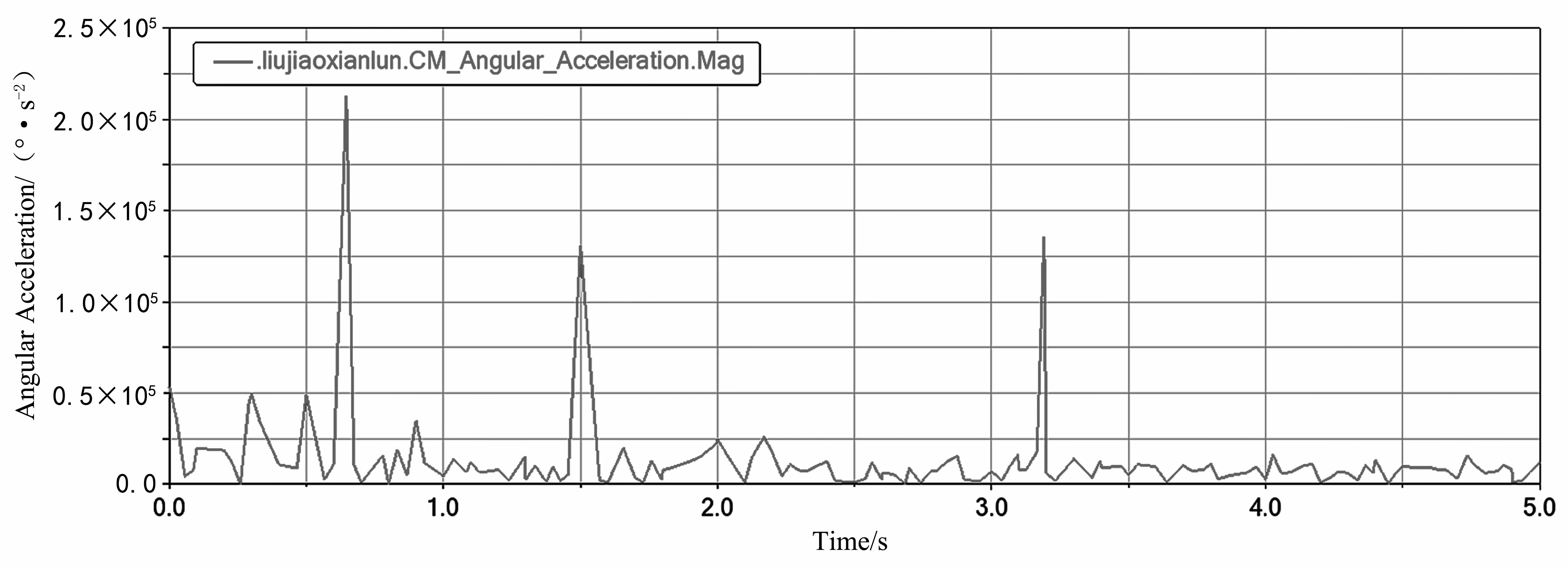
图8 六角轮角加速度曲线
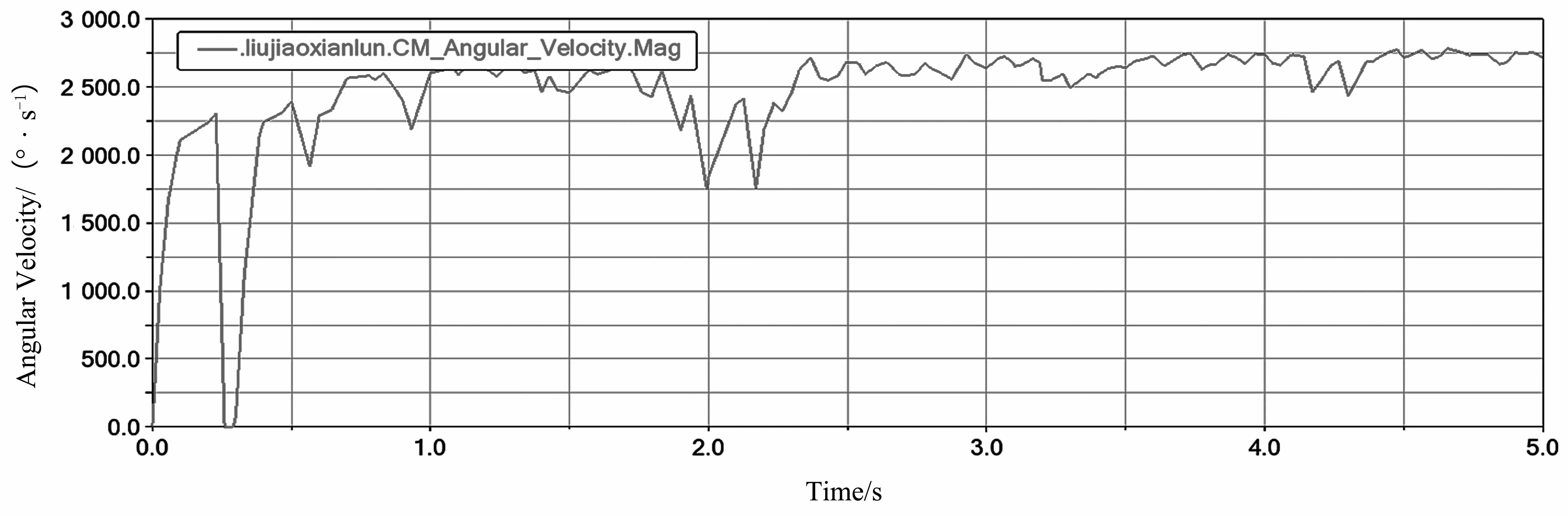
图9 六角线轮角速度曲线
由图10和图11可知,随着驱动扭矩的增加,六角轮与固定板之间的振动产生的碰撞不断延迟。驱动扭矩为50 N·m,初次碰撞时间为0.35 S。驱动扭矩为70 N·m时,初次碰撞时间为0.42 S,首次碰撞时间延长了0.07 S。驱动扭矩为50 N·m时,前2 S因振动产生的碰撞次数较少;在2~4 S时,碰撞次数较为频繁;4 S后,趋向于平稳。当驱动扭矩为70 N·m时,在0~1 S和2~3 S时,碰撞次数较多,碰撞频繁;4 S之后,碰撞次数减少,且增大驱动时碰撞力最大幅值并未改变。
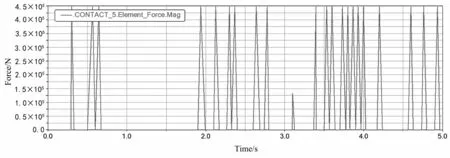
图10 扭矩为50 N·m刚度系数3×107 N·m-1碰撞力曲线
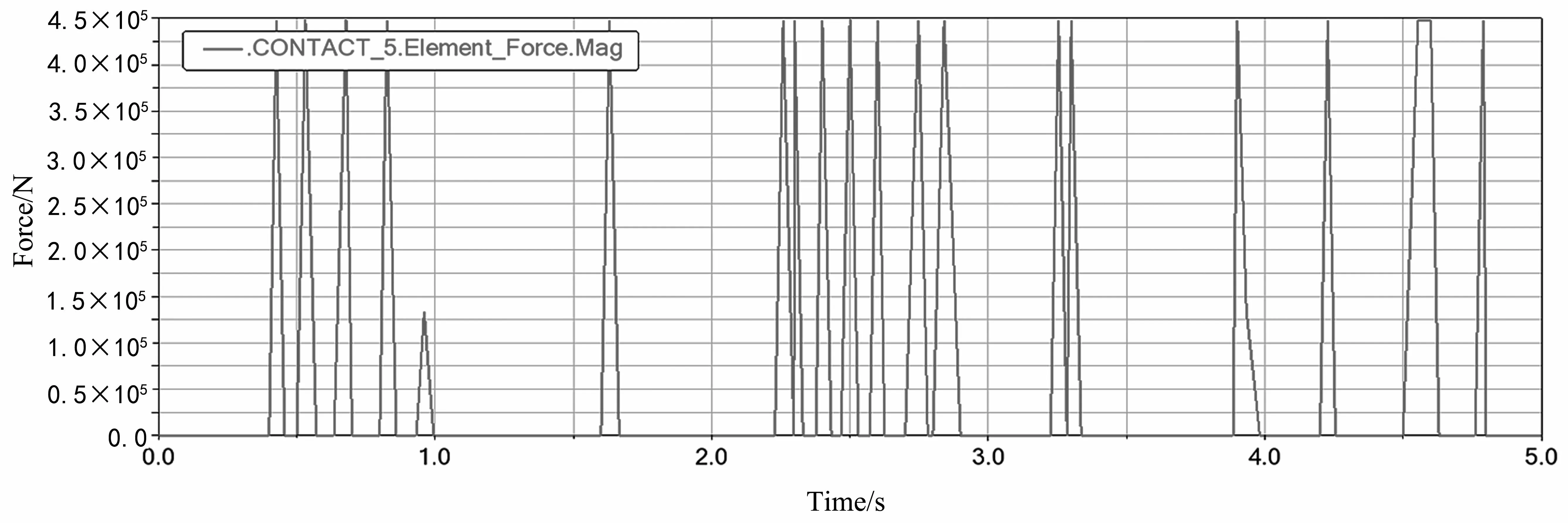
图11 扭矩为70 N·m,刚度系数3×107 N·m-1碰撞力曲线
由图12可知,当驱动扭矩相同时,刚度系数越大,产生的碰撞力越大。前3 s的碰撞次数较少,碰撞较为分散;3 s之后,碰撞较为频繁。可见,扭矩的增大不会影响碰撞力大小,但会延长初次碰撞的时间,并会造成碰撞集中。相同条件下,虽然刚度系数的增加会强化因振动产生的碰撞力,但会减少碰撞次数且使其更为分散。
3 结语
在传送传送过程中,玻璃传送机的柔性部件虽然会因振动产生变形,但是会在短暂的波动后稳定,不会对传送过程造成太大影响,验证了其结构的合理性。此外,玻璃传送机的输出扭矩越大,初次碰撞时间越延后,碰撞次数越集中,传送稳定时间越提前;玻璃传送机接触面的刚度系数越大,产生的碰撞力越大,碰撞次数越分散。

