基于改进粒子群算法的红外灯阵自动优化设计

张筱娴，林士峰，张 旭，林宝军,2,3,4，蒋桂忠

（1. 中国科学院 微小卫星创新研究院； 2. 上海科技大学 信息学院：上海 201210；3. 中国科学院 空天信息创新研究院； 4. 中国科学院大学 计算机科学与技术学院：北京 100094）

0 引言

红外灯是常用的航天器外热流模拟装置，因其使用灵活，对航天器表面遮挡较小，且能够重复使用，被广泛应用于航天器真空热试验中。对于红外灯阵的优化设计，国外航天机构的相关研究工作较早就有报道：1986 年，Sanger研究了一种新型的红外灯，并计算得到其较精确的热流分布；1994 年，Turner 等采用蒙特卡罗方法计算红外灯的热流分布，并以此作为红外灯阵优化的基础；2004 年，Ziemke使用有限元法分析了红外灯的热流分布并优化灯阵设计。

国内这方面的研究起步较晚：2010 年之前，主要采用试验方法测试红外灯阵热流的不均匀度；2010 年，张坤等对带抛物面型反射器的红外灯泡进行了辐射仿真分析；2010 年—2011 年，北京卫星环境工程研究所对管状红外灯进行了单灯热流仿真，并使用遗传算法优化了灯阵设计，此后又提出曲面红外灯阵热流仿真方法，结合遗传算法和复合形算法进行灯阵优化设计，并在单灯热流仿真的基础上分析影响灯阵热流均匀度的参数，以指导灯阵的优化设计；2012 年之后，国内对提高红外灯阵热流均匀度的研究较少，鲜有的研究仅基于实验和数据拟合，误差较大，通用性也有限。

单纯使用数学计算方法对已有的红外灯阵进行优化设计，需要输入初始的阵列参数，且遗传算法虽然擅长找到全局最优解，但收敛较慢、运行时间长，在实际工程应用上不具优势。目前国内各大科研院所在进行航天器热试验时，仍以传统的灯阵设计手段为主，即先根据经验设计灯阵的间距和高度，再根据测得的热流均匀度来调整灯阵布局，不仅费时费力，且热流均匀度较差，影响真空热试验结果的准确性，进而影响航天器的热设计效率。

为能快速地针对不同尺寸的卫星散热面设计出适用的灯阵布局，本文提出一种基于改进粒子群算法的红外灯阵自动优化设计方法，结合工程经验对优化参数进行约束，以求在提高收敛速度的同时能较准确地获得全局最优解，更加适用于红外灯阵优化设计的工程应用。

红外灯阵自动优化设计的基础是较为准确地计算掌握红外灯阵的热流分布，由于各类商业热分析软件难以分析灯管对灯丝不同波段能量的折射、反射等情况，所以当前设计中普遍采用蒙特卡罗法计算红外灯的辐射热流。蒙特卡罗法通过追踪光线轨迹来获得热流分布，能够有效解决复杂的热流计算问题，但获得精确结果的代价是较长的计算时间。为了简化计算，通常先计算不同安装高度的单灯热流分布，获得红外单灯热流分布数据库，然后忽略各个红外灯之间的互相影响，通过坐标变换、叠加网格热流来计算红外灯阵的热流分布。

以国内常用的飞利浦13169X/98 型号红外灯为例，灯丝为钨丝，发射率接近1，绕制成单螺旋圆柱体样式，可等效为一个圆柱体。由于红外灯的灯管是封闭体，灯丝发出的能量一部分被灯管吸收，一部分由灯管透射出去，其余经反射等过程最终被灯管吸收或透射。

灯管的材质为石英玻璃，对波长0.2～4.0 μm的粒子只透射或反射，对此波段外的粒子只吸收或反射，即有3.8 μm 宽的透射谱带。代表能量的粒子在灯管上的反射/透射/吸收与粒子的波长和入射方向均有关。光谱反射率的计算方法可表示为

1 红外灯阵热流分布计算

1.1 单灯热流分布

式(1)和式(2)中：()和()分别为反射率的法向分量和平行分量；为粒子的入射角；和分别为石英玻璃的折射率和吸收系数，可查表得到。

灯管吸收部分灯丝的能量后温度升高，成为不可忽略的二次辐射源，可视其为灰体，发射率取0.94。叠加由灯丝和灯管发出的辐射热流，可以计算出被照平面上的热流分布，求解流程如图1 所示。

图1 单灯热流分布求解流程Fig. 1 Solution process for calculating heat flux distributions for a single lamp

根据工程经验，红外灯的安装高度通常在0.3～0.6 m 之间，故本文计算此安装高度区间内的红外单灯的热流分布，计算间隔为0.1 m，和方向分别垂直和平行于红外灯的轴线方向，为灯的安装高度，图2 给出部分安装高度的单灯热流分布。

图2 不同安装高度的单灯热流分布Fig. 2 Heat flux distributions for a single lamp at different installation heights

图3 为某卫星热试验用红外灯阵。灯阵平行于卫星散热面排布，同一平面的红外灯可安装在相同或不同高度，为了提高热流均匀性，一般在灯阵的周围加设反光板。计算灯阵热流时需考虑多个红外灯直射热流与四周反光板反射热流的叠加。

图3 某卫星热试验用红外灯阵Fig. 3 The infrared lamp array for a satellite’s thermal test

如图4 所示，被照面上的每一个网格点，不仅接收来自每只红外灯的直接辐射热流，还接收来自每块反射板对每只灯的反射热流。因此，被照面上任一网格点的热流计算式为

1.2 灯阵热流分布

式中：为网格点的总热流；和分别为红外灯的直接热流和反射热流；为红外灯的总数量；为反光板的总数量。为简化示意，图4 只展示了1 块反光板的反射热流和4 只红外灯的直接热流，其中反光板对红外灯的反射可视为镜面反射。

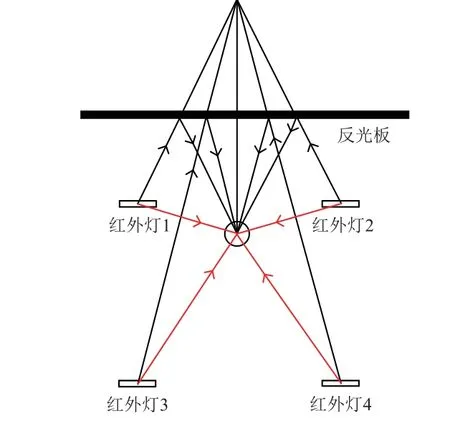
图4 被照面热流示意Fig. 4 The heat flux on the illuminated surface

工程上通常使用热流不均匀度来衡量被照面红外灯阵的热流分布均匀性，其计算公式为

其中，和分别为红外灯阵在被照面的最大和最小热流密度。

1.3 计算结果验证

1）单灯热流计算验证

计算输入功率为71 W、红外灯高度为0.3 m 条件下的单灯热流分布，计算结果由灯丝热流和灯管热流叠加而得。由于灯管的热流计算不涉及石英玻璃的光谱特性，使用商业软件同样能够得到较为精确的结果，所以将本文程序计算得到的灯管辐射热流与商业软件仿真得到的结果进行比对验证，如图5 所示，可以看出两者一致性良好，证明本文计算方法基本无误。

图5 单灯灯管热流的本文计算结果与商业软件仿真结果对比Fig. 5 Comparison of the heat flux for a single lamp tube between the calculation results obtained with this paper’s method and the simulation results obtained with commercial software

以本文程序计算方法，采用文献[2]中的红外灯参数，计算输入功率1032 W、安装高度0.152 4 m条件下的单灯热流分布；并与文献[2]的计算和实测结果进行比对验证，如图6 所示，可以看出，本文方法与文献[2]的数据在中心区域一致性良好，证明本文计算方法基本无误。

图6 单灯热流的本文计算结果与文献数据对比Fig. 6 Comparison of the heat flux for a single lamp between the calculation results obtained with this paper’s method and the reference data

2）灯阵计算验证

为了验证本文灯阵热流分布计算的正确性，借用文献[7]中的灯阵尺寸进行计算，并与文献[7]的灯阵热流数据进行比对验证。灯阵为7 行×6 列均匀分布，每只灯安装高度均为0.45 m，本文计算所得灯阵热流分布如图7 所示，不均匀度为23.68%，与文献[7]中的24.61%高度符合，且数值范围基本一致，证明了本文采用简化方法计算灯阵热流分布是可行的。

图7 本文的红外灯阵热流分布计算结果Fig. 7 Calculated heat flux for lamp array on the work-plane

2 红外灯阵自动优化设计

红外灯阵的优化是个多参数优化问题，参数均连续变化且为实数，本文针对此特点引入粒子群算法进行优化计算。相比于遗传算法，粒子群算法具有记忆性，在搜索过程中仅跟随当前最优解，计算不需要编码，也没有交叉和变异操作，只通过内部速度进行更新，因此原理更简单、参数更少，多数情况下收敛速度更快，适用于实数问题求解。

2.1 粒子群算法

粒子群算法，又称粒子群优化算法（PSO），是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。假设搜索空间是维，群体中有个粒子，则群体中第个粒子在维搜索空间的位置为X，X=(x,x,…,x)，=1, 2,…,。X经过的最佳位置为=(P, P,…,P)，=1, 2,…,。粒子的每个位置代表要求的一个潜在解，代入目标函数即可得到它的适应度值，用于评价粒子的“优”“劣”。整个群体的最佳位置为=(P,P,…,P)，是最优粒子位置的索引。粒子飞行速度与位置的关系可表示为

从式(5)和式(6)可以看出，粒子群算法是一种非常简便的优化算法，单次计算需要调整的参数个数少，各粒子“自我学习”的同时“相互学习”，计算速度非常快。

2.2 改进的粒子群算法

1）优化参数的确定

红外灯阵的热流分布其实是每只灯辐射热流在空间上的叠加结果，因此，实质上影响红外灯阵热流分布均匀度的是各灯在、方向的间距以及向的高度。传统方法直接使用各红外灯的位置而不是间距作为优化参数，算法每次更新迭代时，一旦灯的位置改变，灯阵间距参数也会发生改变，而且这种改变的影响因素有2 个，因此产生了很多计算冗余。

本文直接使用两灯间距作为优化参数，能够减少这种计算冗余，加速优化。相邻两只灯向的间距为（、、…），向的间距为（、、…），每只灯距被照面的高度为（、、…）。为简化计算，将灯阵分为4 个象限，不同象限的灯阵位置对轴、轴对称，以减少待优化的参数总数。

选取右上角1/4 灯阵的高度参数为优化参数。当灯阵的行数或列数为偶数时，选取的1/4 灯阵的行数为/2、列数为/2；当灯阵的行数或列数为奇数时，选取的1/4 灯阵的行数为(+1)/2、列数为(+1)/2。以4 行×4 列的灯阵和3 行×3 列的灯阵为例，如图8 和图9 所示。

图8 4 行×4 列灯阵的1/4 灯阵选取示意Fig. 8 A quarter selection of the 4×4 lamp array

图9 3 行×3 列灯阵的1/4 灯阵选取示意Fig. 9 A quarter selection of the 3×3 lamp array

对于灯阵的间距参数，采取同样的方法选取右上角1/4 的灯阵间距参数作为优化参数。当灯阵的行数为、列数为时，有-1 个行间距参数、-1 个列间距参数，因此，当灯阵的行数或列数为偶数时，则选取的1/4 灯阵间距参数矩阵的行数为/2、列数为/2；当灯阵的行数或列数为奇数时，则选取的1/4 灯阵间距参数矩阵的行数为(-1)/2、列数为(-1)/2。

2）优化参数间的约束

优化计算时，根据工程经验，遵从灯阵间距由中心至外围逐渐减小、灯阵安装高度由中心至外围逐渐降低的原则约束优化参数，以加快收敛速度。以6 行×6 列的灯阵为例，选取的间距参数矩阵为3×3，选取的高度参数矩阵为3×3，向的间距由左至右分别为Δ、Δ、Δ，向的间距由下至上分别为Δ、Δ、Δ，高度参数矩阵如图10 所示。

图10 6 行×6 列灯阵优化计算时选取的高度参数矩阵Fig. 10 Altitude parameter matrix selected for the optimization of 6×6 lamp array

则有

由于随机迭代过程中各参数之间存在约束关系，能够很大程度上减少计算量，提高迭代速度，且能减弱陷入局部最优的倾向。

2.3 方法步骤

为缩短计算收敛时间，做以下处理：

1）由工程经验，、向间距一般在0.3～0.5 m之间，高度一般在0.3～0.6 m 之间；

2）每行灯的坐标相同、每列灯的坐标相同；

3）、向的优化步长为5 mm，向的优化步长为10 mm；

4）对于迭代过程中出现越界的参数，使用图11所示的方式处理。

图11 优化参数的越界处理Fig. 11 Handling of overrange parameters in the optimization process

针对典型的矩形航天器散热面，红外灯阵自动优化设计的基本思路为：

1）使用蒙特卡罗法计算高度在0.3～0.6 m之间、固定输入电流下的单灯辐射热流分布，计算步长为0.1 m，得到红外灯单灯热流分布数据库。

2）基于工程经验设定灯阵向、向的初始间距和向的初始高度，根据散热面的长与宽计算灯阵的初始行数与列数，并计算灯阵的初始热流不均匀度。

3）划分象限，选取待优化的参数。

4）采用粒子群算法对行×列红外灯阵进行优化，目标函数为灯阵的热流不均匀度(Δ,…,Δ,…,,…)。

5）在设定的最大循环次数之内，当小于目标值（通常为10%）时停止迭代；当循环次数超出且仍未达到目标值时，将灯阵的行数或列数增加1，重复步骤2）～5），直至小于目标值。

6）输出红外灯阵设计参数。

3 结果分析

3.1 改进效果

为了显示本文的改进策略对红外灯阵优化速度的促进，以2.1 m×2.0 m 的卫星散热面为例，指定灯阵为7 行×6 列，分别使用遗传算法、粒子群算法和改进的粒子群算法进行灯阵的优化设计，图12为各算法的计算速度对比。

图12 各算法的计算速度对比Fig. 12 Comparison of calculation speed among different methods

从图12 中可以看出：使用遗传算法优化灯阵，热流不均匀度降至10%以下耗时75.8 min，计算305.4 min 后的最终热流不均匀度为6.75%；使用粒子群算法进行优化，热流不均匀度降至10%以下耗时56 min，比遗传算法用时缩减26.1%，但计算100 min 后的最终热流不均匀度稳定在9.88%，无法继续下降；使用改进的粒子群算法进行优化，计算仅8 min 后热流不均匀度即降至9.25%，比遗传算法用时缩减89.4%，且计算55 min 后的最终热流不均匀度为7.52%。可见与遗传算法相比，改进的粒子群算法的优化总时长可缩减82%，虽然最终优化结果相对差了0.77%，但加速效果显著，更贴合实际工程应用的要求。

为更全面评估改进的粒子群算法的优势，将其优化结果与传统粒子群算法的优化结果进行对比，并将二者坐标范围设为一致以便于比较，如图13所示。图中可明显看出算法改进后的优化灯阵热流分布更加均匀，而算法改进前优化结果中灯阵的边缘热流密度往往较大。

图13 粒子群算法改进前后的计算结果对比Fig. 13 Comparison of calculation results before and after improvement of PSO

3.2 矩形散热面红外灯阵优化实例

对2.1 m×2.0 m 的矩形散热面进行红外灯阵自动优化设计，将热流不均匀度的目标值设为8%。自动计算的初始灯阵为6 行×6 列，迭代计算150 次后的热流不均匀度为12.05%；因其未达到目标值，程序自动将灯阵行数增加1 行，再对7 行×6 列的红外灯阵进行优化，热流不均匀度为7.52%时计算完成。同理，对1 m×1 m 的散热面进行灯阵优化设计，设计所得的灯阵为4 行×4 列，热流不均匀度为6.8%。上述灯阵的位置参数和热流分布如图14～图17 所示。

图14 7 行×6 列灯阵位置参数Fig. 14 Optimized result of position parameters of 7×6 lamp array

图15 7 行×6 列灯阵热流分布Fig. 15 Optimized result of heat flux distributions for 7×6 lamp array

图17 4 行×4 列灯阵热流分布Fig. 17 Optimized result of heat flux distributions for 4×4 lamp array

4 结束语

本文基于粒子群算法建立了红外灯阵自动优化设计的方法，不需要预设灯阵的初始参数，即可自动为不同尺寸的矩形散热面设计出符合热流均匀度要求的红外灯阵，直接供工程使用。为提高优化设计效率，对粒子群算法做了针对性的改进：使用两灯间距作为优化参数，减少计算冗余；遵从灯阵间距由中心至外围逐渐减小、灯阵安装高度由中心至外围逐渐降低的原则约束优化参数，以加快收敛速度，减弱陷入局部最优的倾向。

改进的粒子群算法与传统遗传算法的计算对比结果证明本文改进策略能有效加快优化速度，且方法简便，可降低采用红外灯阵进行热真空试验的时间成本，对卫星批量化生产具有一定实用价值。