波浪滑翔机能量管理策略设计与仿真

梁 鑫， 王 鹏， 刘然然， 田新亮， 彭 涛

(上海交通大学 海洋工程国家重点实验室， 上海 200240)

0 引 言

海洋观测是研究海洋、开发海洋、利用海洋的基础。现有海洋观测装备如浮标、科考船等往往受限于海洋观测大尺度、长时序的特点，因此亟须研制能进行大范围、长航时海上观测的新型装备。波浪滑翔机是一种完全由自然能源驱动的无人航行器，能够将波浪能转化为前进动能，并且利用太阳能为船上各电气设备供电，从而实现无限航程的续航，为海洋观测技术带来新突破。然而，由于完全由自然能源驱动，波浪滑翔机的能量来源具有间歇性和不确定性，同时其用于储能的电池容量有限，并配有多种负载，这些因素给波浪滑翔机系统的长期稳定高效运行带来了极大的挑战。因此，有必要设计一种能量管理策略对系统内各电气设备进行能量调度，以提高波浪滑翔机长期运行时的稳定性和能量利用效率。

能量管理包含对发电端、储能端和负载端等3方面的管理[1]。现有文献关于船舶能量管理策略的研究大多集中于对混合动力船舶的发电端和储能端管理而忽视负载端管理，且相关能量管理目标一般是以考虑经济成本和环境污染为主的指标[2-3]。ANVARI-MOGHADDAM等[4]提出一种基于混合整数非线性规划的能量管理策略以实现对柴油发电机和储能设备的最优管理，从而使船舶整体运营成本最小。KANELLOS等[5]提出一种同时考虑发电端和负载端的能量管理策略以在满足到港时间和温室气体排放限制的条件下进一步降低船舶运营成本。FANG等[6]同时考虑燃料消耗、温室气体排放和电池生命周期等3个目标，得出对发电机、储能系统和螺旋桨的最优调度。上述研究或者不考虑负载，或者仅考虑螺旋桨为唯一可调度负载。但是如前所述，除螺旋桨外，波浪滑翔机还搭载许多其他类型的负载以执行不同任务，其同样应被视为可调度负载，成为能量管理策略的管理对象，因此之前的船舶能量管理策略均不适用于波浪滑翔机。

本文提出一种适用于波浪滑翔机的能量管理策略。首先，利用混合整数非线性规划模型对不同类型电气设备的运行约束和相关目标函数进行数学建模，构建多目标优化问题。其次，基于不同任务模式，利用ε-约束法和线性加权法将多目标优化问题转化为等效单目标优化问题进行求解。最后，通过仿真试验验证能量管理策略的有效性，并对不同任务下的能量调度结果进行分析研究。

1 波浪滑翔机能量管理策略建模及求解

如图1所示，波浪滑翔机的能量系统由发电单元、储能单元和多个负载单元组成，每个能量单元都有相应的运行约束和目标函数。能量管理控制器根据用户提交数据及相关预测数据，可计算出对各单元的最优能量调度，并据此进行控制。因此，波浪滑翔机能量管理问题可抽象为多目标优化问题，其控制变量为各电气设备在未来一段时间内的功率状态，优化目标为与不同设备相关的不同目标，约束条件为系统中的物理约束及用户自定义约束。对不同类型电气设备进行详细的数学建模，相关符号说明如下：T为当前调度周期，由T个连续且长度为Δt的子时段组成，索引为t，即t=1,2,…,T；z为二元变量，用来表示某功率状态的激活与否；P为输出功率，规定输出功率为正数时表示消耗电能、负数时表示产生电能。

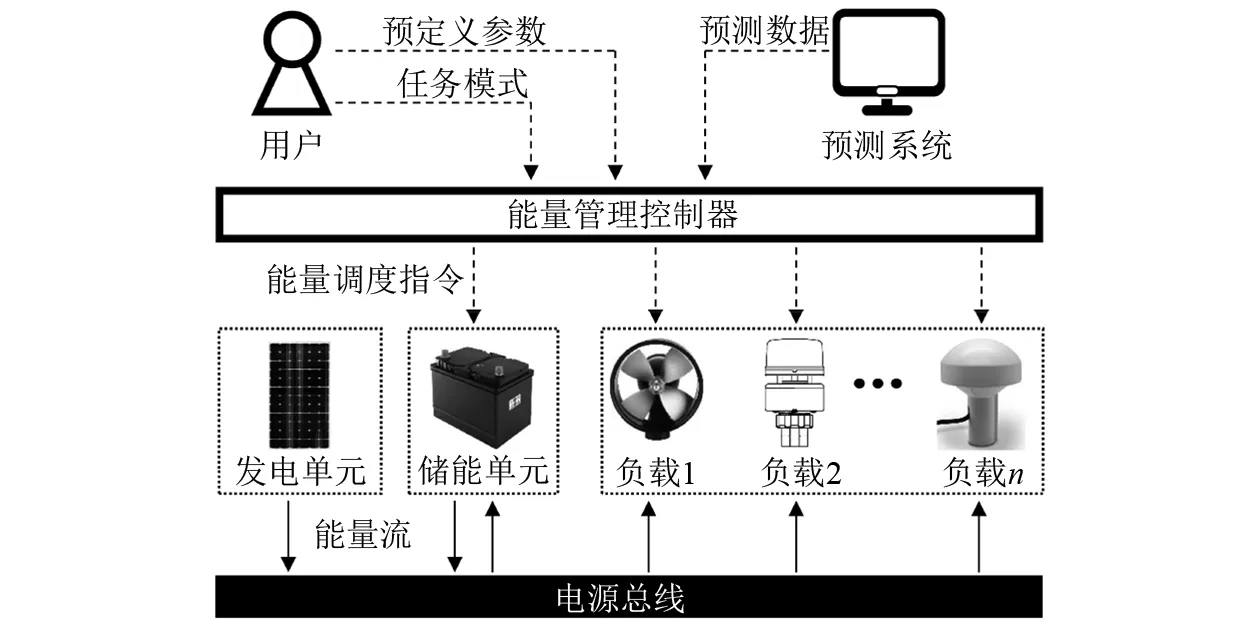
图1 能量管理系统示例

1.1 发电单元

太阳能板是波浪滑翔机唯一的发电单元，其发电功率记为PPV(t)，主要受环境条件影响，可由相关工具进行预测[7]，因此可视为已知参数。

1.2 储能单元

电池是常用储能单元，用来平衡发电量与负载耗电量间的差值，其输出功率Pbatt(t)和电池容量x(t)需维持在一定范围内：

-Pdch,max≤Pbatt(t)≤Pch,max,t∈T

(1)

xmin≤x(t)≤xmax,t∈T

(2)

式中：Pdch,max和Pch,max分别为最大放电功率和最大充电功率；Pbatt(t)为在第t子时段内电池的输出功率；xmin和xmax分别为最低电量和最高电量；x(t)为在第t子时段结束时的电池容量，其更新规则为

x(1)=xinit+Pbatt(1)Δt

(3)

x(t)=x(t-1)+Pbatt(t)Δt,t=2,3,…,T

(4)

式中：xinit为电池初始电量。波浪滑翔机应用于海上长期作业场景，电池在当前调度周期T终止时刻的电量应维持在较高水平以便其能继续工作，因此将x(T)定义为与电池相关的目标函数。

1.3 负载单元

将波浪滑翔机上的负载分为4类，即基础负载、螺旋桨、恒功率负载和可调功率负载，其中后3类负载为可调度负载。

1.3.1 基础负载

基础负载，如定位模块、电罗经等，用于保证波浪滑翔机的基本航行能力，需时刻开启，因此其工作功率PBL(t)为已知常数。

1.3.2 螺旋桨

螺旋桨用来在环境能量不足时或者紧急状态下作为辅助推进装置。假定螺旋桨能够以np挡功率运行，记为gi,prop，对应用np个二元变量zon,i,prop(t)来表示螺旋桨在第t时段功率gi,prop是否处于激活状态，并用zoff,prop(t)描述螺旋桨关闭状态，用Pprop(t)表示螺旋桨输出功率，可得到如下约束：

(5)

(6)

式(5)表示螺旋桨同一时刻只能处于一种工作状态。式(6)给出螺旋桨工作功率计算式。假定总速度v由环境引起的速度vei和螺旋桨引起的速度vprop叠加而成：

v(t)=vei(t)+vprop(t),t∈T

(7)

式中：vei可由回归方法进行预测[8]，可视为已知参数；vprop(t)与Pprop(t)满足如下关系[9]：

Pprop(t)=c1vprop(t)3,t∈T

(8)

式中：c1为匹配系数。航行路程Ldist(t)表示在第t子时段结束时的航行路程，其更新规则如下：

Ldist(1)=Linit+v(1)Δt

(9)

Ldist(t)=Ldist(t-1)+v(t)Δt,t=2,3,…,T

(10)

式中：Linit为初始航行路程。通常，期望波浪滑翔机在给定时间内的航行路程越远越好，因此将当前周期T终止时刻的航行路程Ldist(T)定义为目标函数之一。此外，波浪滑翔机的航行精度同样值得关注。由于海洋环境极为复杂，定义一种近似精度指标。波浪滑翔机航速低、欠驱动的特性使其航行精度主要受海流影响[10]。增加航行速度是抵御海流影响的关键，因此将第t时段内的航行精度定义为该时段内的航行速度，即AL(t)=v(t)，进而可定义当前周期T内的整体航行精度AL：

AL=cAEE[AL(t)]-cAVD[AL(t)]

(11)

式中：E[AL(t)]和D[AL(t)]分别为周期T内精度的均值和方差；cAE和cAV为对应权重因子。式(11)表明，想要提高整体航行精度，既须提高每个子时段内的精度，又须缩小不同子时段间的精度差别。

1.3.3 恒功率负载

恒功率负载是只能以一挡功率gCPL运行的可调度负载。比如气象站、摄像机等传感器就属于此类负载。用二元变量zon,CPL(t)和zoff,CPL(t)和分别表示其开、关状态，用PCPL(t)表示恒功率负载输出功率，有如下约束：

zon,CPL(t)+zoff,CPL(t)=1,t∈T

(12)

PCPL(t)=zon,CPL(t)gCPL，t∈T

(13)

下面定义相关目标函数，记为恒功率负载满意度CPLS，与开启时长正相关，计算式为

(14)

式中：ctp,CPL(t)用来调节开启时段偏好：若设ctp,CPL(t)=γt-0，其中0<γ<1，此时负载开启时段靠前会产生更大满意度；相反，也可将参数设为ctp,CPL(t)=γT-t，表示更倾向于在靠后时段开启。

1.3.4 可调功率负载

可调功率负载是能以多挡功率运行的可调度负载，例如通信模块可通过改变通信频率来调节运行功率。假定可调功率负载能以nA挡功率运行，并且各挡功率gi,APL等间距分布。用二元变量zon,i,APL(t)和zoff,APL(t)表示对应的功率激活状态和开关状态，用PAPL(t)表示可调功率负载输出功率，则有如下约束：

(15)

(16)

下面定义相关目标函数，记为可调功率负载满意度，与功率等级和开启时长成正相关。为描述在相同能耗下，负载应优先以较高还是较低功率开启，定义可调功率负载以第i挡功率运行Δt时长所产生的满意度：

(17)

式中：λ和k为调节优先等级的参数：当0<λ<1时，在相同能耗下，负载优先以较低功率开启更长时间；当λ>1时，负载优先以较高功率运行。接下来定义当前周期T内的整体满意度APLS：

(18)

(19)

式中：APLS(t)为时段t内的满意度。

1.4 系统功率平衡约束

系统中唯一的耦合约束是功率平衡约束，计算式为

(20)

式中：m、n、o分别为不同基础负载、恒功率负载和可调功率负载的索引。由于该耦合约束的存在，能量管理问题并不能简化为分别优化各电气设备对应目标函数，而是要求各电气设备相互协调运行，从而使系统整体性能达到最优。

1.5 多目标优化问题求解

波浪滑翔机能量管理策略模型如下：

max[Ldist(T),AL,CPLS,n,APLS,o,x(t)]
s.t.(1)～(20)

(21)

该问题为多目标优化问题，不存在唯一最优解，因此基于不同任务模式，利用ε-约束法和线性加权法将其转化为单目标优化问题以进行求解。ε-约束法的核心思想是只保留最重要的目标，将其余目标限制在某一范围内形成新的约束条件；线性加权法的核心思想是将每个目标正则化后乘以相应的权重因子再求和得到新的目标函数[11]。

在各目标当中，电池终止电量的物理意义直观明确，且容易给出期望范围，因此可利用ε-约束法处理该目标，即给定电池终止电量的下界xT,lim，转化为新增约束条件x(T)≥xT,lim。该步骤决定了在当前周期T内可供可调度负载使用的能量，或者说在当前周期T内电能储存量与消耗量的比例，因此可基于不同任务模式确定xT,lim取值。当任务在T内完全结束时，无须对x(T)进行任何限制；当任务在T结束后继续进行时，则需要基于当前电量、净发电量估计和后续任务能耗估计等因素确定xT,lim取值。

当xT,lim确定后，需分别计算其余各目标最大可能取值，以进行正则化处理。最后需确定余下目标的权重因子ωi，该步骤决定了能量在各可调度负载间的分配。

不同xT,lim和权重因子ωi的组合决定了供可调度负载使用的能量总量及其分配方式，因此可基于不同任务模式确定各参数取值。经过上述步骤，原问题转化为如下单目标优化问题形式：

(22)

2 仿真和分析

2.1 参数设定

基于交鼠号波浪滑翔机各电气设备参数建立仿真能量系统[12]。各电气设备的类型和相关参数如表1所示。电池相关预定义参数为xmin=480 W·h，xmax=2 400 W·h。螺旋桨相关预定义参数为c1=336.4，cAE=0.3，cAV=1。初始电池电量设为1 200 W·h，初始航行路程设为0 m，T设为24 h，Δt设为1 h。图2为1 d内的PPV(t)和vei(t)变化曲线，数据分别来源于国家可再生能源实验室(NREL)[13]网站和海试数据[8]。利用开源求解器SCIP求解单目标混合整数非线性规划问题[14]。

表1 电气设备类型和参数

续表1 电气设备类型和参数

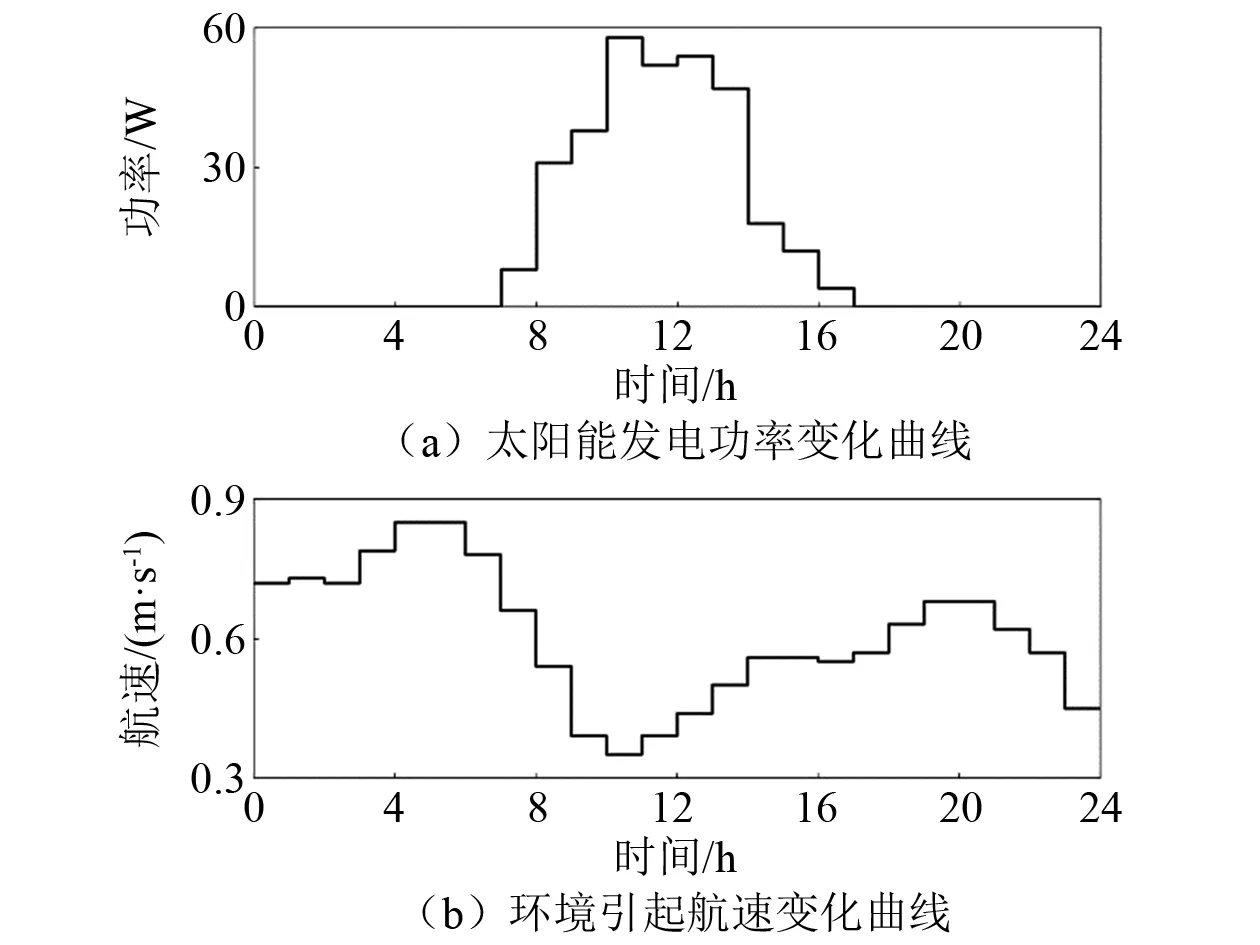
图2 环境参数变化曲线

2.2 能量管理系统模型验证

验证各可调度负载的目标函数和运行约束的有效性：针对螺旋桨，对比研究航行路程优先和航行精度优先对螺旋桨调度情况的影响；针对恒功率负载，验证开启时段偏好参数ctp,CPL(t)的作用；针对可调功率负载，研究参数λ的影响。具体的仿真试验参数设定如表2所示。

表2 仿真试验参数设定

图3为螺旋桨的仿真结果。如图3(a)所示，螺旋桨在2种情况下所消耗的总能量相等。在航行路程优先的情况下，螺旋桨采取以较小功率开启更长时间的调度策略，其原因在于，由式(8)可知，当螺旋桨功率增大时，螺旋桨所引起的航速增量减小。因此，在相同能耗下以较小功率开启的调度策略能获得更多的航速增量，从而使最终航行路程更大。在航行精度优先的情况下，如图3(b)所示，螺旋桨会在本身由环境引起的航速vei(t)较小的时段内以较大的功率开启，减小各子时段间的精度差异，从而使整体精度有所提高。图4展示开启时段偏好参数的影响：当ctp,CPL(t)=γt-0时，气象站会在早些时段开启；当ctp,CPL(t)=γT-t时，其会在周期T的末端开启。图5展示参数λ对通信模块调度策略的影响，在相同的能耗下：当λ<1时，通信模块优先以低功率挡位开启；当λ>1时，则优先以高功率挡位开启。由上述分析可知，所提出的能量管理策略能够在满足系统运行约束的前提下，实现对各设备的最优调度。

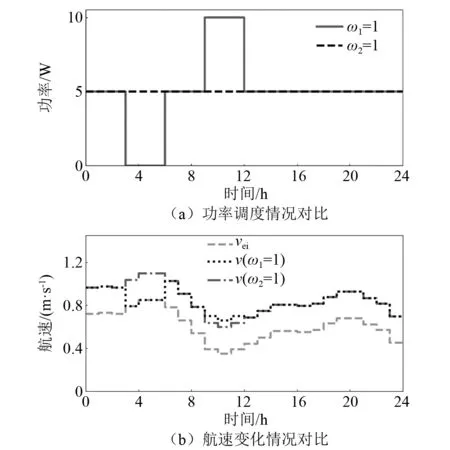
图3 螺旋桨仿真试验结果

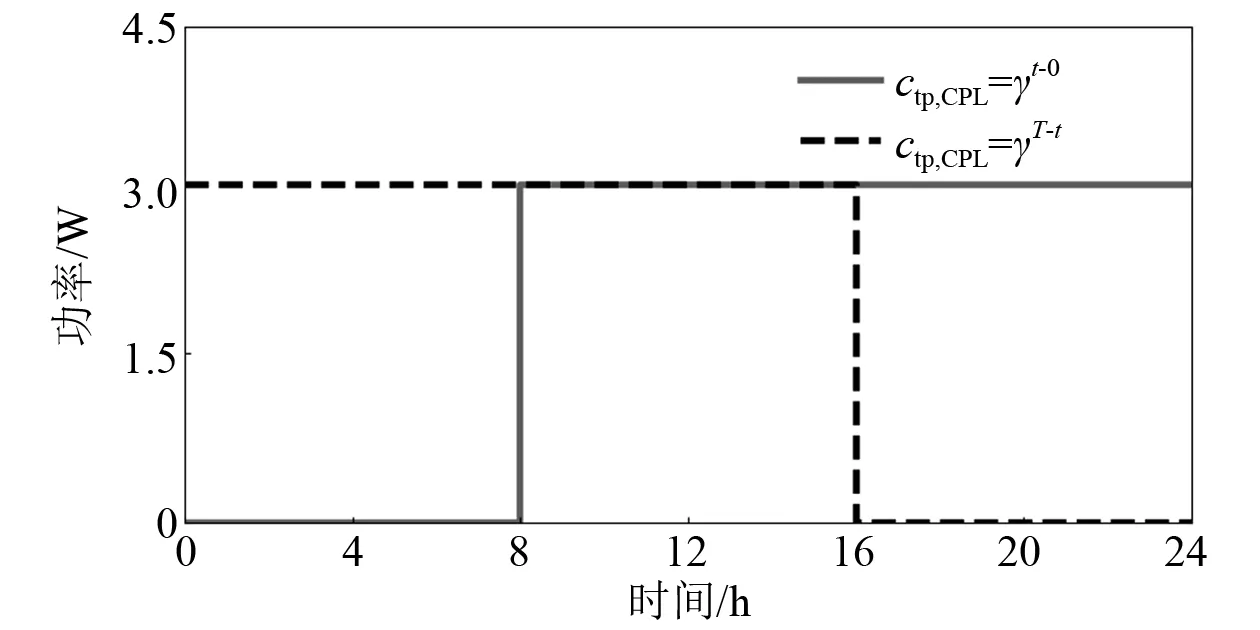
图4 开启时段偏好参数影响分析

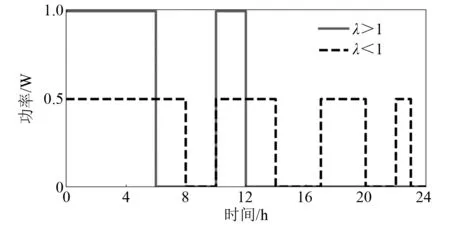
图5 λ参数影响分析

2.3 不同任务模式能量调度

表3列出一些典型任务及其对应的xT,lim和ωi取值。图6展示不同任务下的电池和可调度负载能量调度情况。

表3 典型任务模式及相关参数

如图6(a)所示，在性能测试模式下，为充分测试各设备，对xT,lim不进行限制，因此所有可调度负载均以最大功率运行。在图6(b)和图6(c)中，将xT,lim设为1 120 W·h，因此供可调度负载使用能量是相同的，但在不同负载间的分配方式不同。在定点和走航数据采集任务中，采集传感器气象站全天候保持开启，而螺旋桨调度策略因采集模式而异，在定点保持采集模式中，航行路程目标无意义，因此与螺旋桨相关的目标只需考虑航行精度，如图6(b)所示，此时螺旋桨选择在本身航速vei(t)更低的时段以较大功率开启以提高航行精度。在走航采集任务中，需同时考虑航行距离和精度，如图6(c)所示，螺旋桨会先以较低功率开启更长时段以获得更远航行路程，再将余下的能量来提升vei(t)更低时段的功率。如图6(d)所示，在快速航行任务模式中，要求滑翔机全速前进，同时汇报其实时位置，因此通信模块保持高频率运行，余下能量全部供螺旋桨加速航行。上述分析表明，通过选取不同的xT,lim和ωi，用户可以根据自身需求定义不同的任务模式，并且所提出的能量管理策略在不同任务模式下均能对各电气设备实现最优能量调度。

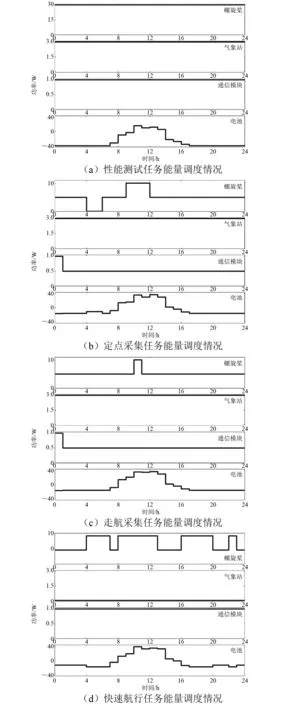
图6 不同任务模式能量调度情况对比

3 结 论

提出一种适用于波浪滑翔机的能量管理策略。

(1) 构建基于多目标优化方法的能量管理模型，能够灵活准确地对波浪滑翔机能量管理问题进行建模。

(2) 提出一种基于任务模式的能量管理多目标优化模型混合求解方法，该方法先利用ε-约束法进行能量在电池与负载间的初次分配，再利用线性加权法进行能量在不同负载间的再次分配。仿真结果表明该方法能够实现对各电气设备的最优调度，提高波浪滑翔机的长期运行稳定性和能量利用效率。