电场对中间神经元亚线性树突整合的调制作用
魏熙乐,樊亚琴,赵美佳,伊国胜,王 江
电场对中间神经元亚线性树突整合的调制作用
魏熙乐,樊亚琴,赵美佳,伊国胜,王 江
(天津大学电气自动化与信息工程学院,天津 300072)
中间神经元的树突形态大多呈现出空间对称性分布,使得电场在其胞体附近引起的膜电位极化作用微弱,因此大多数研究认为电场对中间神经元难以产生调制作用. 然而,电场在中间神经元末端的树突棘位置能够诱发较强的膜电压极化效应,远端的树突极化是否以及如何影响中间神经元的树突整合特性尚不十分清楚. 为此本文针对分散和集中空间分布的AMPA类型突触输入,研究了电场对中间神经元全局和局部亚线性树突整合特性的调制作用. 为了描述电场作用下树突对AMPA突触输入积分的潜在规律,首先建立了描述中间神经元输入-输出关系的简化电路模型,此模型具有多个被动树突分支且以不均匀细胞外膜电势表征电场诱发的极化效应;其次,基于奇异摄动理论分析了电场调节下的亚线性树突整合的动力学特性,推导出了可描述局部和全局树突整合的阈下输入-输出关系的渐近解析表达式. 理论分析结果表明,电场通过改变AMPA突触输入的驱动力调节中间神经元局部以及全局亚线性树突整合特性,调制效应依赖于电场对远端树突的极化程度. 相比于局部树突整合,电场对全局树突整合调制更敏感. 最后,利用电场作用下具有真实树突形态的海马CA1区中间神经元模型仿真验证了理论分析结果.
中间神经元;电场;极化;亚线性树突整合
在中枢神经系统中,兴奋性和抑制性神经元的共同激活被认为是各种大脑活动的基本原理[1].抑制性神经元主要为GABA能中间神经元,GABA能中间神经元通过释放GABA神经递质使得细胞膜超极化而抑制突触后神经元,进而控制和调节兴奋性神经元的活动[2],因此促进了信息的平稳流动以及维护了神经回路的稳态.兴奋性与抑制性(excitatory/inhibit-tory,E/I)神经元比例失衡导致癫痫、精神分裂症、阿尔茨海默病(Alzheimer’s disease,AD)和帕金森病等神经精神疾病[3-6].大量研究表明,GABA能中间神经元已经成为了治疗神经精神疾病的有效靶点.例如,Guzman等[7]对近年来GABA能信号系统作为治疗AD疾病的有效药物靶点的研究进行了概述;Xu等[8]发现调节GABA能系统是一种用于治疗精神分裂症的有效干预方法,并且讨论了将GABA能神经元作为认知缺陷的潜在治疗靶点和药物治疗的可行性.因此研究中间神经元有助于为治疗神经精神疾病提供理论指导.
经颅磁刺激[9-10](transcranial magnetic stimula-tion,TMS)是一种常用的有效的神经调控技术,利用短暂的电流通过电磁线圈所产生的感应电场调节神经系统,进而治疗脑疾病[11-12].锥体神经元不对称的树突形态使得电场在胞体处产生显著的极化作用,因此之前研究重点关注电场对锥体神经元的调制作用.Bikson等[13]在大鼠海马切片实验中,发现电场通过在近胞体处的极化调节了神经元的兴奋性,改变了神经元放电阈值和放电起始位置;Radman等[14]发现电场可以改变海马锥体神经元的放电时刻.电场在单神经元水平引起的放电时刻、放电阈值的变化会经过网络作用得到放大[15],从而调节海马区节律.对于树突形态对称的中间神经元而言,电场在胞体诱发的极化十分微弱[16],其胞体极化的重要性基本被忽略[17],因此大多数研究认为电场对中间神经元基本没有调制作用.Murphy等[18]发现,TMS产生的感应电场通过激活GABA能中间神经元而抑制皮层深层锥体神经元的树突活动,说明电场可以调节GABA能中间神经元的放电活动,进而影响神经回路的E/I平衡.但是在突触背景下,电场如何通过调制中间神经元树突整合而影响胞体响应尚不清楚.
树突整合被定义为突触后神经元将突触前信息转换为兴奋性突触后电势(excitatory postsynaptic potential,EPSP),并传输至胞体的过程,体现了对突触输入的整合,树突滤波以及胞体响应特性[19]. NMDA和AMPA作为两类重要的兴奋性突触,广泛分布在神经元的树突上[20].NMDA受体激活使得树突进行超线性整合[19],而AMPA受体激活使得树突进行亚线性整合[21]且有助于NMDA受体激活.非线性整合特性极大丰富了神经元计算功能,例如特征识别[22].突触电流动态特性在塑造树突亚线性整合中起着关键作用,对于相同的突触电导其驱动力为膜电势与突触反电势的差值,驱动力饱和导致树突亚线性计算[23].尽管加电场对中间神经元胞体的极化作用微弱,其在远端树突产生的较强极化作用可以改变突触电流的驱动力,因此本文提出假设:电场能够通过改变中间神经元远端树突膜电位,进而调节AMPA亚线性树突整合特性.
本文建立了一个能够描述多树突分支、多突触输入的中间神经元多间室电路模型,各个间室具有不同的胞外膜电势从而刻画了电场的空间极化效应.基于奇异摄动理论建立中间神经元动力学与AMPA类型树突整合之间的联系,推导出其输入-输出关系的渐近解析表达式.理论分析预测出电场的强度与极性在远端树突产生的不同极化对亚线性树突整合特性的调制作用,并对比了全局与局部突触分布对电场调制敏感性的影响.最后,利用电场作用下树突形态呈放射状对称的海马CA1区中间神经元模型进行仿真,验证理论分析结果.
1 模型与方法
1.1 中间神经元简化电路模型
1.1.1 单树突分支模型
不同于锥体神经元,大多数中间神经元的树突形态呈现空间对称性[17],因此不区分顶树突和基树突.本文以树突形态呈星状放射状对称的海马CA1区中间神经元模型[24]作为研究对象,对此进行建模,其三维树突形态如图1所示.由于中间神经元树突分支空间分布对称且大都直接连接至胞体,因此构建的模型树突形态对称,且各个树突分支的电缆模型结构相同,如图1(a)所示.该模型由胞体、远端树突和近端树突3部分构成,刻画了真实神经元远端树突接收突触信号并经近端树突传递至胞体的过程.
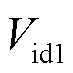

图1 单树突分支电缆及三间室电路模型
表1 模型被动参数取值

Tab.1 Passive parameter values of cable model
由单树突分支电缆模型得到其三间室模型,如图1(b)所示,该模型由远端树突刺激间室、近端树突间室和胞体间室构成,每个间室包含膜电容与漏电导,膜电容取值为1μF/cm2.两个相邻的间室通过轴向电导连接,根据电导计算公式,得到每个间室的漏电导以及连接相邻两个间室的轴向电导表达式为

神经元的每个间室都可以用一个具有独立膜电压的等效电路来表示,设置每个间室胞外膜不同的电势来体现电场作用下神经元不均匀的空间极化效应.图1(b)中,胞内与胞外膜电势的差值为跨膜电压,表达式为
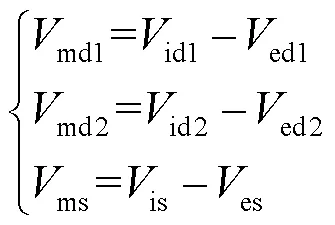
式中md1、md2、ms分别为3个间室的跨膜电压,由图1(b)列出每个间室跨膜电压的微分方程为
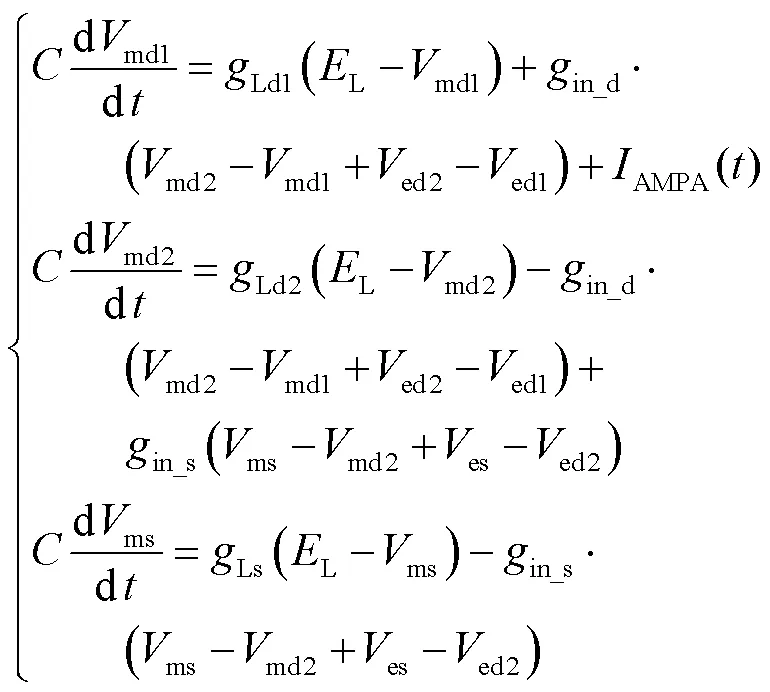

定义新的状态变量为

利用坐标变换得到单树突分支的等效3间室模型(见图1(c)).将方程(3)与(4)做差值,得到3个间室膜电位变化量的动力学方程为

利用坐标变换,得到电场作用下可刻画突触输入变化所引起的细胞膜电压变化量的状态方程,可用图1(c)的单树突分支等效3间室模型描述.
1.1.2 中间神经元的多树突分支模型



模型中多个树突分支可以看作并联关系,再通过轴向电导in_s与胞体间室连接,因此从个刺激分支流出的电流一部分流入胞体间室,一部分流入到非刺激树突分支,可表示为
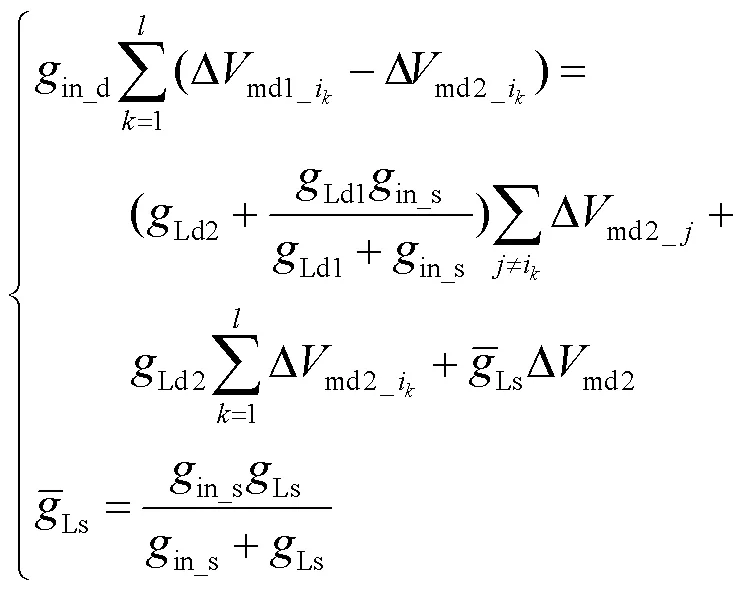
由此建立了一个描述多树突分支、多突触输入非对称分布的中间神经元电路模型,该电路模型描述了突触输入电流沿远端树突-近端树突-胞体路径传输到胞体的过程.
1.2 具有真实树突形态的中间神经元电场模型
NEURON仿真平台[25]是一个可以替代真实神经元进行虚拟实验的工具,其网址为https://neuron.yale.edu/neuron/.本文在NEURON软件中的ModelDB数据库中选取具有真实树突形态的海马CA1区中间神经元模型进行仿真实验(见图3),该模型由Saraga等[26]对一只小鼠的海马CA1区细胞进行重建得到,由胞体和呈放射状对称的三维树突形态构成,此模型下载网址为:https://senselab.med. yale.edu/ModelDB/ShowModel?model=28316.该模型的空间形态可以通过NEURON中的“点过程”机制实现,其树突直径变化范围从近端树突1.38μm到远端树突0.61μm;树突长度范围为70~330μm;轴向电阻为120Ω·cm;膜电容为1μF/cm2;胞体静息膜电位-65.21mV.由于阈下电场刺激下树突的主动离子通道活动较弱,本文中树突仅考虑了被动特性,重点研究电场对远端突触输入整合的调节作用,因此树突中不含主动离子通道.胞体中含有钠离子通道和钾离子通道,钠离子和钾离子电导分别为0.01S/cm2、0.0319S/cm2,AMPA电导为0.3nS.
基于NEURON软件中的“胞外机制”建立匀强电场,该建模方式常用在NEURON中模拟在电场刺激下神经元的空间极化效应以及其电活动[27].电场对神经元兴奋性的调制作用是通过其引起的空间极化效应实现的,如图3所示,靠近电场阳极的树突其膜电位降低而发生超极化,靠近电场阴极的树突其膜电位升高而发生去极化.本文对电场正负极性的定义如下:电场强度>0V/m时为正极性电场(见图3(a)),此时胞体去极化;电场强度<0V/m时为负极性电场,此时胞体超极化.图3(b)中,当电场强度从-20V/m以5V/m的步长增加至20V/m时,胞体最大极化大约为0.5mV,而锥体神经元胞体极化为5~10mV[16],表明在电场作用下中间神经元的胞体极化效应微弱,远小于锥体神经元的胞体极化作用.然而电场在中间神经元远端树突的膜电位极化作用较大,并且远端树突膜电位随电场强度变化而线性增加.

图3 海马CA1区中间神经元模型以及电场空间极化效应
1.3 亚线性树突计算分析方法
树突整合特性常用阈下输入-输出关系描述,即可以通过比较期望EPSP与观测EPSP之间的关系描述,其中多个突触输入同时激活所产生的胞体EPSP称为实际观测EPSP,而相同数目下依次激活的单个突触输入得到的胞体EPSP的代数和称为期望EPSP.当实际观测EPSP大于期望EPSP时,树突整合表现为超线性计算;当实际观测EPSP等于期望EPSP时,树突整合为线性计算;当实际观测EPSP小于期望EPSP时,树突整合表现为亚线性计算.
在中间神经元的一个树突分支施加AMPA突触刺激,突触位置如图4(a)所示,每个突触刺激位置用数字表示.实测EPSP为突触同时激活时胞体实际膜电压与静息膜电压的差值,期望EPSP为依次激活的单个突触激活产生的实测EPSP的代数和.突触刺激个数从1增大到6时得到实测和期望的胞体膜电压波形,分别如图4(a)和图4(b)所示.随着突触个数的增加,胞体膜电压增大的幅度逐渐减小,这是由于在树突为被动时对AMPA类型输入执行亚线性树突计算,如图4(c)所示.

图4 亚线性树突计算描述方法
2 结 果
2.1 亚线性树突整合动力学分析
奇异摄动系统是带有小参数的动态系统,具有多时间尺度的特点,其本质上是时间尺度分析法的一种近似解法.基于图1(c)单树突分支3间室等效电路模型,建立奇异摄动系统分析亚线性树突整合的动力学特性.为了探究中间神经元输入-输出关系之间的动力学机制,从而对由膜电位组成的状态向量引入一个扰动参数,将AMPA()看作奇异摄动系统的慢变量,Δms()看作快变量,由此构建奇异摄动系统为
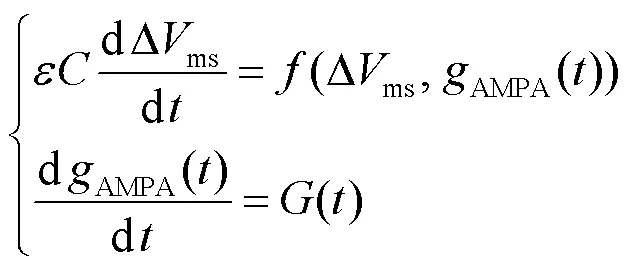
式中:为神经元膜电容;为摄动参数.依据变量时间尺度的不同,可由奇异摄动系统得到快子系统和慢子系统,通过把快、慢变量分开可把系统转化成低阶模型以方便分析.
AMPA突触电流表达式为
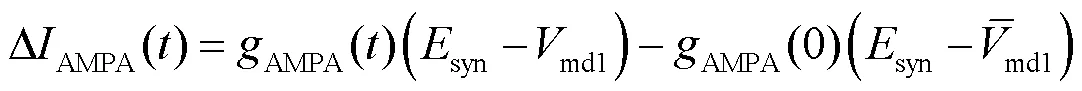
式中:syn为突触反电势,取值为0mV;AMPA(0)为AMPA突触电导初始状态,取值为0mS.AMPA突触电导随时间变化的表达式为
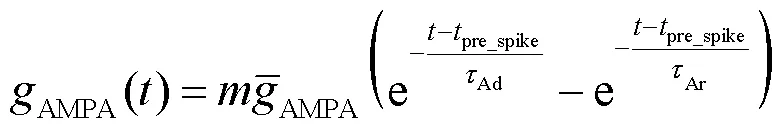
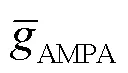
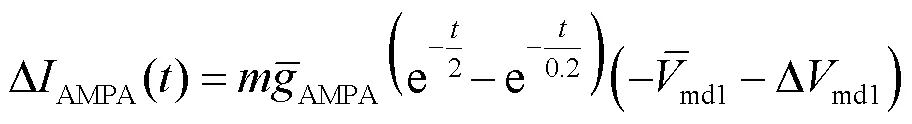

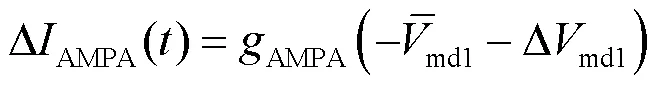
将式(14)结合状态方程(6)代入到奇异摄动系统方程(9)中,得到快子系统的状态方程为

根据快子系统的状态方程刻画其平衡点曲线,如图5(a)所示.在树突被动时,树突对AMPA突触输入进行亚线性积分,系统均为稳定的平衡点.设定AMPA突触电导的最小值为min,最大值为max,即AMPA()∈[min,max].快子系统中电导为常数,图5(a)中竖直的虚线为快子系统的一维动态过程,随着时间的变化膜电压在虚线上振荡,当快子系统时间尺度非常小时其收敛于稳定的平衡点.在慢子系统中突触电导是时变的并且随着时间增加而先增大再减小,当突触电导从min开始增大时,慢子系统动态跟随稳定的平衡点从点运动到点,此时电导和胞体膜电压达到最大值,而后随着时间的增大电导减小,慢流形沿着渐近平衡点曲线从点运动到点.图5(b)为亚线性树突整合时胞体膜电压的动态过程,其与图5(a)中的慢子系统动态相对应.

图5 亚线性树突整合动力学分析
树突整合动力学特性描述了神经元膜电位的动态曲线,并且突触电导也是时变的,在变化的过程中突触电导与膜电压的最大值为动力学特性的体现.而神经计算不考虑树突整合动力学特性,在描述阈下输入-输出关系时,刻画的突触电导与膜电压均为静态的,并且对应了树突整合动力学特性中的突触电导与膜电压的最大值.因此基于图1(c)单树突分支3间室等效电路模型,通过建立树突整合动力学与树突亚线性整合的联系来证明可以用渐近平衡点曲线描述中间神经元的阈下输入-输出关系.
将式(12)代入到系统状态方程(6)中,得到系统的动态微分方程为

令单个AMPA突触电导=10-6mS,远端树突静息膜电位为-64mV,采用Matlab求解式(16),得到胞体膜电压变化量ΔVms(t)的动态曲线.如图6所示,令膜电容C=1μF/cm2,当ε=0.2时,由于系统时间常数较大而造成延迟,因此AMPA突触电导gAMPA(t)与ΔVms(t)的曲线随时间t变化呈环状变化,gAMPA(t)到达最大值时ΔVms(t)并没有到达峰值.而在快子系统中慢变量gAMPA(t)为常数,取时变下突触电导gAMPA(t)的最大值gmax与ΔVms(t)的峰值ΔVmax作为特征值刻画快子系统的动态轨迹,描述摄动参数ε对神经元计算特性的影响(见图6(a)、(b)).当ε逐渐减小,ΔVms(t)能尽快到达峰值,快子系统越快并且越接近时的极限状态(见图6(c)).图6(d)中ΔV为ε的不同取值得到的胞体膜电位的变化量与平衡点电位的差值,可见ε越小,动态轨迹越接近渐近平衡点曲线.因此可以用快子系 统平衡点描述中间神经元的阈下亚线性输入-输出 关系.
2.2 亚线性输入-输出关系的渐近表达式
在快子系统中突触电导为常数,因此针对图2中的中间神经元多树突分支模型,式(7)中AMPA突触电流可以表示为

由于所有树突分支看作并联关系,因此每个分支的近端树突间室膜电压的变化量相同,并且由图1(c)可以得到近端树突与胞体膜电位变化量的关系,表示为
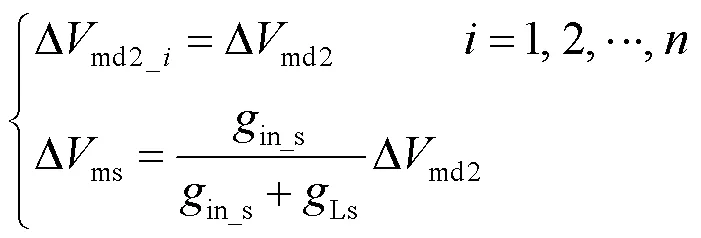
由式(8)、式(18)得到近端与远端树突膜电位变化量的关系为

此处考虑匀质情况,因此每个树突分支上的AMPA突触电导和远端树突静息膜电位相同,即

因此得到每个分支的远端树突膜电位变化量与分布突触刺激分支的电流保持不变,则有

由式(17)~式(21)得到胞体膜电位变化量与远端树突膜电位的变化量以及突触电流输入的表达式分别为

式中md、V11、V12、V2为常数,且其表达式分别为

由式(14)得到快子系统中AMPA突触电流表达式为

将式(24)代入到式(22)中,得到AMPA类型的中间神经元亚线性输入-输出关系渐近解析表达式为

设单个AMPA突触的最大电导为AMPA_s,单树突分支的突触电导可表示为

则多树突分支上的多个突触输入激活时,中间神经元胞体实际峰值膜电位的变化量为
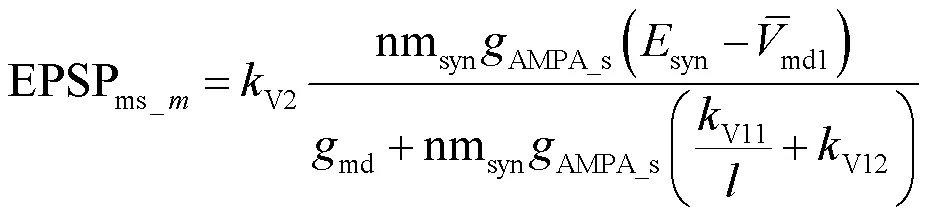
式中nmsyn为激活突触的全部数量,并且树突的总分支数,突触输入激活的树突分支数和nmsyn满足的条件和关系表达式为

根据式(24)得到单树突分支上的单个突触输入被激活时,中间神经元胞体EPSP为
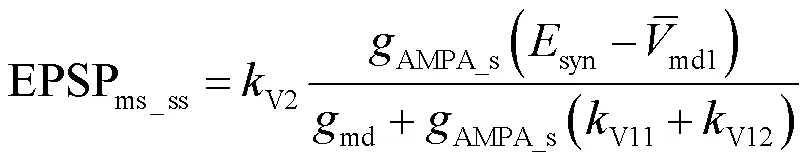
单树突分支上的个AMPA突触输入激活时,中间神经元胞体实际观测的EPSP表达式为

在单个树突分支上激活多个突触输入时,中间神经元胞体期望的EPSP为

在多个树突分支上的多个突触刺激下,中间神经元胞体期望的EPSP为

需要指出的是,分散的突触输入的树突末端在电场刺激下的极化作用与角度相关,因此本文得出的表达式可以描述分散分布的突触输入不对称情况下的树突整合.
2.3 树突静息电位对亚线性树突整合特性的影响
电场的空间极化效应使得中间神经元远端树突的静息膜电位发生改变,因此在简化电路模型中通过刻画中间神经元远端树突静息膜电位的变化来体现电场极化作用.根据上文得到的中间神经元的阈下亚线性输入-输出关系的渐近表达式,采用Matlab仿真研究电场极化对中间神经元树突亚线性整合特性的影响.模型中考虑全局和局部两种突触分布形式,如图7(a)与(b)所示,设置模型总分支数=10,远端树突静息膜电位为-64mV,AMPA的突触电导为10-6mS,两种分布下突触个数nmsyn均从0变化到80个.局部式突触分布为突触输入激活的远端树突的数量=1;全局式突触分布为=7.
利用式(30)与式(31)得到远端树突静息膜电位对局部亚线性树突整合的影响;根据式(27)和式(32)得到远端树突静息膜电位对非对称全局亚线性树突整合的影响,仿真结果如图7所示.依据胞体期望EPSP与实际观测EPSP的曲线关系,得出随着远端树突静息膜电位的增大,胞体饱和膜电位sat的变化规律.仿真结果表明AMPA突触输入下树突的全局与局部整合均随着突触刺激的增强,胞体膜电位最终达到饱和.全局与局部树突整合中发现相似的规律:中间神经元远端树突在正向电场超极化时静息膜电位降低,增强突触电流的驱动力进而弱化树突亚线性整合能力,使胞体输出增大;而在负向电场中远端树突去极化,静息膜电位升高,减小突触驱动力进而增强树突亚线性整合能力,使胞体输出减小.因此调制作用取决于中间神经元远端树突静息膜电位的变化,也就是依赖于电场的极性与强度改变.
通过对比全局与局部突触分布,研究电场极化对中间神经元全局与局部亚线性树突整合的敏感性,利用参数d衡量其调制的敏感性,d的计算方法为:对图7(c)与(d)中的直线求解其斜率的绝对值,表示单位远端树突膜电位变化下EPSP的变化量.电场极化作用主要体现在远端树突膜电位,并且电场强度与远端树突膜电位的变化关系近似线性,因此d越大说明电场极化对其调制效果越明显.仿真结果如图7(e)所示,表明全局树突整合得到的d远远大于局部树突整合得到的d,这是由于电场对中间神经元远端树突膜电位的极化呈同样趋势变化,即同时去极化同时超极化,使得电场对分散性突触输入的调制具有全局效应,对全局树突整合的调节更敏感.
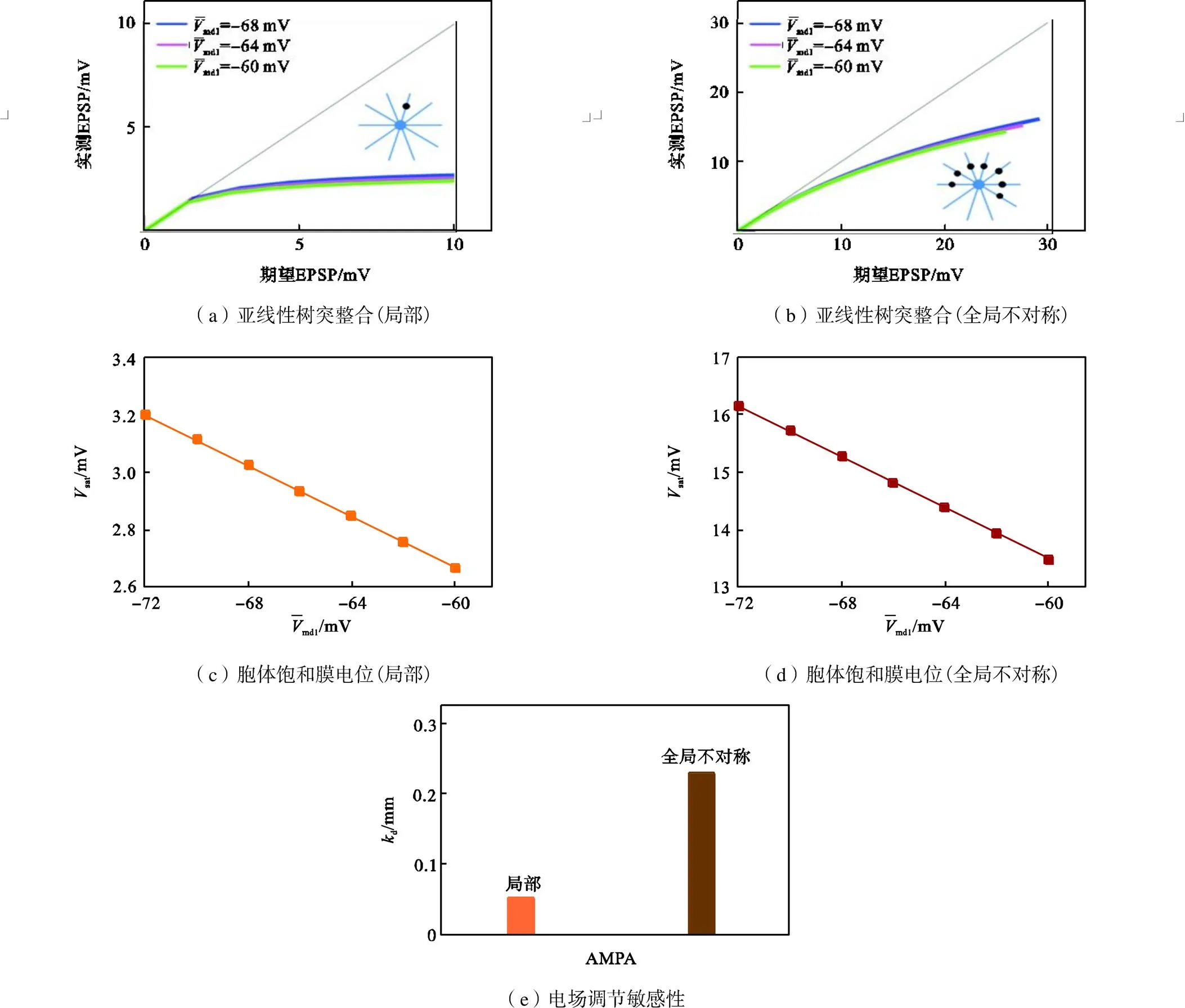
图7 远端树突静息电位对亚线性树突整合特性的影响
2.4 真实树突形态的中间神经元NEURON仿真
为了验证模型中电场极化对亚线性树突整合的理论预测,利用在海马区中间神经元电场模型中加入AMPA突触刺激进行分析.突触分布形式如图8(a)与(b)所示,局部式突触分布为突触随机分布在神经元的一个树突分支上,而全局式分布是指,突触随机分布在一部分树突上.在两种分布下突触个数从0增加到80个且在距离胞体大于60μm处同时激活,sat表示80个突触输入对应的实测EPSP(见图8(a)).为了衡量电场对中间神经元全局与局部亚线性树突整合调制的敏感性.将图8(c)中的点拟合成直线,Δ为=20V/m与=-20V/m对应的胞体EPSP峰值之差,Δ为电场变化量40V/m,树突增益dend的计算公式为
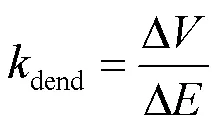
式中dend表示单位电场变化下胞体EPSP的变化量,树突增益越大说明电场对其调制效果越明显.以此方法计算单位电场变化时所引起的胞体极化膜电压的变化量,将图3(b)中的曲线拟合成直线并计算该直线的斜率,记为soma,结果见图8(d)中的蓝色柱体.
图8(a)和(b)中,当=20V/m时,电场使刺激端树突膜电位超极化而降低,增强了突触电流驱动力进而使AMPA类型的亚线性树突整合能力减弱,树突输入输出关系更加线性化,故sat增大;当= -20V/m时,电场作用下刺激端树突膜电位去极化而升高,降低突触电流驱动力使AMPA亚线性整合能力增强,树突输入输出关系亚线性化显著,故sat减小.因此电场强度从-20V/m以10V/m的步长增加至20V/m,sat随着电场强度的变化而增加(见图8(a)).观察树突增益发现,突触为全局分布时得到的树突增益远大于局部分布的树突增益,因此电场对中间神经元全局亚线性树突整合的调制更敏感,与理论简化模型结论一致.将突触分布不对称的情况(见图8(b))与对称情况(见图8(e))相比较,结果表明:当突触空间分布呈对称时,树突增益有较明显的下降(见图8(f)),说明对称性突触输入的整合对电场调节不敏感这一特性,与之前的研究表明电场对中间神经元调节效果不显著相一致.
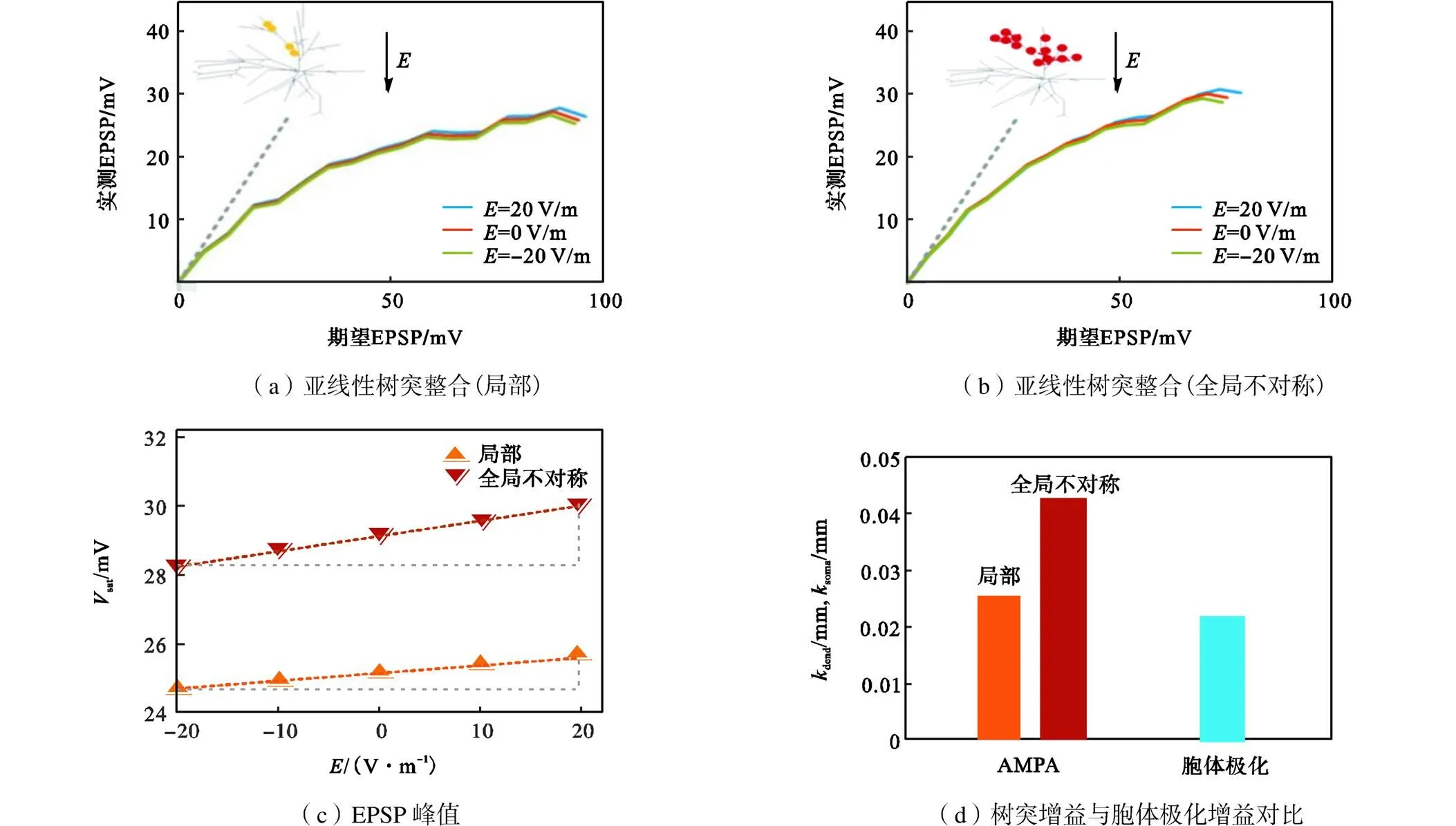
将树突增益与单位电场引起的胞体极化进行比较(见图8(d)),发现单位电场下的树突增益大约为胞体膜电位极化程度的2倍,因此电场通过极化远端树突膜电位引起的胞体膜电位变化量大于电场对胞体膜电位的极化,表明电场可以显著调节中间神经元的树突整合从而影响其胞体响应,并且分散的突触激活位置越不对称效果越显著.
目前研究表明同步激活的突触信号更有利于神经元信号整合[28],事实上突触并不是同时激活的.图8(g)和(h)分析了突触激活时间方差对电场调节亚线性树突整合的影响,其中asy表示激活时间方差,其值分别为0ms、20ms和100ms.由此发现突触激活时间方差相较突触分布对电场的调节作用影响微弱,但激活方差越大使突触输入之间的交互减弱,树突亚线性增强,因此神经元更难放电.与文献[28]结论 一致.
3 结 语
本文针对中间神经元单分支的多间室模型建立了奇异摄动系统,对AMPA类型的局部或全局树突亚线性整合进行了动力学分析,得到可描述中间神经元多树突分支的阈下输入-输出关系的渐近解析表达式.结果表明电场通过在中间神经元远端树突膜电位的极化作用,影响了AMPA突触电流驱动力,进而调节了中间神经元的全局与局部亚线性树突整合特性,调节作用依赖于电场的强度与极性,并且相比于局部树突整合,电场对全局树突整合的调制更敏感.利用真实树突形态的中间神经元模型进行NEURON仿真,从而验证模型结果.本文研究表明,即使中间神经元胞体极化作用微弱,但在突触激活位置不对称的情况下,电场调节下的中间神经元的树突积分会显著影响其胞体输出,从而影响神经元计算,此结果有助于理解电场调制中间神经元输入-输出功能的潜在机制,为阐释磁刺激技术调制脑功能的机理提供理论 基础.
[1] Isaacson J S,Scanziani M. How inhibition shapes cortical activity[J]. Neuron,2011,72(2):231-243.
[2] Shetty A K,Bates A. Potential of GABA-ergic cell therapy for schizophrenia,neuropathic pain,and Alzheimer’s and Parkinson’s diseases[J]. Brain Research,2016,1638:74-87.
[3] Southwell D G,Nicholas C R,Basbaum A I,et al. Interneurons from embryonic development to cell-based therapy[J]. Science,2014,344(6180):167-187.
[4] Amatniek J C,Hauser W A,DelCastillo-Castaneda C,et al. Incidence and predictors of seizures in patients with Alzheimer’s disease[J]. Epilepsia,2006,47(5):867-872.
[5] Shetty A K,Turner D A. Fetal hippocampal grafts containing CA3 cells restore host hippocampal glutamate decarboxylase-positive interneuron numbers in a rat model of temporal lobe epilepsy[J]. Journal Neuroscience,2020,20(23):8788-8801.
[6] Tyson J A,Anderson S A. GABAergic interneuron transplants to study development and treat disease[J]. Trends Neurosciences,2014,37(3):169-177.
[7] Guzman B C F,Vinnakota C,Govindpani K,et al. The GABAergic system as a therapeutic target for Alzheimer’s disease[J]. Journal of Neurochemistry,2018,146(6):649-669.
[8] Xu M Y,Wong A H C. GABAergic inhibitory neurons as therapeutic targets for cognitive impairment in schizophrenia[J]. Acta Pharmacologica Sinica,2018,39(5):733-753.
[9] Hallett M,Di lorio R,Rossini P M,et al. Contribution of transcranial magnetic stimulation to assessment of brain connectivity and networks[J]. Clinical Neurophysiology,2017,128(11):2125-2139.
[10] Ladenbauer J,Ladenbauer J,Kuelzow N,et al. Promoting sleep oscillations and their functional coupling by transcranial stimulation enhances memory consolidation in mild cognitive impairment[J]. The Journal of Neuroscience,2017,37(30):7111-7124.
[11] Huang Y,Liu A A,Lafon B,et al. Measurements and models of electric fields in thehuman brain during transcranial electric stimulation[J]. ELife,2017,6:1-26.
[12] 于 凯,王 江,邓 斌,等. 磁刺激作用下感生电场对网络同步的影响[J]. 天津大学学报(自然科学与工程技术版),2013,46(8):726-736.
Yu Kai,Wang Jiang,Deng Bin,et al. Effects of induced electric field on network synchrony under magnetic stimulation[J]. Journal of Tianjin University(Sci-ence and Technology),2013,46(8):726-736(in Chinese).
[13] Bikson M,Inoue M,Akiyama H,et al. Effect of uniform extracellular DC electric fields on excitability in rat hippocampal slices[J]. Journal of Physiology-London,2004,557(1):175-190.
[14] Radman T,Su Y Z,An J H,et al. Spike timing amplifies the effect of electric fields on neurons:Implications for endogenous field effects[J]. Journal of Neuroscience,2007,27(11):3030-3036.
[15] Reato D,Rahman A,Bikson M,et al. Low-intensity electrical affects network dynamics by modulating population rate and spike timing[J]. Journal of Neuroscience,2010,30(45):15067-15079.
[16] Radman T,Ramos R L,Brumberg J C,et al. Role of cortical cell type and morphology in subthreshold and suprathreshold uniform electric field stimulation[J]. Brain Stimulation,2009,2(4):215-228.
[17] Jackson M P,Rahman A,Lafon B,et al. Animal models of transcranial direct current stimulation:Methods and mechanisms[J]. Clinical Neurophysiol-ogy,2016,127(11):3425-3454.
[18] Murphy S C,Palmer L M,Nyffeler T,et al. Transcranial magnetic stimulation(TMS) inhibits cortical dendrites[J]. Elife,2016,5:1-12.
[19] Stuart G J,Spruston N. Dendritic integration:60 years of progress[J]. Nature Neuroscience,2015,18(12):1713-1721.
[20] Stafford J,Brownlow M L,Qualley A,et al. AMPA receptor translocation and phosphorylation are induced by transcranial direct current stimulation in rats[J]. Neu-robiology of Learning and Memory,2018,150:36-41.
[21] Abrahamsson T,Cathala L,Matsui K,et al. Thin dendrites of cerebellar interneurons confer sublinear synaptic integration and a gradient of short-term plasticity[J]. Neuron,2012,73(6):1159-1172.
[22] Vervaeke K,Lorincz A,Nusser Z,et al. Gap junctions compensate for sublinear dendritic integration in an inhibitory network[J]. Science,2012,335(6076):1624-1628.
[23] Tran-Van-Minh A,Caze R D,Abrahamsson T,et al. Contribution of sublinear and supralinear dendritic integration to neuronal computations[J]. Frontiers in Cellular Neuroscience,2015,9:1-15.
[24] Poleg-Polsky A. Effects of neural morphology and input distribution on synaptic processing by global and focal NMDA-spikes[J]. PLoS One,2015,10(10):1-21.
[25] Hines M L,Carnevale N T. The NEURON simulation environment[J]. Neural Computation,1997,9(6):1179-1209.
[26] Saraga F,Wu C P,Zhang L,et al. Active dendrites and spike propagation in multi-compartment models of oriens-lacunosum/moleculare hippocampal interneurons[J]. Journal of Physiology-London,2003,552(3):673-689.
[27] 伊国胜,王 江,魏熙乐,等. 无创式脑调制的神经效应研究进展[J]. 科学通报,2016,61(8):819-834.
Yi Guosheng,Wang Jiang,Wei Xile,et al. Developments of neural effects induced by noninvasive brain modulation[J]. Chinese Science Bulletin,2016,61(8):819-834(in Chinese).
[28] Li Xiumin. Signal integration on the dendrites of a pyramidal neuron model[J]. Cognitive Neurodynamics,2014,8(1):81-85.
Modulation Effect of Electric Fields on Sublinear Dendritic Integration of the Interneuron
Wei Xile,Fan Yaqin,Zhao Meijia,Yi Guosheng,Wang Jiang
(School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China)
Most studies have suggested that the modulatory effect of the electrical field (EF) on the interneuron can be ignored due to the EF-induced weak somatic polarization that results from the symmetric distribution of dendritic morphology. However,EF induces strong polarization at distal dendritic spines of the interneuron. Whether and how these polarizations at the distal dendrites partake in the dendritic integration of alpha-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) synapses remain unclear. In this regard,a simplified circuit model with multiple passive dendritic branches was established to capture the dendritic input-output relationship of the interneuron receiving asymmetrically distributed AMPA synapses,in which the inhomogeneous extracellular potentials characterize EF-induced polarizations. The dynamics of sublinear dendritic integration of interneuron were analyzed based on the singular perturbation theory. Our theoretical results showed that the EFs regulated the local and global sublinear dendritic integration properties of the interneuron by altering the driving force of AMPA synaptic inputs,depending on the degree of polarization at the distal dendrites. Additionally,the EF-regulated effect on global dendritic integration has higher efficiency compared to local dendritic integration. The simulation of an interneuron model with realistic dendritic morphology at the hippocampal CA1 in the case of EF stimulation verified the results of theoretical analysis.
interneuron;electric field;polarization;sublinear dendritic integration
10.11784/tdxbz202012009
Q64
A
0493-2137(2022)02-0199-12
2020-12-04;
2021-04-06.
魏熙乐(1975— ),男,博士,教授,xilewei@tju.edu.cn.Email:m_bigm@tju.edu.cn
伊国胜,guoshengyi@tju.edu.cn.
国家自然科学基金资助项目(61771330,62071324);天津市自然科学基金资助项目(19JCQNJC01200).
the National Natural Science Foundation of China(No.61771330,No.62071324),the Natural Science Foundation of Tianjin,China(No. 19JCQNJC01200).
(责任编辑:孙立华)

