基于遗传算法的转管武器凸轮曲线优化设计

于家辉,王惠源,张成卿,王程伟,汪前进

(1.中北大学 机电工程学院,太原 030051; 2.昆仑工业(集团)有限责任公司, 西安 710043)

1 引言

转管武器自动机设计过程中，机心上主滚轮与凸轮曲线槽相配合，凸轮曲线的设计对于自动机的性能好坏起着决定性作用。为提高自动机性能，需要设计出转管武器自动机凸轮机构的轮廓曲线。对于转管武器的凸轮曲线，通过比较正弦曲线和梯形曲线的性能参数，确定了从单纯的正弦曲线变为在正弦曲线中插入一段二次曲线的形式，降低了加速度和跃度，在进一步的研究中，也出现了取消斜直线段，通过平分角度来设计凸轮曲线，徐健等又通过增加其过渡段角度，减小前直线段对应角度从而对凸轮性能进行了改进，后来也通过应用3次样条进行改进，获得了改进结果；李世康等通过应用5次曲线代替正弦曲线；李强等使用线性加权法优化修正正弦曲线，其方法通过对优化变量施加权重系数来实现，在优化自动机的过程中，应用模拟退火算法和线性加权法对自动机结构进行优化；熊镐等应用线性规划方法优化凸轮曲线，线性加权法优点在于优化方法简单，可通过应用优化求解工具箱直接求解，但易陷入局部最优解，在加速度下降的同时跃度上升，在降低机心与凸轮曲线的撞击力的同时振动加剧，不能满足工程中对于高速凸轮应具有优良综合性能的要求。

葛荣雨等提出应用遗传算法进行凸轮曲线的多目标优化，本文运用理想点法建立优化的理论模型，按照转管武器凸轮机构的工作要求，应用遗传算法求解，分配过渡段角度及其推程，从而在降低机心和凸轮曲线撞击力、提高机心和凸轮曲线寿命的同时，降低机心跃度和电机驱动功率，优化设计出凸轮轮廓。

2 曲线槽与机心运动

2.1 凸轮曲线与机心运动

由多根身管组成的转管武器具有多个机心，机心上主滚轮与凸轮曲线槽相配合，从而完成装弹、推弹、击发、抛壳的动作。

图1为转管武器机心的理论运动轨迹。、、、为曲线过渡段，、为前直线段和后直线段，、为斜直线段，为机心推程，、为过渡段的轴向长度。

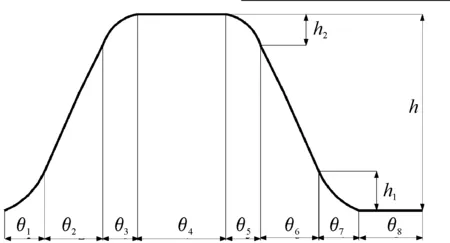
图1 转管武器机心的理论运动轨迹Fig.1 Diagram of the theoretical movement trajectory of Gatling gun movement

2.2 修正正弦加速度曲线槽

图2为修正正弦加速度曲线。修正正弦加速度曲线由2段正弦曲线(、)、2次曲线()拼接而成。

图2 修正正弦加速度曲线Fig.2 Modified sine acceleration curve constitute

正弦曲线()的位移、类速度、类加速度、类跃度为：

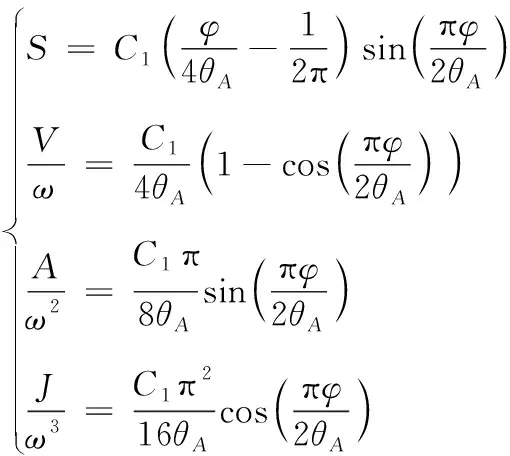
(1)

2次曲线()段为：

(2)

正弦曲线()段为：

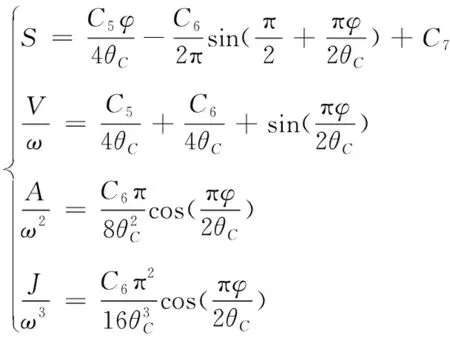
(3)

式(1)～(3)中，为凸轮的角速度。

2条正弦曲线和2次曲线所占角度的分配关系为：

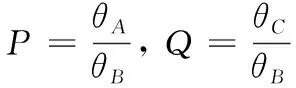
(4)

整理后：

=2

(5)

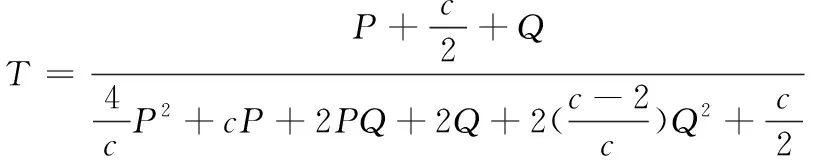
(6)

同时根据拼接条件，修正段的凸轮转角、与其对应的机心位移量、的关系式为：

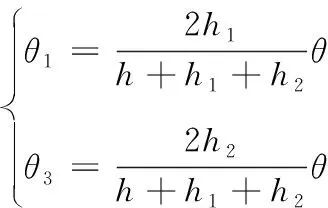
(7)

或

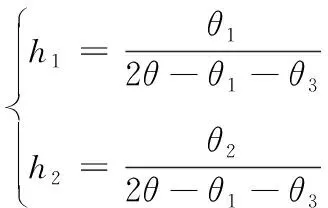
(8)

3 遗传算法优化计算设计

遗传算法抽象于生物体的进化过程，通过全面的模拟自然选择和遗传机制，形成的一种具有“生成+检验”特征的搜索算法。遗传算法以编码空间代替问题的参数空间，以适应度函数为评价标准，以编码群体为进化基础，以对群体中个体位串的遗传操作实现选择和遗传机制，建立起一个迭代过程。在这一过程中，通过随机重组编码位串中重要的基因，使新一代的位串集合优于老一代的位串集合，群体的个体不断进化，逐渐接近最优解，最终达到求解问题的目的。在遗传算法(GA)的应用过程中，往往结合问题特征和领域知识对标准遗传算法(SGA)进行各种改变，形成各具特色的GA，使得GA具有求解不同类型问题的能力，以及强大的全局搜索能力。遗传算法流程如图3所示。

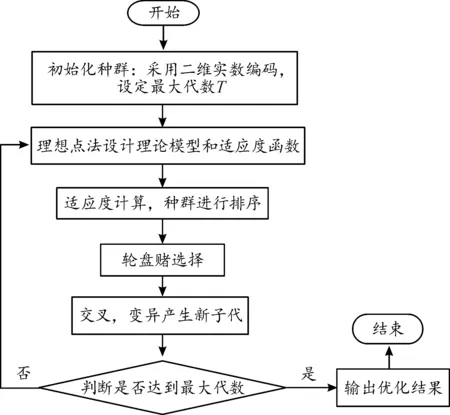
图3 遗传算法流程框图Fig.3 Flowing diagram of genetic algorithm

3.1 优化目标

由转管武器的动力性能优化目标如下：

1) 机心最大速度：机心最大速度和压力角成正比，影响传动效率。

2) 机心最大加速度：根据自动机动力学，加速度和机心与曲线槽的碰撞力大小成正比，直接影响机心使用寿命。

3) 机心最大跃度：在转管武器高射速情况下，机心的跃度影响机心的振动和冲击。

凸轮曲线槽和机心的横越冲击速度为：

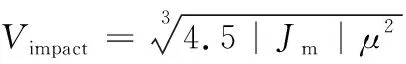
(9)

式(9)中，为间隙值。

4) 最大无量纲惯性矩：在转管武器达到稳定射频时，电机的驱动功率和最大无量纲惯性矩相关，根据驱动功率选取适合的电机。

=AV

(10)

3.2 种群编码与初始化

由于凸轮曲线性能优化属于二维优化变量，编码方式采用实数编码，整体凸轮曲线采用对称结构，因此一种可行的编码方式[(，)，(，)，…，(，)],获得一个规模为的初始种群。

3.3 选择方法

需要对优秀的个体进行筛选，采用轮盘赌选择方法，假设在种群中某个个体的适应度的,则被选中的概率为：

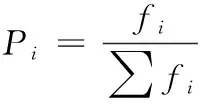
(11)

3.4 适应度计算方法

机心的最大速度、最大加速度、最大跃度之间并不是独立存在，相互之间存在联系，所以为了获得更好的优化效果，需要基于多目标优化的思想来解决问题。有学者使用线性加权方法进行优化，但线性加权方法的权重系数并没给出完整且合理的分配，结果也往往优化有限。这里使用理想点法，将多目标优化转化为单目标优化函数，令其成为遗传算法中的适应度函数，获得优化结果并和使用线性加权法的结果进行比较来判断方法的优劣。

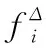
通过这种方法把多目标优化变为单目标优化，把求解最小函数值函数变为求解各值逼近最优解程度的函数，解决了最小函数值问题中、、之间量纲不同所带来的问题。

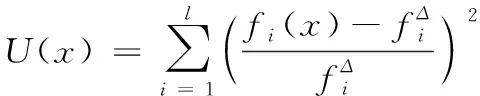
(12)

修正段的凸轮转角、与其对应的机心位移量、的关系式如下。

修正正弦曲线为：

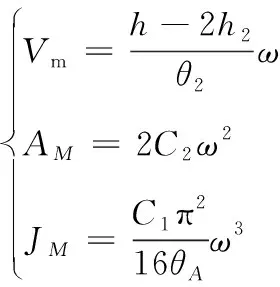
(13)

各变量在该条件下的最小值为：

(14)

构造目标函数为：

(15)

故该转管武器的凸轮优化模型为：

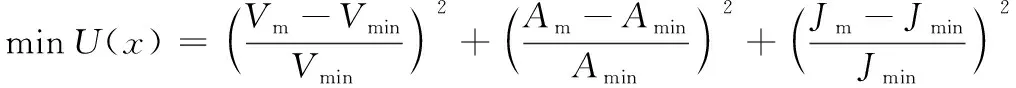
(16)

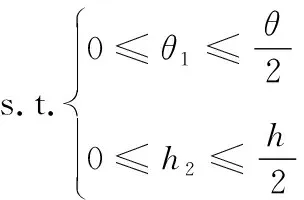
(17)

3.5 交叉和变异操作

交叉和变异操作能扩展新的搜索空间，帮助跳出局部最优解，增加种群多样性。

交叉方式由父代个体A、B提供第个基因进行交叉计算产生新个体，即：

=+(1-)

(18)

式(18)中，为区间(0,1)的随机数。

变异操作为加上一随机数，即：

=+

(19)

4 优化结果对比

现阶段，针对转管武器凸轮曲线优化主要方法为线性加权法，通过人为施加权重系数，建立理论模型，应用最优解优化工具箱求解，本文与该方法的优化结果进行对比。

利用遗传算法优化6管6 000发/min的转管武器凸轮曲线，选出文献[7]中每一种权重分配中的修正正弦加速度曲线，和本研究优化的3条曲线共计5条曲线进行比较。

文献[7]中的曲线分别为Case 1、Case 2；本研究优化的3条曲线分别为Case 3、Case 4、Case 5。

本文采用理想点法进行适应度函数的编写，没有针对单一或几个变量，而是求取全局最优解，因为过渡段角度和推程越相似，其性能特性也更相似，根据各曲线的过渡段所占角度和推程数值大小相似度匹配对比对象,故选用Case 3和Case 1、Case 4、Case 5和Case 2进行对比。各曲线角度分配关系如表1所示。

由于转管武器的供弹、击发等功能的要求，各工作区间角度已进行分配，从图4中凸轮曲线形状可以看出，优化前后的凸轮曲线整体结构没有发生变化，凸轮曲线在优化后对转管武器其他结构没有影响。

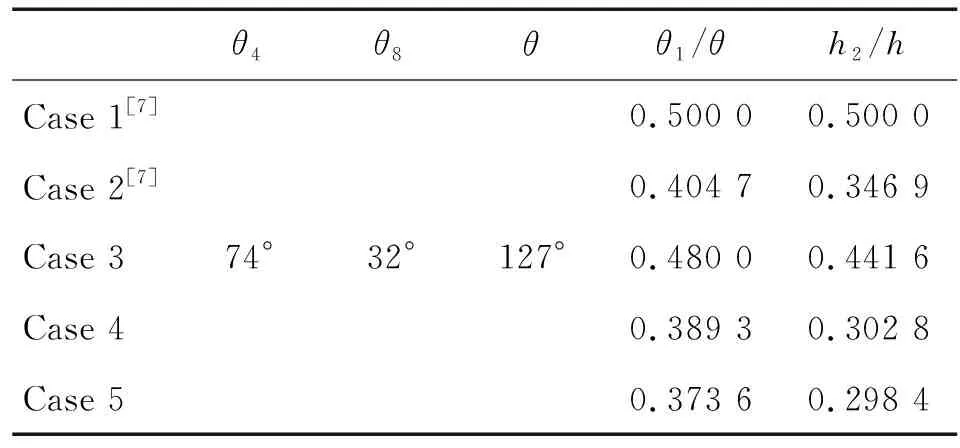
表1 凸轮曲线角度分配Table 1 Angle distribution of cam curve

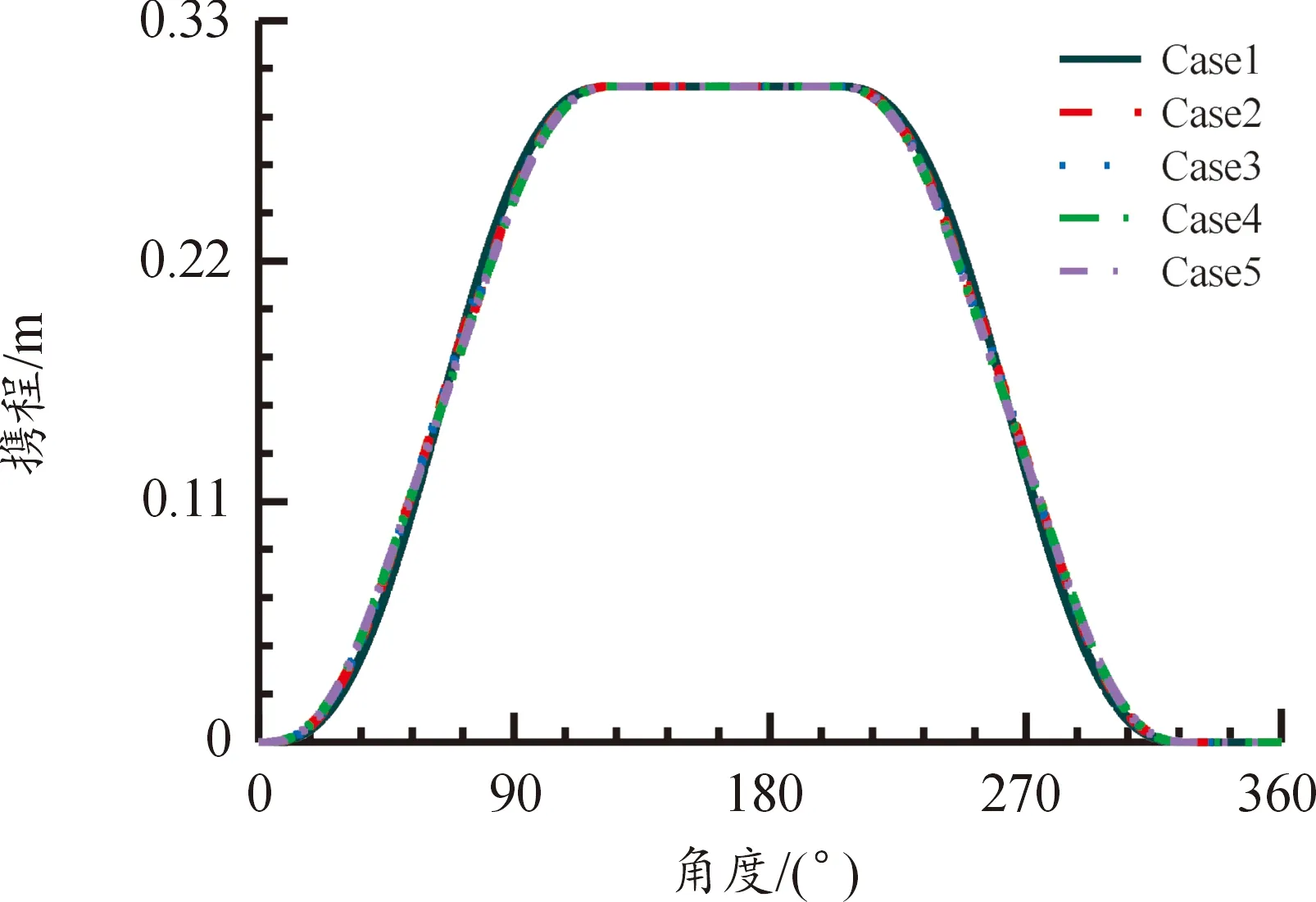
图4 转管武器凸轮曲线Fig.4 Cam curve of the Gatling gun

优化后的Case 3相比于Case 1最大速度下降7.80%，速度的下降提升了传动效率。Case 4、Case 5相比于Case 2最大速度分别下降0.10%、0.60%，速度的下降降低了最大压力角，在转管武器高射速、高转速的情况下，提升了自动机的传动效率。各曲线速度变化情况如图5所示。

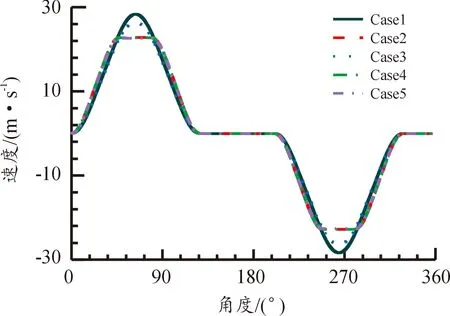
图5 速度曲线Fig.5 Velocity of different curves

优化后的Case 3相比于Case 1最大加速度下降4.03%，Case 4、Case 5相比于Case 2最大加速度分别下降1.83%、1.37%。最大加速度下降，机心主滚轮和凸轮曲线槽之间由于存在间隙故而会发生碰撞，最大加速度下降，机心主滚轮与凸轮曲线槽之间的最大冲击力减小，降低机心主滚轮与凸轮曲线槽之间的磨损，延长机心和凸轮曲线槽的使用寿命。各曲线加速度变化情况如图6所示。

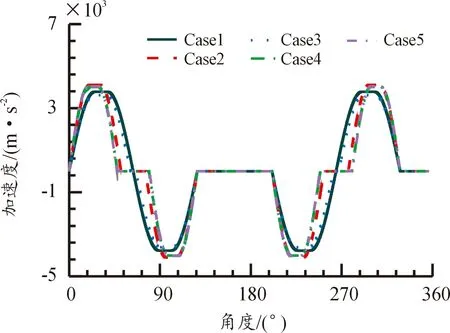
图6 加速度曲线Fig.6 Acceleration curve

优化后的Case 3相比于Case 1最大跃度下降0.50%，Case 4、Case 5相比于Case 2最大跃度分别下降20.33%、19.18%。在转管武器超高射频的情况下，凸轮曲线槽和机心的横越冲击速度减小，振动降低。各曲线跃度变化情况如图7所示。

图7 跃度曲线Fig.7 Jerk curve for different

优化后的Case 3相比于Case 1最大无量纲惯性矩下降11.78%，Case 4、Case 5相比于Case 2最大无量纲惯性矩分别下降1.90%、1.97%。最大无量纲惯性矩直接反应对于外能源驱动电机功率的要求，降低电机的驱动功率，扩大电机选择范围。各曲线计算结果如表2所示。

通过以上各曲线速度、加速度计算得出对应机心滚轮正应力变化情况如图8所示。

在各峰值下降的同时，优化后的Case 3相比于Case 1，最大正压力由34 433 N下降为31 845 N，下降7.51%，Case 4、Case 5相比于Case 2，最大正压力由36 339 N分别下降为30 646 N和30 634 N,分别下降15.66%、15.69%，降低机心滚轮正压力，减少机心主滚轮与凸轮曲线槽之间的磨损，延长机心和凸轮曲线槽的使用寿命。

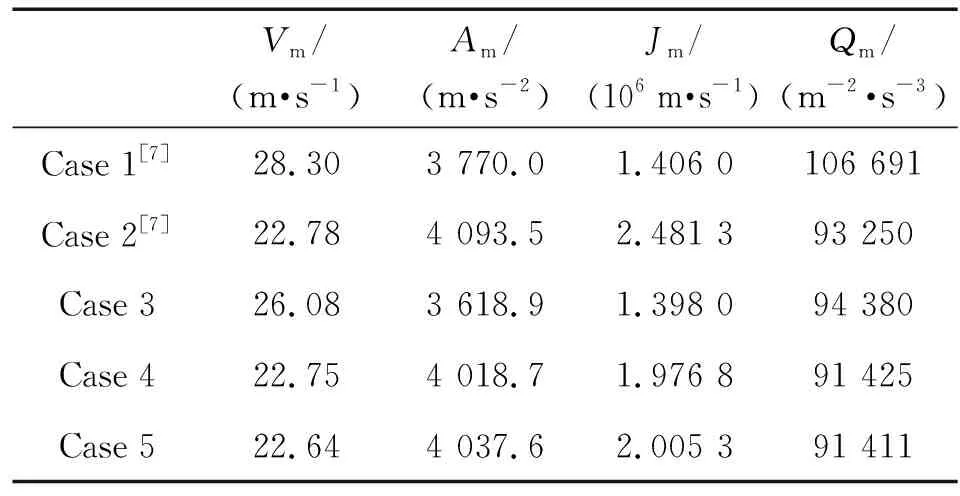
表2 各曲线计算结果Table 2 Calculation results of each curve

图8 正应力曲线Fig.8 Normal force curve

5 结论

将遗传算法应用于优化转管武器凸轮曲线，通过遗传算法对优化模型进行求解。针对修正正弦加速度转管武器凸轮曲线进行优化，并和现有线性加权法的优化结果进行比较，Case 3相比于Case 1在最大跃度下降的同时，最大加速度、速度、无量纲惯性矩，机心滚轮正应力下降明显；Case 4、Case 5相比于Case 2，在最大速度和加速度小幅下降的同时，最大跃度、机心滚轮正应力下降明显，降低机心滚轮与凸轮曲线槽之间的撞击和振动；相比于线性加权法人为施加权重系数，该方法则是通过种群适应度计算等操作不断接近全局最优解，得出的结果更加合理，取得了更加优秀的凸轮曲线。