基于多岛遗传算法的舱口盖结构优化设计
周玉松, 姜春光, 齐克学, 胡 胜,刘森峻*, 杨利春, 牟宗宝, 于 群, 徐 冰
(1.大连船舶重工集团设计研究院,辽宁 大连 116006;2.中船(天津)船舶制造有限公司,天津 300452)
0 引 言
在某船舱口盖结构初始设计方案中,舱口盖板厚度较薄,总体结构偏弱,通过计算表明不符合规范要求,某个部位应力一旦超过许用值,会导致局部构件失效,而局部的构件失效可能导致船体结构整体失效,将进一步导致较为严重的后果。若简单将舱口盖板板厚和加强筋腹板板厚加厚,虽可能会满足规范要求,但会导致较多结构质量的增加,因此有必要对舱口盖结构进行优化设计。
舱口盖结构设计的变量包括舱口盖板板厚,纵向加强筋的间距和剖面特性,横向加强筋的间距和剖面特性。若加强筋不采用等间距布置,则应考虑各加强筋距离参考点的位置。因此,舱口盖结构设计是一个典型的离散变量组合优化问题。尽管舱口盖结构相对于全船结构设计范畴较小,但进行优化设计的变量组合仍十分可观。
近年来,国内外学者在舱口盖结构优化设计方面进行很多研究。田阿利等[1]提出使用钢聚氨酯夹层板代替传统舱口盖所用的钢质板架,采用基于Box-Behnken设计的响应面法进行结构多目标优化设计。刘俊梅等[2]对1艘5 000 t散货船舱口盖的结构强度进行有限元计算分析,对影响结构强度的关键部位进行加强。王明强等[3]采用基于均匀法的拓扑优化方法对舱口盖横梁腹板和纵桁腹板进行优化设计。刘文涛等[4]研究不同板厚对舱口盖强度的影响,对舱口盖结构强度进行优化。李辉程[5]对1艘多用途集装箱船的舱盖强度进行有限元计算分析,并分析优化加强方案。徐双喜等[6]对舱口盖周围水平限位器和支撑块处的约束及顶部压紧器处的关联程度进行模拟,对其在垂向设计载荷情况下对舱口盖应力分布的影响进行分析,得到更符合实际情况的舱口盖结构强度计算方法。王贵彪等[7]对某鱿鱼钓船舱口盖结构建立有限元模型,分析在风雨密和自重载荷条件下的结构强度。
目前的舱口盖优化设计研究主要关注板厚优化和拓扑优化,项目采用响应面法建立舱口盖结构强度与设计参数的近似模型,以结构质量最小为目标函数,采用多岛遗传算法进行结构优化,可得到在工程上可行的结构优化设计方案。
1 优化设计问题
某船舱口盖结构初始设计方案如图1所示。舱口盖为典型的板梁结构,由面板、横梁和纵桁组成。舱口盖长为2.2 m,宽为1.5 m,圆角半径为200.00 mm,设置2根纵桁和4根横梁。全船共8个舱口盖,每个舱口盖设置8个锁紧装置,锁紧装置通过螺母压紧压板。舱口盖与舱口围板之间配置弹性填料。
舱口盖主要构件尺寸为:盖板厚度7.00 mm;纵桁(T型材)(50.00 mm×6.00 mm)/(90.00 mm×6.00 mm);横梁(扁钢)50.00 mm×6.00 mm;肘板40.00 mm×40.00 mm×6.00 mm;内缘扶强材(扁钢)40.00 mm×6.00 mm;腐蚀裕量2.00 mm。
根据中国船级社(CCS)《钢质海船入级规范—2021》(下文简称“规范”)要求,舱口盖垂向露天设计载荷为24.91 kN/mm2。在舱口盖初始设计方案中,质量为230.6 kg。
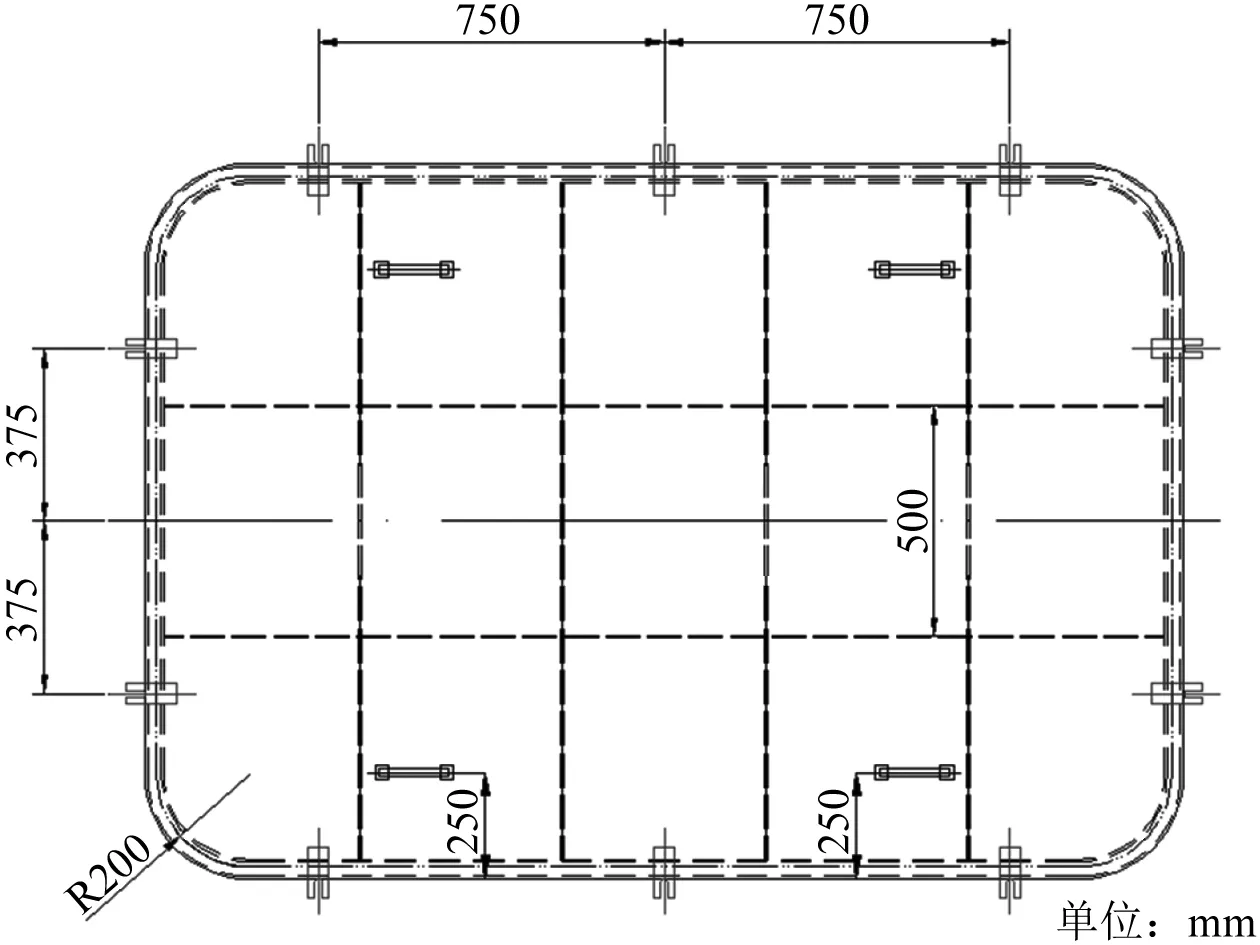
图1 舱口盖结构初始设计方案
根据舱口盖特点,舱口盖设计变量可分为布置参数和截面参数两类。布置参数包括纵桁与横梁的数量及间距。截面参数包括盖板的厚度和纵桁与横梁的截面尺寸,截面参数必须按照国标选择,因此截面参数属于离散变量。
舱口盖结构优化设计问题可描述为求X={x1,x2,…,xK},即
minW=f(x1,x2,…,xK)
s.t.σvM≤[σ]
s≤[s]
xmin≤xi≤xmax
(1)
式中:W为舱口盖质量,可由设计参数求得;x为设计变量;K为设计变量总数;σvM为当前结构最大von Mises应力;s为结构最大变形;xmin和xmax分别为设计变量xi的上下限。
2 优化设计方法
根据舱口盖初始方案,布置参数中的间距与纵桁和横梁的数量相关。每增加1个横梁,就会增加1个间距。参考母型船设计资料,将纵桁数量控制在3根内、横梁数量控制在5根内。布置参数的总数如下:
方案一:纵桁1根、横梁3根,设计变量1个。
方案二:纵桁1根、横梁4根,设计变量2个。
方案三:纵桁1根、横梁5根,设计变量3个。
方案四:纵桁2根、横梁3根,设计变量2个。
方案五:纵桁2根、横梁4根,设计变量3个。
方案六:纵桁2根、横梁5根,设计变量4个。
方案七:纵桁3根、横梁3根,设计变量2个。
方案八:纵桁3根、横梁4根,设计变量3个。
方案九:纵桁3根、横梁5根,设计变量4个。
对于截面参数,板厚取值为5.00~8.00 mm;扁钢及纵桁腹板高度取值为30.00~100.00 mm;纵桁面板宽度取值为30.00~80.00 mm;步长均为0.50 mm。
在设计域内将上述设计变量组合起来,可行方案的数量较多,难以求解。遗传算法和粒子群优化算法等智能算法是解决组合优化问题的有效工具,而多岛遗传算法是近年来发展的一种改进遗传算法。该算法将传统遗传算法的种群分解为多个岛屿,每个岛屿存在若干个体,个体可在岛屿间迁移,这样可避免陷入局部最优而达到全局最优。多岛遗传算法的种群生成原理如图2所示。
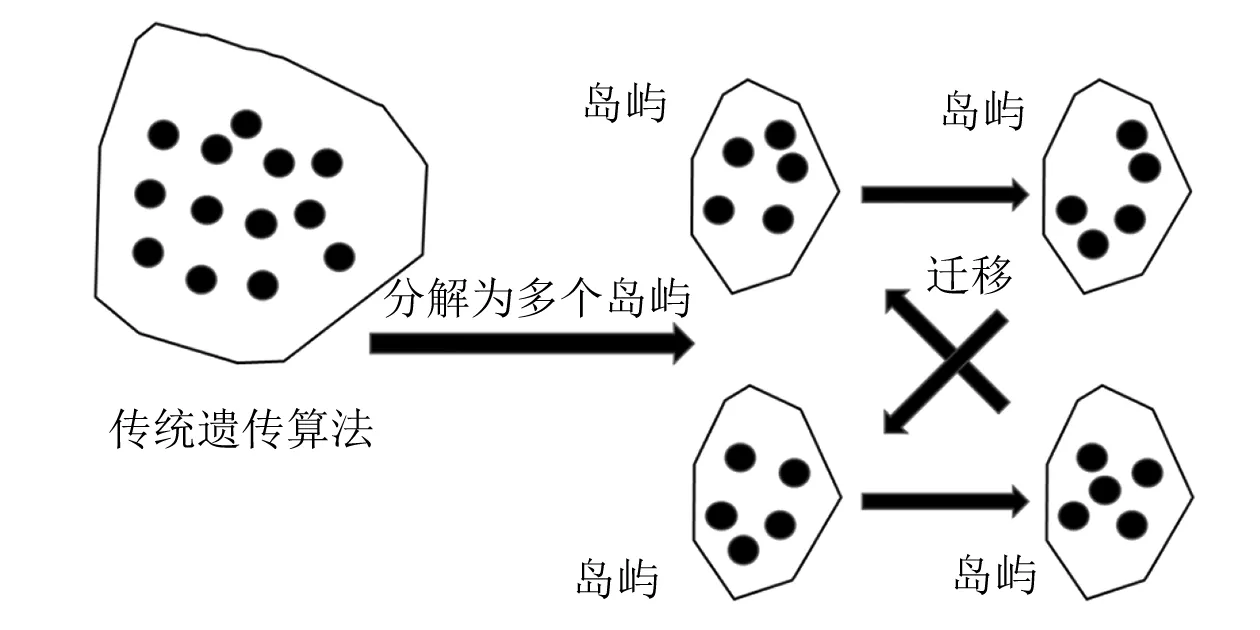
图2 多岛遗传算法的种群生成原理
与其他遗传算法一样,多岛遗传算法基于目标函数的值和约束代价,每个设计点均被视为具有一定适用性的个体,而具有更好的目标函数值和更好的罚分值的个体具有更高的适应度值。与传统遗传算法的区别在于,多岛遗传算法的主要特征是个体被分为数个称为“岛屿”的子种群,所有传统的遗传操作均在每个子种群上分别执行,从每个岛屿中选出一些个体,并定期迁移至不同的岛屿。多岛遗传算法迭代过程如图3所示。参数控制迁移过程分为2个:迁移间隔,即每次迁移之间的世代数;迁移率,即在迁移时从每个岛屿迁移的个体百分比。
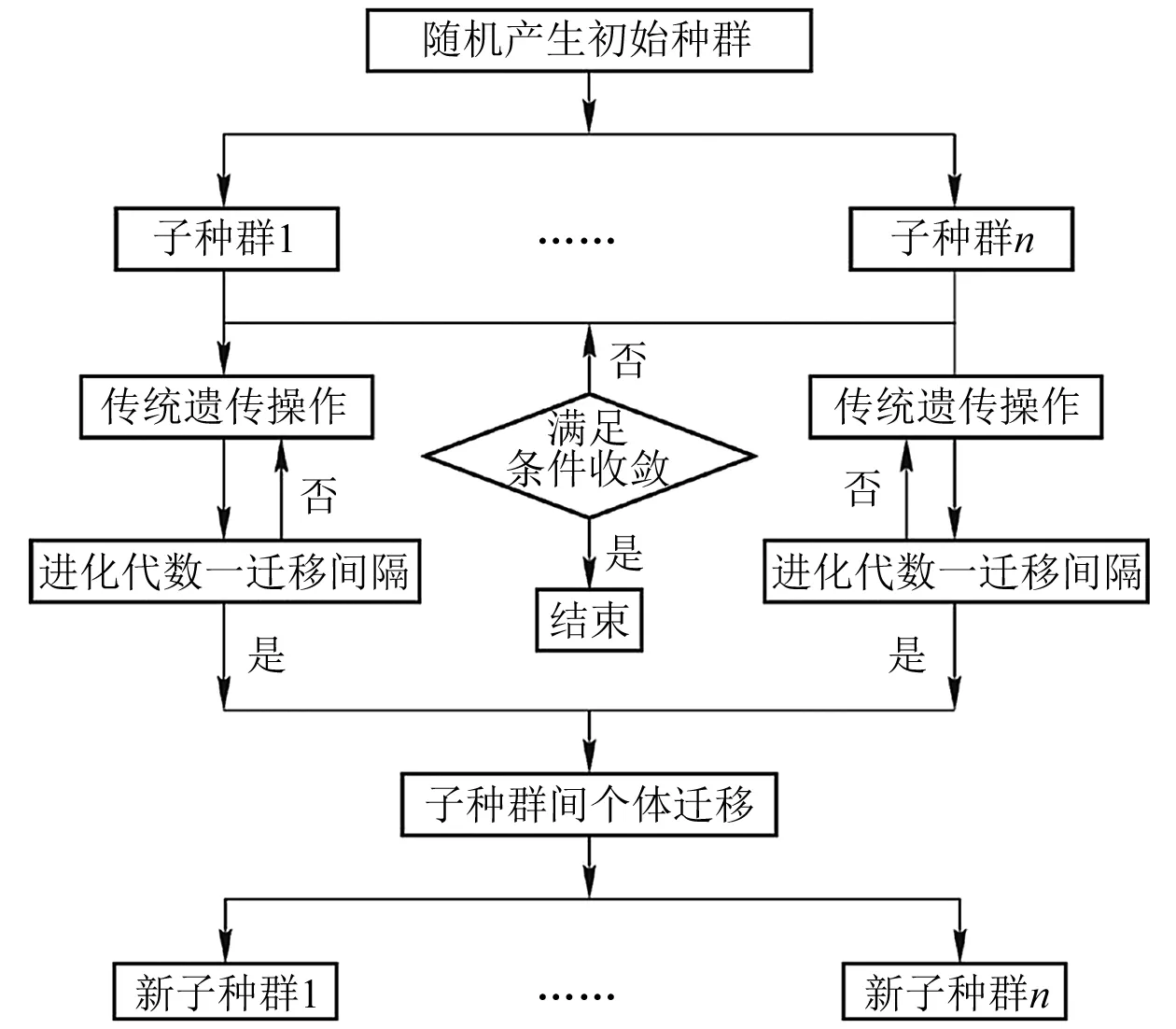
图3 多岛遗传算法迭代过程
3 结构优化过程
3.1 建立近似模型
近似模型技术通过对已知数据中的输入变量和输出变量进行数学建模,给出一个可近似反应输入变量与输出变量之间关系的模型,减少各类专业领域中的复杂试验和仿真等分析过程。常用的近似模型技术主要包括响应面法、径向基法和克里金法。近似模型的输入变量和输出变量的关系可表示为
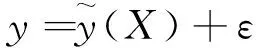
(2)
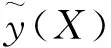
通常,输入变量与输出变量之间的关系为非线性,舱口盖结构设计问题同样如此,项目选择响应面法对目标函数(舱口盖结构质量)和设计参数进行建模。根据设计变量的取值范围设置样本空间,采用拉丁方试验设计方法进行采样,根据样本参数进行有限元模型求解,得出结构质量、最大应力和最大变形。
采用ANSYS作为有限元求解软件,通过VB编程语言(Visual Basic,VB)二次开发实现自动调用样本参数进行有限元求解及提取结果的程序。以某组设计变量为例,说明有限元求解的结果。舱口盖的盖板、内缘扶强材、横梁腹板、纵桁面板、纵桁腹板和肘板等构件为平面板,采用一次壳单元SHELL63建模;横梁面板采用线性梁单元BEAM188建模。舱口盖有限元模型如图4所示。模型的节点总数为4 065,单元总数为4 003,其中:SHELL63总数为3 835;BEAM188总数为168。

图4 舱口盖有限元模型
根据规范对边界条件的要求,项目边界条件设置如下:在锁紧装置处约束z向的位移,δz=0;在宽度方向的锁紧装置处约束x向的位移,δx=0;在长度方向的锁紧装置处约束y向的位移,δy=0。节点约束如图5所示。

图5 节点约束
作用于模型的载荷主要为设计载荷和重力载荷。设计载荷为面载荷,施加于舱口盖板。重力载荷通过指定重力加速度(ACEL命令)实现。
材料的上屈服强度ReH对应的屈服应力为235.0 MPa,材料的换算系数K取1。根据规范要求,基于净尺寸的舱口盖结构等效应力应不大于0.8ReH。
根据规范要求,采用细化网格,且在网格尺寸不大于50.00 mm×50.00 mm时,许用应力为[σ] =1.6×235.0/K,许用等效应力[σV]=300.8 MPa。
根据规范要求,主要支承构件由于载荷作用产生的垂向变形应不大于0.005 6lg(lg为主要支承构件的最大跨距)。根据舱口盖横梁跨距1.5 m和纵桁跨距2.2 m,得到规范限制变形值s=8.40 mm。
由于布置参数影响设计变量的数量,因此需要对每种布置参数分别进行优化,最后选出最优方案。以方案五为例,对拉丁方试验的366个样本进行有限元求解,建立样本空间,部分数据如表1所示。
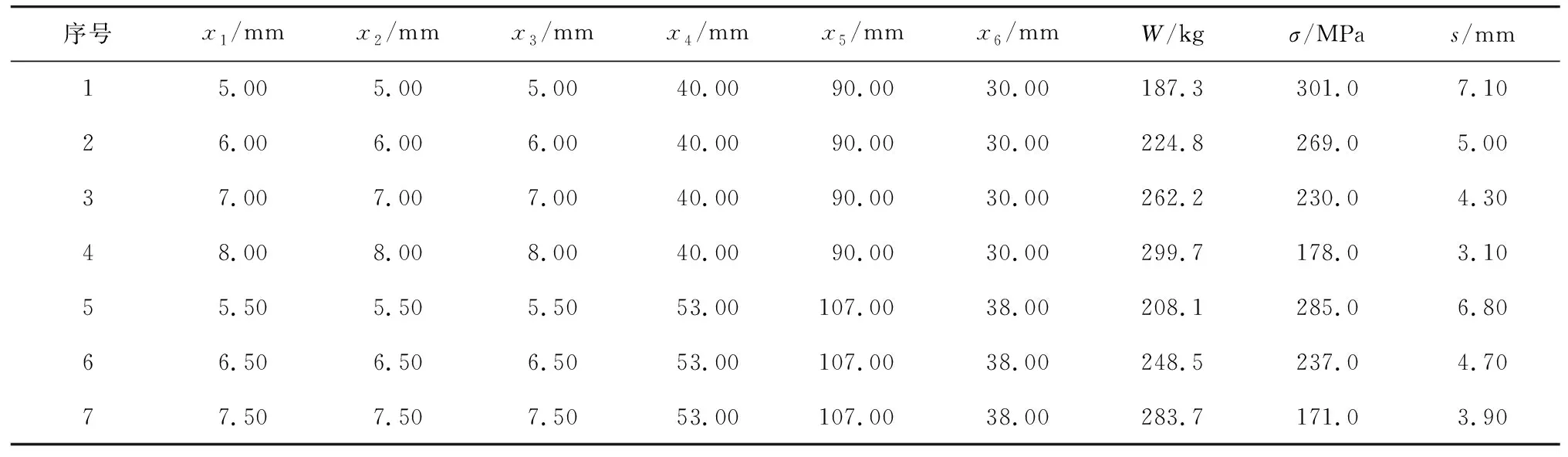
表1 舱口盖结构设计样本的有限元求解数据(部分)
3.2 基于近似模型的结构优化
以方案五为例,根据样本数据的有限元计算结果,采用响应面法建立近似模型,得到目标函数(舱口盖结构质量)、最大应力、最大变形与设计参数的关系为
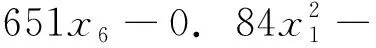
(3)
Stress=219.25-68.14x1+0.204 83x2-0.119 63x3-45.1x4-0.505 37x5+0.060 651x6-
(4)
Deformation=5.34-1.98x1+0.204 83x2-0.119 63x3+1.14x4-0.505 37x5+0.060 651x6+
(5)
式(3)~式(5)中:Weight为舱口盖结构质量;Stress为最大应力;Deformation为最大变形;x1~x11为设计参数。
一般用复相关系数对近似模型的精度进行评估,评估公式为
(6)
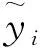
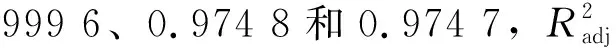
在响应面模型的基础上,采用多岛遗传算法进行结构优化,经历15 186次迭代,优化目标的迭代过程如图6所示。尽管迭代次数较多,但由于采用响应面模型,总体计算工作量并不是很大,整个优化过程历时642 s。
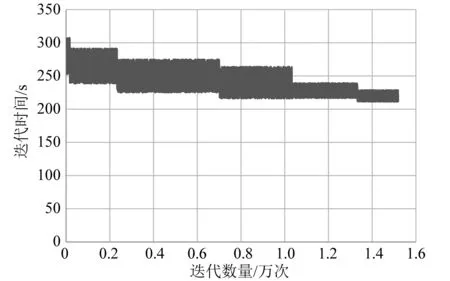
图6 舱口盖质量迭代曲线
比较9种方案的最优解,得到最终优化解,如表2所示。最终优化解的舱口盖质量为216.7 kg,比原设计方案降低6.03%。

表2 优化的舱口盖结构设计参数
3.3 优化解验证
根据优化的参数进行舱口盖结构有限元分析。舱口盖结构等效应力如图7所示。由图7可知:最大等效应力σe=269.5 MPa,发生在长度方向的锁紧装置处。许用等效应力[σe]=300.8 MPa。最大变形为4.99 mm,小于规范限制变形值。因此,构件不会发生失效。

图7 舱口盖结构等效应力
4 结 语
以某船舱口盖结构优化设计问题为例,采用响应面法建立设计变量与目标函数和主要约束的近似模型,通过仿真试验证明近似模型的精度和优化计算可降低计算复杂度。基于近似模型,采用多岛遗传算法,实现对某船舱口盖结构的优化设计,并得到符合设计要求的最优解,比原设计方案降低6.03%的质量。

