顾及地形复杂度因子权重的多波束点云抽稀算法
2
(1.山东科技大学 测绘与空间信息学院,山东 青岛 266590; 2.自然资源部 海洋测绘重点实验室,山东 青岛 266590)
海底地形测量是海洋测绘的基础性任务,其获取的海底地形地貌信息是支撑海洋开发活动的基本资料[1]。多波束测深系统以宽覆盖、高精度的优势,大幅提高了海底地形的测量效率和质量,已成为水深测量任务中首选的探测设备[2]。由于多波束点云数据具有海量性的特点,大量冗余的水深点在参与地形分析运算时会造成时间和硬件资源的浪费,为海底地形数据的管理、存储与成图工作带来运算压力。因此,进行多波束点云数据的简化研究具有重要的现实意义。
目前常用的点云抽稀算法大致可以归纳为不顾及地形特征和顾及地形特征两类。不顾及地形特征的算法主要包括基于规则格网的抽稀和基于系统规则的抽稀[3],基本原理是依据一定的随机采样规则进行数据简化。此类算法侧重于提升运算效率而忽略了地形特征,地形精度损失较大,容易导致局部细节的丢失。许多学者提出了多种顾及地形特征的算法,如基于不规则三角网(triangulated irregular network,TIN)的抽稀算法[4],通过计算局部所有三角形的法向量,根据最大与最小法向量的夹角大小进行数据点取舍。也有学者将地形特征因子与TIN结合,如基于TIN与坡度的算法[5]通过比较某点关联三角面的最大坡度差与设定阈值的大小进行抽稀,其阈值判断标准还可以是高差[6]、曲率[7]等地形特征因子。基于坡度熵的抽稀[8]在此基础上引入熵理论,将局部区域的坡度熵作为表征地形丰富和变化程度的指标。但是,仅采用单一特征参数进行地形变化的分析较为片面,阈值选定对于抽稀质量的影响较大,并且在一些特殊地形点会判断错误[9]。基于多元地形特征的抽稀[10]利用主成分分析与多因子理论,提取几类贡献度较大的特征因子来描述地形复杂度,抽稀质量相对于采用单一地形因子算法有所改善,但复杂度经验公式存在优化空间,地形精度仍有待提高。
因此,提出一种顾及地形复杂度因子权重的多波束点云数据抽稀算法,本算法基于点云构建的不规则三角网结构提取局部地形起伏度、坡度和粗糙度因子,引入改进CRITIC(criteria importance though intercrieria correlation)法确定三者权重,从而构建一种地形复杂度指标作为抽稀判定标准,并将局部最深最浅点、边界点视为特征点予以保留。通过对比实验表明,本算法的抽稀结果在精度上优于传统简化算法,提升了地形表达的真实性和完整性。
1 地形复杂度指标构建
为了减小数据压缩过程中的地形精度损失,点云取舍标准的确定至关重要。本研究将地形复杂度指标作为抽稀依据,首先考虑提取多个地形特征因子,以克服单一参数量化的局限性;然后遵循独立、有效、易于计算[11]的原则筛选所需因子,保证复杂度指标的构建可行性与表达准确性;最后融合地形因子,关键在于权重系数的分配,本研究引入CRITIC多因子综合评价法,以获得最优定权结果。
1.1 地形因子筛选
地形复杂度是反映整体或局部地球表面起伏和褶皱程度的一类指标,可用地形特征因子表征,常见因子包括坡度、坡向、地表曲率、高程标准差、地形起伏度、地形粗糙度、地形分形维数[11]等。在筛选时,可以遵循相对独立性、因子有效性、易于局部计算三个原则。其中,局部地形的起伏程度受极值影响较大,地形起伏度代表局部最大高程与最小高程之差,无均值参与运算,能够有效反映地形变化;基于地形坡面特征计算出的坡度、坡向存在较大相关性,坡向多用于气象、生态领域研究,而坡度用来表征地表曲面的倾斜程度,被认为是最重要且有效的地形因子;地表曲率、地形粗糙度可对地形曲面特征进行有效描述,而TIN结构中曲率一类的参数难以计算,因此不宜选择。综上考虑,本研究选用地形起伏度、地形坡度、地形粗糙度作为构建地形复杂度指标的三个评价因子。
地形起伏度是定量描述地表形态的重要指标,等于区域内的最大高差,具体算式为:
R=Hmax-Hmin。
(1)
式中,R代表地形起伏度,Hmax、Hmin分别为TIN结构中某局部中心点与其关联邻近点中的最大、最小高程。
地形坡度等于坡面垂直高度和水平方向距离的比。在TIN结构下,局部区域的坡度可以由中心点关联的每个三角面坡度的均值表示,三角面坡度的定义为:
(2)
式中,nx、ny、nz为标准矢量n三个方向的法向量,标准矢量n是方向向外并垂直于平面的直线。
地形粗糙度又称局部褶皱度,一般由区域实际面积与相应投影面积之比计算得到[12]。由于地表实际面积难以计算,因此在TIN结构中,常用中心点关联的所有三角面面积代表区域实际面积,则地形粗糙度Kr定义为:
(3)
式中,Ss为局部实际面积,S为局部投影面积,cosa由坡度经三角函数转换求得,N为中心点关联的三角面个数。
1.2 地形因子权重分配
确定参与评价的三个地形因子后,各因子的权重分配将极大影响地形复杂度模型的可靠性。赋权方法主要分为主观和客观赋权法,主观赋权法脱离实测数据,而客观赋权法通过数学方法从原始数据中提取指标间的信息,避免主观因素干扰,具有严密的数学理论基础,适用于地形复杂度指标的评价。其中,大多客观赋权法凭借单一标准进行权数确定,如主成分分析法、变异系数法、熵权法等,而CRITIC法同时考虑了评价指标间的对比强度与冲突性,其评价结果相对其他方法更为全面客观[13]。
CRITIC法采用Pearson积矩相关系数描述指标间的冲突性,相关系数越小,冲突性越高,所占权重越大;对比强度反映样本在同一指标下的离散程度,采用标准差σ表示,σ越大,对应权重越大。虽然传统CRITIC法的赋权方式已经较为完善,但一方面使用Pearson系数只限于评价指标之间的线性关系,并不能准确衡量实际相关关系[14],且样本需满足正态分布,数据适用性低;另一方面,三种地形因子的量纲、单位、均值不同,常规采用标准差衡量对比强度失去意义,不再适用。因此,本研究对传统CRITIC法进行两方面改进。
1) 采用距离相关系数(distance correlation)代替Pearson相关系数进行衡量冲突性的改进。距离相关系数是一种新的度量指标相关性的方法,其优势在于能够实际描述指标间的任意相关关系[15],且无需满足任何模型假设和参数要求。
距离相关系数基于距离协方差dCov(u,w)和距离方差dCov(u,u)dCov(w,w)计算,则指标u与指标w之间的距离相关系数定义为:
(4)
式中,dCov2(u,w)=S1+S2-2S3,S1、S2、S3的计算公式分别为:
(5)
(6)
(7)
同理可计算dCov(u,u)和dCov(w,w)。
同时,为提高针对海量多波束点云的计算效率,可采用快速算法[16]计算该系数。

(8)
则基于改进CRITIC法构建地形复杂度指标的步骤如下。
i. 根据式(4)与式(8)计算出各地形因子的距离相关系数dCorr和变异系数v;
ii. 根据CRITIC赋权法的基本思想,构造融合对比强度与冲突性的综合系数
(9)
式中,k为地形因子个数,dCorrij为第i个与第j个地形因子间的距离相关系数,vj为第j个地形因子的变异系数,Cj越大表示第j个地形因子对地形复杂度的贡献越大,应赋予更大的权重。
iii. 求取各地形因子的归一化权重
(10)
iv. 构建地形复杂度指标时,由于变异系数消除了各地形因子的量纲影响,为了表示地形因子原始值与复杂度指标的关系,需要进行反无量纲化处理,从而得到地形复杂度指标T与各地形因子原始值的关系式:
(11)

2 点云抽稀
点云抽稀的主要目的是降低数据冗余,但实现这一前提需要尽可能保证简化后的数据质量,最大程度保持原始地形特征与细节,从而便于快速构建高精度的海底数字高程模型(digital elevation model),提高海底地形可视化效果。另外,针对多波束测深数据的特性,在抽稀过程中需要考虑保留部分特征点以兼顾航行安全与海图生产业务的需求。因此,本研究首先根据地形复杂度进行初步抽稀,然后对局部最深与最浅点[3]、边界点[17]予以保留,实现多波束数据的高保真抽稀,使结果数据满足上述实际应用要求。
2.1 基于地形复杂度抽稀
将1.2节构建的地形复杂度指标T作为点云取舍的主要判断准则,依次求取所有水深点的地形复杂度T,由于T值代表该点所在局部区域的地形起伏和褶皱程度,因此按T值大小对所有水深点进行排列,抽稀时根据实际需要设置合适的阈值,优先剔除T值较小的冗余点,从而保留并输出对地形变化贡献较大的水深点,实现考虑地形特征的水深点初步简化。
2.2 特征点保留
在水深点简化过程中,一些对地形变化贡献度不大的点会被剔除掉,而此类数据对构建真实海底地形模型、满足海图制图条件以及后续数据分析都具有一定作用。结合多波束水深数据的特点,将局部范围内的最深与最浅点、测区边界点视为两类特征点,并进行提取和保留。
1) 设计一种用来保留局部范围内最深点与最浅点的自适应格网分区算法,具体步骤为:
i. 根据式(12),由总点云数量p动态计算二维网格行列数q,然后遍历所有点云坐标数据求出X、Y方向最大与最小坐标值(xmax、xmin、ymax、ymin)。
(12)
式中,a为计算保留点个数的经验系数,本研究取值0.02。
ii. 依据式(13)求出网格单元分别在X、Y方向的坐标间隔,并建立q×q大小的矩形区域;
(13)
iii. 遍历所有点云的坐标,按照其位置索引存入所在网格单元内;
iv. 遍历所有网格单元,当网格单元至少存在两组数据时,保留网格内的最深与最浅点,若网格单元只包含一组水深点数据则直接保留,其余水深点删除。

图1 提取边界点示意图Fig. 1 Diagram of extracting boundary points

图2 抽稀算法具体流程Fig. 2 Specific flow of thinning algorithm
该算法视测区数据量与点云分布情况不同,对原始测深点云进行自适应格网划分,从而将需要保留的最深、最浅点数量控制在合理范围内,有助于补充完善整体区域的细节特征,同时避免了大面积数据缺失的情况,兼顾了多波束抽稀的地形完善性准则[3]。
2) 采用Alpha-shapes算法提取整体区域的边界点(图1)。在离散水深点集内,设置一个判别半径r,过任意两点绘制半径为r的滚动圆,判断此圆内部是否存在其他点云,若不存在,则认为这两个点是边界点。
统计提取的两类地形特征点,将特征点集与2.1节计算的初步简化点集合并,并剔除重复点,输出最终抽稀结果。
2.3 算法流程
图2展示了改进算法的流程,可概括为以下七个主要步骤:
1) 利用离散点云数据构建TIN结构,获得水深点与邻近关联点的空间关系;
2) 遍历所有水深点,提取各点的三种地形因子信息;
3) 基于改进CRITIC法构造地形复杂度指标作为点云取舍的判定准则;
4) 计算各点地形复杂度,保留复杂度大于特定简化率下的阈值的点,实现数据初步简化;
5) 通过自适应格网分区,保留局部范围内最深点与最浅点;
6) 提取原始点云数据的边界点,与步骤5)结果合并为特征点集;
7) 将步骤4)、6)的结果数据合并,输出所有保留的水深点。
3 实验与分析
选择由多波束系统获取的真实海底点云作为实验数据,将本算法和其他传统算法的抽稀结果对比分析,验证提出算法的可行性和适用性。
3.1 实验区域概述
实验选取的海底地形数据采用R2Sonic-2024型号的多波束测深系统采集,于2017年4月完成外业测量,测区位于中国舟山群岛东南部附近海域,实验选取地形变化较为明显的两个局部区域作为研究对象(图3)。其中,截取的区域1地形起伏相对较大,区域2地形较为粗糙,二者的基本信息如表1所示。实验所用数据均为经过原始数据解析、预处理的点云结果数据。

图3 实验区域示意图Fig. 3 Schematic illustration of the experimental area

表1 实验点云数据基本信息表Tab. 1 Basic information of experimental point cloud data
3.2 实验结果分析
利用本算法构建两个实验区域的地形复杂度模型,得到两个区域的地形复杂度指标T与各地形因子原始值之间的关系分别为:
T1=0.548 9×R+6.016 2×S+0.018 5×Kr,
(14)
T2=0.578 9×R+2.394 5×S+0.040 5×Kr。
(15)
为检验本算法的抽稀效果,实验设置五档简化率(被剔除的点云数目与点云总数目的比值)代表不同的点云简化程度,选取未改进算法、基于坡度[5]和基于高差[6]算法进行对比。其中,未改进算法与本算法的区别在于采用传统CRITIC法构建地形复杂度指标。
首先,采用检查点法的思想对抽稀结果进行精度评定,即按照随机原则均匀抽取部分原始数据作为检查点,将这些点位在TIN结构下的线性内插值与实际水深值逐一作差得到误差,并统计所有点位的均方根误差(root mean square error,RMSE),RMSE值越小说明精度越高。两个实验区域均随机抽取了原始数据的2%作为检查点,实验结果如表2、表3所示,图4可以直观地反映出各算法在不同简化率条件下的精度变化情况。
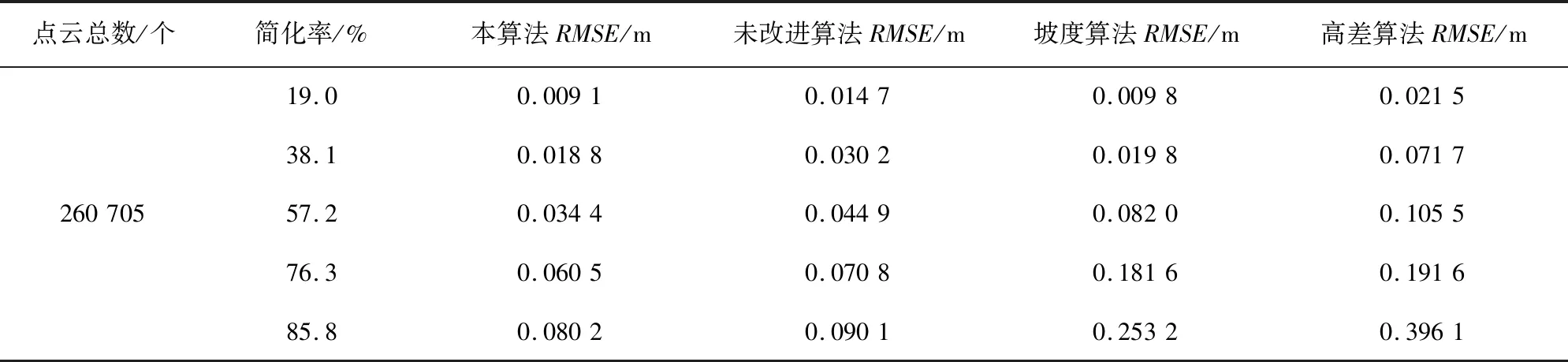
表2 区域1抽稀结果误差统计Tab. 2 Error statistics of thinning results in area 1

表3 区域2抽稀结果误差统计Tab. 3 Error statistics of thinning results in area 2
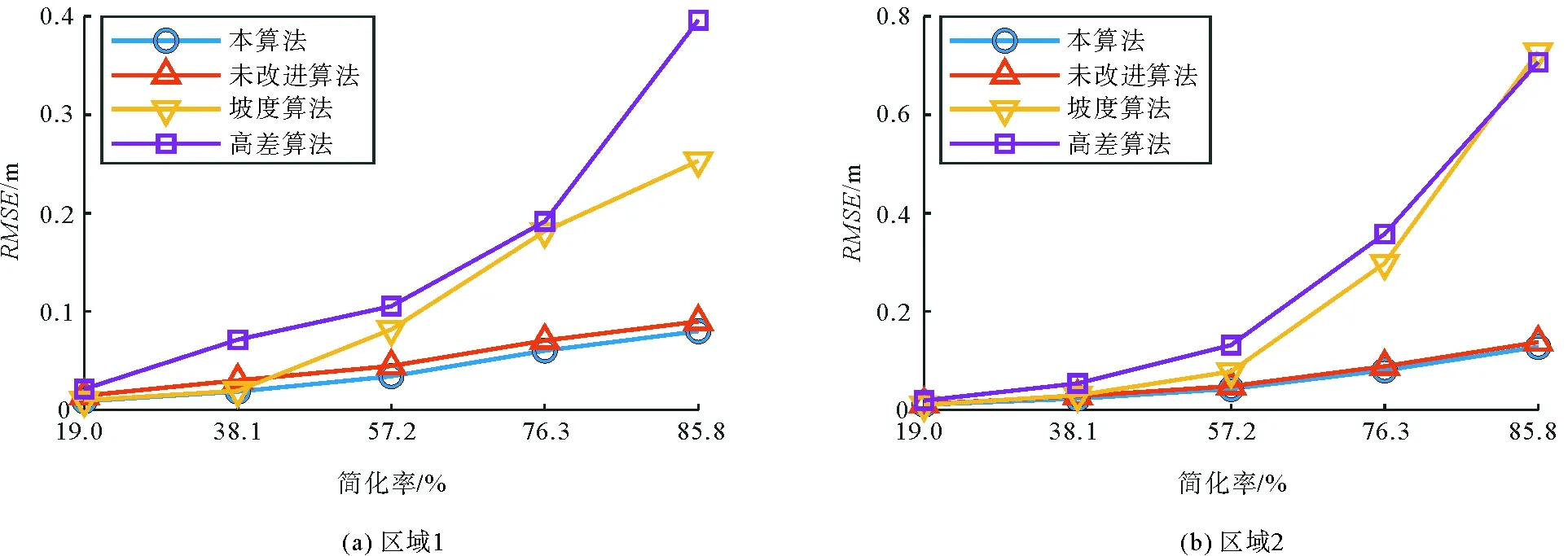
图4 不同算法精度对比Fig. 4 Accuracy comparison of different methods
比较表2、表3精度评定数据发现,针对两个实验区域,各算法的抽稀结果在整体趋势上,随着简化率的增大,RMSE值逐渐增大,点云质量与简化程度呈负相关关系;在所有简化率条件下,本算法相比未改进算法的RMSE值均有所减小,点云抽稀质量更好;在简化率最小(简化率=19.0%),即简化程度最低时,本算法与坡度算法在两个实验区域下的RMSE数值大小非常接近,抽稀质量基本相当,而高差算法的误差相对较大,在其他四档简化率条件下,本算法的RMSE值均为最小,特别是简化率达到70%以上时,抽稀质量相比高差算法与坡度算法具有显著优越性;进一步分析误差曲线(图4),随着简化率增大,本算法的误差值上升趋势相对高差与坡度算法较为平缓。
其次,从主观视觉角度观察和分析本算法在地形真实性表达上的优劣。本研究以简化率76.3%条件下的抽稀结果为例,基于Surfer软件对框选区域i、ii、iii、iv(图5(a)、图6(a))的点云进行插值生成1 m×1 m格网数据,并渲染得到局部地形晕渲图(图5(b)、图6(b)),可以发现,在局部区域ii、iii、iv内,基于高差抽稀的地形图表现出较为严重的失真现象,坡度算法的抽稀结果在局部区域i、iii中也出现一定程度的异常。此外,对于其他局部区域,坡度与高差算法的地表较为光滑,部分地形特征的表达不明显甚至消失,这是由于二者仅采用单一抽稀判定标准,部分对地形变化贡献大的点被误删,且未能全面考虑特征点的影响,其抽稀结果存在局部点云缺失的情况,致使生成的格网模型与实际地形不符;未改进算法的整体表达较好,但对于部分特征的呈现相较本算法仍有所欠缺。综上,本算法的图像能够更好地描述细节特征,在保持原始地表形态方面优于其他算法。

图5 区域1实验结果晕渲图Fig. 5 Hill shading of area 1 experimental results

图6 区域2实验结果晕渲图Fig. 6 Hill shading of area 2 experimental results
4 结论
点云抽稀是多波束测深数据处理的重要环节之一,为了提高点云简化质量,以满足后续地形表达与处理的需要,提出一种顾及地形复杂度因子权重的多波束点云抽稀算法。实验分析表明,本研究通过综合评价法对多个因子进行综合分析,构建的地形复杂度指标能够很好地匹配地形特征,相比采用单一地形因子,该算法的点云取舍标准更为合理。此外,算法考虑局部最深最浅点与边界点的影响,确保了点云数据的整体性,并在一定程度上起到完善地形细节的作用。本算法在降低数据冗余的同时,相较传统算法提高了地形精度,其结果在保持地形真实性上具有优越性,且算法在不同地形都表现出良好的适用性。

