基于DMFF-Net的地震随机噪声压制新技术

钟铁， 陈云， 卢绍平， 董新桐， 李月， 杨宝俊

1 现代电力系统仿真控制与绿色电能新技术教育部重点实验室， 吉林 132012 2 东北电力大学通信工程系， 吉林 132012 3 中山大学地球科学与工程学院， 广州 510275 4 南方海洋科学与工程广东省实验室， 广东珠海 519000 5 吉林大学仪器科学与电气工程学院， 长春 130026 6 吉林大学通信工程学院， 长春 130012 7 吉林大学地球探测与信息技术学院， 长春 130026

0 引言

随机噪声是地震勘探中的一种常见噪声干扰，主要包括风成噪声、人文环境噪声以及检波器与接收面耦合不良引起的噪声等(李光辉和李月, 2016; Dong et al., 2019b，2020).随机噪声在地震记录中通常是“杂乱无章”的，并表现为非平稳、非高斯、与有效信号存在频谱混叠等一系列复杂特征(Zhong et al., 2015)，影响地震资料整体质量与信噪比，且噪声压制难度较大(Yilmaz, 2001).此外，随着易探易采资源的逐渐枯竭，需要对深层、薄层以及不规则地震中的非常规油气进行开发利用，这对地震资料的质量提出了更高的要求.因此，如何有效压制随机噪声并完整恢复有效信号成为了勘探工业亟待解决的关键技术之一.

针对地震资料随机噪声抑制问题，国内外学者进行了大量研究工作，提出的消噪方法大致可分为以下四类：第一类是经典消噪方法，主要包括中值滤波(刘洋等, 2008)、维纳滤波(Mendel, 1977)和F-X预测滤波(Bonar and Sacchi, 2013；石战战等, 2022)等数理方法.这类方法主要是利用有效信号和噪声在时域物理特性以及频率特征方面的差异，实现信号提取和噪声压制.但是上述方法普遍对噪声平稳性有先验要求，同时面对复杂非平稳噪声时处理效果不佳(Zhong et al., 2021).第二类是时频域滤波方法，主要包括带通滤波、短时傅里叶变换(Liu et al., 2017)、时频峰值滤波(林红波等, 2011)等方法.时频域滤波方法主要通过分析信号时频特征，确定信号区域并选择适合的滤波阈值，实现有效信号精细恢复和噪声可靠压制.然而，由于时频域滤波方法难以实现混叠状态下信号和噪声的有效分离，在处理实际勘探资料时，无法有效恢复受到低频混叠随机噪声影响的有效信号(董新桐等, 2021).第三类是基于多尺度分解的滤波方法，主要包括小波变换(Wavelet Transform, WT)(Mousavi et al., 2016)、曲波变换(袁艳华等, 2013)、shearlet变换(董新桐等, 2019)和seislet变换(Fomel and Liu, 2010)等.这类方法可以对分析信息进行稀疏分解，并对不同尺度信息设置合理阈值门限，实现噪声有效抑制.但是上述方法的去噪结果严重依赖阈值函数的选取，面对复杂勘探记录时，往往难以获得最优阈值参数，可能导致相关方法去噪能力退化(Dong et al., 2020).第四类是基于扩散滤波思想的消噪方法，例如自适应分型守恒滤波(Zhong et al., 2021)、各向异性扩散滤波(Baddari et al., 2011)、自适应变分各向异性扩散滤波(Zhou et al., 2016)等.扩散滤波方法主要通过构建扩散滤波方程，设置滤波参数控制扩散项和反扩散项来平衡噪声压制和信号保持作用，在考虑信号保持情况下实现复杂噪声的最大程度衰减，相关研究表明此类方法对低信噪比记录处理能力有待提升(Bonar and Sacchi, 2012).其他一些代表性噪声衰减方法包括经验模态分解(Empirical Mode Decomposition, EMD)(Bekara and Van Der Baan, 2009; 颜中辉等，2017)、奇异值分解(Singular Value Decomposition, SVD)(桑雨等, 2014；马小军和吴庆举, 2020; 姜占东等, 2021)、字典学习(Chen et al., 2016；张良等, 2019；贺月等, 2021)等方法，虽然取得了一定的应用，但是面对复杂勘探噪声时，处理结果仍难以令人满意.

近年来，卷积神经网络作为一种高性能有监督的深度学习方法(Zhu et al., 2019; 吕尧等, 2020)，已经在图像去噪、特征学习、图像分类、物体检测等很多领域取得成功应用(王钰清等, 2019；孙小东等, 2020).一些经典去噪网络框架，例如前馈去噪卷积神经网络(Feed-Forward Denoising Convolutional Neural Networks, DnCNN)(Zhang et al., 2017; Zhao et al., 2019；高好天等, 2021)和U-Net(Ronneberger et al., 2015; Sun et al., 2020)已经被引入到地震勘探资料随机噪声削减领域.针对低频混叠随机噪声削减问题，本文提出了一种双层多尺度特征融合去噪网络(Double-layer Multi-scale Feature Fusion Denoising Network, DMFF-Net).具体来说，DMFF-Net采用双层并行网络结构，上层为原始DnCNN网络，下层为改进DnCNN网络.改进DnCNN网络主要通过引入多分支模块(Diverse Branch Block，DBB)替代传统卷积操作，实现不同尺度、不同复杂度分支的信息融合，提升网络特征的表达能力；此外，利用空洞卷积来扩大感受野，进而有效减小参数数量和计算复杂度.在此基础上，利用跳跃连接操作将浅层信息与深层信息进行融合，提高浅层信息利用效率，保证弱信号处理能力和网络恢复信息的鲁棒性.同时，结合正演建模数据和实际勘探噪声资料构建了信号训练集和噪声训练集，保证了去噪网络训练效率.模拟和实际数据实验结果均表明，本文提出方法可以有效提升勘探记录信噪比，并能够从复杂勘探资料中完整恢复出有效反射信息.

1 DMFF-Net去噪原理

1.1 DnCNN网络结构

DnCNN是由Zhang等(2017)提出的一种去噪网络.如图1所示，DnCNN主要由卷积层Conv、批标准化层BN和激活函数ReLU组成.具体来说，DnCNN首先使用一个由3×3的卷积核和ReLU函数组成的卷积块实现对处理记录特征的初步提取.在此基础上，引入BN模块对输入数据进行标准化处理，并结合卷积层和激活函数构建新的卷积块，实现对数据高维特征的分析获取，最后通过一个1×1的卷积模块对全局信息进行整合.这里，卷积层主要通过卷积运算提取数据隐含特征，如公式(1)所示：

c=ω*a+b,

(1)

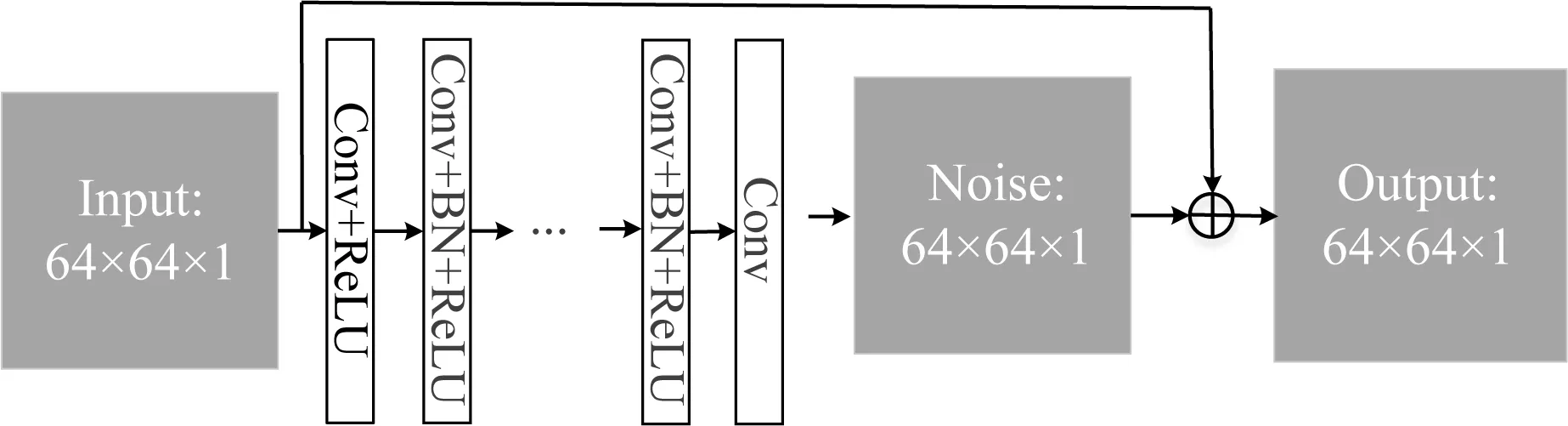
图1 DnCNN网络结构Fig.1 The architecture of DnCNN

其中，a和c分别为卷积层的输入和输出，ω和b为权重和偏置.BN主要对给定模块输入进行归一化处理，使其满足均值为0方差为1，提升网络收敛速度和性能，具体过程如公式(2)所示：

(2)

其中，B代表批标准化尺寸；p和q分别代表BN的输入和输出；η表示一个极小的常数；γ和β表示可学习的参数.此外，激活函数ReLU是一种非线性函数，可以通过公式(3)表示：

f(x)=max(0,τ)，

(3)

其中，τ表示激活函数的输入.在实际地震资料处理过程中，DnCNN网络结构相对单一，随着深度增加，浅层信息得不到有效利用.在面对低信噪比记录时，处理结果可能发生退化(董新桐等，2021).

1.2 DMFF-Net网络结构

为进一步提升地震资料处理能力，本文提出了一种DMFF-Net消噪网络，其基本结构如图2所示.

具体来说，DMFF-Net采用双层的网络结构，通过增加网络的宽度来提高网络的性能.其中，上层网络采用原始DnCNN结构，用于提取特征；下层网络为结合空洞卷积和DBB模块的改进DnCNN结构，用以丰富特征空间并提升特征提取能力.网络中使用的空洞卷积是一种改进的卷积结构，它是通过在卷积核中填充0，从而改变卷积核的大小.具体来说，空洞数为r的空洞卷积实际上就是在卷积核中添加r-1个0.通常空洞卷积可以有效扩大网络感受野，并提取分析数据的多尺度的信息.本文采用空洞数为2的3×3卷积核，其感受野与传统5×5卷积核相当，即在保证分析精度的前提下有效减小了网络的参数数量.同时，针对传统卷积模块提取特征单一问题，本文提出利用DBB模块替代传统卷积模块，实现对输入数据的多尺度分析.DBB模块的结构如图3所示，其利用多尺度卷积和平均池化操作来增强单个卷积的表示能力，得到不同尺度的特征，最后进行融合，可以有效提升训练模型的性能水平.在此基础上，构建跳跃连接操作，利用Cat模块将原始输入与深层提取的特征进行融合，挖掘出更加精细的潜在特征，进一步增强去噪网络的表达能力.最后，对子网络特征按通道进行拼接融合，提取输入数据更为全面的特征，切实提升压制噪声水平.

图2 DMFF-Net网络结构Fig.2 The architecture of DMFF-Net

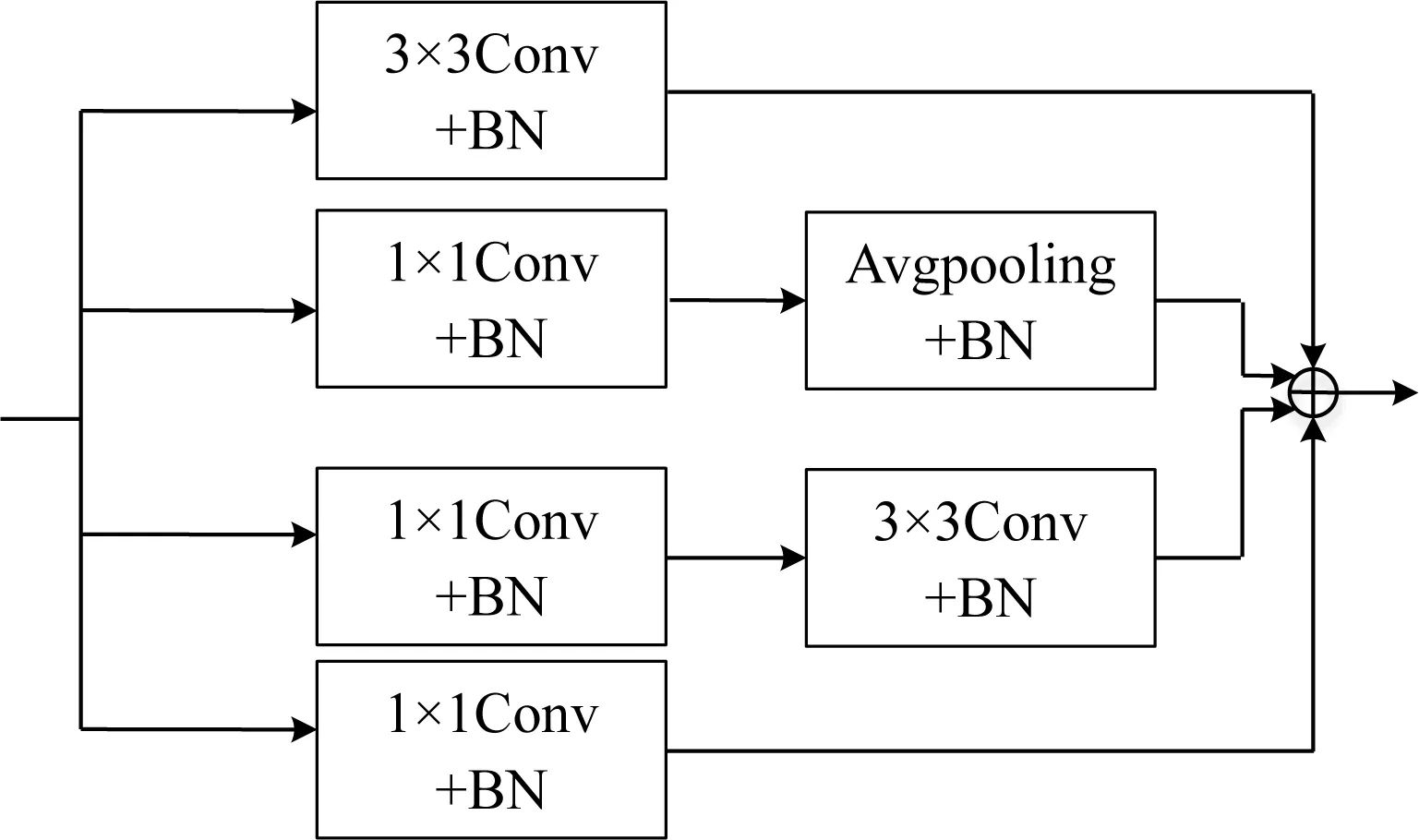
图3 多分支模块结构Fig.3 The architecture of diverse branch block

1.3 去噪原理及详细流程

通常，实际勘探数据可以看作是纯净信号与加性噪声的叠加结果，如公式(4)所示：

y=x+n，

(4)

其中，x代表纯净信号数据，n代表叠加的噪声，y代表含噪数据.通过残差学习思想，可以构建含噪数据y与叠加的噪声n之间的非线性的映射关系，如公式(5)所示：

(5)

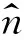
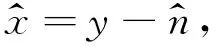
(6)

这里，利用公式(7)所示的损失函数实现网络参数的优化：

(7)

式中，ni=yi-xi表示噪声训练数据，‖LDMFFNet(Θ)‖F为Frobenious范数.通过优化损失函数，可以调节网络参数，实现最优映射关系的获取.

2 网络训练及参数选取

2.1 训练集的构建

训练集的完备性影响着有监督深度学习网络的学习效果和去噪结果准确性.DMFF-Net的训练集由信号集和噪声集组成，利用大量高真实性训练数据满足网络训练及参数优化要求.对于信号集而言，由于无法从实际地震记录中提取纯净信号，本文采用正演建模的方式构建信号训练集.具体来说，利用不同主频率的雷克子波、零相位小波和混合相位小波来模拟地震记录中的有效信号，建模公式如下：

雷克子波：

f(t)=A[1-2×(πf0(t-t0)2)]×e-(πf0(t-t0))2，

(8)

零相位子波：

(9)

混合相位子波：

(10)

其中，A表示振幅，t0表示初始时间，f0表示主频，r1和r2分别用于调整零相位子波和混合相位子波的波形，具体建模参数如表1所示.通过正演建模方法获得100幅模拟地震记录，利用64×64的滑动窗函数对模拟记录进行截取，随机抽选得到8500个信号片，对信号片进行幅值归一化后便得到信号训练集.

表1 正演建模参数Table 1 Forward modeling parameters

为了保证训练模型的消噪精度，利用先期从塔里木盆地测得的2000道(每道30000点)无人工震源激发情况下获得的背景噪声记录来构建噪声训练集.类似地，利用64×64的滑动窗函数对噪声记录进行截取，幅值归一化后得到8750个噪声片，组构得到噪声训练集.为保证网络的泛化性能，将信号片与噪声片随机匹配，保证训练样本的多样性.同时，为了贴近实际记录性质，将匹配的信号片和噪声片叠加获得不同信噪比的含噪数据，含噪数据信噪比范围在-10～0 dB范围内随机选取.典型信号片和噪声片数据如图4所示.

2.2 实验平台及网络参数的选取

为了满足去噪算法的计算需求，搭建实验平台用于网络的训练和测试.实验服务器配置为E5-2600 v4处理器、Windows 10(64位)操作系统、64GB内存、双NVIDA GeForce GTX 1080显卡，利用Matlab2016实现去噪网络的编译.针对网络训练模型，设置训练片大小为64×64，批大小为64，网络的初始学习率设置为[10-3, 10-4]，训练周期设置为50.两个网络并行学习，整体来看网络共有36层，利用Adam算法实现损失函数优化(表2).

本文采用信噪比(Signal-to-Noise Ratio，SNR)和均方误差(Mean Square Error，MSE)来衡量网络的去噪能力，其定义式如下所示(Dong et al., 2019a)：

表2 网络结构参数Table 2 Network structure parameters

(11)

(12)

其中，X表示纯净信号，Y′表示处理后的结果，M和N分别表示道数和采样点数.一般来说，SNR可以衡量去噪方法的消噪能力，MSE可以反映去噪方法的信号保持能力.

3 地震记录处理与分析

3.1 模拟数据去噪结果对比

为了验证DMFF-Net网络压制噪声的性能，利用正演建模方法生成模拟纯净地震记录，如图5a所示.该模拟纯净地震记录共有128道，每道由1024个采样点组成，采样频率为500 Hz.为模拟实际勘探资料特征，利用不同速度模型构建具有不同几何特征的同相轴，同时生成包含断轴在内的复杂同相轴，用以客观验证消噪网络的性能.图5b为塔里木盆地获取的实际噪声记录.观察可知，该记录中随机噪声记录的主频较低且无明显相干噪声存在.将模拟纯净地震记录与实际随机噪声记录进行叠加，得到了信噪比为-6 dB的模拟含噪记录，如图5c所示.由于强背景噪声的影响，有效信号特征变得模糊且难于辨识.利用DMFF-Net网络对模拟含噪记录中噪声进行压制，恢复信号和滤除噪声的结果分别如图5d和图5e所示.结果表明，DMFF-Net可有效压制随机噪声，背景干净，恢复的同相轴信息清晰且连续，与模拟纯净地震记录极为相似；滤除噪声与叠加噪声也具有极其相近的波动特征，且滤除噪声中并无明显的信号残留，验证了本文提出方法在复杂噪声抑制和信号保幅性方面的处理能力.同时，恢复信号信噪比可达到13.76 dB，这也证明了本文所提出去噪网络的有效性.

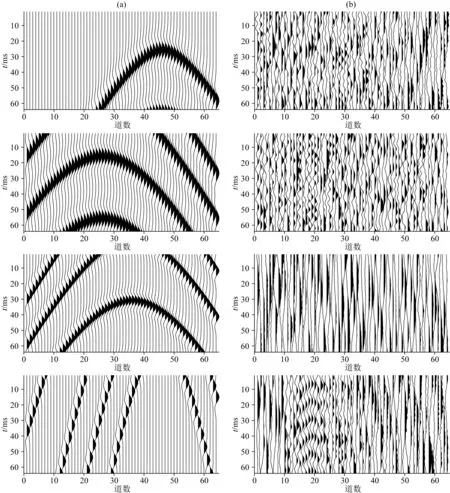
图4 信号训练集和噪声训练集数据示例(a) 典型信号片数据； (b) 典型噪声片数据.Fig.4 Examples of signal and noise training data set(a) Signal data set samples; (b) Noise data set samples.

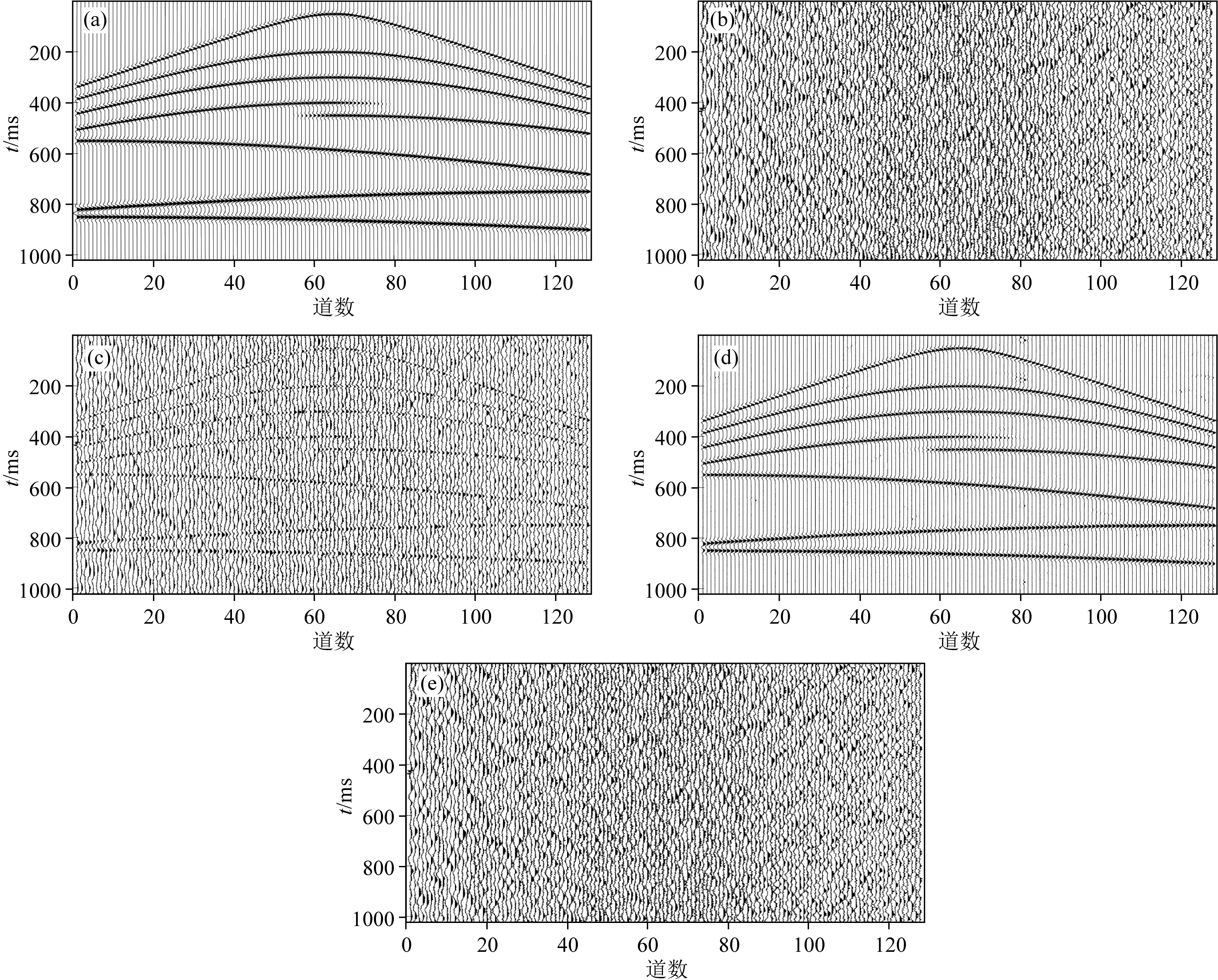
图5 模拟数据去噪结果分析(a) 纯净信号记录； (b) 实际噪声数据； (c) 含噪记录； (d) 去噪结果； (e) 滤除噪声.Fig.5 Analysis of synthetic data denoising results(a) Pure signal record; (b) Field noise data; (c) Noisy record; (d) Denoising result; (e) Filtered noise.

此外，本文选用小波变换、带通滤波器以及传统DnCNN等方法同样对图5c所示的模拟含噪记录进行处理，处理结果和滤除噪声如图6所示.这里，小波变换的基函数设置为db4小波，分解层数为15层，利用软阈值函数实现噪声衰减抑制；带通滤波器的通带范围设置为15～40 Hz；传统DnCNN网络为17层网络结构(Zhao et al., 2019)，在同DMFF-Net网络相同的训练集、实验环境和网络参数条件下进行训练和测试.对比分析不同消噪方法的处理结果：小波变换结果(图6b)中绝大部分同相轴无法有效恢复，噪声压制不彻底，依旧严重破坏有效信号的连续性和可辨识性；带通滤波器(图6c)恢复的同相轴相对模糊，噪声残留严重，同时上述两种传统方法滤除的噪声中均有明显的有效信号残留，这说明相关方法无法有效实现信噪分离，同时，在压制噪声的同时，对有效信号也会造成幅度损失.图6d所示为DnCNN的处理结果，处理结果在噪声衰减和信号恢复方面都要明显优于传统方法，恢复的同相轴清晰，背景噪声也能够被很好地抑制，但是处理结果中存在明显假轴和部分噪声残留.同时，滤除的噪声中也存在部分有效信号的残留.与之对比，DMFF-Net去噪结果(图6e)同模拟纯净地震记录具有更为相近的特征，噪声压制的更为彻底且无明显假轴出现，背景更干净，同相轴更加清晰，滤除的噪声中无明显有效信号残留，处理结果的信噪比可达到13.76 dB，也要高于DnCNN的10.36 dB，这说明了本文提出方法在面对复杂噪声时具有更为优秀的处理能力，不仅能够很好的压制噪声，同时还可以保证信号幅度不被破坏.

在此基础上，比较了处理结果在频谱特性方面的差异，如图7所示.如图7a所示的F-K谱结果表明模拟纯净记录(左图)和叠加的随机噪声(右图)在频率上存在明显混叠，小波变换恢复信号的F-K谱(图7b)同纯净信号的F-K谱存在较大差异，滤除噪声的F-K谱图中有效信号能量残留明显，带通滤波器(图7c)只能保留通带内有效信号，同时无法实现同频噪声的压制，这都说明传统方法在面对低频混叠噪声时处理能力有待提升.图7d和图7e分别为DnCNN和DMFF-Net的处理结果，结果中恢复信号与纯净信号具有相近的频率特征，这也说明深度学习方法在面对复杂噪声消减时的高效处理能力.同时DMFF-Net恢复信号的F-K谱较DnCNN结果更加清晰，滤除噪声中无信号能量残留，验证了DMFF-Net具有更好的消噪能力，可实现低频混叠复杂背景噪声下有效信号的高质量恢复.

在此基础上，对不同SNR含噪记录进行处理，并比较不同处理方法在提升SNR和MSE方面的差异，结果如表3所示.观察可知，DMFF-Net与对比方法相比具有更好的消噪性能，可以更为明显地提升处理结果的SNR，并具有最小的MSE，反映了其在保幅能力方面的优势，验证了DMFF-Net在处理复杂勘探噪声衰减问题的有效性.与此同时，DMFF-Net同样可以有效恢复低信噪比记录中的有效信息，以-10 dB含噪记录处理结果为例，DMFF-Net可提升SNR将近20 dB，而传统DnCNN仅能提高17 dB左右，结果表明DMFF-Net可以在恢复信号的同时有效压制实际低频强随机噪声，在去噪能力方面具有明显的优势.

表3 不同方法SNR及MSE分析比较Table 3 The comparisons for SNR and MSE for different attenuation methods

图6 不同算法去噪结果(左图)及滤除噪声(右图)比较(a) 含噪记录及叠加噪声; (b) 小波变换(2.44 dB); (c) 带通滤波器(2.32 dB); (d) DnCNN (10.36 dB); (e) DMFF-Net (13.76 dB).Fig.6 Comparison of denoising results (left subplots) and filtered noise (right subplots) of different algorithms(a) Noisy record and added noise data; (b) WT (2.43 dB); (c) Band-pass filtering (2.32 dB); (d) DnCNN(10.36 dB); (e) DMFF-Net (13.76 dB).

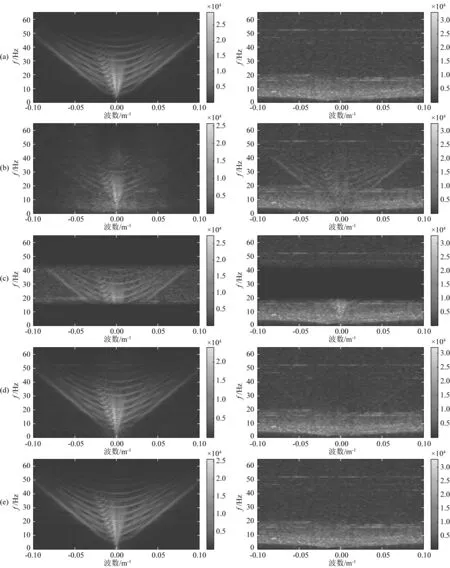
图7 不同方法去噪结果(左图)及滤除噪声(右图)F-K谱对比分析(a) 纯净记录及叠加噪声; (b) 小波变换; (c) 带通滤波器; (d) DnCNN; (e) DMFF-Net.Fig.7 Comparisons for the F-K spectra of denoising results (left subplots) and filtered noise (right subplots)(a) The pure record and added noise data; (b) WT; (c) Band-pass filtering; (d) DnCNN; (e) DMFF-Net.

图8 实际地震数据处理结果比较(左图)及滤除噪声(右图)(a) 实际共炮点记录; (b) 小波变换; (c) 带通滤波器; (d) DnCNN; (e) DMFF-Net.Fig.8 Comparison of denoising results (left subplots) and filtered noise (right subplots) of field seismic data(a) Field common shot records; (b) WT; (c) Band-pass filtering; (d) DnCNN; (e) DMFF-Net.

图9 去噪结果局部放大比较(上图：区域1，下图：区域2)(a) 实际地震资料； (b) 小波变换; (c) 带通滤波器; (d) DnCNN; (e) DMFF-Net.Fig.9 Comparisons of local enlargements (top subplots: results of area 1; bottom subplots: results of area 2)(a) Field seismic records; (b) WT; (c) Band-pass filtering; (d) DnCNN; (e) DMFF-Net.

图10 相近采集环境实际记录处理结果(左图)及滤除噪声(右图)(a) 实际共炮点记录； (b) 小波变换; (c) 带通滤波器; (d) DnCNN; (e) DMFF-Net.Fig.10 Denoising results (left subplots) and filtered noise (right subplots) of the field record acquired in the similar environment(a) Field common shot records; (b) WT; (c) Band-pass filtering; (d) DnCNN; (e) DMFF-Net.

同时，对消噪网络的网络规模、参数数量、训练耗时和处理时间进行了分析，验证消噪网络在实际资料处理方面的可行性.如前所述，研究中使用的DnCNN网络具有17层结构，而为了获取更好的消噪能力，本文提出的DMFF-Net网络具有36层结构.参数数量和训练耗时结果表明：DnCNN和DMFF-Net的参数数量分别为737280和1634304，DnCNN的训练耗时为3.25 h，DMFF-Net的训练耗时为7.21 h.总体来看，DnCNN在计算开销方面较DMFF-Net更具有优势，这也客观的反映了二者在网络结构复杂程度方面的差异.但是，消噪网络具有泛化性，训练后的去噪模型可以用来处理同一测区或性质相近的实际勘探记录，而无需针对每一幅记录重复上述训练过程.从泛化性角度分析，DMFF-Net的训练耗时是可以接受的.此外，就勘探数据处理时间而言，以1024×640的勘探数据为例，DnCNN和DMFF-Net的处理时间分别为0.125 s和0.147 s，明显优于多数经典的时频滤波和变换域分析方法.综上，去噪模型的泛化性和快速的资料处理速度使得DMFF-Net可以应用于海量勘探资料处理实际问题.

3.2 实际勘探数据去噪结果对比

图8a为塔里木地区实际勘测得到的共炮点记录，该记录共216道，每道记录长2.5 s，采样频率为500 Hz.观察可知，实际记录中强随机噪声和面波干扰导致部分区域有效反射信息被湮没，同时同相轴连续性较差，部分同相轴难以辨识.利用小波变换、带通滤波器、DnCNN和DMFF-Net方法对该记录进行处理，结果如图8b—e所示.结果表明，小波变换(图8b)在信号恢复和噪声压制方面处理结果不甚理想，只有部分中高频噪声被滤除，整体去噪结果中仍然有大量低频噪声存在；带通滤波器(图8c)可有效去除面波干扰，但是信号同频噪声无法有效抑制，噪声残留明显.图8d和图8e分别为DnCNN和DMFF-Net处理结果，观察可知较传统方法，噪声得到了更彻底的抑制，同时被面波等强干扰影响的反射同相轴信息也得到了恢复，结果中反射同相轴更加光滑连续.相较而言，DMFF-Net处理结果要优于传统DnCNN网络，以黑色方框圈示区域为例，DMFF-Net可以更加清晰的恢复出浅层同相轴信息，同时恢复的同相轴较DnCNN具有更好的连续性；此外，DnCNN滤除噪声中存在一定的信号泄露，而DMFF-Net结果中无明显的信号残留.

在此基础上，对方框区域进行局部放大，比较结果如图9所示.结果表明，相较传统方法DMFF-Net可以更好的实现信噪分离，面波等强相干干扰也可以得到有效抑制，获得更好的去噪结果；相较DnCNN网络，DMFF-Net恢复的信息更加清晰连续，同时可以重构出一些DnCNN无法有效保留的反射信息，尤其是浅层的细节信息，这都验证了提出方法具有更好的消噪性能和信号恢复能力.

为了验证本文所提出的消噪网络模型的泛化能力，选取了一幅同一测区不同测线接收的地震记录(图10a)进行处理，处理结果如图10所示.图10b和图10c分别为小波变换和带通滤波器的处理结果，结果表明传统方法的处理结果仍然不甚理想，小波变换无法有效压制低频噪声，同相轴依旧被噪声严重破坏，面波等强干扰噪声也无法被有效压制.同时，带通滤波器无法分离同频干扰噪声，有效反射信息恢复不佳.相较而言，DnCNN(图10d)虽然可以有效压制噪声，但是重构的同相轴信息在某些区域略显无序，滤除噪声中也有明显的信号损失；DMFF-Net(图10e)恢复的同相轴更加清晰规律，被面波影响的同相轴信息也得到了较好的恢复，这充分说明DMFF-Net训练得到的去噪模型具有较好的处理精度和泛化性能，能够满足海量地震资料对于通用去噪模型的需求.

4 结论

针对实际勘探记录中低频频带混叠随机噪声压制问题，本文提出了一种双层多尺度特征融合去噪网络：DMFF-Net.该网络是一种针对DnCNN网络的改进方法，通过构建双层网络结构，融合不同网络的预测结果，改善传统DnCNN模型的去噪精度；同时引入DBB模块替代传统卷积操作实现不同分支信息有效融合，提升网络特征学习能力；最后通过跳跃连接操作实现浅层信息和深层信息的融合，进一步提升复杂噪声的压制和微弱信号的恢复能力.在此基础上，将DMFF-Net处理结果同小波变换、带通滤波器和DnCNN网络处理结果进行比较，结果表明DMFF-Net可有效压制复杂低频混叠背景噪声，模拟记录提高信噪比超过20 dB.此外，提出方法也表现出较对比方法更好的信号幅度保持能力，模拟和实际资料处理结果中均没有明显的信号泄露到滤除噪声当中，验证了DMFF-Net方法的有效性.最后，将训练模型应用于相同测区不同测线获得的实际地震勘探记录，结果表明训练模型可实现对不同记录中噪声的有效压制，验证了DMFF-Net去噪模型具有一定的泛化性能，可用于相同类型复杂地震资料的处理.总体而言，本文提出的DMFF-Net网络可实现复杂噪声影响下勘探记录高保真处理，有效压制噪声并准确重构出反射信息.但是，当面对极低信噪比勘探记录时，DMFF-Net的处理能力可能发生退化.同时，如何在保证处理精度和消噪能力的前提下，持续优化网络结构，切实减小计算开销，还需进一步深入研究.尽管如此，DMFF-Net在复杂勘探资料处理领域具有一定的应用前景，也可以为基于深度学习的地震资料处理技术研究提供一定的参考借鉴.