线性规划模型及其应用

郑秋沛

（西藏自治区体育运动技术学校 西藏 拉萨 850000）

模型是揭示某一研究对象的性能和特征而建立的结构，咱们所说的数学模型是一个数学结构而不局限于一个函数关系式，以往数学规划也被称为最优化问题。那么我们为什么要选择建立数学规划模型？因为通过建立模型经常能揭示出许多不明了的关系，建立模型后，人们可以利用数学工具对它进行分析，从而帮助我们提出那些不是显而易见的行动方针。根据决策变量、目标函数和约束条件的不同，数学规划可分为：线性规划、（线性）整数规划、非线性规划、动态规划。[1]本文所探讨的便是这其中的一个分支：线性规划，这是求解最简单的一种规划问题。如果能利用线性规划描述一个规划问题，则说明我们得到了一个简单容易处理的模型结构，而简单容易处理是模型好坏的重要判别依据。

1.简单线性规划在高中教学中的应用

在高中阶段的数学学习中，我们经常会遇到一些光靠笔算推理解决不了的问题，比如在含不等式的函数中的求取值范围的问题，按照一般思路，我们很难求解，如果我们运用简单线性规划构建模型的方法便能轻松解出。因此，我们将高中所学线性规划问题进行归类，这样有助于高中学生更好的学习并使用线性规划。解题策略方面，我们大致可总结出四种结论：（1）利用纵截距（2）利用两点间距离（3）利用斜率（4）利用点线距离。线性规划课程基本按照“画”“作”“求”“答”四个步骤，是以程序化的模式组织起来的逻辑体系。

我们高中所学线性规划问题大致可分为以下几类：

（1）简单线性规划在函数与不等式中的应用

例1 设函数f（x）=ax2+bx,且-1≤f（-1）≤2,2≤f（1）≤4,求f（-2）的取值范围。

分析：在我们没学习线性规划的之前，做这样的题，我们只能先求出a,b的范围，之后才能求出f（-2）的范围，但是，求a,b的范围我们是很容易出错的，而现在我们学习了线性规划知识，那就无需按照老方法计算这样的题。

做出以上不等式组所表示的平面区域，即可行域，并做出平行线族4a-2b=Z，如图。然后再从图中寻找特殊点分别代值，即可求出目标函数的最大值与最小值。

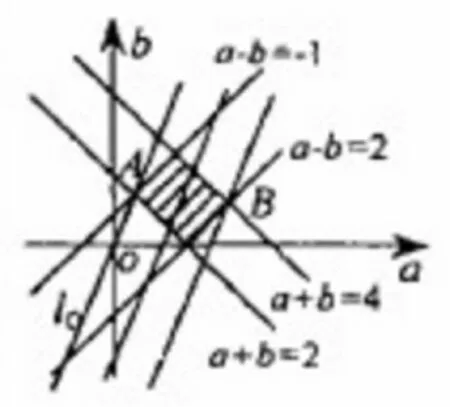
通过上述举例论证，我们可以得出，简单线性规划对解决不等式问题很有效。因为这种方法的习得，大大的方便了我们对高中数学学科中难度问题的研究。虽然线性规划知识在高中数学课程里是一个相对独立的知识系统，但它与直线方程、不等式、函数、圆锥曲线都是有紧密联系的，学生解这一类题需要完美的将线性规划知识和直线方程、不等式等知识相结合，通过老师在课堂上反复的给学生讲解和操练，加强学生对数形结合思想的理解与掌握，学生在理清各种约束条件及目标函数后，通过作图建立可行域，便可将此类问题轻松解出。

（2）简单线性规划在应用性问题中的应用

例24枝郁金香与5枝丁香的价格之和小于22元，而6枝郁金香与3枝丁香的价格之和大于24元，则2枝郁金香和3枝丁香的价格比较的结果是什么？

分析：首先，这道题并不是很难，学习过线性规划知识的同学都能知道，题干中涉及两种花的价格比较，这里可以直接采用设未知数来解决。我们就设郁金香价格为x元，丁香价格为y元，然后直接将两者价格代入题干所给的信息，直接能得到几个不等式，我们将所得不等式建立好模型。

解：设郁金香价格为x元，丁香价格为y元

目标函数为Z=2x-3y

作出一组平行线2x-3y=t（t为参数），该平行线族会经过可行域内的点，此时只需观察t的正负即可。

由于直线4x+5y=22与6x+3y=24的交点为A（3，2）,直线2x-3y=0恰好经过点A，因此经过可行域的点且斜率为2/3的直线在y轴上的截距为负，即从而t＞0,所以目标函数Z=2x-3y的值总是大于0.所以2枝郁金香比3枝丁香贵。

应用型题目这些年来频繁在各地中高考中出现，而调配人力、物力、资金的问题更是屡见不鲜，只能说明现在的中高考出题也越来越贴近生活。这方面也确切说明了解决生活中很多问题也离不开线性规划知识的学习。同样又体现了这一类问题虽然常常是考生觉得棘手的但又是不得不掌握的。不过现在我们学习了线性规划，这类问题还是比较好解决的。

（3）简单线性规划在解析几何中的应用

利用线性规划“同侧同号，异侧异号”的结论，不仅可以求动直线和定线段问题，无需画图，又可避免讨论，而且还可以延伸到解决圆锥曲线中的问题，简洁明快。[2]

由上述可知，线性规划在我们整个高中学习生涯中占了一定的主导地位，学好有关它的知识，对我们将来的学习和发展都十分有利。比如，有些爱好数学的小伙伴大学时填报与数学有关的专业，你有一定的有关线性规划的基础，你在学习运筹学、解析几何、数学建模等课程就比其他人多一点优势；再比如你想学习物理或计算机方面的专业，有时候建立模型也离不开我们之前学的线性规划知识；再比如，一些小伙伴以后想从事与经济、管理等等有关的工作，这也离不开线性规划知识的应用。

2.线性规划模型在生活中的应用

线性规划在生活中的应用就可谓是无孔不入，它不像高中数学只是某几个板块才需要，而是大部分生活问题的解决都需要用到线性规划知识。在实际生活中，我们所得到的约束条件可能就不像笔者在前面所举例的题目中那小小的两个了，所要求解的目标函数可能也不止那么简单了。

首先，线性规划的数学模型的一般形式为：

目标函数：max（min）z=c1x1+c2x2+...+cnxn

满足的约束条件：

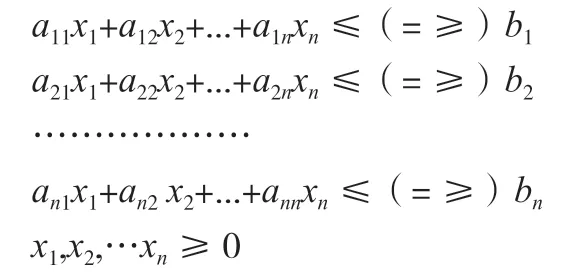
这就和我们之前涉及的只是两个变量两个约束条件完全不是一个档次了。一般来讲，我们所建立的数学模型具有这几个特点：（1）每个模型都有若干个决策变量，且这些变量都是非负的。（2）目标函数是决策变量的线性函数，根据具体问题可以最大或最小化，二者统称为最大化。（3）约束条件是线性函数。

我们将线性规划的知识运用到企业中去，可以使企业适应市场激烈的竞争，并及时、准确、科学的制定生产计划、投资计划、对资源进行合理配置。过去，企业在制定计划、调整分配方面很困难，考虑到诸多因素，企业不可能做什么决定都去进行人工测算，那样真的是耗时耗力又耗资源，先不说在进行人工测算之后所做的决断对企业来说到底是盈利还是亏损，但这前期的投入可能就付诸东流了。[3]再者，人工预算也不能做到灵活机动，若市场稍微出点变动，之前所做的测算可能就得从头再来。但是，如果我们运用线性规划知识并配合计算机建立模型进行测算，就显得主动很多，这种方式简便易行，在短时间内就能拿出最优方案，不仅降低了成本，还提高了企业决策的科学性和可靠性。

将实际生活中的线性规划问题，抽象为数学形式，目的在于找到解决问题的方法。为此，我们作以下一些讨论。

例3：某工厂在计划期内要安排生产Ⅰ、Ⅱ两种产品，已知生产单位产品所需的设备台时及A、B两种原材料的消耗，如表1所示：

ⅠⅡ设备 1 2 8台时原材料A 4 0 16kg原材料B 0 4 12kg

该厂每生产一件产品Ⅰ可获得2元，每生产一件产品Ⅱ可获利3元。问应如何安排计划，使该工厂在限定条件下获利最多？

显见，这个问题可以用以下的数学模型来描述：

设x1,x2分别表示在计划期内产品Ⅰ、Ⅱ的产量，因为设备的有效台时8，这是一个限制产量的条件，所以确定产品Ⅰ、Ⅱ的产量时，要考虑不超过设备的有效台时数，即可用不等式表示为:x1+2x2≤8.同理，因原材料的限量，可以得到两个不等式：4x1≤16,4x2≤12.用z表示利润，这时z=2x1+3x2,综合上述，此计划问题可用数字模型表示为：

数：z=2x1+3x2

根据约束条件作出可行域，找出满足目标函数的最优解便是最大获利。这里只涉及两个变量，因此我们可以不用计算机构建模型。

企业在生产、运输、市场营销等方面，不能很好的利用线性规划进行合理的配置，往往会造成增加企业生产却不能使企业利润达到最大化的局面，还有可能会造成另一种更为严重的局面，就是实践模拟了一大堆之后发现计划落了空，不管是哪一种局面，都会为企业造成不必要的资源浪费。在竞争日益激烈的今天，如果某个企业的管理还按照老办法制定决策时采用人工测验，那么这个企业的发展前景是堪忧的。通过以上一系列举例说明以及陈述，我们便能看出，线性规划不光能解决高中课程中遇到的问题，比如高中数学中的不等式及函数应用，还能解决我们生活中遇到的各种问题，比如求最大利润或最小消耗等问题的最优解。随着线性规划模型的发展，我们已经看到了运用线性规划模型的必要性和重要性。