手机跌落碰撞瞬态动力学分析

李彦，王学军，何文杰

（200082 上海市 上海理工大学 机械工程学院）

0 引言

自由跌落作为电子产品的环境实验的重要项目，传统的实验方式是采用实物进行实验，这并不利于减少电子产品的生产时间和研发周期。将CAE 仿真技术应用到电子产品的设计过程中，能在设计阶段对产品的设计和材料进行检验，检查其是否满足设计要求。

CAE 仿真技术已经在大量的领域内进行广泛的应用，有限元技术也已经成为了工程技术学科最广泛的数值实验手段。有限元方法（Finite Element Method）的核心思想是结构的离散化，将物体的实际结构假想为由互相连接的有限数目的子单元组成，通过对每一个子单元进行分析求近似解，最终推导得到整个域的满足条件的解，从而对问题作出解答。各种CAE 仿真工具已经广泛应用在了航空航天领域。有限元仿真软件具有的多场耦合、非线性仿真，以及与其他设计软件强大的协同工作能力，为解决实际中复杂的工程问题提供了强有力的解决方案[1]。

而在ABAQUS 有限元分析软件中，显式方法（ABAQUS/Explicit）相较于隐式方法（ABAQUS/Standard）所需要的增量步更小。在通常的显式方法模拟中，一般会有10 000-1 000 000 个增量步，这相较于隐式方法，每个增量步需要求解一整套全域的方程，显式方法每个增量步的计算成本更低。虽然最初的显式方法是对于隐式方法的一个补充，然而目前显式方法对于高速动力学事件、更复杂的接触问题、复杂的后屈曲问题、高度非线性的准静态问题，材料退化和失效问题等方面具有较大的优越性[2]。

桥梁、地面移动装置等各类承受各种随时间变化载荷的结构，建筑框架等各类承受各种冲击载荷的结构，手机、笔记本电脑各类承受撞击和颠簸的设备较为适合采用瞬态动力分析，手机跌落碰撞事件归为瞬态动力学事件，分析采用的是ABAQUS显式方法（ABAQUS/Explicit）进行分析[3]。

1 瞬态动力学理论

瞬态动力学是以事件函数的载荷作为输入数据，随时间变化的位移和其他数据（应力、应变等）作为输出数据的技术。

在动力学分析时所建立的平衡方程为[4]

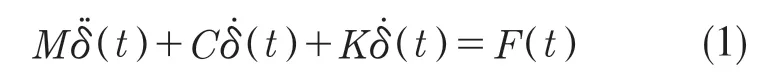
式中：F（t）——载荷向量，是时间的已知函数；δ（t）——位移向量，是时间t 的函数；（t），（t）——速度向量与加速度向量，分别是位移向量（δt）对时间t 的1 阶与2 阶导数。

由整个系统的动能

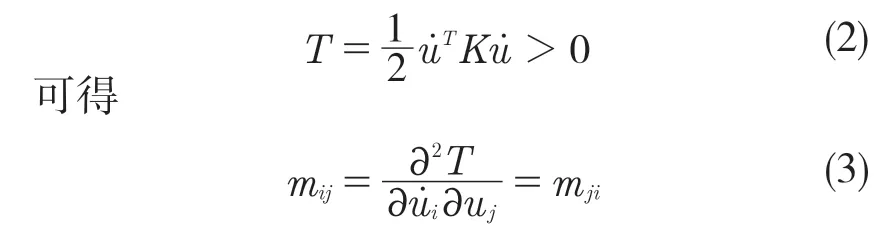
由此可得，刚度矩阵M 反映了正定的对称矩阵以及系统的动能。

由整个系统的弹性势能

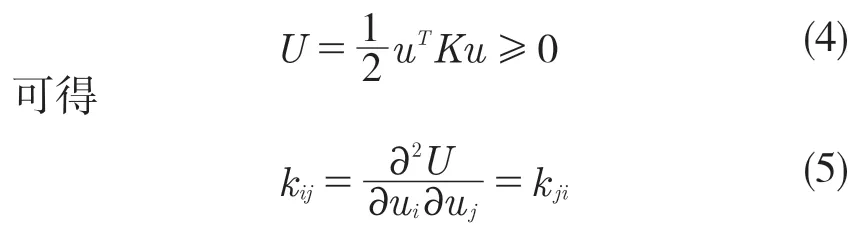
由此可得，刚度矩阵K 反映了半正定矩阵且对称以及系统的势能。

阻尼C 一般假定为黏性阻尼，其大小与速度呈正比。ABAQUS 中分为3 种不同类型的阻尼：直接模态阻尼、复合模态阻尼、瑞利阻尼。

方程（1）为瞬态动力学的基本方程，在求解该方程的过程中，ABAQUS 会对方程进行半离散化处理。ABAQUS 求解动力学问题有2 种求解方法：直接积分法与振型叠加法。直接积分法是直接对运动学方程（1）进行积分，在显式方法（ABAQUS/Explicit）中是采用中心差分法进行的计算；振型叠加法包含求解系统的固有振型和固有频率，进而求解系统的动力学响应。

在ABAQUS/Explicit 中使用直接积分的方法对上述动力学微分方程组求解，可以得到位移、速度、加速度向量，从而达到求解动力响应问题的目的[5]。

2 手机跌落碰撞仿真

2.1 三维模型建立与材料属性定义

通过对手机跌落碰撞过程仿真，求解手机在跌落过程中的速度、应力、能量等的变化规律。

首先在建模软件中绘制智能手机屏幕、机身、本体的三维模型。手机实体模型与屏幕模型如图1 所示。

图1 手机实体三维模型Fig.1 Physical 3D model of mobile phone

装配完成之后对手机各部分进行材料定义，手机各部分材料及材料属性如表1 所示。

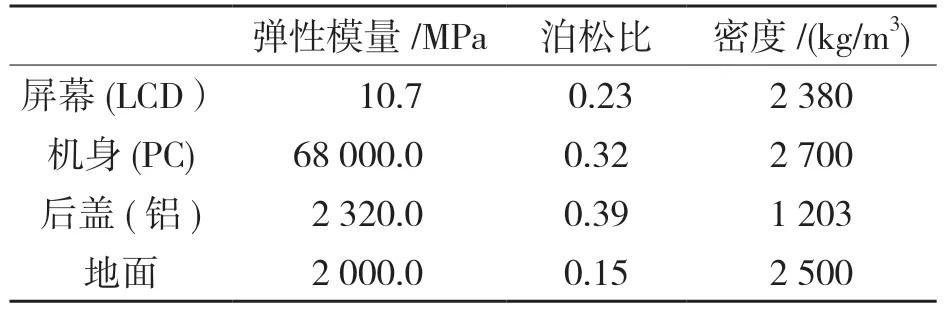
表1 材料属性Tab.1 Material properties

ABAQUS 软件中的LCD 屏幕材料与铝合金后盖属性设置如图2 所示。

图2 定义材料属性Fig.2 Define material properties

在定义材料属性之后，对模型的截面特性设置与分配界面特性操作。

2.2 模型分析设置

由于进行的是手机跌落碰撞瞬态动力学分析，并且采用显式方法，所以在软件设置中选择ABAQUS/Explicit 模块，分析步选择Dynamic，Explicit 显式动态分析步，分析时间为2 s，启动几何非线性设置，具体设置界面如图3 所示。

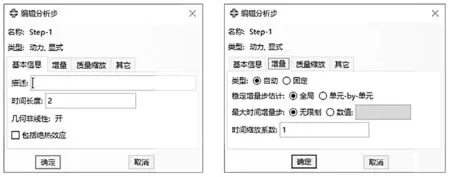
图3 显式动态分析步设置Fig.3 Explicit dynamic analysis step settings

2.3 接触属性设置

将手机实体与地面模型之间的接触属性在法向方向定义为硬接触属性，切向方向的摩擦因子值定义为0.5。

要模拟手机自然跌落状态，需要对手机模型施加一个重力载荷，重力场大小等于重力加速度大小，为-9.8 m/s2，方向朝向地面。

在仿真分析过程中，对于一个很复杂的函数在全域内直接进行逼近求解是很复杂且难以实现的，然而当我们将其定义域划分为有限数量的小段，且在每一段内采用较低阶次的插值计算，在每一段的交界处满足一定的连续性条件，就可以方便地得到在全域内一个较好的插值结果，所以在有限元仿真过程中我们需要对模型进行网格划分，使其首先在每一个网格内进行求解[6]。

在仿真计算中，通常较多的节点数最终会得到更高的计算精度，当然在复杂的几何模型中，复杂的三维模型无法被精确的六面体单元所堆砌，从而会选择四面体单元。本仿真模型结构较为简单，最终我们选择采用六面体单元进行网格划分，并且还能达到提高计算精度的目的[2]。仿真模型的六面体网格划分结果如图4 所示。

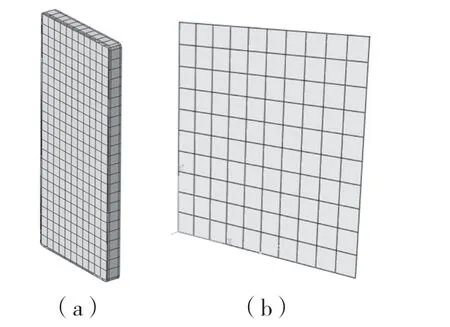
图4 模型网格划分Fig.4 Model meshing

网划分结束后对模型进行提交分析。

3 瞬态动力学分析结果

分析结束后对计算结果进行了提取整理。手机仿真模型从0.8 m 低空跌落，至最终落地时间为1.814 s，共与地面碰撞3 次，其中在0.43 s 时与地面发生第1 次碰撞，在1.098 s 时与地面发生第2 次碰撞，且开始反弹旋转，最终在1.752 s时到达最终状态。手机模型下落过程中的位置形态如图5 所示。

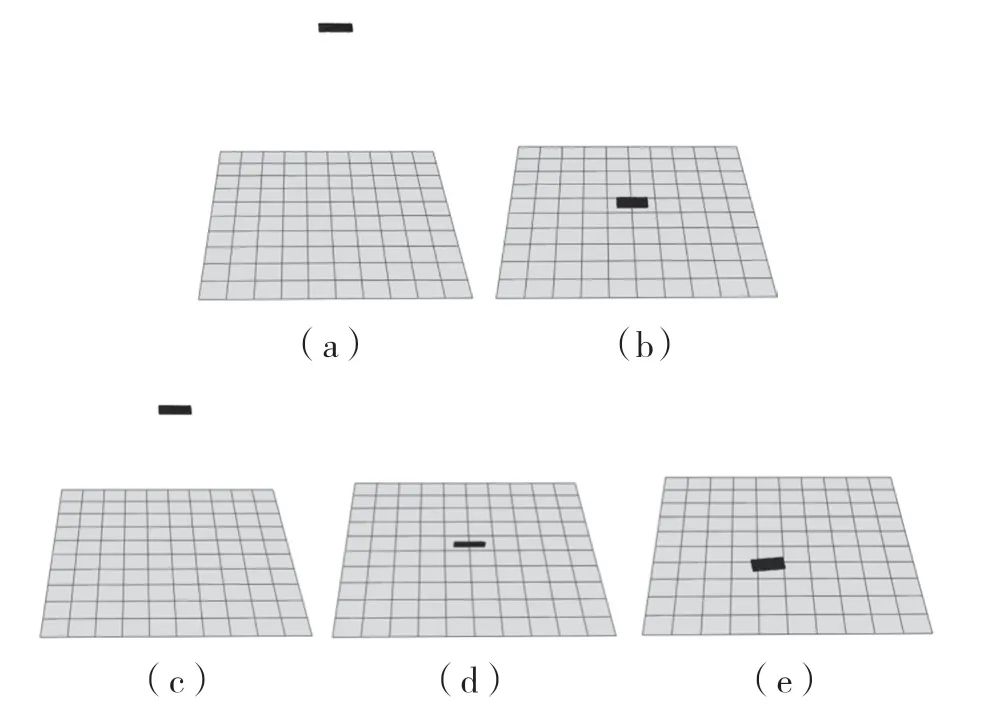
图5 手机跌落过程中的位置形态变化Fig.5 Position and shape change of mobile phone during drop

手机跌落过程中的最大主应力分布如图6 所示。由图6 可以发现，第1 次发生碰撞时由于手机为水平下落，导致应力分布较为均匀，手机各部分受力较小，图6（c）为手机第1 次跌落结束上升到最高高度的状态；图6（d）为第2 次跌落，手机开始发生倾斜，应力分布发生偏向一测现象，此时相较第1 次跌落碰撞时的最大应力明显增大，之后手机开始旋转上升，应力分布如图6（e）、图6（f）所示；第3 次跌落时，由于边角先发生碰撞，导致此时的手机最大应力达到最大，相较于前两次碰撞的应力增大了一至两个数量级左右，如图6（g）、图6（h）所示；图6（i）为手机达到最终稳定状态。

图6 直观反映出手机下落过程中，最大应力的绝对值逐渐增大，而在手机上升过程中，手机承受的最大应力的绝对值在逐渐较小。

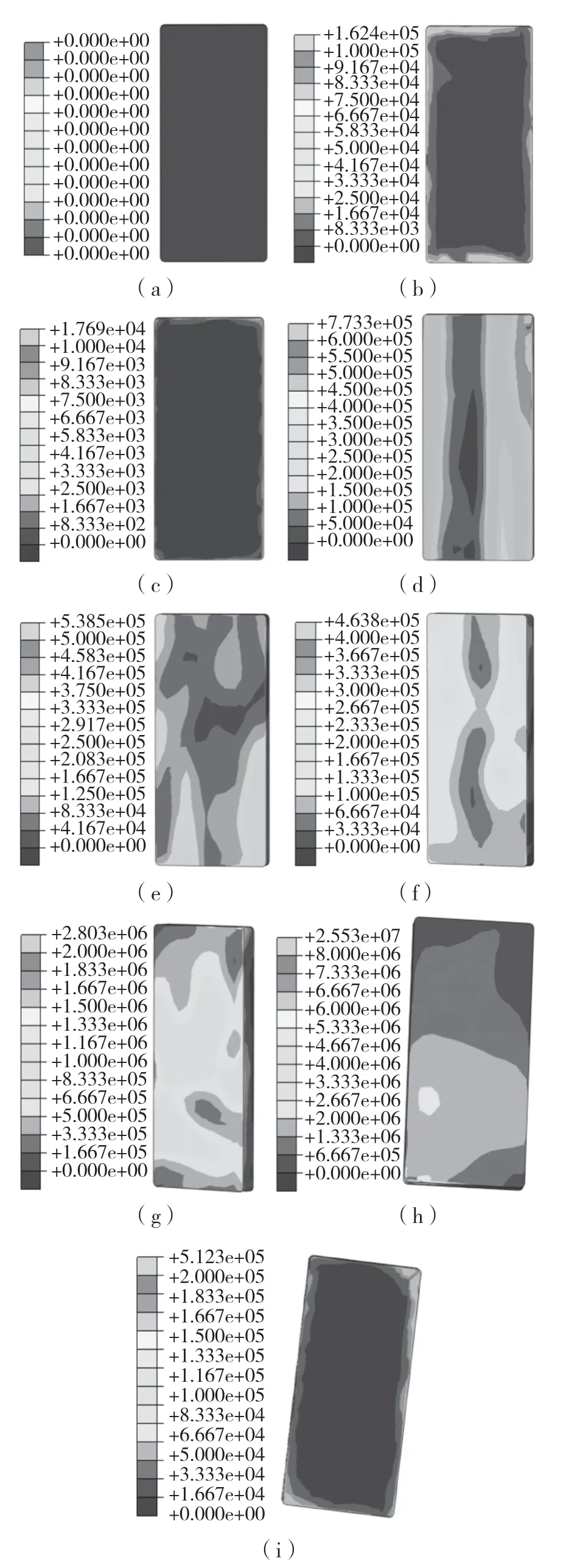
图6 跌落过程应力变化Fig.6 Stress changes during drop

手机跌落过程中的应变云图如图7 所示。

图7 应变云图Fig.7 Strain cloud diagram

在第3 次碰撞时，LCD 屏幕的最大应变已经达到了0.179 2 mm，此时已经远远大于LCD 玻璃屏幕失效判据，LCD 屏幕失效风险很高。

4 结语

本文通过对智能手机自由跌落碰撞过程进行CAE 仿真，深入分析了手机跌落过程中应力和应变的变化，能够在手机模型设计阶段提供参考，并且可以对之后的模型修改提供依据。可以在手机实体生产出来之前对手机设计进行预测，判断其是否存在缺陷，提早进行设计修改。这样不仅缩短了产品的研发周期，也大大降低了产品的研发成本。