关节臂式坐标测量机热误差仿真建模及补偿
曾志江,高贯斌,马文金
(650500 云南省 昆明市 昆明理工大学 机电工程学院)
0 引言
随着现代制造水平的不断提高,对精密仪器的精度要求也越来越高,温度变化对精密仪器的测量精度影响十分显著[1]。关节臂式坐标测量机是一种新型的多自由度非正交式坐标系测量机,由于其灵活性高和便携性好,现已逐步应用于航空航天、机械制造、汽车船舶等领域。测量精度是制约关节臂式坐标测量机发展的一个主要因素,温度变化带来的热变形误差是影响关节臂式坐标测量机精度的重要因素[2-3],采取相应措施减小其影响对提高关节臂式坐标测量机的精度具有重要意义。
由于热误差补偿研究对硬件条件要求高,且需要长时间、大数据样本的测试分析,目前关节臂式坐标测量机热误差研究的文献较少。Santolaria[4]等在不同的温度下对关节臂式坐标测量机的运动学参数进行辨识,以20 ℃下的运动学参数作为参考基准值,采用四次多项式拟合预测其它温度下运动学参数相对于参考值的偏差,并补偿到关节臂式坐标测量机的控制器中,实现热误差补偿。胡毅[5]通过对一标准杆件的长度测量,分析了在环境温度改变及内部热源对测量精度的影响,并建立了基于神经网络的补偿模型对关节臂式坐标测量机热变形误差进行修正。于连栋[6]等提出了一种新型圆光栅测角误差补偿方法,基于谐波方法建立了含有环境温度影响因子的圆光栅测角误差补偿模型,以提高关节臂式坐标测量机的测量精度。
综上所述,目前对关节臂式坐标测量机热误差研究均是通过实验的方法获得温度变化后的运动学参数,并研究运动学参数变化量与温度的关系,尚缺乏数值模拟与理论上的支撑,温度变化对关节臂式坐标测量机测量精度影响的机理还不够明确。
为探明关节臂式坐标测量机热变形规律及其对运动学参数的影响,本文建立了关节臂式坐标测量机的有限元分析模型,得到了热变形分布图,提出一种虚拟坐标测量方法,在有限元分析后测得关节臂式坐标测量机的运动学参数,并以此建立热误差模型,验证了模型的正确性。
1 关节臂式坐标测量机建模与有限元分析
1.1 运动学建模
关节臂式坐标测量机是由连杆串联多个关节组成的一种空间开链式机构。通常采用D-H(Denavit-Hartenberg)法来建立关节臂式坐标测量机的运动学模型[7]。运动学模型实现了关节臂式坐标测量机关节空间到坐标空间的变换,是关节臂式坐标测量机测量的数学基础。
本文实验对象如图1 所示。关节臂的型号为ROMER RA-7125。根据D-H 法在各关节处建立了关节臂式坐标测量机的坐标系统,如图2 所示。通过计算关节臂式坐标测量机两个相邻关节间的齐次变换矩阵Ti-1,i,见式(1),逐个相邻关节变换矩阵连乘后再乘以测头偏置(lx,ly,lz,1)T,见式(2),就可得到末端测头中心在基坐标系下的坐标(x,y,z,1)T。

图1 关节臂式坐标测量机Fig.1 Articulated arm coordinate measuring machine
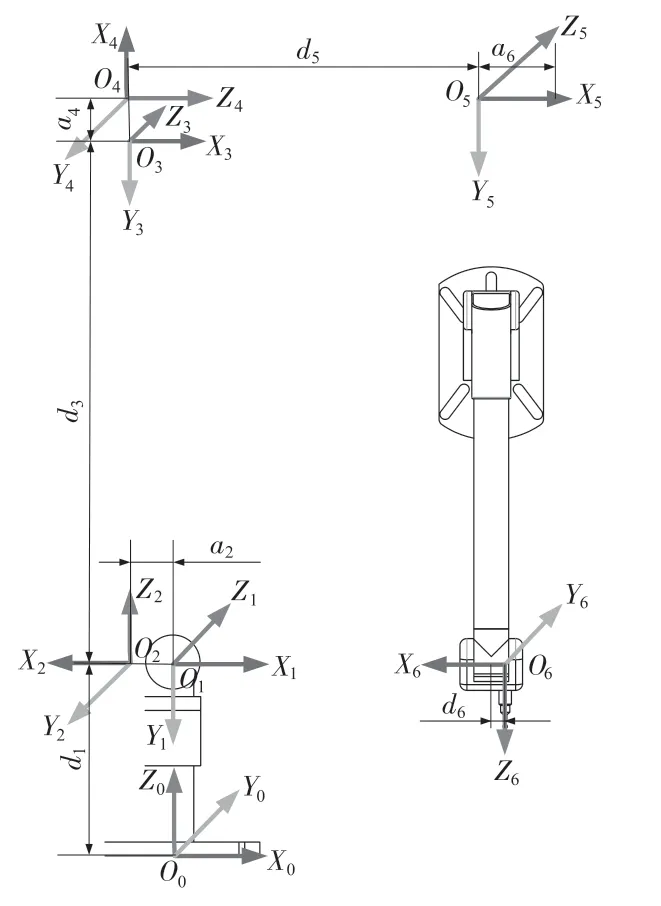
图2 关节臂式坐标测量机的坐标系统图Fig.2 Coordinate systems of articulated arm coordinate measuring machine
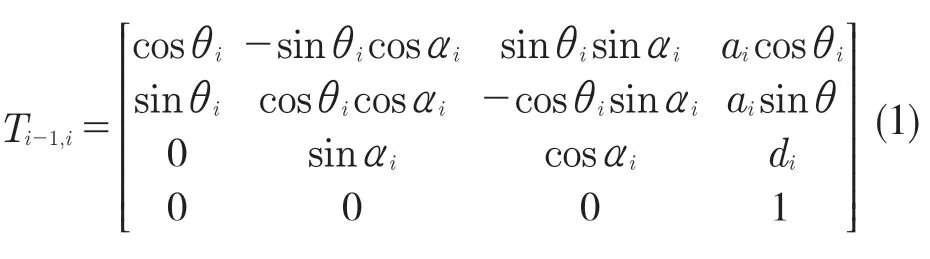
式中:i=1~6——关节序号;θi——关节转角,为变量,其值可由安装在轴端的编码器测得;αi——关节扭转角;di——连杆偏距;ai——杆长。
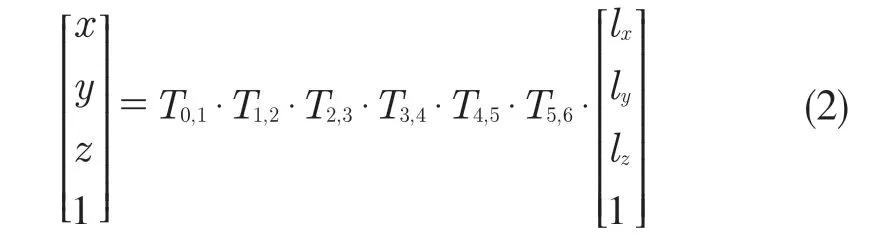
式中:lx,ly,lz——测头中心在第6 关节坐标系中的位置。
1.2 关节臂式坐标测量机热误差有限元分析
关节臂式坐标测量机的工作温度范围通常为10~40 ℃,本文以25 ℃为参考基准,在10~40 ℃范围内分析关节臂式坐标测量机各关节运动学参数随环境温度变化的规律。
相比实际关节臂式坐标测量机,对外置平衡机构、外壳、防护罩部分进行简化,建立简化的三维模型。这些零件对运动学参数的热变形没有影响,简化的模型不影响热误差分析结果。关节臂式坐标测量机主要由2 种材料组成,关节处的零件主要为7075 铝合金,连杆为碳纤维,相关属性如表1 所示。关节臂式坐标测量机的运动学参数如表2 所示。
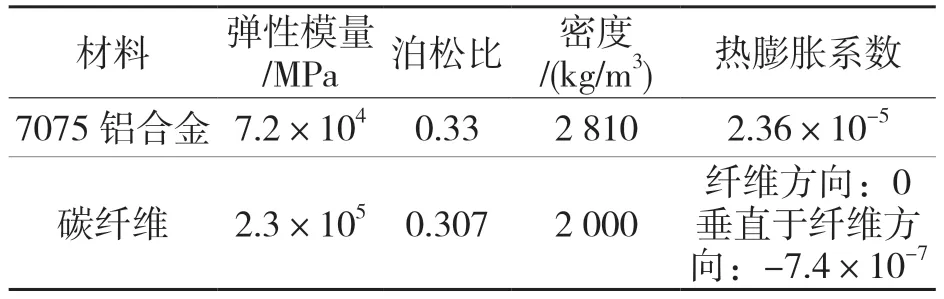
表1 关节臂式坐标测量机主要材料属性Tab.1 Properties of main materials of articulated arm coordinate measuring machine
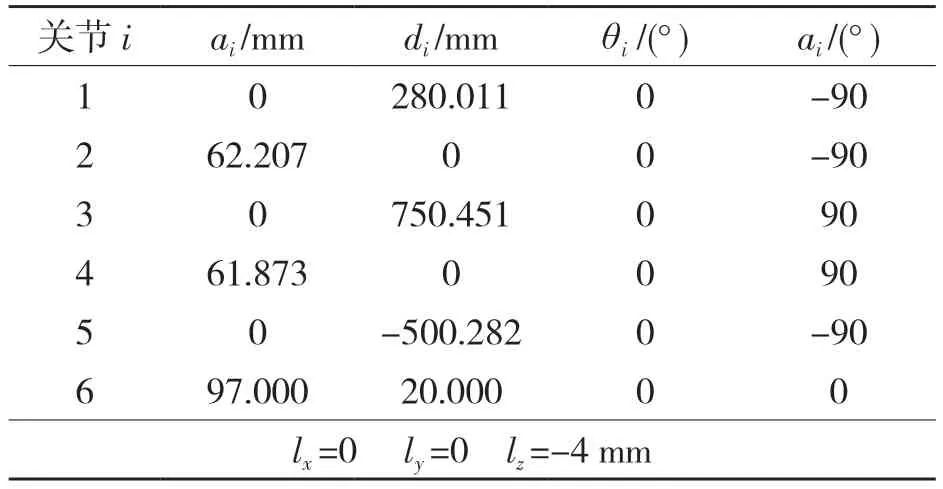
表2 运动学参数值Tab.2 Values of kinematic parameters
将关节臂式坐标测量机简化三维模型导入有限元分析软件,对模型的各部分材料进行设置。ANSYS 自动网格划分的网格自适应能力较强,本文采用其自动网格划分,网格大小也采用智能设置。固定关节臂式坐标测量机基座,并施加温度载荷,分析施加温度载荷后关节臂式坐标测量机的整体形变。
本文在3 种位姿下分析关节臂式坐标测量机热变形情况。3 种位姿分别采取较近、适中、较远位置,以此覆盖关节臂式坐标测量机的主要工作空间。在关节臂式坐标测量机的工作温度范围10~40 ℃下每隔3 ℃采集一次数据做分析,由于40 ℃下关节臂式坐标测量机的热变形误差最大,所以选用40 ℃下3 个位姿的热变形图作为例子展示其热变形情况,分别如图3—图5 所示。
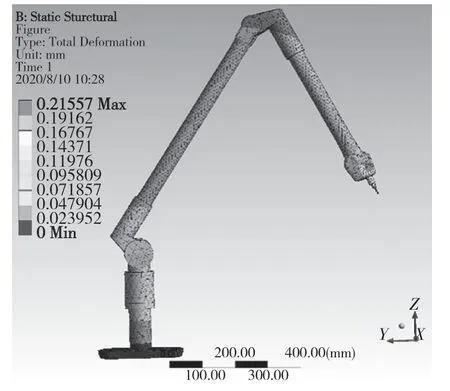
图3 40 ℃下位姿一热变形Fig.3 Thermal deformation of pose 1 at 40 ℃
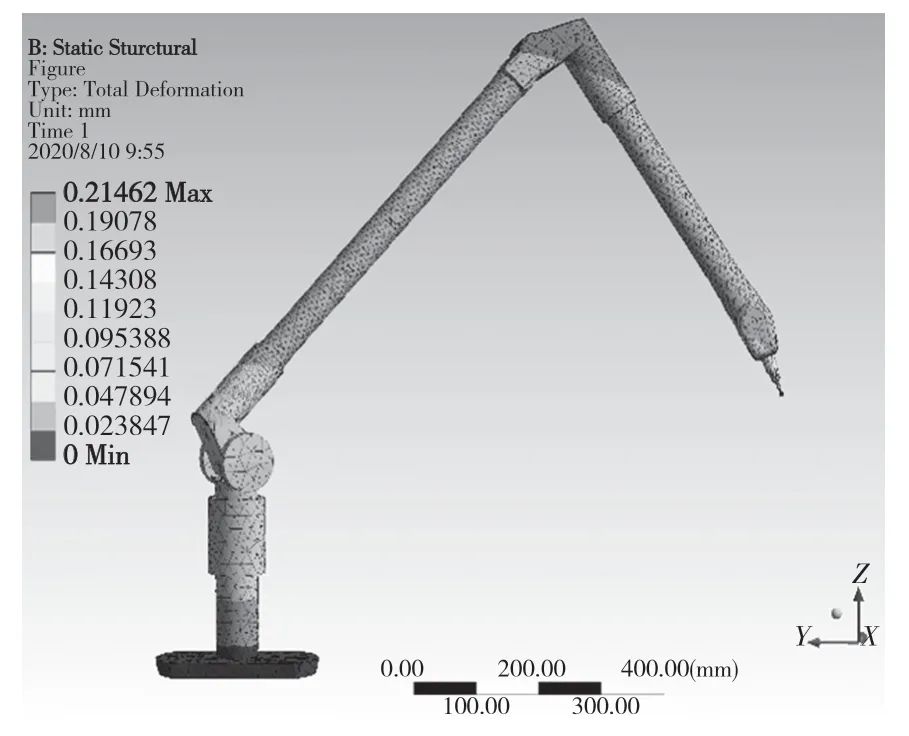
图4 40 ℃下位姿二热变形Fig.4 Thermal deformation of pose 2 at 40 ℃
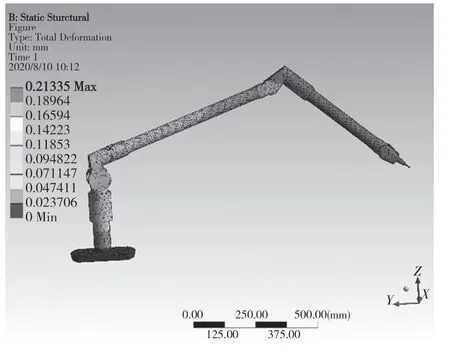
图5 40 ℃下位姿三热变形Fig.5 Thermal deformation of pose 3 at 40 ℃
由图3—图5 可以看到,随着末端位置远离基座,热变形越大,热变形随着机构呈现逐级放大的情况[8-9],在较远位置的最大变形量为0.213 mm。
2 热误差补偿建模与仿真验证
2.1 关节空间参数虚拟测量及热误差补偿模型建立
为量化热误差对关节臂式坐标测量机参数的影响,提出一种虚拟坐标测量方法。基于坐标测量原理提取有限元分析后的节点位置数据,利用点拟合线和面等几何元素,再通过对拟合的几何元素之间距离和夹角的计算,得到关节臂式坐标测量机的运动学参数。如图6 所示,通过虚拟测量,发现关节臂式坐标测量机的角度参数θi,αi不变,而长度参数di,ai变化较明显。
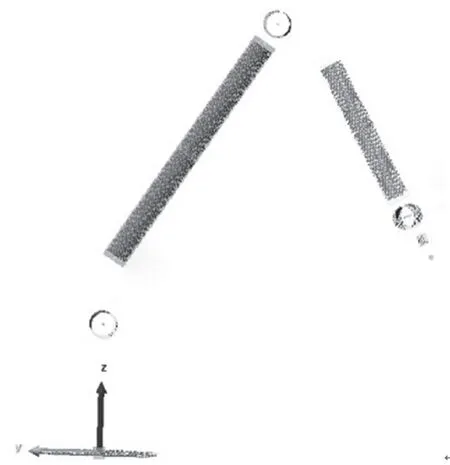
图6 有限元节点提取及几何元素拟合Fig.6 Extraction of finite element nodes and geometric element fitting
由于温度变化对长度为0 的几何参数不会产生影响,所以本文只对关节臂式坐标测量机中不为0 的长度量d1,d3,d5,d6,a2,a4,a6进行测量,分析温度变化对它们的影响规律。经分析发现,关节臂式坐标测量机3 个位姿在同一温度下的各参数的测量值基本一致,取3 个位姿测量的平均值。在不同温度下测量得到的结果如表3 所示。可以看出,随着温度的升高,长度参数总体呈逐渐增加的趋势。
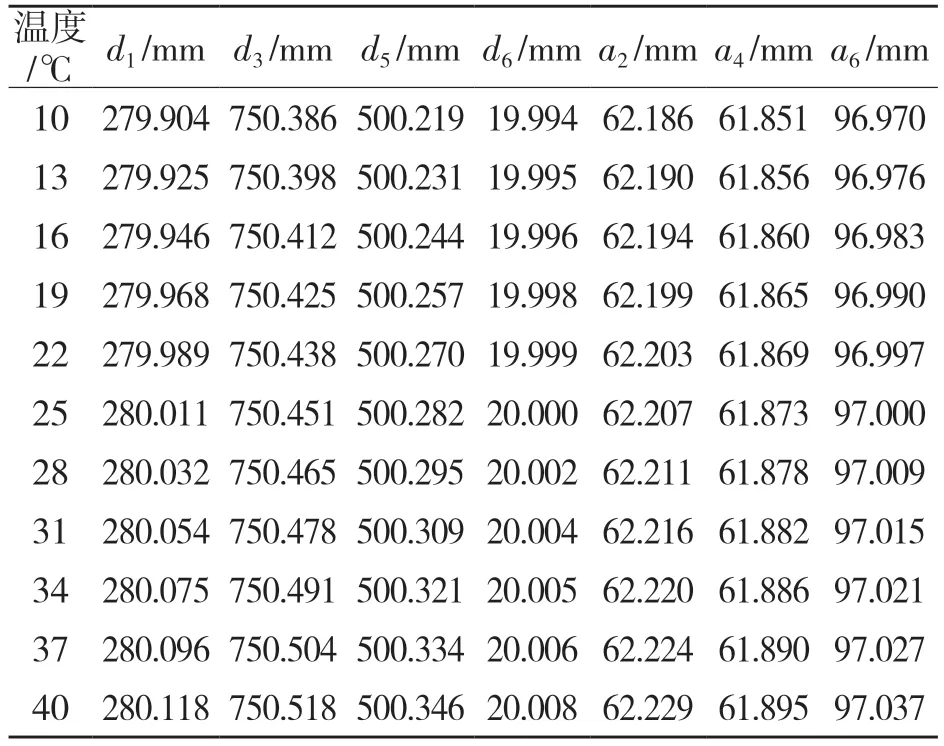
表3 各温度下长度参数Tab.3 Length parameters at different temperatures
根据表3 中长度参数值的变化可发现,长度参数随温度升高呈近似线性增加的现象。由材料平均线膨胀系数计算式[10]对关节臂式坐标测量机6 个关节各用一个对应的温度系数Ci来描述长度参数随温度变化的关系,如式(3)所示。根据虚拟测量的结果计算得到各关节的温度系数如表4 所示。通过各关节温度系数可以计算各关节在工作温度范围内任意温度下的长度参数。
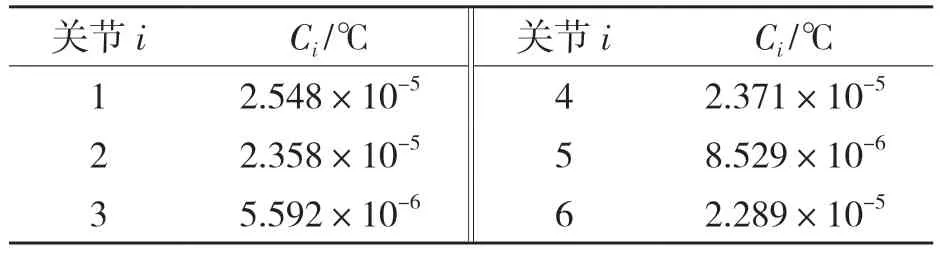
表4 各关节温度系数Tab.4 Temperature coefficients of the joints
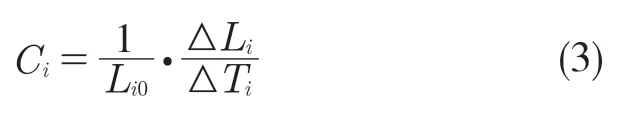
式中:L0——基准温度下的长度;ΔL ——长度的变化量;ΔT——温度的变化量;i=1~6——关节1~6。
由有限元分析后得到温度系数Ci可计算关节臂式坐标测量机各关节在工作温度范围内任意温度下的长度参数变化量,从而建立基于运动学参数的关节臂式坐标测量机热误差补偿模型,如式(4)和式(5)。
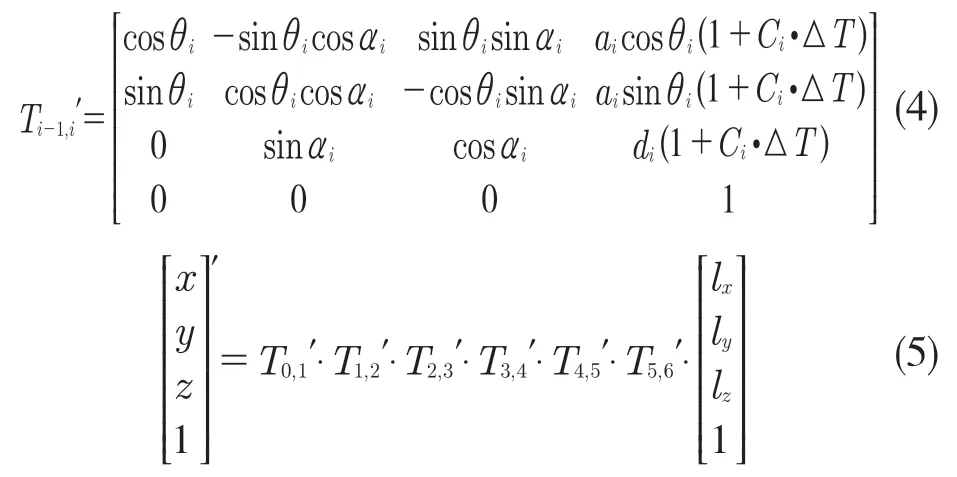
式中:i=1~6 ——关节1~6。
2.2 热误差仿真补偿
使用式(5)中给出的误差补偿模型,对关节臂式坐标测量机热误差进行补偿仿真。为了避免使用建立误差补偿模型时用过的温度数据,分别在15,20,30,35 ℃下通过虚拟测量的方法采集数据并进行验证。将25 ℃作为参考温度,在此温度下位姿一、二、三的测头中心坐标分别为P1(-44.026,-705.601,448.854),P2(105.438,-1 186.060,230.614),P3(252.507,-812.426,356.097)。六自由度关节臂式坐标测量机是冗余机构,测头中心保持在同一个位置时,可以通过改变各关节的转角来改变其姿态。为了将姿态对测量结果的影响纳入进来,在上述P1,P2,P3位置处,通过运动学逆解计算出每个位置的任意5 组关节转角,将这些关节角代入式(5),可以分别计算出热误差补偿前后15,20,30,35℃下的末端位置。对每个位置的5 组末端位置数据分别求其平均值作为该温度下补偿后的位置,3 个补偿后的位置再计算相互之间的空间距离,通过在15,20,30,35 ℃下的仿真距离,分析与补偿后的距离差值验证空间距离精度提高的情况。图7—图9 分别为距离1、距离2、距离3在上述验证组温度下补偿前后空间距离精度对比图,热误差补偿后3个空间距离精度分别从0.025,0.024,0.035 mm 提高到了0.008,0.012,0.014 mm,空间距离精度得到显著提高。
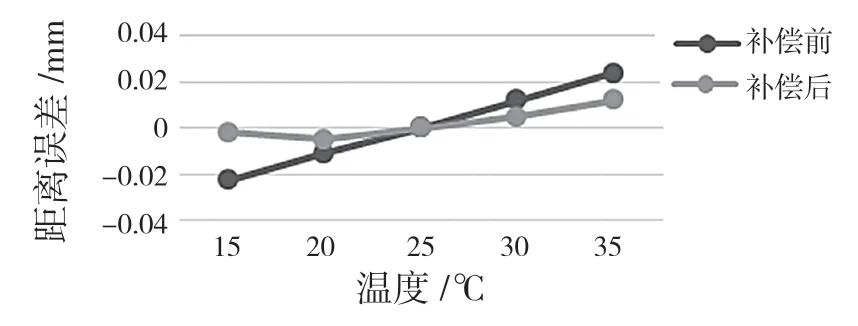
图7 距离1 补偿前后精度对比Fig.7 Accuracy comparison before and after compensation for distance 1
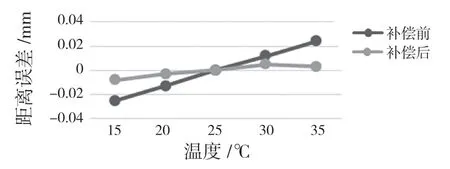
图8 距离2 补偿前后精度对比Fig.8 Accuracy comparison before and after compensation for distance 2
3 结论
对关节臂式坐标测量机的热误差进行有限元分析,得到了热变形分布图;提出一种虚拟坐标测量方法测得热变形后的运动学参数随温度的变化规律,对每个关节提出一个温度系数并建立相应的热误差补偿模型,使关节臂式坐标测量机的精度及稳定性得到了极大的提高。
采用有限元分析手段及数值仿真技术对关节臂式坐标测量机热误差进行分析,弥补了目前缺乏数值模拟与理论支撑的缺陷;通过运动学参数的虚拟测量进一步明确了热误差对关节臂式坐标测量机精度的影响机理,对关节臂式坐标测量机后续的热误差分析提供了有效指导。

