基于深度时间序列特征融合的西安市2015—2020年供暖季雾霾重污染过程预警
王英,冉进业,张今,杨鑫,张浩
(1 西南大学化学化工学院,重庆 400715;2 西南大学计算机与信息科学学院,重庆 400715;3 重庆理工大学化学化工学院,重庆 400054)
目前,PM浓度预测方法包括基于大气化学反应和传质模型的机理方法和数据驱动的统计方法。PM微观形成过程涉及复杂的气-固相界面非均相化学反应和气-液、气-固传质过程,宏观上受本地积累、区域传输和二次转化的共同影响。前体与大气边界层气象要素双向协同机制导致我国重点区域PM重污染成霾速度快、污染峰值高、阶段性变化明显,给机理模型的建立带来了巨大困难。在PM重污染形成机理尚未十分明晰的情况下,数据驱动方法中的机器学习模型可利用环境大数据推断PM本地积累、区域传输和二次转化强度,模拟雾霾重污染时空演化规律,建立较为准确的重污染形成机制代理模型。常用的机器学习模型有多元线性回归(multivariate linear regression model, MLR)、 随 机 森 林 (random forest,RF)、 支 持 向 量 机(support vector machine,SVM)、隐马尔可夫模型(hidden Markov model,HMM)以及人工神经网络(artificial neural network,ANN)等。相对上述传统统计模型,以卷积神经网络(convolutional neural networks,CNN)和递归神经网络(recurrent neural network,RNN)为代表的深度学习模型可使用多重非线性变换构成的复合处理层对数据进行高层抽象,在图像和语音识别方面取得了突破性进展。然而,传统RNN 在处理浓度变化巨大的雾霾重污染时间序列数据时往往无法连接关键信息,导致较大的预测误差。与传统RNN 相比,长短期记忆网络(long short-term memory,LSTM)通过增加隐含状态不仅可以解决传统RNN 梯度爆炸与梯度消失问题,同时可以提取时间序列的长期依赖关系,目前被广泛用于空气污染浓度预测领域。
精确预测雾霾重污染事件中PM浓度的最终目标是采取有效措施最大限度消除污染带来的社会和经济影响,对此需要较好解释PM浓度影响因素的相关参数与目标PM浓度的关系,因此采用的数据驱动预测模型参数可解释性尤为重要。LSTM 虽具有较好的预测效果,但是模型参数的可解释性欠佳;而MLR 模型可以较好解释输入变量与目标变量之间的关系。因此,为有效解释LSTM提取的时间序列深度特征并获取各变量对未来PM浓度的影响,本文提出了深度时间序列特征融合模型(long short-term memory and multivariate linear regression,LSTM-MLR)。该模型通过LSTM分别提取NO、SO等空气污染物的浓度以及相对湿度、风速等气象因素的复杂信息;使用MLR 融合深度学习模型提取的时间序列深度特征,构建空气污染物的浓度、气象因素与未来PM浓度之间的函数关系进而简化预测背后的推理过程。通过MLR 模型参数的正负与绝对值大小表示当前污染物浓度、气象因子与未来雾霾浓度之间的相关性和贡献度,从而可以较好解释输入变量与目标雾霾浓度之间的关系。
汾渭平原包括山西省、陕西省和河南省共11个地级市,全面静风率为35%,冬季静风率高达45%。因其地理地形、气象条件、产业布局和能源结构等原因,区域内污染物排放强度持续累积,多个城市在全国重点城市空气质量排名倒数,雾霾污染防控压力较大。在汾渭平原城市群中,西安是最具区域影响力和国际知名度的城市。因此,本文使用所提出的深度时间序列特征融合模型(LSTMMLR)对西安市2015年1月至2020年3月共6个供暖季雾霾重污染事件中的PM浓度进行3~24h 预测,以实现对雾霾重污染的准确预测并为其采取消峰降速紧急措施提供数据支撑。
1 研究方法
1.1 LSTM模型
LSTM 通过在隐藏层中加入记忆单元来控制时间序列数据的记忆信息,使用3 个门结构(遗忘门、输入门、输出门)在隐藏层的不同单元之间进行信息传输,从而控制历史信息和当前信息的记忆和遗忘程度,其网络的结构如图1所示。
图1中,是式(1)的sigmoid函数,输出为介于0 和1 之间的值。0 表示“全部不通过”,1 表示“全部通过”,通过式(2)中的双曲正切函数来克服梯度消失的问题,其输入和输出见式(3)~式(8)。

图1 LSTM结构
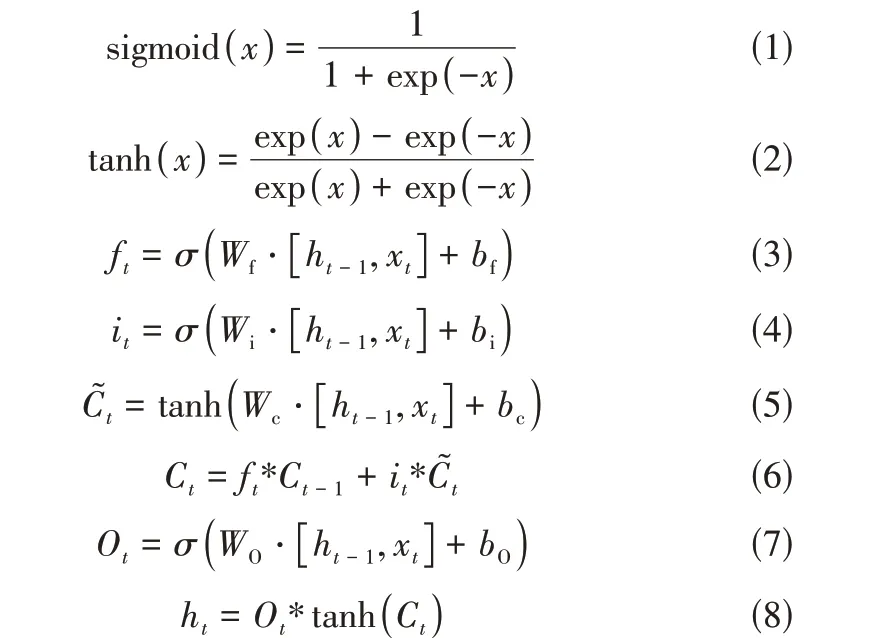
式 中,、、、为 输 入 权 重;、、、为偏置;下角标为当前时间;下角标-1为先前时间;为输入;为输出;为单元状态。
1.2 MLR模型
MLR 研究因变量与多个自变量(解释变量)之间的依存关系,常用于数据序列的预测及分类研究。模型的一般形式如式(9)所示。
2.3 两组治疗前后SF-36分值比较 治疗前两组SF-36分值对比,差异无统计学意义(P>0.05);治疗2周后两组SF-36分值均较治疗前有所提高,且观察组高于对照组,差异有统计学意义(P<0.05)。见表4。

式中,为常数;,,…,a为回归系数,回归系数的正负性代表该解释变量对因变量的正负相关性,绝对值大小代表该解释变量对因变量的贡献度。
1.3 LSTM-MLR模型
为提高PM预测精度和模型可解释性,使用具有不同超参数结构的LSTM单元提取时间序列输入的深度特征,通过逐步线性回归筛选LSTM提取的时间序列特征(图2):①分别对LSTM输出的各个特征进行-检验以验证LSTM 输出与PM浓度之间的线性关系是否显著;②根据显著程度由高到低对LSTM输出特征进行排序;③按特征顺序依次进行-检验,观察对应的-value值是否小于0.05,否则删除该变量继续进行-检验直至每一个变量的-value 值均小于0.05;④利用MLR 对筛选后时间序列深度特征数据进行融合,预测未来3h、6h、12h和24h的PM浓度。

图2 LSTM-MLR特征融合
2 数据处理
2.1 数据来源与概述
本文所用数据为2015年1月—2020年3月西安市13 个国控站点的空气质量监测数据和西安咸阳国际机场气象监测数据。西安地处关中平原,南方被秦岭山脉阻隔,北方有黄土高原,西北部为秦岭与黄土高原结合部,东部为潼关与黄河形成的通风口,地形较为复杂,冬季静风频率较高。主导气候为温带季风气候区和亚热带季风气候,冬季供暖期雾霾污染严重。作为省会城市,西安城市建成区面积505km,城区人口超出800 万,2020 全年GDP 10020.39亿元。
西安市13 个空气质量数据监测站点设在高压开关厂、兴庆小区、纺织城、小寨、市人民体育场、高新西区、经开区、长安区、阎良区、临潼区、草滩、曲江文化产业集团以及广运潭,包括PM、PM、CO、NO、SO、O浓度数据,每小时记录1次;除去缺失数据,每个站点可用数据超过47000h,其中空气重污染样本占6.39%。气象监测数据来源于西安咸阳国际机场气象监测点,每3h记录1次。
2.2 数据预处理
由于LSTM对包含缺失值的时间序列处理效果不佳,本文使用西安13 个空气质量监测站点的PM平均浓度作为LSTM 输入时间序列的标签值,并根据式(10)对缺失值进行线性插值补充。
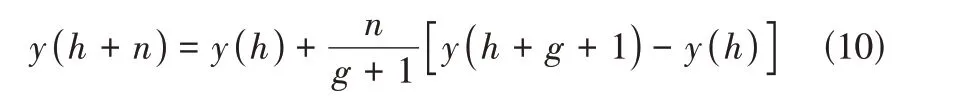
式中,(‧)为目标时间序列;为缺失值范围之前最后一个正常数据的时间戳;为缺失数据的持续时间;为缺失数据的序列号,且-1≥≥1。为了去除数据噪声,利用均值平滑法将-3:时刻雾霾浓度均值作为时刻的浓度;通过最小最大化标准法进行归一化,见式(11)。

采用如图3所示的滑动窗口的方式对数据进行标注:输入时间序列长度为滑动窗口长度(36h);间隔长度为Δ,本文设置为3h、6h、12h 和24h,标签为时间序列样本的目标值。最后,以11月1日至次年3月31日为供暖季,2015—2018年4个供暖季共12984h 数据作为训练集;2018—2019 年供暖季共3624h 作为验证集;2019—2020 年供暖季共3648h作为测试集。
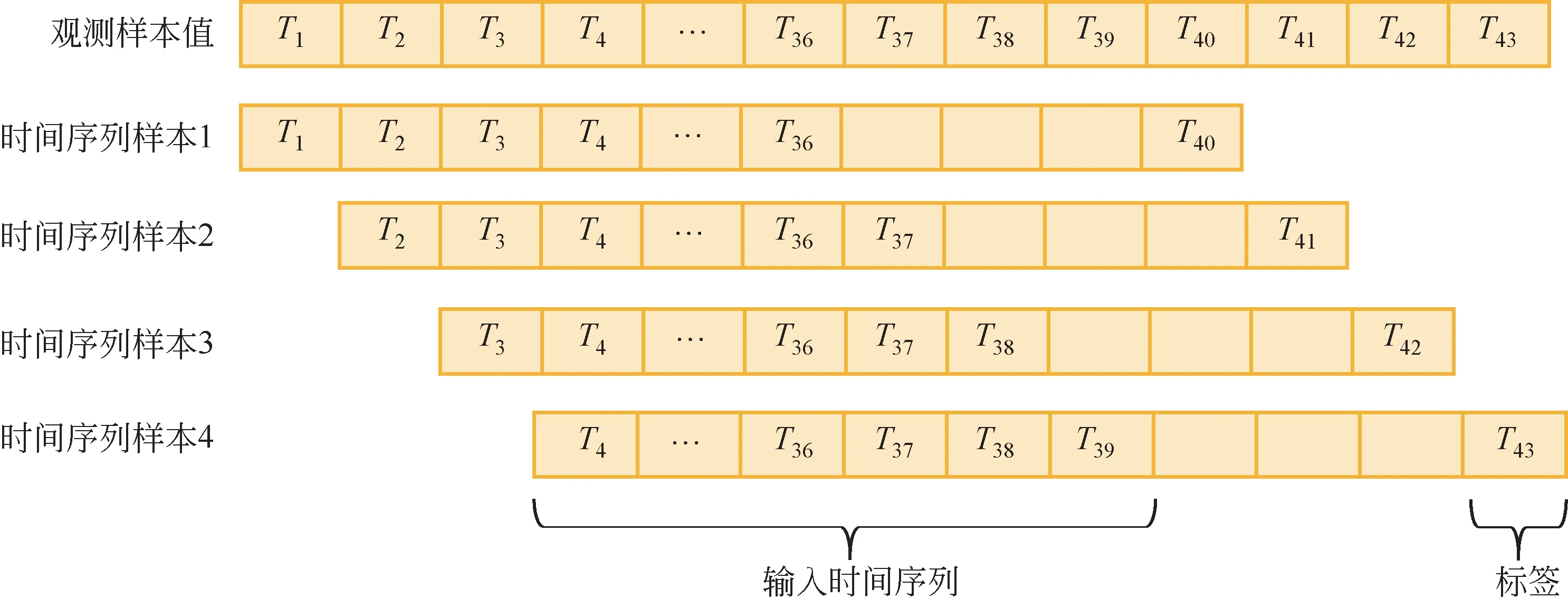
图3 滑动窗口示例图
2.3 评价矩阵
采用如下7种评价指标来评价模型的性能,见式(12)~式(18)。
平均相对误差(mean relative error,MAPE)

平均绝对误差(mean absolute error,MAE)
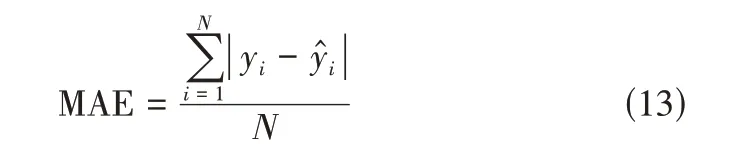
均方根误差(root mean square error,RMSE)

式中,y为第个观测数据;ŷ为第个预测值;̂ˉ为预测平均值;ˉ为观测数据平均值;为样本总数;为重污染样本的正确预测个数;为所有重污染样本观测个数;为模型预测为重污染样本个数。
3 结果与讨论
3.1 模型特征选择
LSTM-MLR 初始模型输入包括历史PM、PM、CO、NO、SO、O、水平能见度(VV)、大气温度(Temp)、露点温度()、海平面大气压()、气象站大气压()、风速(WS)、相对湿度(RH)、风向(WD)共14 个变量,模型输出为未来3h、6h、12h或24h的PM浓度预测值。通过模型显著性检验筛选特征,结果见表1:在不同预测步长模型中,所有输入变量的-value均小于0.05,即在=0.05 水平上显著,说明各个变量对目标PM浓度影响程度显著。各变量与因变量之间的相关系数同时反映了输入变量与待预测PM浓度时间序列的相关程度。本文使用相同变量组合输入比较模型,对不同时间间隔的PM浓度进行预测。由于LSTM 复杂性较高,筛选变量可有效降低LSTM-MLR 模型参数:预测步长为3h 的LSTMMLR 模型参数个数降低33.97%;预测步长为24h时,模型参数降低16.82%。
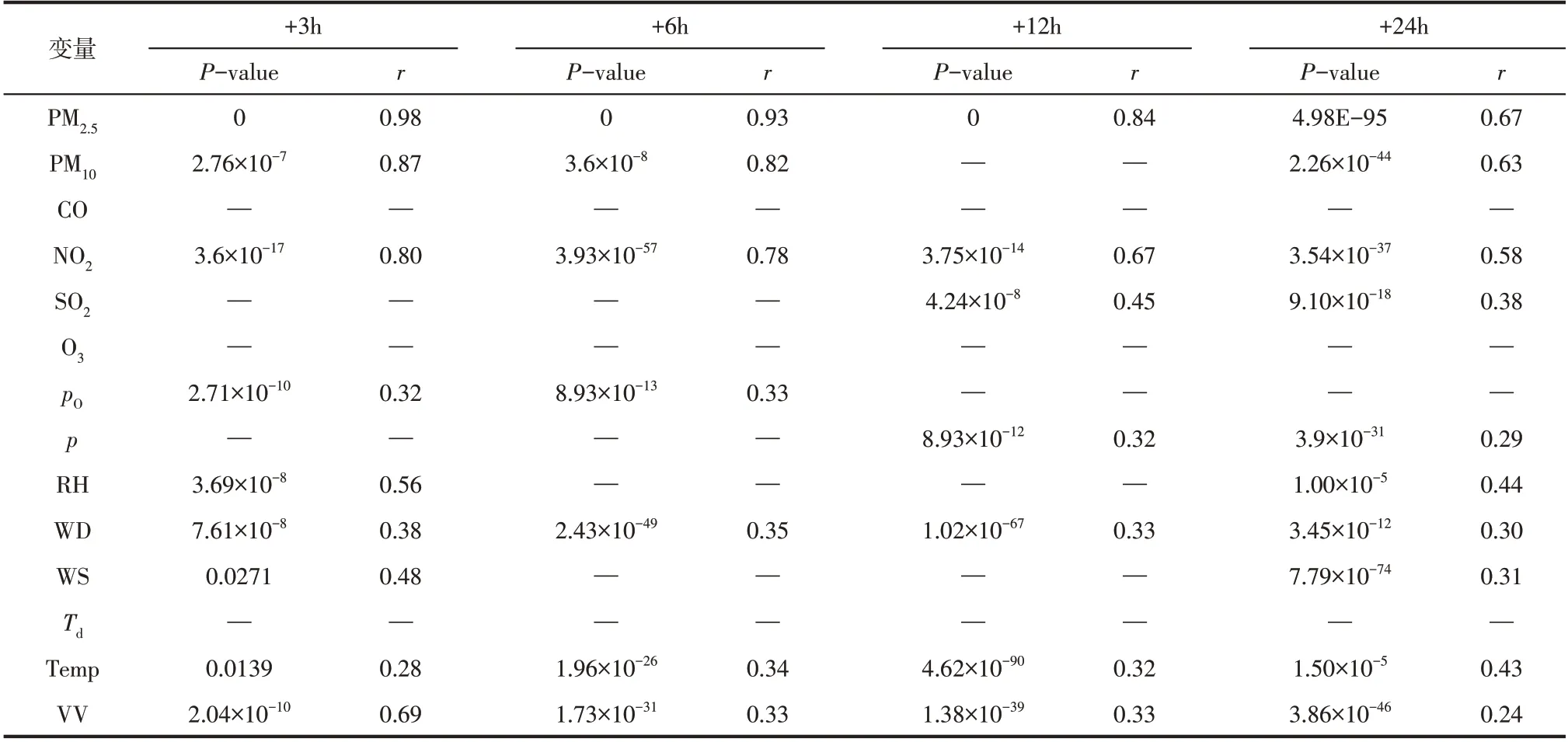
表1 LSTM-MLR特征选择结果与依据
3.2 模型预测表现
为证明LSTM-MLR 模型的先进性,建立了具有相同输入变量的RF、支持向量回归(support vector regression,SVR)、MLR、LSTM_PM、多变量LSTM(M_LSTM)和LSTM-RF(long short-term memory and random forest) 并 使 用MAPE、MAE、RMSE 和衡量模型对PM浓度的预测精度,其中,LSTM-RF表示以RF形式替换LSTM-MLR模型中MLR 形式作为特征融合层输出最终PM浓度预测值,LSTM_PM表示LSTM 中的输入变量只包含PM浓度,其他方法均是和LSTM-MLR 使用相同的多变量。LSTM-MLR、LSTM-RF、M_LSTM、LSTM_PM、MLR、SVR 及RF 的运算时间见表2。在离线训练过程中,LSTM-MLR 的运算时间同其余模型存在较大差异,比如,同M_LSTM与LSTMRF相比分别降低了25.75%与44.17%;在单样本在线预测过程中,LSTM-MLR 与其余模型的预测速度差异较小,均在1s内完成单样本在线预测。7类模型在预测步长为12h 时对某雾霾重污染事件中PM浓度的预测结果如图4所示。当预测步长分别为3h、6h、12h 和24h 时,各模型MAPE、MAE、RMSE、R见表3,最优结果用粗体标出。由表3可知,在预测间隔为3h、6h、12h时,LSTM-MLR预测精度最高。在预测间隔为24h时,MLR模型的误差最小,但与LSTM-MLR模型相差不大。

表3 不同预测步长时模型全浓度范围内的预测误差比较
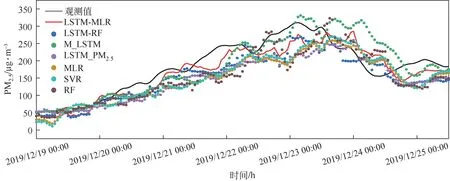
图4 预测步长为12h的各个模型对某雾霾重污染事件中PM2.5浓度预测结果
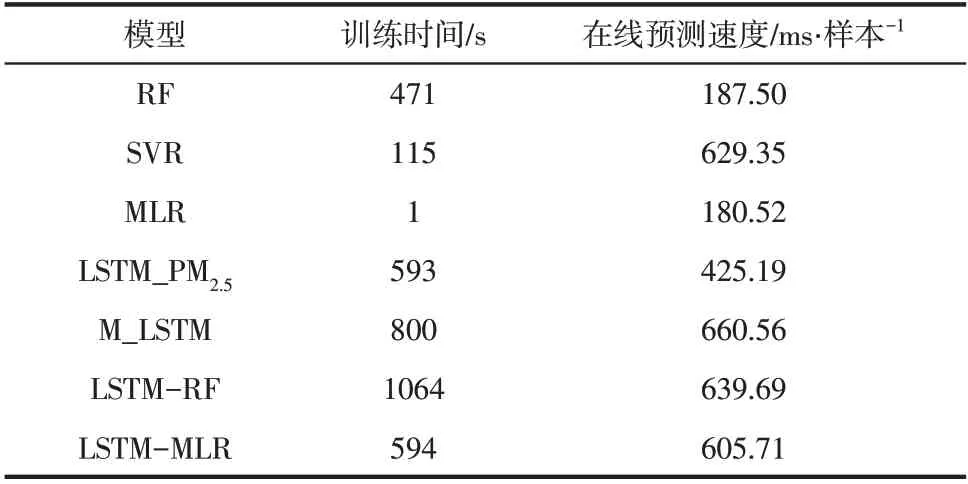
表2 模型在离线训练和在线预测阶段的运算时间差异
为进一步研究LSTM-MLR 对雾霾重污染的预测准确率,本文计算了7 类模型对PM浓度高于150μg/m样本的准确识别率等指标,包括MAPE、MAE、RMSE、R、TPR、FAR 以及SI,计算结果见表4,最优结果用粗体标出。当预测步长为3h、6h、12h 和24h 时,LSTM-MLR 模 型 的MAPE、MAE、RMSE 都明显小于MLR 与M_LSTM,R大于MLR 与M_LSTM,表明使用不同超参数LSTM 分别提取输入变量的深度时间序列特征有利于提高模型预测性能。在不同的特征融合方式中,以多元线性回归为特征融合层的LSTM-MLR 在3~24h 预测步长中的MAPE、MAE、RMSE 和R全面优于以随机森林为特征融合层的LSTM-RF。当输入变量相同时,LSTM-MLR 模型在3~24h 预测步长中的误差均大幅低于RF 和SVR。相比输入变量只包括PM时间序列的LSTM_PM,LSTM-MLR 模型的预测性能在预测步长为3~24h 时全面占优,说明增加PM前体和气象因素有利于提高PM浓度预测性能。TPR、FAR 和SI 可反映不同模型对PM重污染样本的预测性能:当预测步长为3h 时,LSTMMLR 与M_LSTM 相比对重污染样本的预测能力不占优势;当预测步长为6~24h 时,LSTM-MLR 对重污染样本的准确预报率及成功因子大幅度领先于其他方法,不同步长TPR 分别比M_LSTM 高7.15%、41.13% 和31.73%。根据不同方法的MAPE、MAE、RMSE、R、TPR、FAR 和SI 在3~24h预测步长的分布状况,可认为LSTM-MLR模型对PM重污染样本识别性能最佳,可实现对PM重污染的准确预警。表5显示不同预测步长LSTMMLR 模型评价矩阵在训练集、验证集和测试集无明显降低,说明该模型具有较好的泛化能力。
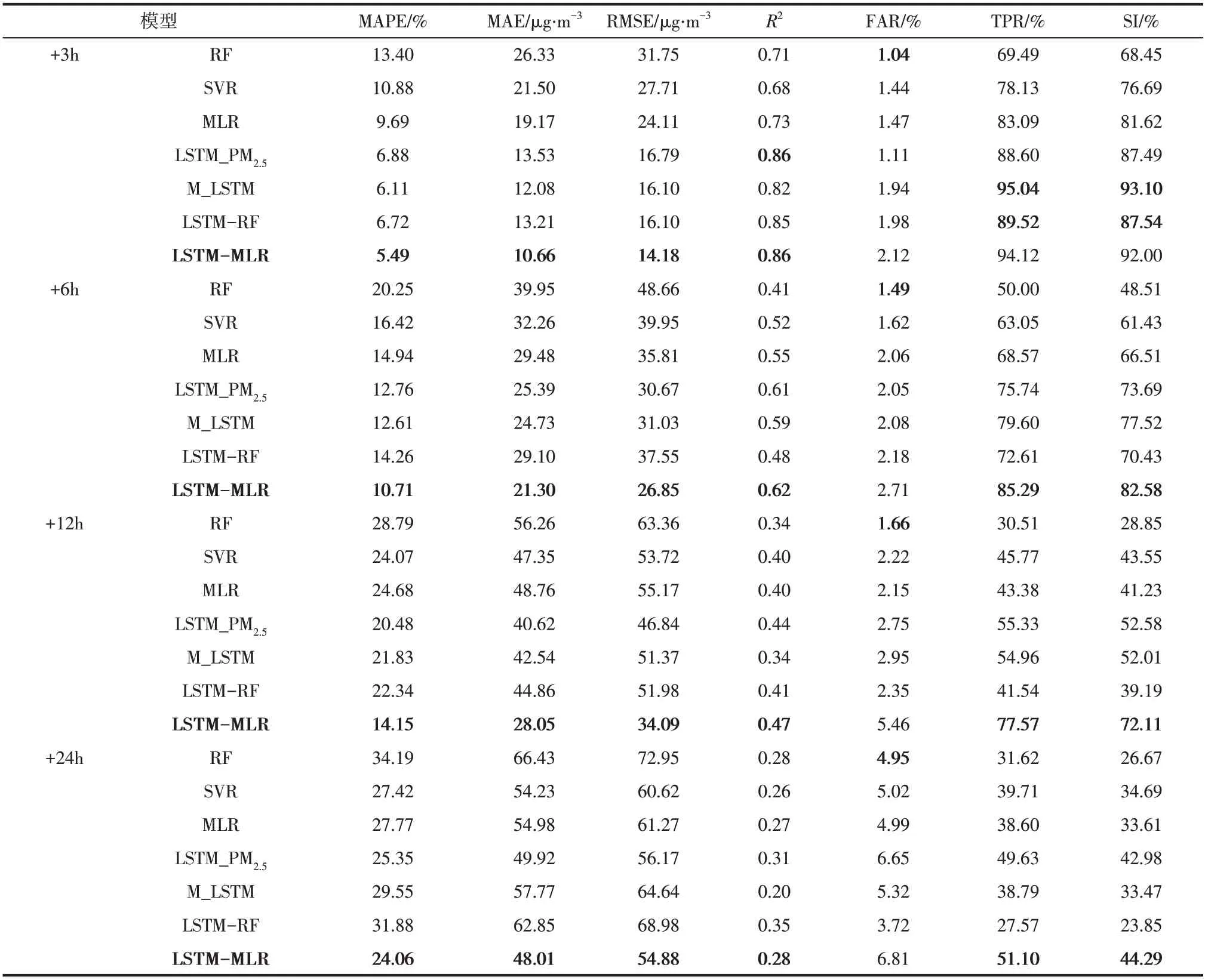
表4 PM2.5浓度高于150μg/m3时不同模型的预测结果

表5 不同的预测步长LSTM-MLR模型在训练集/验证集/测试集中的表现
3.3 LSTM-MLR模型参数解释
LSTR-MLR不仅有较高的预测性能,还具有良好的参数可解释性。表6 为4 个预测步长LSTMMLR 模型特征融合层中PM自身特征、前体特征和气象条件特征的对应模型参数。其中,“—”同表1中的“—”含义一致,表示在特征融合时舍弃了该变量。为准确反映不同变量对目标PM浓度的影响,本文在特征融合部分取消权值之和为1的约束条件,通过参数正负反映变量对目标PM浓度的积极/消极影响,通过参数在绝对值之和所占比率反映各个变量对目标PM浓度的影响,从而为后续的雾霾治理措施提供一定的参考价值。表6显示LSTM-MLR 预测步长从3h 增加至24h 时,目标PM浓度的主要影响因素及其影响力均发生了较大变化:当对PM浓度进行3h与6h的临近预测时,模型的所有输入对目标PM浓度均有促进作用;当预测步长增加至12h与24h,SO浓度变化特征与目标PM浓度变化呈负相关。SO为二次雾霾污染的主要前体,硫酸盐与可挥发有机物之间的非均相反应为雾霾爆发性增长的主要原因。原因可能是汾渭平原作为我国重要的重工业发展聚集区,煤炭消费占一次能源消费近90%,远高于京津冀和长三角地区;焦化与钢铁产业的大宗原料及产品运输80%依赖于公路运输。煤炭消费产生大量硫氧化物等,公路运输中大货车尾气排放大量氮氧化物等,二者均为雾霾污染物的前体。在雾霾重污染应急措施中,停工减产能够较快得到严格落实,而公路运输中大型货车运力控制存在滞后,导致SO浓度下降趋势早于NO浓度降低趋势,因此在模型中呈现负相关性。
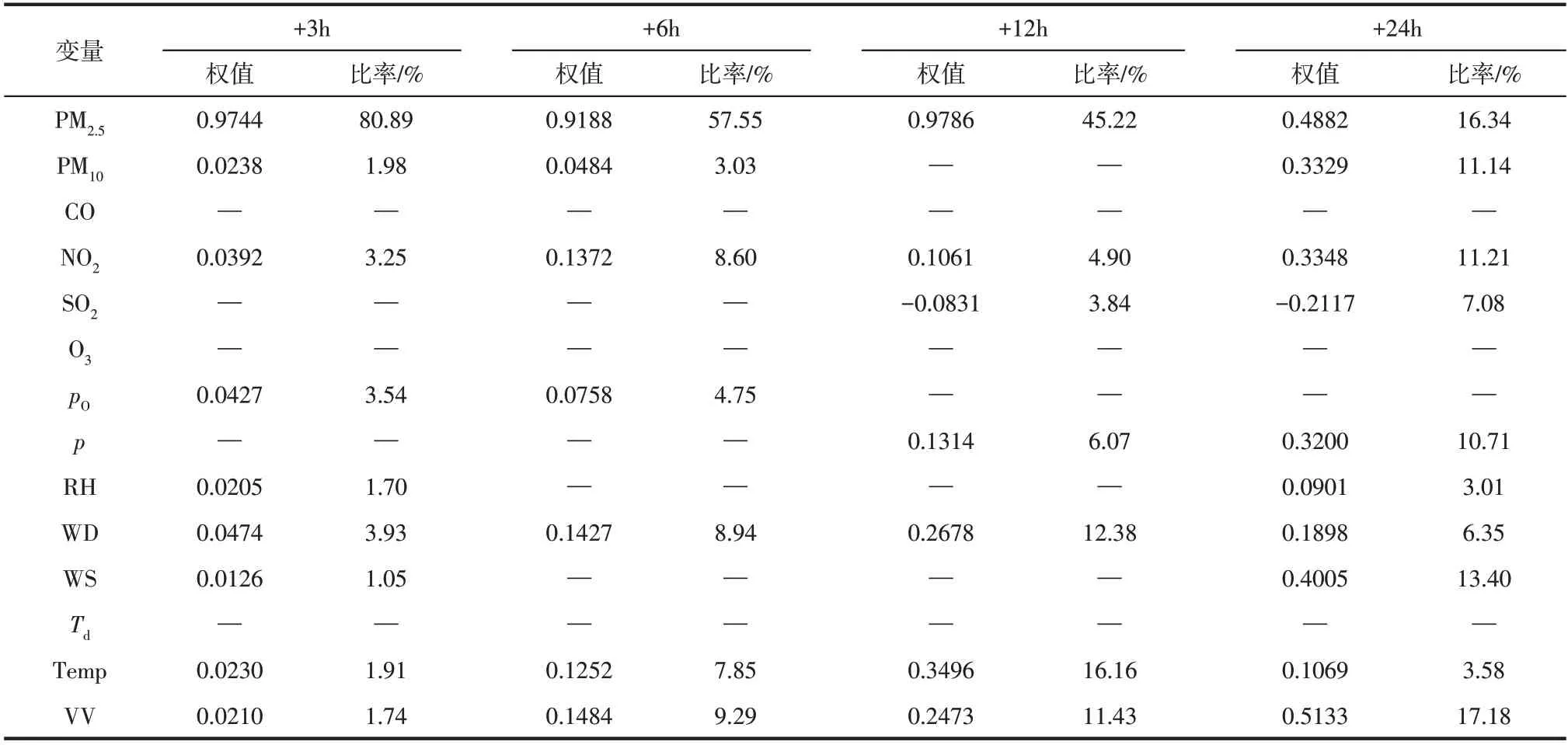
表6 不同预测步长时LSTM-MLR模型融合层参数
预测步长为3h 时,影响目标PM浓度最大的前体为NO,气象因素为风向和局部大气压;其中,前体贡献占比为5.23%,气象因子占比为13.88%,当前PM影响力高达80.89%。预测步长为6h时,前体影响力提升至11.63%,当前PM浓度影响力降低至57.55%,天气因素的影响力为前体浓度影响的2.65 倍。当预测步长提升至12h 时,SO减排的影响力开始体现,较高的高空温度形成的逆温层成为气象条件中的主导影响因素(16.16%)。预测步长为24h时,当前PM浓度的贡献率降至16.34%,前体浓度影响提高至29.43%,气象因子中的主要影响变量为局部气压、风速和可见度;各个因子贡献率的变化表明停工限产等减排措施的效果随时间变化逐渐增强,应至少提前24h开始实行。重污染过程中气象因素的影响力始终大幅度高于前体浓度的影响力,说明汾渭平原的基础排放量远高于环境容量,静稳高湿的不利天气因素容易导致二次PM生成速率大幅提高,最终造成空气重污染。
4 结论
由于汾渭平原供暖季节空气重污染发生频次高,社会影响大,本文针对重污染监测数据的多源异构性、时间序列的非平稳和多尺度特性提出了基于深度时间序列特征融合的空气重污染演变过程预测模型(LSTM-MLR)。该模型利用汾渭平原重点城市西安市的数据,通过多个不同超参数结构的LSTM 提取前体与气象因素的长时间依赖关系,利用MLR 进行特征融合实现对西安市PM浓度的临近预测,并根据融合层参数计算不同输入变量的对重污染过程中雾霾浓度的影响。结果表明,LSTMMLR 模 型 相 对RF、SVR、MLR、LSTM_PM、M_LSTM、LSTM-RF 在PM浓度预测精度及重污染预警准确率两方面均为最优。此外,相比其他模型,LSTM-MLR 兼具高预测精度和参数可解释性,即在PM重污染样本中具有最高识别准确率的同时可以量化模型输入与目标PM浓度之间的关系。
然而,LSTM-MLR 模型输入数据特征与LSTM最优超参数的关系尚未明确,输入变量无法实现长度的自适应调节。因此,匹配输入数据特征与LSTM 超参数结构,通过构建周期、趋势、步进和随机特征优化模型结构是未来的主要改进方向。

