基于位移剩余的最优货物运输服务分析

王佳彬，孙启鹏*,b，吴群琪,b，杨涵晞，马飞,b，郑颖颖，任玮

(长安大学，a.经济与管理学院；b.综合运输经济管理研究中心，西安 710064）

0 引言

供给侧结构性改革对维持货运系统高效运行具有重大影响，货物运输服务优化是供给侧结构性改革的具体化措施。然而，由于长期追求数量扩张过程中总是将运输需求作为制定规划的外生因素，运输需求简单化倾向在我国运输政策研究中已是根深蒂固，非常普遍[1]。供给侧改革的核心要义是以最恰当的运输方式，最大化地满足运输需求[2]。运输方式安排恰当与否，对运输需求的满足程度及供给侧改革的效果有决定性的影响。因此，分析市场提供的运输服务能否最大限度地满足运输需求，及其对于需求主体是否为最优选择，对于制定运输服务优化策略，供给侧结构性改革政策乃至综合运输的发展具有重大的指导意义。

市场经济是需求主导的经济。货物运输作为一种经济活动，需求主体追求自身利益最大化是其本质属性[3]。因此，“最大程度满足运输需求”等价于“需求主体利益最大化，最低限度应能满足需求主体基本利益的诉求”。分析某种运输服务能否最大程度地满足需求主体，需基于运输需求主体选择运输服务方式的机理，计算需求主体选择运输服务所产生的价值并进行比较。现有研究中关于货运服务方式选择模型主要包括：基于随机效用理论的离散选择模型、运输成本最小化模型以及基于决策论的目标优化模型[4]。例如，刘浩等[5]基于效用最大化原则，揭示不同空间特征下运输时间对效用的差异化影响。钟校等[6]在“低碳运输”背景下，构建以总运输成本最小为准则的快捷货运方式选择模型。AALOK 和RAMESH[7]采用基于决策论的Grey-DEMATEL 模型(Grey Theory and Decision-Making Trial and Evaluation Laboratory)讨论铁路多式联运服务选择问题。

效用理论将需求主体选择运输服务方式带来的满足感作为运输效用内涵[8]，即该理论将运输服务视为消费产品，假定位移需求实现后，以运输时间、运输价格、服务频率及可靠性等运输服务品质作为核心变量，测度为需求主体带来的位移价值。其核心意义在于反映需求主体在现实供给条件下完成运输服务后产生的效果。该理论有3 点值得斟酌。其一，未考虑需求的独立性和前置性。这一缺陷导致分析过程不符合运输供需关系的逻辑。货运需求主体总是基于一定的预期利益而产生运输需求[3]，因此，位移价值应为货运需求主体预期的经济利益，而采用何种运输服务实现位移属于后续决策事宜，与位移实现后给需求主体带来的满足感存在本质区别。这种认识体现这样的哲学思想：需求是具有第一性的，不因为能否实现而独立存在；运输需求主体本身存在独立的价值，是决定运输服务是否合适的前置因素。其二，该理论是在假定位移需求实现后测度位移效用，未考虑潜在运输需求。在现实供给条件下，往往会存在某些无法得到满足的运输需求，但当供给条件改善后，这些需求就有可能转化为有效运输需求。其三，计算效率问题，效用理论在位移价值的测度中，若不考虑现实技术条件约束，其函数值没有上界。因此，在寻找最佳运输服务时，随机效用理论只能通过设立全面的约束条件，用穷举法进行测算，导致计算难度较高，且计算效率较低。综上，效用理论侧重于分析需求主体在现实供给条件下完成运输服务后产生的效用大小，回答的是需求主体在现实中选择哪种运输服务最佳。本文拟解决的问题是什么样的运输服务能够最大限度地满足运输需求，使得需求主体实现最大效用。其核心在于最优供给决策分析，即分析现有技术经济条件下，使需求主体实现最大效用的运输服务。该服务可能在现实中并不存在，但完全有可能供给。由此可见，一方面，两者的内涵完全不同，而且效用理论并不具备分析该问题的理论基础；另一方面，广义运输成本最小化模型和基于决策论的目标优化模型均侧重于量化研究运输过程中的各类成本，同样，忽略了运输需求的独立性和前置性特征。

基于此，为突出强调位移需求本身具有的独立价值及其特性，本文引入位移剩余理论，以基于货运需求主体预期利益形成的位移价值与货物运输全过程的位移成本之差为货运需求主体的位移剩余，提出货运需求主体以位移剩余最大化为准则选择运输服务方式，构建位移剩余测度模型，基于现实需求条件下寻求最佳运输服务，并通过仿真算例展示模型的应用。

1 位移剩余模型的构建

为充分反应货物运输需求的独立价值，以需求主导为原则，提出位移剩余概念，认为综合运输服务方式的选择机理是：在现有的技术经济条件下，需求主体依据各运输服务的技术经济特征和其他与运输服务选择相关的决策信息，选择能够实现自身位移剩余最大化(至少是可接受)目标的综合运输服务[8]。

位移剩余为

式中：S为位移剩余；V为位移价值；C为位移成本。

位移价值V，即货物运输需求主体基于位移的预期利益。为了揭示货物运输服务方式选择的经济机理，需要分析V和C的相关特性。

1.1 位移价值V

对于货物位移需求而言，需求主体总是基于一定的预期利益产生位移需求。因此，针对于特定的需求主体和特定的市场环境，预期利益是需求主体明确认知到的，其判断往往有一定的客观依据。本文基于位移需求时效性将位移价值函数V分为3种类型：

Ⅰ类：位移价值与位移过程时间占用没有必然联系的需求。例如，矿石和建材等没有明确时间约束的位移属于这类，如图1所示。

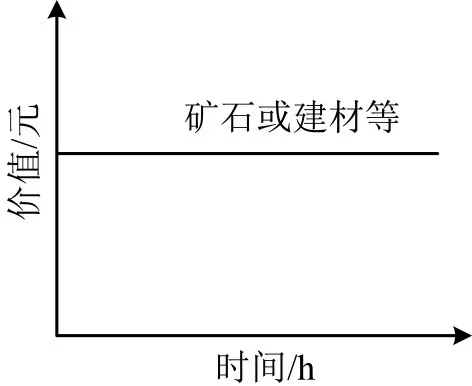
图1 Ⅰ类位移需求Fig.1 Ⅰclass movement demand

其函数表达式为

式中：VΙ(t)为位移价值函数；t为运输占用时间；A为位移价值常量，其含义为实现位移需求所预期的经济利益。

Ⅱ类：位移价值与位移过程占用时间成反比的运输需求。任何具有时效性要求的运输需求都属于这类，例如，鲜活货物的运输。如图2所示。

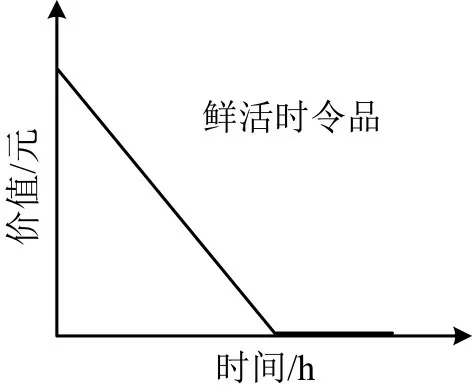
图2 Ⅱ类位移需求Fig.2 Ⅱclass movement demand

其函数表达式为

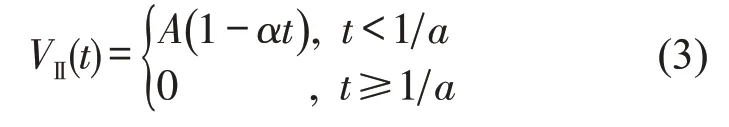
式中：α为时间敏感系数，α∈[0,+∞)。位移需求对时效性要求越高，α的值越大。当α=0 时，表示该位移需求对时间完全不敏感，其位移价值函数等同于Ⅰ类位移需求函数。

Ⅲ类：具有特定时间约束的需求。只要在特定时点完成运输，则位移价值不变，一旦超过该时点，其位移价值即为0，具有确定参展时间窗口的展品及具有保质期限的食品运输即属于此类需求，如图3所示。

图3 Ⅲ类位移需求Fig.3 Ⅲclass movement demand

其函数表达式为

式中：t0为特定约束时点。

1.2 位移成本C

位移成本是指货运需求主体为完成货物的位移，而必须付出的相关成本。位移全过程中除运价成本与时间成本外，可靠性、便捷性及安全性等运输服务品质也会一定程度上影响运输需求主体选择运输服务方式[9]。其中，可靠性成本为风险成本，包括运输过程中提前或者延迟到达导致的管理费、仓储费及缺货成本等；便捷性成本在时间成本中的服务响应时间中体现；在运输过程中对安全性的考虑可以通过保价运输等形式解决，因此，本文将安全性成本定义为主要与运输方式相关的常量C(i0)。

综上所述，第i种运输服务的位移成本Ci(t)的函数为

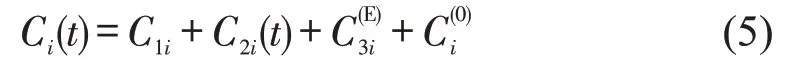
式中：C1i为第i种运输服务的运价成本；C2i(t)为第i种运输服务的时间成本；为第i种运输服务时间可靠性期望成本；为安全性成本常量。

第i种运输服务的运价成本C1i包括运输方式j的运价费用总和、转运费用和其他运杂费，其函数为

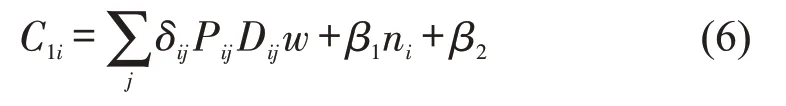
式中：j为第i种运输服务产品中的第j种运输方式；δij为哑变量，当第i种运输服务产品中的运输方式为j时，δij=1，否则δij=0；Pij为第j种运输方式的单位运价；Dij为第j种运输方式的承运里程；w为货物的重量；β1为货物转运一次的费用；ni为第i种运输服务位移全过程货物转运的次数；β2为仓储、保险及包装等运杂费。

现有研究中，普遍将时间价值(Value of Time)作为运输服务方式选择的重要变量。它主要由4部分组成：商品凝聚资金的机会成本，运输途中节约的库存成本，迟到导致的缺货成本及提前到达导致的库存成本与管理成本[10-11]。然而，提前到达或者迟到导致的相应成本属于运输过程中由于时间不可控性带来的风险成本，应归属于可靠性成本范围，需单独进行计算。因此，本文第i种运输服务的时间成本C2i包括：商品凝聚资金的机会成本和节约的库存成本Si(t)。其中，指运输过程中时间消耗导致的货物占用资金的机会成本。Si(t)为一项负成本，是在货物运输过程中所节省的库存成本。两者均为运输时间t的函数。因此，C2i与其组成部分的函数为

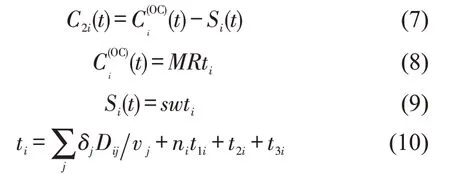
式中：M为被运送商品占用的资金额；R为单位时间资金的机会成本率；s为单位时间和单位重量的货物仓储与管理成本；ti为选择第i种运输服务方式时，货物位移全程(从联系运送直到送达目的地)占用的时间；vj为第j种运输方式的平均运营速度；t1i为转运1 次占用的单位时间数；t2i为运输需求响应的占用单位时间数，其值取决于运输方式的发车频率与运输服务质量；t3i为位移首末装卸占用的单位时间数。

运输服务方式的时间可靠性对运输需求主体的选择有显著影响[12]，尤其是对具有特定时间约束的需求，例如，JIT(Just in Time)配送服务。提前到达时段内的成本主要是货物的临时仓储成本；超时时段内主要为缺货成本。缺货带来的直接损失可用机会成本衡量，但该机会成本并不考虑某一特定货物在某一时间点对相应生产过程的重要性。例如，延迟到货可能会导致制造工厂停工[4]。因此，该位移价值损失还需考虑由于缺货带来的间接损失。综上所述，提前与超时到达的成本函数CEi和CLi为

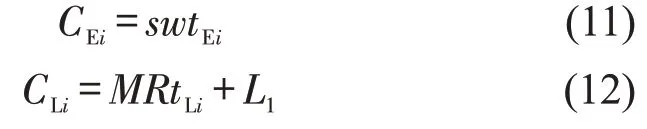
式中：tEi、tLi分别为提前、迟到的时间；L1为超时后导致的缺货间接损失。

本文在量化提前与超时到达导致的相应成本函数的基础上，将衡量时间可靠性的概率分布法与准时交付法结合[11]，计算运输时间可靠性的期望成本为

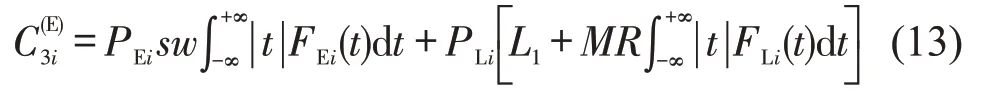
式中：PEi和PLi分别为利用准时交付法确定的第i种运输服务的提前到达概率和超时到达概率。根据现实情况，该参数的具体取值受运输方式、运输距离及中转环节次数等因素的影响[13]；FEi(t) 和FLi(t)分别为利用概率分布法确定的第i种运输服务的早到与超时时长的累计分布函数，对于这种自然呈现的“重复概率事件”[14]，可采用正态分布作为其概率分布函数。由于正态分布的期望值等于参数μ，其值可由第i种运输服务的早到与超时平均时长决定。因此，式(13)可简化为

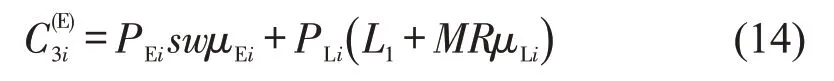
1.3 最优运输服务确定

在分析位移价值与成本并给出对应公式的基础上，本文以位移价值与位移成本之差形成货运需求主体的位移剩余，构建位移剩余测度模型。对于第k类需求主体，第i种运输服务的位移剩余为

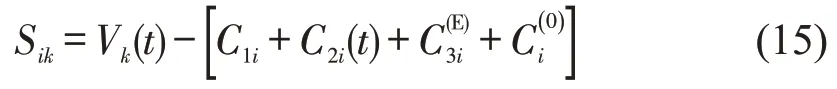
根据分析，位移成本C的值域为(0,+∞)。因此，当需求主体的位移价值函数V(t)确定时，位移剩余函数Si一定具有极大值点或者自变量定义域内的最大值点。可将位移成本C的组成部分作为位移剩余价值函数的自变量(如C1i、C2i(t)、、中具体变量)。通过求位移剩余Si的极大值或给定约束条件下的最大值，分析现有运输服务是否最优。同时，该极值点或最值点的坐标即为理论最佳运输服务方式的技术经济特征。

2 位移剩余仿真测算

2.1 仿真算例设置

为体现位移剩余理论与现有运输服务方式选择理论的差异以及确定最优运输服务的功能，假设具备以下信息的货物位移需求，测算采取不同运输服务方式的位移剩余。特别需要说明的是，本文位移价值相关参数的取值均基于经验进行赋值。虽然计算结果不具有实际指导意义，但本文试图解决的科学问题是揭示位移剩余与需求主体选择运输服务方式之间的联系，至于将相关参数设定为多少为宜，并不影响本文试图解决的科学问题。在位移价值V方面，给出3种位移价值函数，如表1所示。

表1 各类位移需求的位移价值函数Table 1 Movement value functions of various movement demands

在位移成本C方面，假设位移OD点与位移路径如图4所示，位移服务方式包括：公路直达运输、铁路多式联运(公-铁-公)、航空多式联运(公-航-公)及水路多式联运(公-水-公)。

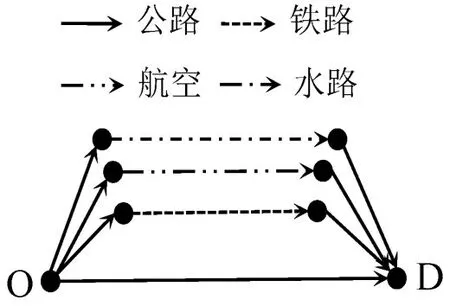
图4 各种运输服务方式路径Fig.4 Path diagram of various freight service modes

本文通过咨询相应运输单位以及参考运输行业平均水平对位移全过程具体参数进行赋值，例如，铁路运价参考国家铁路局《各类货物铁路运输基准运价率表》，不同运输方式营运速度按照运输行业平均水平设置，如表2所示。

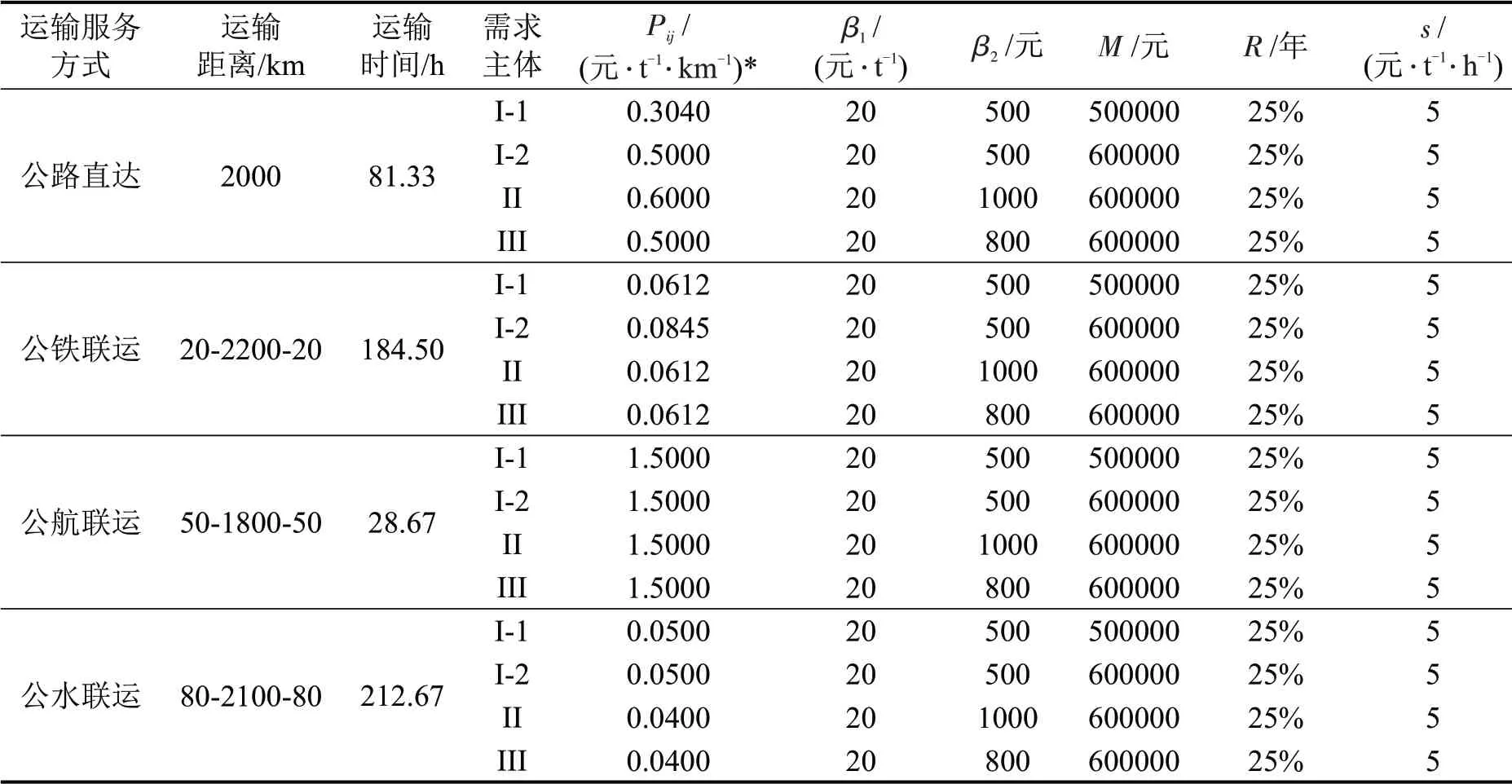
表2 位移成本相关参数Table 2 Movement cost related parameters

根据式(14)，具体参数取值以及可靠性期望成本如表3所示。

表3 I-2类可靠性成本及相关参数Table 3 Class I-2 reliability cost and related parameters

根据分析，当需求主体的位移价值函数V(t)确定时，可将位移成本C的组成部分作为位移剩余价值函数的自变量，求得位移剩余价值Si的极值与极值点，分析最优运输服务方式。为便于展示，本文仅选定在途运输时间t0i与需求响应时间t2i为运输服务方式的品质变量，并假定t0i和t2i与单位运价Pi之间的关系式为

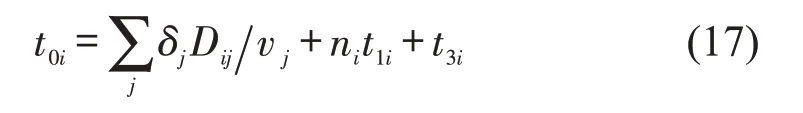
式中：Pi为第i种运输服务的单位运价；t0i为在途运输时间，包括：途中运输时间、途中转运时间t1i与首末站装卸时间t3i。

2.2 仿真算例结果与分析

根据仿真算例的参数设置，带入式(5)～式(15)，计算位移剩余Sik，如表4所示。

表4 各种运输服务方式的位移剩余价值SikTable 4 Movement surplus of various freight service modes (元)

算例结果表明：根据位移剩余最大化准则，对于I-1、I-2、II 及III 类位移需求，需求主体将对应选择的运输服务方式分别为公铁联运、公铁联运、公路直达及公航联运的运输服务方式。为观察各个参数变量对位移剩余的影响程度，本文以I-1 需求为例，进行参数敏感性分析，如图5所示。

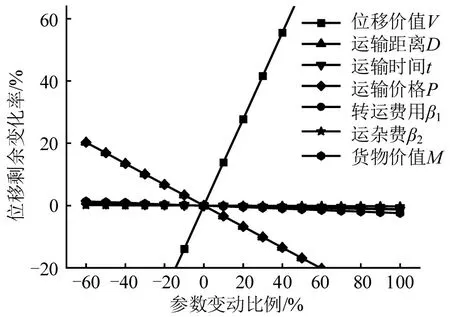
图5 参数敏感性分析Fig.5 Parameter sensitivity analysis

根据图5可知，各参数在相同变化幅度情况下，位移价值V对于位移剩余的变化率影响最大，其次为运输距离D与运输时间t，其余相应位移成本参数变化幅度相似。由此说明，位移价值对于货运需求主体选择运输服务方式的影响最为显著，是进行货运服务优化时重点关注的要素。

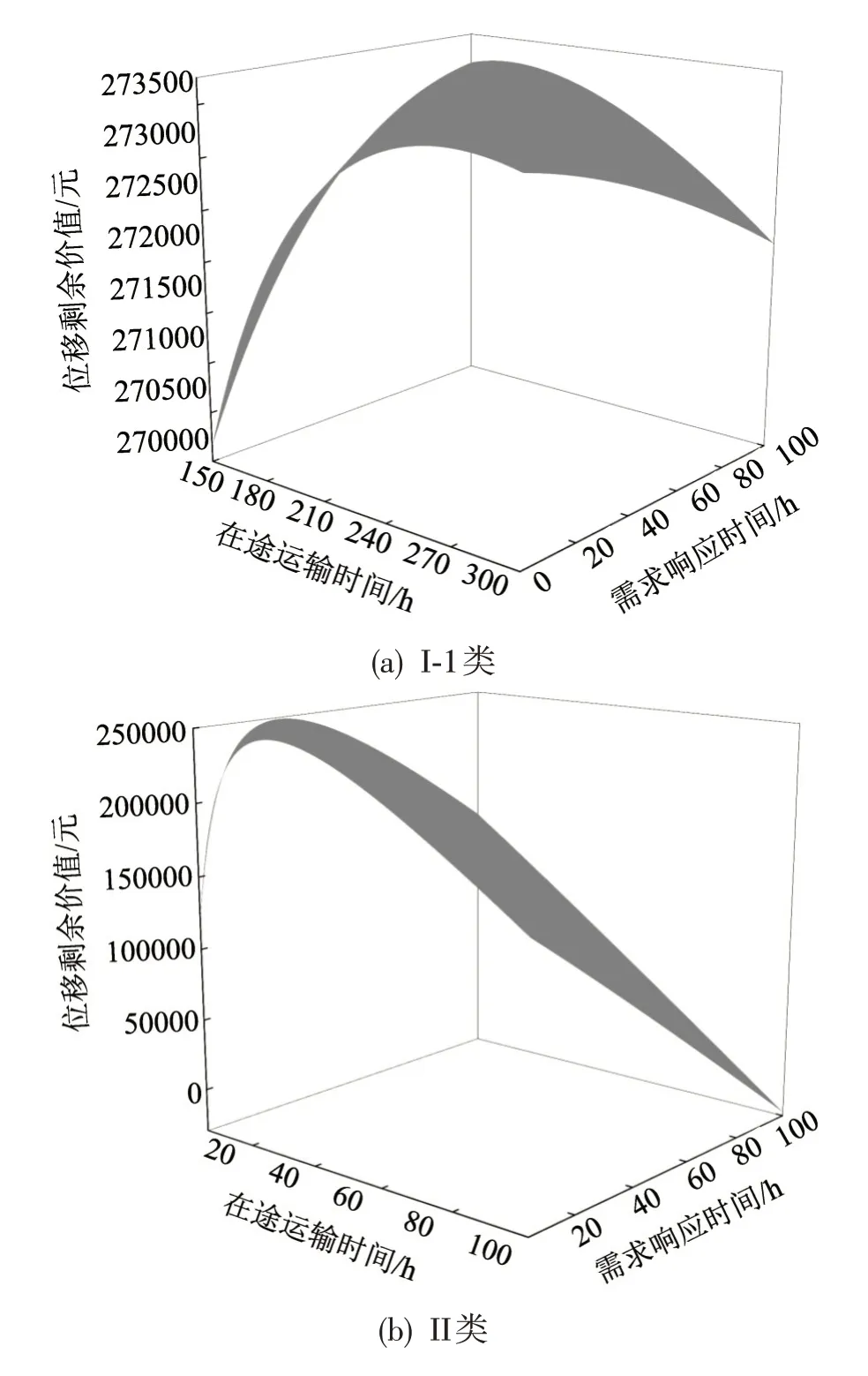
同时，在假设其他参数给定的情况下，将式(16)带入位移剩余模型，求得I-1、II及III类位移剩余曲线，如图6所示。

由图6可知，对于I-1类需求主体，当t0i+t2i=271，P=0.038 时，位移剩余曲线存在极大值S=273505.8；对于II 类需求主体，当t0i+t2i=35.2，P=0.3 时，位移剩余曲线存在极大值S=248901.73；对于III 类需求主体，在其时间约束范围内，位移剩余曲线没有极大值点，当t0i+t2i=80，P=0.13 时，曲线存在最大值S=357856。

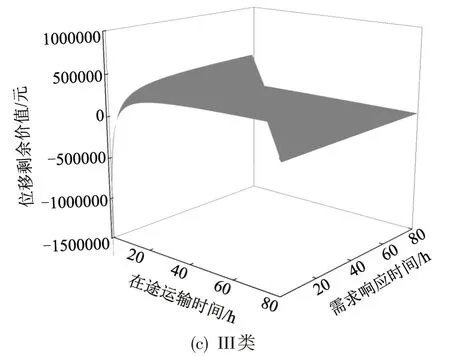
图6 I-1、II及III类位移剩余曲线Fig.6 Movement surplus curves of classes I-1,II and III

以I-1类需求主体为例，根据设置的仿真算例，现有的4种货运服务方式中，位移需求主体选择铁路多式联运(t0i+t2i=184，P=0.06，S=260930.34)的位移剩余最大。但是，根据式(17)得出的I-1需求主体理论最大剩余价值为S=273505.8，对应的最佳运输服务方式的参数为t0i+t2i=271，P=0.038。不难看出，其更接近于水路多式联运的技术经济特征。根据本文仿真算例的设定，现有水路多式联运运输服务参数为t0i+t2i=212.67，P=0.05，S=257671.23。若将该运输服务进行优化，提升运输时间，降低运输成本，可以最大程度地满足I-1类需求主体。对于II类需求主体，当时间敏感系数α=0 时，即需求主体对时间完全不敏感，其极值点与I-1 类需求主体相同。随着α的增加，其位移剩余曲线的极大值点会向左下方偏移。根据本文对II 类需求的设定，当α≥0.038 时，位移剩余函数极大值Smax≤0，此时，不存在最优运输服务方式。对应现实中类如新鲜松茸的运输，由于其变质速度过快，如若不对货物进行保鲜处理，使得时间敏感系数α降低至一定数值，将无法进行长距离运输。这也充分说明，当供给条件有所改善后，一些潜在运输需求可以转化为有效运输需求。综上，本文设置的位移剩余模型可根据异质性的位移需求，分析现有运输方式是否最优，以及得出最优运输服务的相关品质要素，同时，可以考虑潜在运输需求，分析其转化为有效运输需求的条件。

3 结论

本文将位移价值和位移成本作为测度位移剩余的两个独立变量，构建最优运输服务分析模型。通过特定条件下的仿真算例验证，得出以下结论：基于货运需求主体预期的经济利益构建位移价值函数，体现了需求主导的思想，强调了需求本身具有的独立价值，避免了随机效用等理论在位移价值测度的表述局限。构建的基于位移剩余的最优运输服务分析模型，充分考虑了需求异质性的特点，可根据不同的位移需求分析现有运输服务是否最优，并可以分析潜在运输需求转化为有效需求的条件，为运输服务优化提供参考标准；符合需求主体实际选择运输服务方式的逻辑，可为企业以及政府制定运输供给优化策略提供决策参考依据。