基于混沌吸引子的真空断路器永磁斥力机构机械故障识别方法
刘晓明 张煦松 姜文涛 陈 海 陈军平 宋柏阳
基于混沌吸引子的真空断路器永磁斥力机构机械故障识别方法
刘晓明1张煦松1姜文涛2陈 海1陈军平3宋柏阳1
(1. 省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学) 天津 300130 2. 天津工业大学机械工程学院 天津 300387 3. 成都旭光电子股份有限公司 成都 610500)
针对真空断路器斥力机构故障时振动信号瞬态、非线性且难以进行故障定量评估与识别的问题,该文提出一种基于吸引子形态的混沌吸引子矩特征量和粒子群优化支持向量机的斥力机构故障评估与识别方法。以斥力机构分合闸过程中典型故障,特别是分闸油压缓冲器不同过调故障程度的振动信号为分析对象,首先采用混沌理论相空间重构方法和Wolf算法,得到最大Lyapunov指数,表明斥力机构振动信号具有明显的混沌特性,通过三维相图定性分析振动信号混沌吸引子演变规律;然后引入混沌吸引子矩理论,提取四种二维吸引子矩,利用最小二乘法线性回归计算第一区域曲线斜率为吸引子形态特征量,同时提取时域信号共同组成特征向量库;最后比对分析支持向量机算法与粒子群优化-支持向量机组合算法的准确率。实验结果表明,文中所用方法可精准识别斥力机构故障类型。
真空断路器 斥力机构 油压缓冲器 吸引子形态 支持向量机
0 引言
真空断路器作为电力系统的控制与保护电气设备,其运行特性是影响系统安全可靠运维的主要因素之一[1]。据统计,在真空断路器服役过程中,机械故障占其整机故障的80%左右[2-3],对真空断路器运行故障进行评估与识别,具有理论和工程意义。
断路器分、合闸动作产生的振动信号蕴含着丰富、重要的机构状态信息,是机构运动过程中是否出现铁心卡顿、铁心与斥力盘松动、油压缓冲器过调等“故障集总”参数。断路器中的油压缓冲器可吸收机构分闸运动末期的剩余能量,用以减少冲击与振动,在真空断路器中扮演着不可或缺的角色[4]。此外,油压缓冲器也直接影响斥力机构分闸行程末端反弹幅值大小或弹跳时间长短:一方面,过大反弹幅值或过长弹跳时间将不可避免地导致灭弧室波纹管承受大振幅强迫振动而引发波纹管开裂进而造成灭弧室漏气;另一方面,过大分闸反弹幅值使动静触头间有效开距严重减小,灭弧室在开断过程中无法达到安全间隙,导致灭弧室重击穿,造成分闸失败。基于上述分析,利用振动信号对断路器的机械运行状态,特别是油压缓冲器的故障类型进行识别十分必要。
断路器开断过程中振动信号具有瞬态、非线性和非平稳的特点。国内外学者从信号采集、特征提取与故障识别等方面进行了大量的研究[5]。特征提取通常采用时域法、频域法、时频法、数据序列法或者几种方法的组合。随着人工智能算法的发展,神经网络、小波包分解与支持向量机(Support Vector Machine, SVM)等算法被引入故障识别。文献[6]将断路器的振动信号进行经验模态分解,代入本征模态函数,将边际谱能量作为特征向量,利用决策表规则进行神经网络预测。文献[7]对振动信号进行变分模态分解,采用短时能熵比的双门限法进行时域检测。文献[8]采用小波包能量特征熵对断路器振动信号进行故障诊断。文献[9]基于小波包分解、希尔伯特-黄变换提取振动信号能量熵向量,应用SVM进行故障诊断。文献[10]将振动信号经小波变换转换成时频谱图,提取纹理特征和形状特征为特征向量,利用SVM实现分闸缓冲器状态的识别。上述研究多基于断路器的弹簧机构和液压机构等,随着直流电网的发展,提升直流断路器故障分断能力变得愈发重要,基于电磁斥力机构的快速真空断路器作为直流开断模块的主开关已经成为共识[11]。
本文以真空断路器永磁斥力机构为研究对象,斥力机构为分合闸提供动力,相比于弹簧机构、气动液压等机构,斥力机构具有响应及时、速度快、部件少和精度高等优点[12-13],但其速度快、冲击力大、弹跳大与动态参数多,且永磁斥力机构动作时间只有十几、甚至几个毫秒,其振动信号更加复杂、非线性程度更加明显,基于传统时间序列的振动分析变得更为复杂。
将相空间重构引入断路器振动信号分析,可有效通过吸引子的演化规律分辨故障类型或故障程度。文献[14]提出将混沌理论中的相空间重构引入振动信号分析,采用关联维数分析机构机械状态与机构运行状态。文献[15]针对高压断路器振动信号采用功率谱和Lyapunov指数进行混沌分析,探究了不同故障程度下的混沌吸引子演变规律。文献[16]根据断路器动作时序将振动信号分时分割处理,将分时信号各模态分量自适应分离,利用重构模态分量的混沌吸引子形态判断各零部件不同故障严重程度。上述文献研究表明,混沌吸引子方法可有效判断故障类型,而针对快速永磁斥力机构的振动信号吸引子形态的研究需进一步提取特征向量,完成故障的评估与分类。
基于上述分析,以真空断路器永磁斥力机构为研究对象,基于混沌理论对机构分合闸卡顿、斥力机构操作功不是引起的分/合闸不到位、合闸反弹和分闸过程油压缓冲器过调等故障类型进行相空间重构,运用C-C算法计算延迟时间和嵌入维数,采用Wolf算法得出最大Lyapunov指数(max)判断振动信号的混沌特性,通过相图定性分析其三维混沌吸引子演变规律;引入混沌吸引子矩理论,以振动信号二维吸引子相图为对象,计算主轴、副轴、原点和混合吸引子矩,运用最小二乘法做线性回归得出的吸引子形态特征量为特征向量,同时提取时域信号的均值和均差值共同组成特征向量库;应用粒子群优化(Particle Swarm Optimization, PSO)算法对SVM的惩罚系数和核函数半径优化,进而实现不同故障类型的评估与识别,技术路线如图1所示。
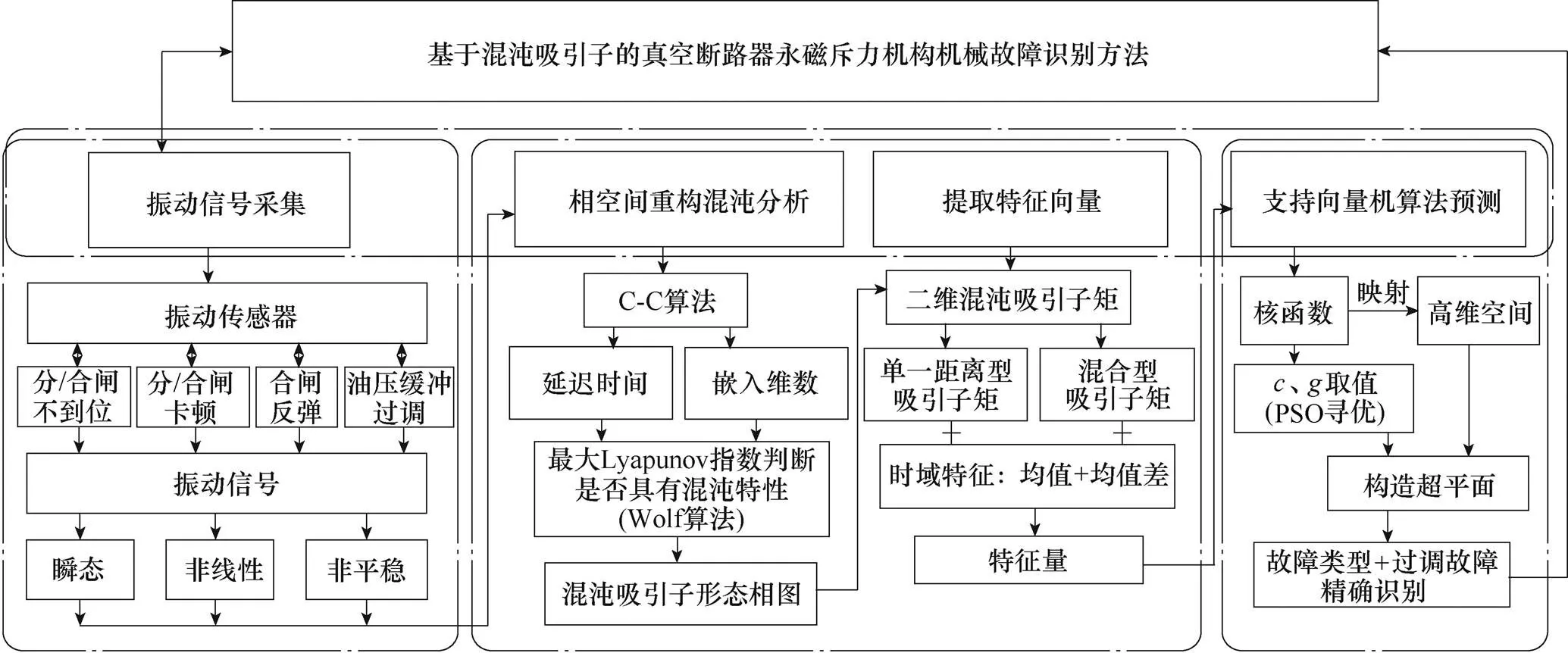
图1 技术路线
1 分合闸振动信号采集
本文以400V/400A/25kA真空断路器斥力机构为研究对象,分闸采用油压缓冲器吸收冲击能量,振动传感器和油压缓冲器的安装位置如图2所示,机构最佳缓冲间隙3.0mm,行程5.5mm,缓冲间隙值是反映油压缓冲器过调故障表征量,1.5~3.0mm的缓冲间隙反映了油压缓冲器的过紧程度,原因是缓冲器预紧量难以调试,3.0~5.0mm的缓冲间隙为油压缓冲器松动程度,原因是安装调试出错或者断路器长期工作中老化松动。同时,对由于操作功不是造成的斥力机构分/合闸不到位的振动信号以及分合闸卡顿和合闸反弹等典型故障的振动信号进行采集。
分闸缓冲间隙不同振动信号明显不同,典型条件下振动信号如图3所示,图3a~图3h为油压缓冲器在缓冲间隙1.5~5.0mm变化的时振动信号。分析表明,图3d为油压缓冲器在最优固定位置时的振动信号。
对比图3a~图3c可知,伴随油压缓冲间隙减小,过紧程度增加,振动信号幅值渐增且杂乱程度增加。

图2 斥力机构振动传感器与缓冲器安装位置
缓冲间隙1.5mm时(见图3a),运动末期出现第二个信号波,油压缓冲器无法完全吸收机构运动末期冲击能量,导致斥力机构分闸过程中出现反弹,严重时甚至导致分闸动作失败。
对比图3e~图3i可知,伴随缓冲间隙增加,缓冲器逐渐松动或者漏油时,缓冲有效距离变短,斥力机构末期的冲击能量未被吸收,碰撞力增加、冲击变大,运动后期小波明显增加。

图3 典型条件下振动信号
分析图3g与图3i可知,油压缓冲器几乎失效,振动信号波形幅值与杂波明显增加。
分析图3j与图3l可知,当机构运动过程中发生卡顿故障时,振动信号波峰明显增加且出现第二个信号波。
图3m、图3n相比于图3d、图3k,当斥力线圈操作功不足,机构分/合闸不到位,所产生的故障振动信号幅值小。
图3o相比于图3k,当机构合闸运动末端发生反弹时,运动前期振动信号波峰明显增加,运动末期出现第二个信号波,呈现反弹现象。
2 斥力机构振动信号混沌分析
斥力机构振动信号为典型瞬态非线性信号,传统的单独提取时频域特征向量方法不再适用。对于复杂非线性系统,选取一个或几个参数时间序列间接计算和判定max,通过该表征混沌的特征量来判定振动信号混沌行为。采用计算max对直流真空断路器永磁斥力机构振动信号进行混沌态研究分析,利用相空间重构、C-C及Wolf算法计算max,判断振动信号混沌态,构造三维相图分析不同故障类型下振动信号混沌吸引子形态演化规律。
2.1 振动信号相空间重构法
1)相空间重构

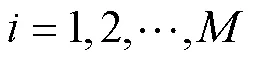
2)C-C算法

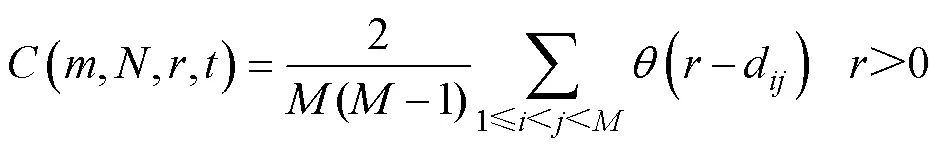
其中
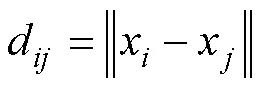
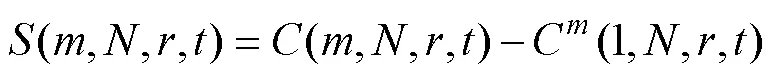
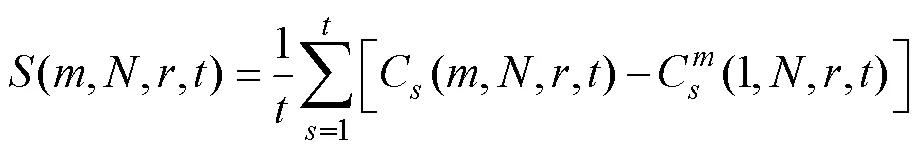
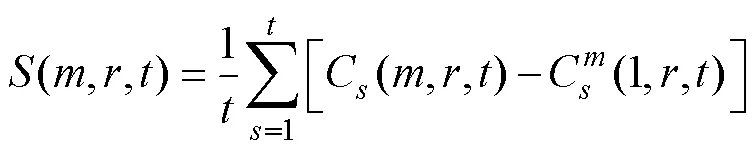
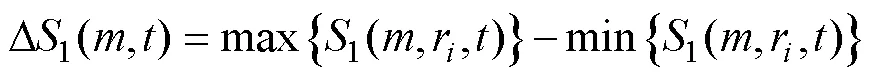

3)Wolf算法
max是表征系统混沌特性的重要特征量,Wolf算法利用高维相空间中相轨线、相面积和相体积等的演化来计算。以真空断路器斥力机构振动信号为时间序列求解max的Wolf算法实施路线:
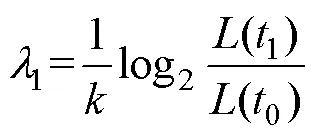
反复遍历所有相点,对系统各线度指数增长率取平均值为max估计值,有
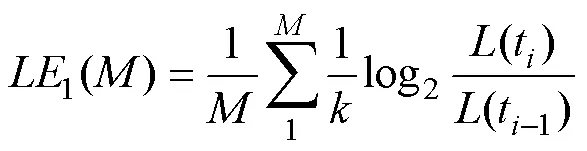
将嵌入维数逐渐增加,重复上述步骤,至Lyapunov指数数值和嵌入维数变化平稳时,求得max。
2.2 振动信号混沌判断
最大Lyapunov指数见表1。针对不同故障类型与程度得到的振动信号max,max均大于0,表明真空断路器斥力机构在不同故障类型下的振动信号具有混沌特性。1.5~2.5mm和3.5~5.5mm的max呈递增趋势,并且当卡顿故障和合闸反弹发生时,max明显变大,表明真空断路器斥力机构发生机械故障时,振动信号的混沌特性更加明显,随着故障严重程度增加,max呈现逐渐增加的演化规律。
表1 最大Lyapunov指数
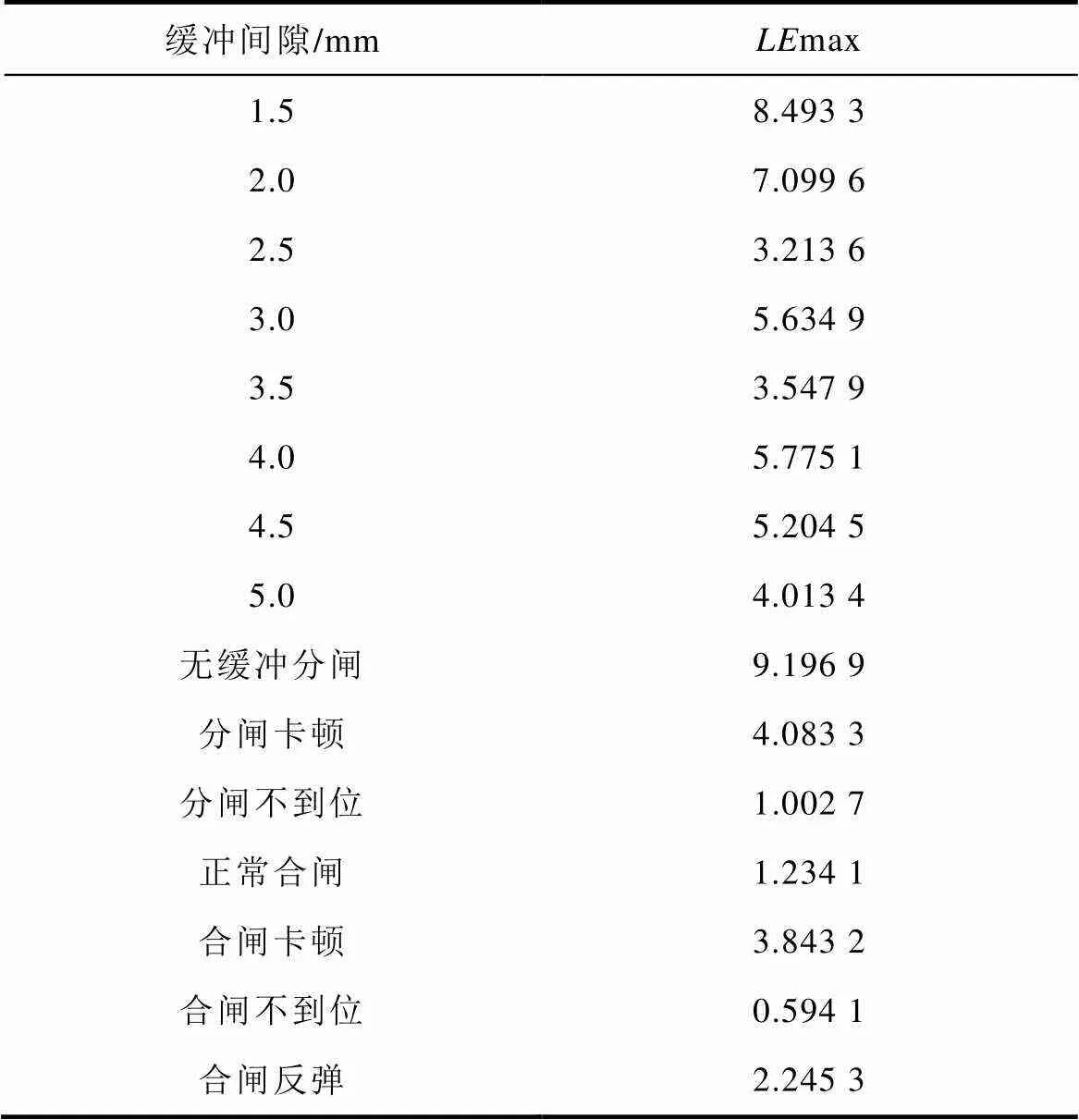
Tab.1 The largest Lyapunov exponents (LEmax)
2.3 振动信号混沌吸引子形态
构建三维相图分析混沌吸引子演化规律,典型条件下振动信号三维吸引子形态如图4所示。图4a~图4h分别为油压缓冲器缓冲间隙变化1.5~5.0mm。吸引子以原点为中心交织在一起,具有明显的混沌特征。
分闸油压缓冲器最优位置时的振动信号混沌相图如图4d所示,吸引子轨迹聚拢在空间原点附近,相较于其他情况时吸引子轨迹杂乱度较小,表明油压缓冲器能够有效吸收机构运动末期剩余能量,起到了减少冲击和防止弹跳作用。
图4a~图4c为缓冲器过紧时吸引子形态,伴随缓冲间隙逐渐减小,吸引子逐渐“远离”空间原点,杂乱程度明显增加。
图4e~图4i为缓冲器松动程度逐渐增加直至完全失效这一过程吸引子形态变化,随着缓冲器吸收剩余能量减少,吸引子同样“远离”空间原点,无法起到减少弹跳和振动作用。
通过图4j、图4d和图4k、图4l两两比对可知,当斥力机构发生卡顿现象时,吸引子轨迹更加复杂、杂乱程度增加。
图4m、图4n相比于图4d、图4k可知,当斥力线圈操作功不足,机构分/合闸不到位,吸引子杂乱程度低。
图4k与图4o对比可知,机构合闸末端发生反弹故障时,吸引子“远离”空间原点程度增加,杂乱程度高。

图4 典型条件下振动信号三维吸引子形态
相空间中混沌吸引子形态是判断断路器机构运动状态的重要依据,振动信号的复杂性、非线性需研究高维空间下吸引子形态学特征,但由于高维空间下观察吸引子轨线为定性分析,定量判断机构运动混沌规律十分困难,故文中将一维时间序列映射到二维相空间,引入吸引子矩定义,提取二维相空间特征量,即可定量描述系统混沌特性。
构建二维相空间吸引子形态如图5所示,图5a~图5h分别为油压缓冲器缓冲间隙变化1.5~5.0mm。由图可知,吸引子形态演化规律与图4所示三维相空间吸引子轨迹规律基本一致,表明二维相空间同样可准确反映系统信息。
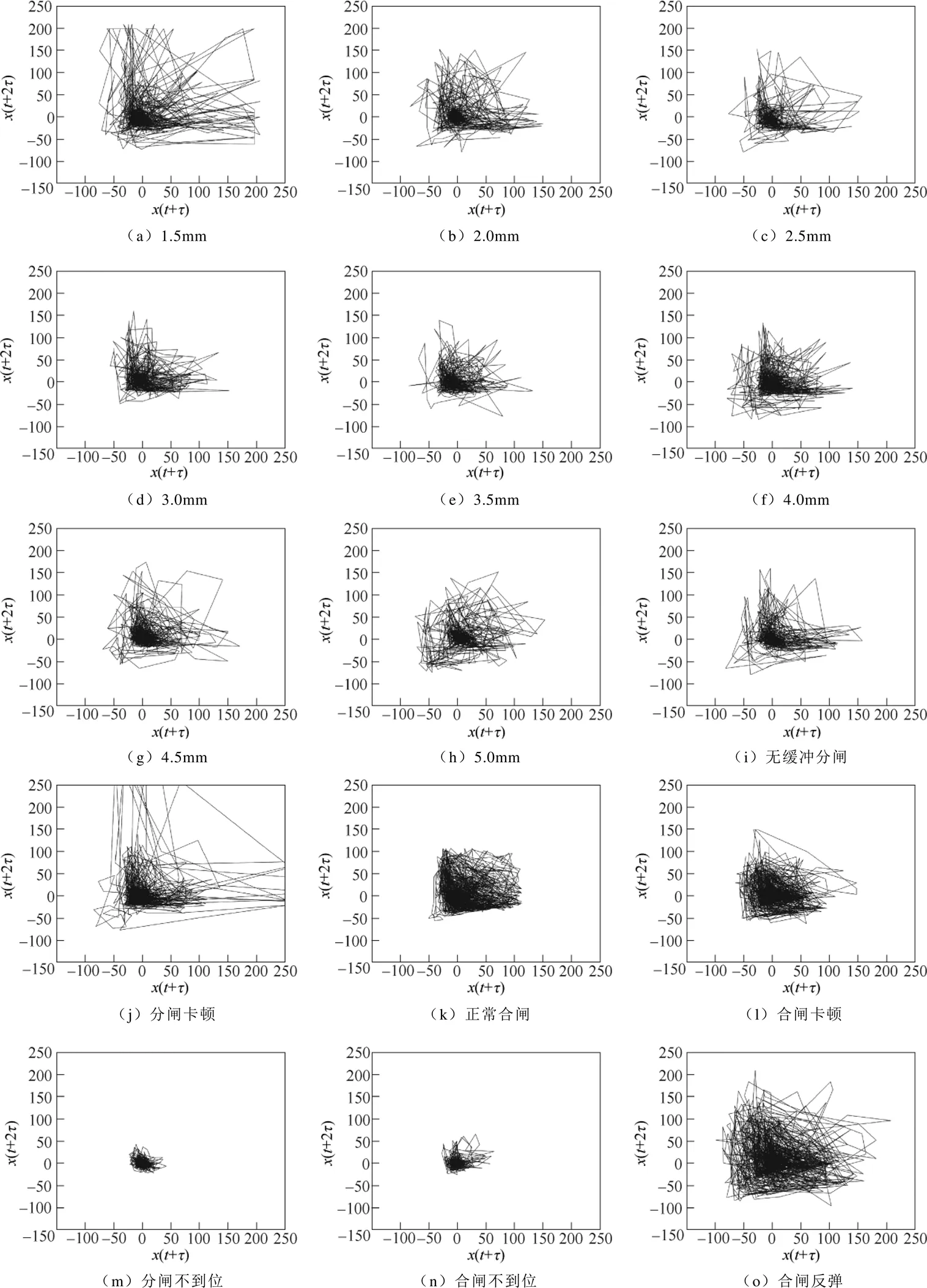
图5 典型条件下振动信号二维吸引子形态
3 特征向量提取
3.1 混沌吸引子矩的定义

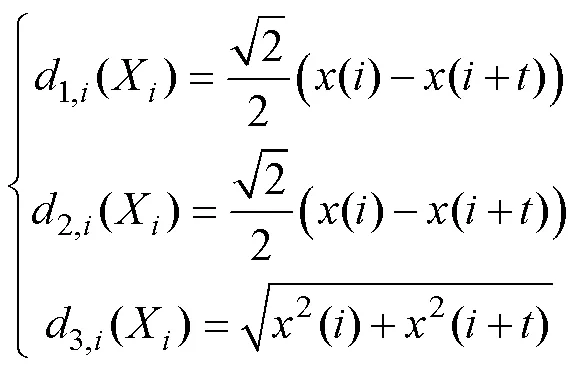
对于三种单一距离型吸引子定义吸引子矩为
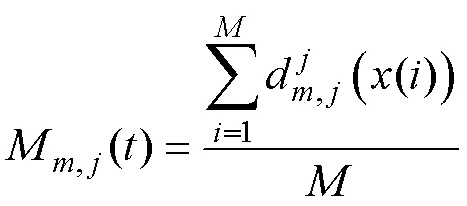
混合型吸引子矩为

3.2 吸引子特征量提取

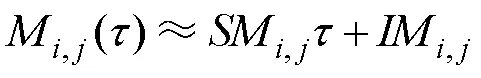
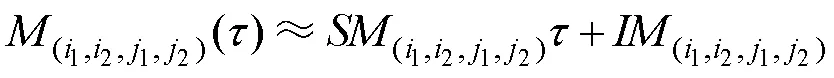

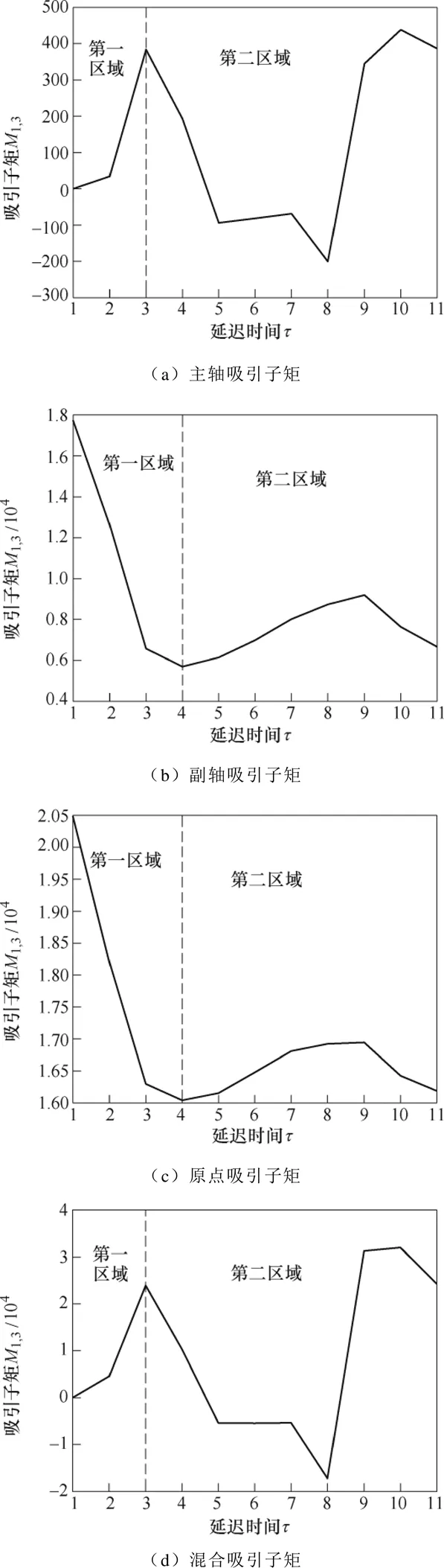
图6 吸引子矩
针对斥力机构故障类型与油压缓冲过调程度,基于混沌吸引子矩求得吸引子形态特征量见表2。吸引子特征量与机构运动过程故障严重程度有关,且随着斥力机构故障严重程度的增加,吸引子特征量整体呈现增大趋势,当合闸反弹和卡顿故障发生时,吸引子形态特征量明显增加。
3.3 振动信号时域特征提取
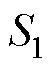

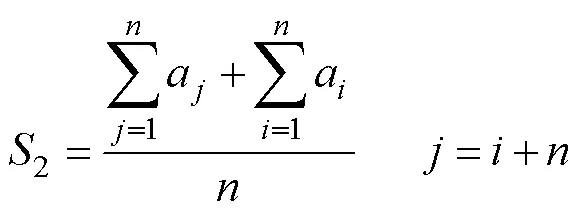
表2 吸引子形态特征量
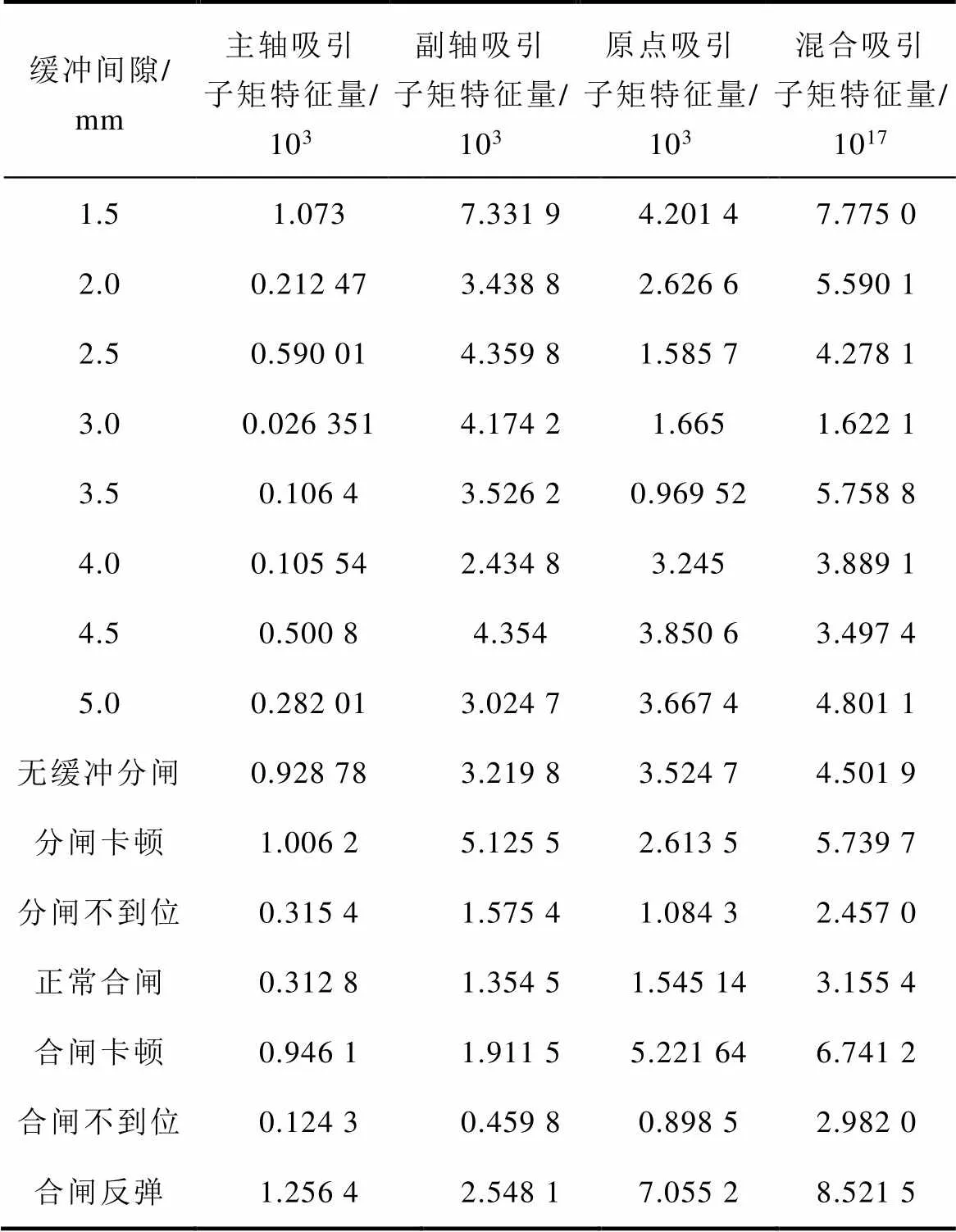
Tab.2 Attractor morphological characteristic quantity
振动信号采集系统采样频率为100kHz,采样时间60ms,记录长度为100 000kHz×0.065=6 000,每个时间窗口数据长度为5。斥力机构动作时间为十几ms,0~12ms机构未动作,时域信号无变化,故选取18~30ms内加速度均值和均差值为时域特征向量,振动信号时域特征如图7所示。由图7可知,随着合闸反弹和分合闸卡顿故障发生或故障程度增加,时域信号均值和均差值均呈现增大趋势。
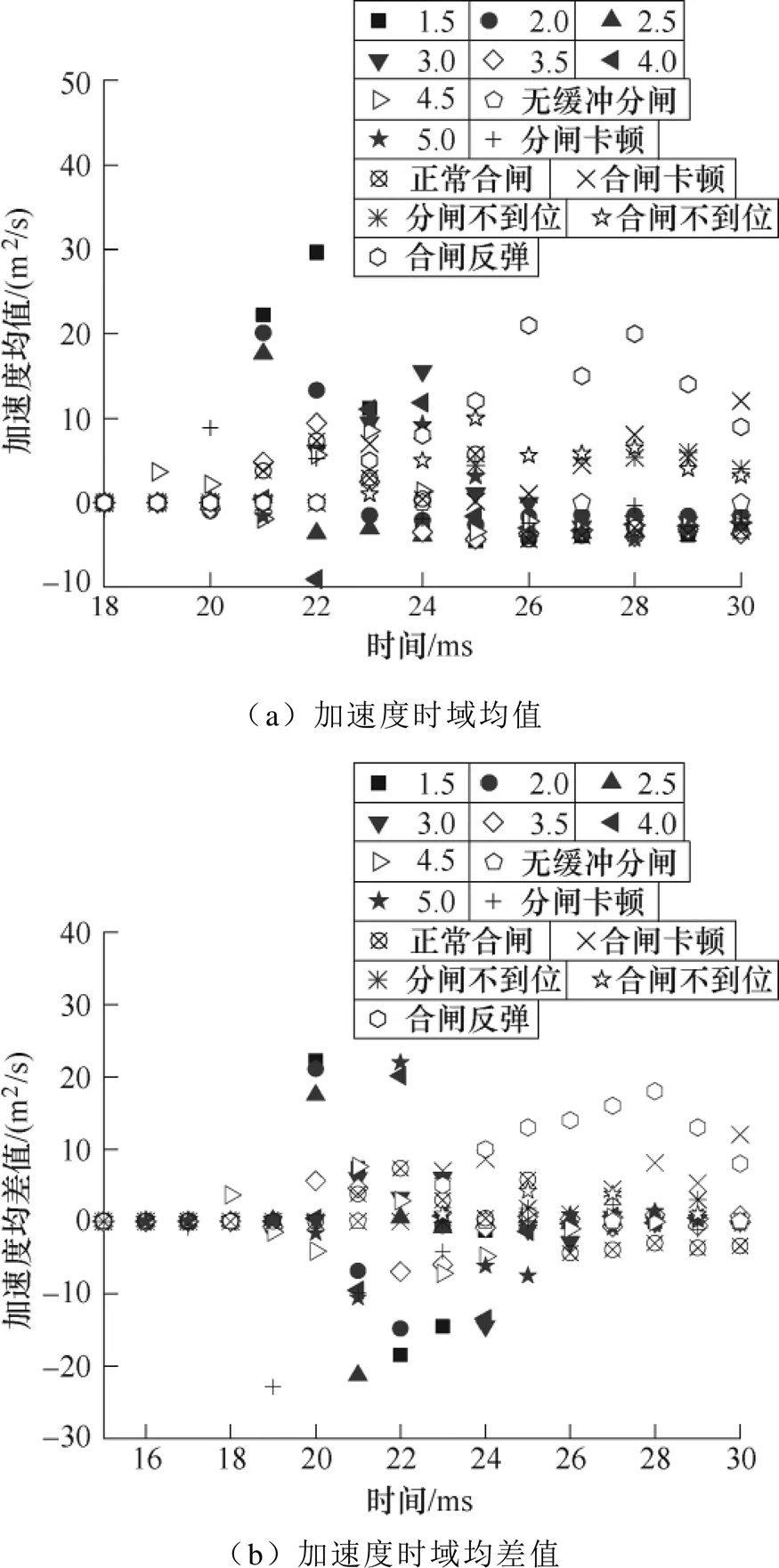
图7 振动信号时域特征
4 结果分析
依据油压缓冲器不同故障严重程度和故障类型将斥力机构机械状态进行分类,见表3,共分为15种状态类型。
表3 机械状态分类
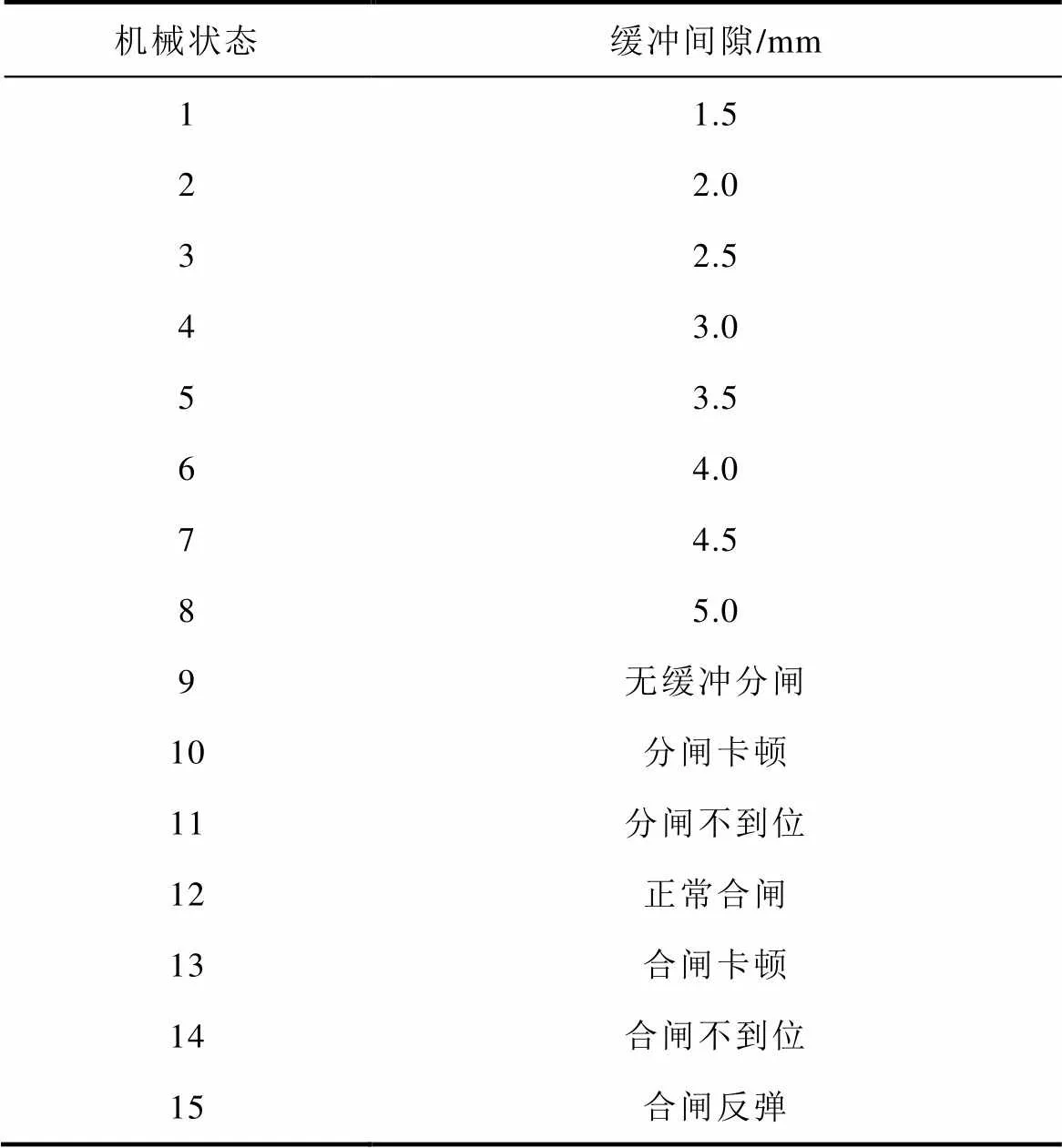
Tab.3 Classification of mechanical state
4.1 数据分类
针对15种不同断路器机械状态,每种状态采集10组,共150组数据;每种状态选取8组数据,共120组数据作为训练样本;其余30组数据作为测试样本,用于验证分类效果,分类标签见表4。
表4 分类标签

Tab.4 Classified labels
4.2 支持向量机分类识别
根据实验采集得到的斥力机构振动信号往往为有限数据,属于小样本情况。SVM通过核函数将非线性的测试与预测样本映射到高维空间,构造超平面进行分类,在处理小样本数据方面有着独特优 势[20-21]。选取广泛应用的径向基函数(RBF Radial Basis Function)核函数,其具有映射维度广、需确定参数少和泛化性能好等优点。
图8为采用传统SVM进行分类测试的识别结果,准确率为96.67%,原因除了断路器振动信号采集误差,惩罚参数与核参数的选取也是重要影响因素之一。传统SVM对于、的选取为试算法,存在算法误差和初始值选取误差。
为减少、选取带来的误差,选取和作为优化变量,运用PSO进行优化,优化流程如图9所示,计算适应值,种群迭代,寻求最优参数。
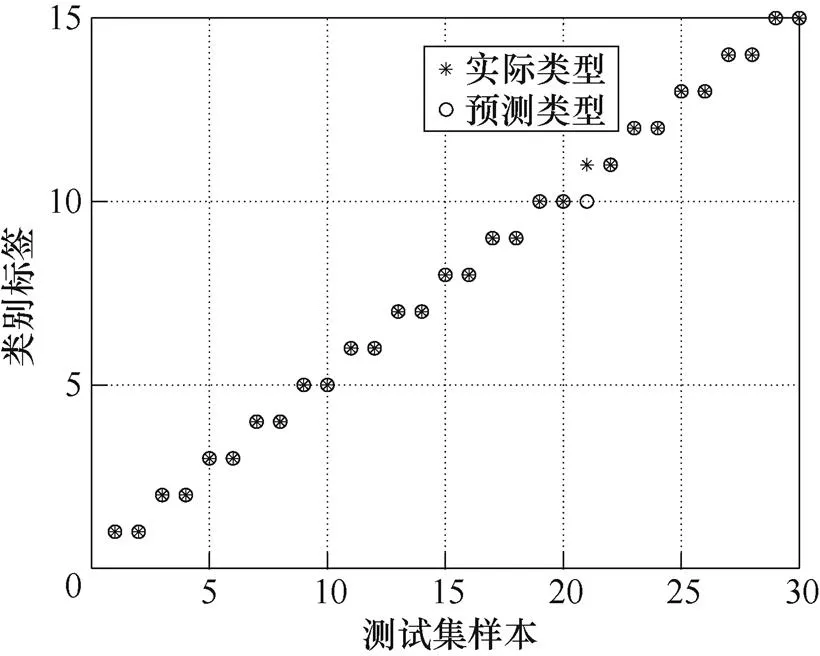
图8 SVM识别结果

图9 PSO-SVM流程
选取=1.5与=1.7作为优化变量初始值,优化结果为=7.281 2与=0.01,PSO-SVM识别结果如图10所示,准确率达100%。表明本方法可精准识别断路器斥力机构故障类型和故障严重程度。
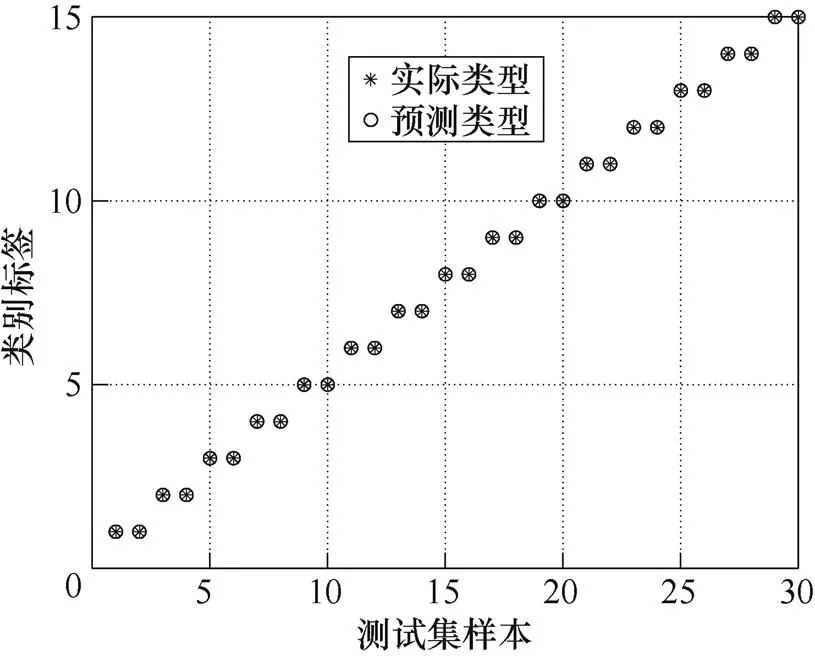
图10 PSO-SVM识别结果
5 结论
以真空断路器永磁斥力机构为研究对象,以机构分合闸卡顿、操作功不足引起的斥力机构分/合闸不到位、合闸反弹、分闸过程油压缓冲器不同过调故障类型的振动信号为分析对象,采用混沌理论的相空间重构法,得到max值均大于0,表明斥力机构振动信号具有明显混沌特性。
通过三维相图定性分析混沌吸引子演变规律,当斥力机构发生卡顿、反弹或者随着故障严重程度增加,振动信号吸引子轨迹更加复杂、杂乱程度增加。
引入混沌吸引子矩理论,通过构造振动信号二维吸引子相图,计算主轴、副轴、原点和混合吸引子矩,运用最小二乘法线性回归求解第一区域曲线斜率作为吸引子形态特征量,同时提取时域信号均值与均差值作为特征向量。
基于吸引子形态特征量、时域信号均值与均差值组成的特征向量数据库,采用SVM对样本进行分类识别,准确率达96.67%,运用PSO对SVM的惩罚系数和核函数半径进行优化,运用PSO- SVM进行故障识别,结果准确率达100%。实验结果表明,文中所用方法可精确识别斥力机构故障类型与程度,为断路器机械故障评估与识别提供了新思路与新方法。
[1] 刘路辉, 叶志浩, 付立军, 等. 快速直流断路器研究现状与展望[J]. 中国电机工程学报, 2017, 37(4): 966-977.
Liu Luhui, Ye Zhihao, Fu Lijun, et al. Research & development status and prospects of fast DC circuit breakers[J]. Proceedings of the CSEE, 2017, 37(4): 966-977.
[2] 杜凌艳, 王振浩, 王刚, 等. 高压断路器运行状态实时监测系统设计[J]. 电力自动化设备, 2006, 26(1): 58-61.
Du Lingyan, Wang Zhenhao, Wang Gang, et al. Design of real-time operating state monitoring system for HV breaker[J]. Electric Power Automation Equipment, 2006, 26(1): 58-61.
[3] 王灿, 杜船, 徐杰雄. 中高压直流断路器拓扑综述[J]. 电力系统自动化, 2020, 44(9): 187-199.
Wang Can, Du Chuan, Xu Jiexiong. Review of topologies for medium-and high-voltage DC circuit breaker[J]. Automation of Electric Power Systems, 2020, 44(9): 187-199.
[4] 马曾锐, 赵伟涛. 弹簧操动机构分闸缓冲性能研究与优化[J]. 高压电器, 2017, 53(1): 138-143, 150.
Ma Zengrui, Zhao Weitao. Research and optimization on the opening cushion performance of spring operating mechanism[J]. High Voltage Apparatus, 2017, 53(1): 138-143, 150.
[5] 常广, 张振乾, 王毅. 高压断路器机械故障振动诊断综述[J]. 高压电器, 2011, 47(8): 85-90.
Chang Guang, Zhang Zhenqian, Wang Yi. Review on mechanical fault diagnosis of high-voltage circuit breakers based on vibration diagnosis[J]. High Voltage Apparatus, 2011, 47(8): 85-90.
[6] 林琳, 陈志英. 基于粗糙集神经网络和振动信号的高压断路器机械故障诊断[J]. 电工技术学报, 2020, 35(增刊1): 277-283.
Lin Lin, Chen Zhiying. Mechanical fault diagnosis of high voltage circuit breakers based on rough set neural networks and vibration signals[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 277-283.
[7] 万书亭, 豆龙江, 李聪, 等. 基于振动信号的高压断路器合闸特性参数在线检测方法研究[J]. 振动工程学报, 2019, 32(2): 359-367.
Wan Shuting, Dou Longjiang, Li Cong, et al. Study on on-line detection of high voltage circuit breaker closing characteristic parameters based on vibration signal[J]. Journal of Vibration Engineering, 2019, 32(2): 359-367.
[8] 孙来军. 振动信号小波包特征熵的时变与频变特性分析[J]. 高电压技术, 2007, 33(8): 146-150.
Sun Laijun. Time-variation and frequency-variation analysis of wavelet packet-characteristic entropy for vibration signals[J]. High Voltage Engineering, 2007, 33(8): 146-150.
[9] 樊浩, 李兴文, 苏海博, 等. 基于主成分分析: 支持向量机优化模型的断路器故障诊断方法研究[J]. 高压电器, 2020, 56(6): 143-151.
Fan Hao, Li Xingwen, Su Haibo, et al. Research on circuit breaker fault diagnosis method based on principal component analysis-support vector machine optimization model[J]. High Voltage Apparatus, 2020, 56(6): 143-151.
[10] 杨秋玉, 阮江军, 黄道春, 等. 基于振动信号时频图像识别的高压断路器分闸缓冲器状态评估[J]. 电工技术学报, 2019, 34(19): 4048-4057.
Yang Qiuyu, Ruan Jiangjun, Huang Daochun, et al. Opening damper condition evaluation based on vibration time-frequency images for high-voltage circuit breakers[J]. Transactions of China Electro- technical Society, 2019, 34(19): 4048-4057.
[11] 董文亮, 邹积岩, 郭兴宇. 直流真空断路器模块的机械联动特性仿真与实验研究[J]. 中国电机工程学报, 2017, 37(4): 1005-1011.
Dong Wenliang, Zou Jiyan, Guo Xingyu. Simulations and experimental research on dynamic characteristics of DC vacuum circuit breaker modules[J]. Pro- ceedings of the CSEE, 2017, 37(4): 1005-1011.
[12] Jiang Wentao, Liu Xiaoming, Chen Hai, et al. Analysis on dynamic characteristics of fast operating mechanism of vacuum circuit breaker[C]//IEEE Inter- national Conference on Applied Superconductivity and Electromagnetic Devices, Tianjin, China, 2020: 1-2.
[13] 程显, 赵海洋, 葛国伟, 等. 快速斥力机构线圈盘磁场优化设计[J]. 高电压技术, 2020, 46(8): 2643- 2653.
Cheng Xian, Zhao Haiyang, Ge Guowei, et al. Optimum design of coil disc magnetic field of rapid repulsion mechanism[J]. High Voltage Engineering, 2020, 46(8): 2643-2653.
[14] 吴振升, 王玮, 黄梅, 等. 基于相空间重构的高压断路器振动信号特征分析[J]. 现代电力, 2006, 23(1): 10-14.
Wu Zhensheng, Wang Wei, Huang Mei, et al. Analysis of characteristics of vibration signals in high-voltage circuit breakers based on phase space reconstruction[J]. Modern Electric Power, 2006, 23(1): 10-14.
[15] 阮江军, 杨秋玉, 黄道春, 等. 高压断路器机械振动信号混沌吸引子形态特性[J]. 电力自动化设备, 2020, 40(3): 187-193.
Ruan Jiangjun, Yang Qiuyu, Huang Daochun, et al. Shape characteristic analysis of chaotic attractor for mechanical vibration signal of high-voltage circuit breaker[J]. Electric Power Automation Equipment, 2020, 40(3): 187-193.
[16] 杨秋玉, 王栋, 阮江军, 等. 基于振动信号的断路器机械零部件故障程度识别[J]. 电工技术学报, 2021, 36(13): 2880-2892.
Yang Qiuyu, Wang Dong, Ruan Jiangjun, et al. Fault severity estimation method for mechanical parts in circuit breakers based on vibration analysis[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2880-2892.
[17] Takens F. Lecture notes in mathematics[M]. Berlin: Springer, 1981.
[18] 董二女. 粉末注射成形动力系统的混沌吸引子形态研究[D]. 长沙: 中南大学, 2011.
[19] 张友利. 穹窿管内油水两相流流动特性研究[D]. 天津: 天津大学, 2010.
[20] 付饶, 梁慧敏, 叶雪荣, 等. 接触器触点超程分析及其退化状态的诊断[J]. 电工技术学报, 2020, 35(1): 125-133.
Fu Rao, Liang Huimin, Ye Xuerong, et al. Analysis of the contact overtravel of contactor and its degradation state evaluation[J]. Transactions of China Electro- technical Society, 2020, 35(1): 125-133.
[21] 张婷婷, 于明, 李宾, 等. 基于Wavelet降噪和支持向量机的锂离子电池容量预测研究[J]. 电工技术学报, 2020, 35(14): 3126-3136.
Zhang Tingting, Yu Ming, Li Bin, et al. Capacity prediction of lithium-ion batteries based on Wavelet noise reduction and support vector machine[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3126-3136.
A Method of Mechanical Fault Identification of Permanent Magnet Repulsion Mechanism of Vacuum Circuit Breaker Based on Chaos Attractor
112131
(1. State Key Laboratory of Reliability and Intelligence of Electrical Equipment Hebei University of Technology Tianjin 300130 China 2. School of Mechanical Engineering Tiangong University Tianjin 300387 China 3. Chengdu Xuguang Electronics Co. Ltd Chengdu 610500 China)
In order to solve the problem that the vibration signal of repulsive mechanism of vacuum circuit breaker is transient, nonlinear, and it is difficult to quantitatively evaluate and identify the fault, this paper proposes a method of repulsive mechanism fault evaluation and identification based on chaotic attractor moment feature of attractor morphology and particle swarm optimization support vector machine. The typical faults of the repulsive mechanism in the process of opening and closing, especially the vibration signals of the opening oil buffer with different degrees of overmodulation fault, are analyzed. Firstly, the phase space reconstruction method of chaos theory and Wolf algorithm are used to obtain the maximum Lyapunov exponent, which shows that the vibration signal of repulsive mechanism has obvious chaotic characteristics. The evolution of chaotic attractor of the vibration signal is qualitatively analyzed using three-dimensional phase diagram. Then, the chaotic attractor moment theory is introduced to extract four kinds of two-dimensional attractor moments. The slope of the first region curve is calculated as the attractor morphological feature by the least square linear regression method, and the time-domain signals are extracted to form the feature vector library. Finally, the accuracy of the support vector machine algorithm and the particle swarm optimization-support vector machine combination algorithm is compared. The experimental results show that the proposed method can accurately identify the fault types of repulsive mechanism.
Vacuum circuit breaker, repulsion mechanism, oil buffer, attractor morphology, support vector machine
10.19595/j.cnki.1000-6753.tces.210970
TM561
中央引导地方科技发展专项(20ZYJDJC00060)和河北省自然科学基金面上项目(E2021202186)资助。
2021-07-02
2021-07-29
刘晓明 女,1968年生,教授,博士生导师,研究方向为现代电器设计与应用、高电压与绝缘技术、智能电器。E-mail: liuxiaoming@hebut.edu.cn(通信作者)
张煦松 男,1996年生,硕士研究生,研究方向为现代电器设计与应用、电器设备状态检测、智能电器、混沌分析。E-mail: 1508189330@qq.com
(编辑 崔文静)

