基于受激布里渊散射的高精度多微波频率测量
张先玉, 梁 涛, 安 康
(国防科技大学第六十三研究所, 江苏 南京 210007)
0 引 言
微波信号参数测量技术在雷达、无线通信、空间探测等领域具有极其重要的作用,微波信号的参数繁多,包括幅度、相位、频率、调制方式、极化方式等,每种参数均能反应具体的性能指标并包含诸多有用信息。其中,频率信息是微波信号最为重要的参数之一,广泛应用于雷达预警、电子战、电磁感知等领域中。然而,受电子器件的瓶颈限制,传统的电域微波频率测量技术一般受限于18 GHz的测量范围。另一方面,微波光子学技术具有带宽大、损耗低、重量轻、不受电磁干扰影响等诸多优点,因此利用光子学技术进行微波频率测量具有极大的技术优势和应用前景,被视为未来电子战、雷达、电磁频谱感知等领域的重要发展方向,得到了大量的关注和研究。
早期的微波光子频率测量技术主要是利用频率-幅度映射进行频率估计,通过一定的光信号处理,将频率信息映射为光信号或者微波信号的功率,利用映射关系估计出微波信号的频率信息,此类方法测量范围大,具有一定的测量精度,但是仅能测量单个微波信息,适用范围不广。为实现多频率微波信号的测量,业界提出并研究了多种频率-时间映射方案,利用色散介质或者光纤布拉格光栅产生的不同时延差进行不同频率的测定,但是该类方案分辨率不高且测频误差较大。为实现高分辨率高精度多频率测量,文献[23]提出了一种基于受激布里渊散射的微波频率测量方案,利用受激布里渊散射效应将相位调制转变为强度调制,通过测量微波信号的功率实现微波频率测量,该方案的测量误差小于30 MHz。为进一步提高频率测量的范围,文献[24]利用两个间距为2倍布里渊频移的泵浦光信号将测量范围扩大至4倍布里渊频移范围,该方案的分辨率为39.93 MHz,测量误差为1.6 MHz。文献[25]基于受激布里渊散射针对不同频段建立了频率-功率映射和幅度比较函数(amplitude comparison function, ACF),将测频范围扩大至38 GHz,但该方案系统复杂,实现成本较高。文献[26]利用可调激光器产生泵浦光,利用受激布里渊散射效应打破相位调制的边带平行从而实现频率测定,该方案中可调激光器的控制精度制约了测频精度。进一步地,文献[27]同时利用了双阶段受激布里渊散射和非线性拟合提高了测频方案的分辨率和精度,最小分辨率达到18 MHz,测量误差小于5 MHz,但该方案采用强度调制,载波及边带功率大,输出光功率的增益较小。
为实现高精度多微波信号瞬时频率测量,提出了一种基于受激布里渊散射的微波频率测量方案。利用双平行马赫曾德尔调制器(dual parallel Mach-Zehnder modulators, DPMZM)对待测微波信号和扫频信号进行抑制载波单边带调制(carrier suppressed single sideband modulated, CS-SSB),利用两阶段受激布里渊散射结构减小布里渊增益的线宽,为避免使用高速光电探测器,方案通过光功率测量实现频率估计。为进一步提升扫描速度和测量精度,建立了两阶段频率测量,首先利用较大的扫频间隔实现频率粗估计,之后通过建立幅度比较函数进行频率精估计。另外,本方案通过调整DPMZM的参数,可利用低扫描频率实现高频段频率测量。
1 测频方案
所提的基于受激布里渊散射的微波频率测量方案系统模型如图1所示。

图1 所提多微波频率测量方案系统框图Fig.1 Schematic of proposed multiple microwave frequency measurement scheme
一个可调激光器(laser diode, LD)生成一路光载波信号,之后通过3 dB光耦合器(optical coupler, OC)分成上下两路光信号。两路光信号分别通过两个偏振控制器(polarization controller, PC),之后分别输入两个DPMZM调制器中。上下两个DPMZM调制器分别调制扫描信号和未知微波信号。通过调整参数使两个DPMZM分别生成两路CS-SSB信号,上路信号可根据需要设置为上边带或者下边带CS-SSB信号,下路信号为下边带CS-SSB信号。为补偿传输损耗并控制光功率,将调制后的上路泵浦光信号通过掺饵光纤放大器(Er-doped fiber amplifier, EDFA)进行功率放大。下路信号通过双阶段受激布里渊散射效应结构,单个阶段由光隔离器(isolator, ISO)、色散位移光纤(dispersion shift fiber, DSF)、光环形器(circulator)组成。上路信号通过3 dB光耦合器分为两路信号,分别作为两阶段受激布里渊散射的泵浦光。最后,利用光功率计测量并记录输出的光信号功率值,之后通过一定的信号处理得到未知微波信号的频率估计值。
2 信号调制及频率粗测量
首先考虑利用DPMZM进行光信号调制,DPMZM的内部结构如图2所示,该调制器由两个子调制器MZM1、MZM2和主调制器MZM3组成。其中,MZM1和MZM2具有单独的射频信号(radio frequency, RF)输入端口,各端口输入信号的相移分别为,,和,3个调制器均有单独的直流电压控制端口,和。
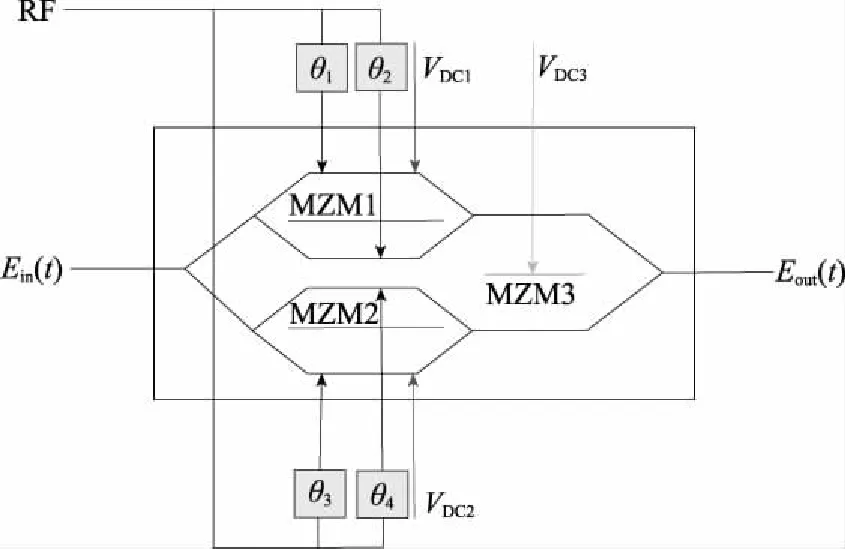
图2 DPMZM内部结构图Fig.2 Inernal strucure diagram of the DPMZM
由图2结构可知,DPMZM的输出光信号可表示为

(1)
式中:和分别表示光载波的幅度和角频率;和表示调制信号的幅度和角频率;=(π)为调制深度。
将MZM1和MZM2调制在最小传输点,即:π=π,π=π,=+π,=+π。不失一般性,可设定=π。另外,设定=+π2,=π。
将MZM调制器均设置在小信号调制模式,即≪1时,高阶贝塞尔函数近似为零,此时可得

(2)
由此可知,当=2时,输出信号为下边带CS-SSB调制信号,即:

(3)
而当=-2时,输出信号为上边带CS-SSB调制信号,即:
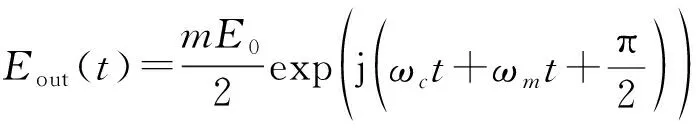
(4)
图3为受激布里渊散射过程示意图及相关的频率关系图,其中为光载波频率值,为布里渊频移,和表示两个未知微波信号的频率。典型地,可考虑0≤≤,≤≤2。图3(a) 为经过扫描信号调制的泵浦光信号,通过调整光边带可实现不同频段信号的频率测量。进一步地,通过调整泵浦光信号的功率值,使其超过光纤的受激布里渊散射门限值,即可发生受激布里渊散射效应。图3(b) 为未知待测信号调制的光边带信号,若未知信号的频率落在泵浦信号的布里渊增益谱内,该光信号的功率即可得到放大。图3(c) 为受激布里渊示意图,当泵浦信号和待测信号的频率满足一定关系时,即发生受激布里渊散射效应,待测信号的功率得到有效放大,通过测定输出信号的光功率,即可判断并计算得到未知信号的频率值。
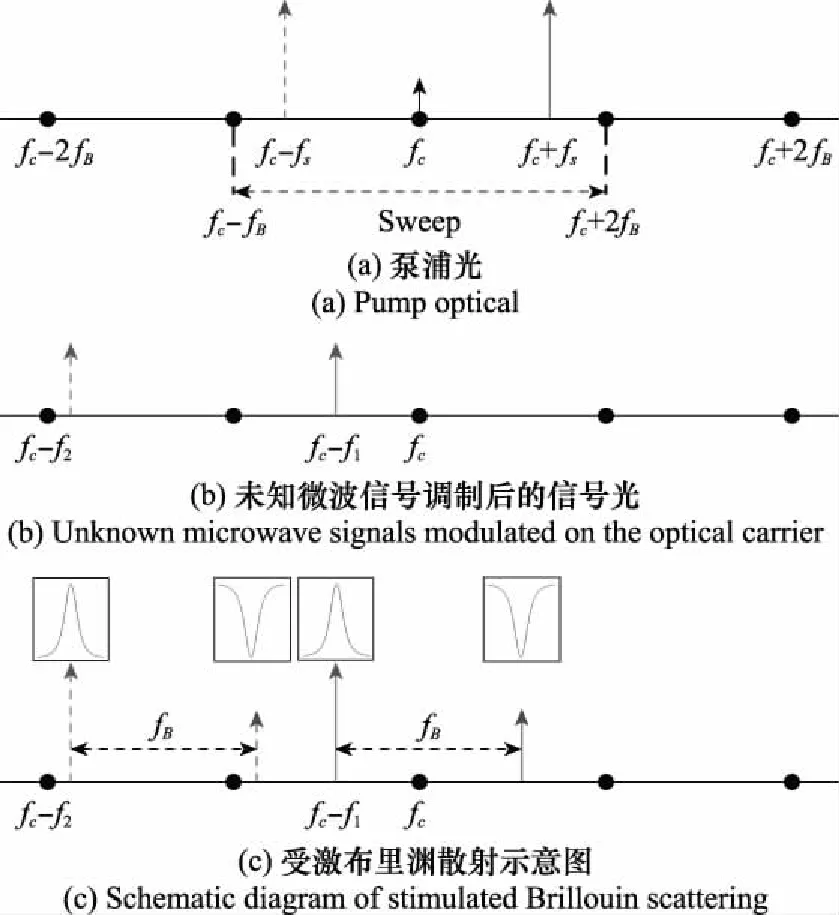
图3 所提多微波频率测量方案原理示意图Fig.3 Principle of the proposed multiple microwave frequency measurement scheme
光纤的受激布里渊散射增益可表示为

(5)
式中:为受激布里渊散射增益峰值;Δ为受激布里渊散射线宽;表示相对于受激布里渊散射峰值的频偏。
由式(5)可知,单阶段受激布里渊散射结构增益的半最大带宽为

(6)
而双阶段受激布里渊散射效应结构的半最大带宽为

(7)
图4为单阶段和双阶段增益谱的比较,可见,相比单阶段布里渊结构,双阶段布里渊结构的线宽减小,这对于提高测频系统的分辨率和测量精度极为有利。

图4 单阶段和双阶段受激布里渊散射增益谱对比图Fig.4 Comparison of stimulated Brillouin scattering gain for one and two stages


(8)
若泵浦光为下边带CS-SSB调制时,则待测微波信号的频率为

(9)
所提方案容易实现[0,2]的频率测量,实际上,该方案通过调整扫描信号的范围,很容易实现宽频域的频率测量,由于本方案中未使用高速光电探测器,该方案的测频范围主要受限于调制器的响应带宽。
另外,该方案依靠扫描信号可实现对多个频率的测定,因此只有当信号的变化速率小于扫描周期,该方案才能有效截获并测量所有的未知信号,扫描周期是影响方案有效性的重要参数。为提升扫描速率,需要适当扩大扫频间隔。为避免信号遗漏,本方案选定Δ2作为扫频间隔,这样即可保证总有一个扫描频率落在[-(Δ)4,+(Δ)4]区间内,实现频率的粗测量。因此,该方案粗测量的测量误差为±Δ4。根据文献[30]可知,光纤的受激布里渊散射线宽在88 MHz左右,即频率粗测量的误差为±22 MHz。
3 频率精测量
由前面介绍的频率粗测量方案可知,受扫频间隔的影响,频率粗测量的精度不高。为提高测量精度,可采用两种方案:第一种方案是进一步减小扫频间隔,提高测量精度,但此种方案会导致扫描周期变长,使得方案会遗漏部分变化迅速的微波信号,这对于雷达、电子战等应用领域往往是难以接受的;另一种方案是通过适当的算法补偿,减小频率测量的误差。本文选择通过误差补偿的方式进行频率精测量。
由式(5)可知,受激布里渊散射增益谱在峰值左右具有单调性,可利用这一特性建立误差补偿映射关系,对粗估计值进行误差补偿。

进一步地,利用输出光功率的比值,可建立ACF为

(10)
进一步地,可知ACF的测量值为

(11)
通过比较即可得到频率差值的估计值Δ,可得修正的频率测量值为
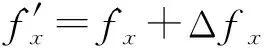
(12)
4 仿 真
为验证所提方案的有效性,本节利用VPI和Matlab进行实验仿真验证。首先利用VPI搭建仿真系统,如图5所示。激光器的中心频率为193.1 THz,功率为10 dBm,上下支路均利用DPMZM实现CS-SSB调制,为补偿光功率的损耗,上支路通过一个EDFA,增益为20 dB,之后分为两路作为两段受激布里渊散射效应段的输入泵浦光功率。下支路信号通过两段受激布里渊散射结构段,各段均有光隔离器、DSF光纤及光环形器构成,光纤长度设定为5 km,受激布里渊散射频移设定为10 GHz,受激布里渊散射线宽设定为100 MHz。最后,改变上支路扫描信号的频率为0~10 GHz,扫描频率步长设定为50 MHz,测量并记录系统输出的光功率,通过计算得到微波信号的功率值。
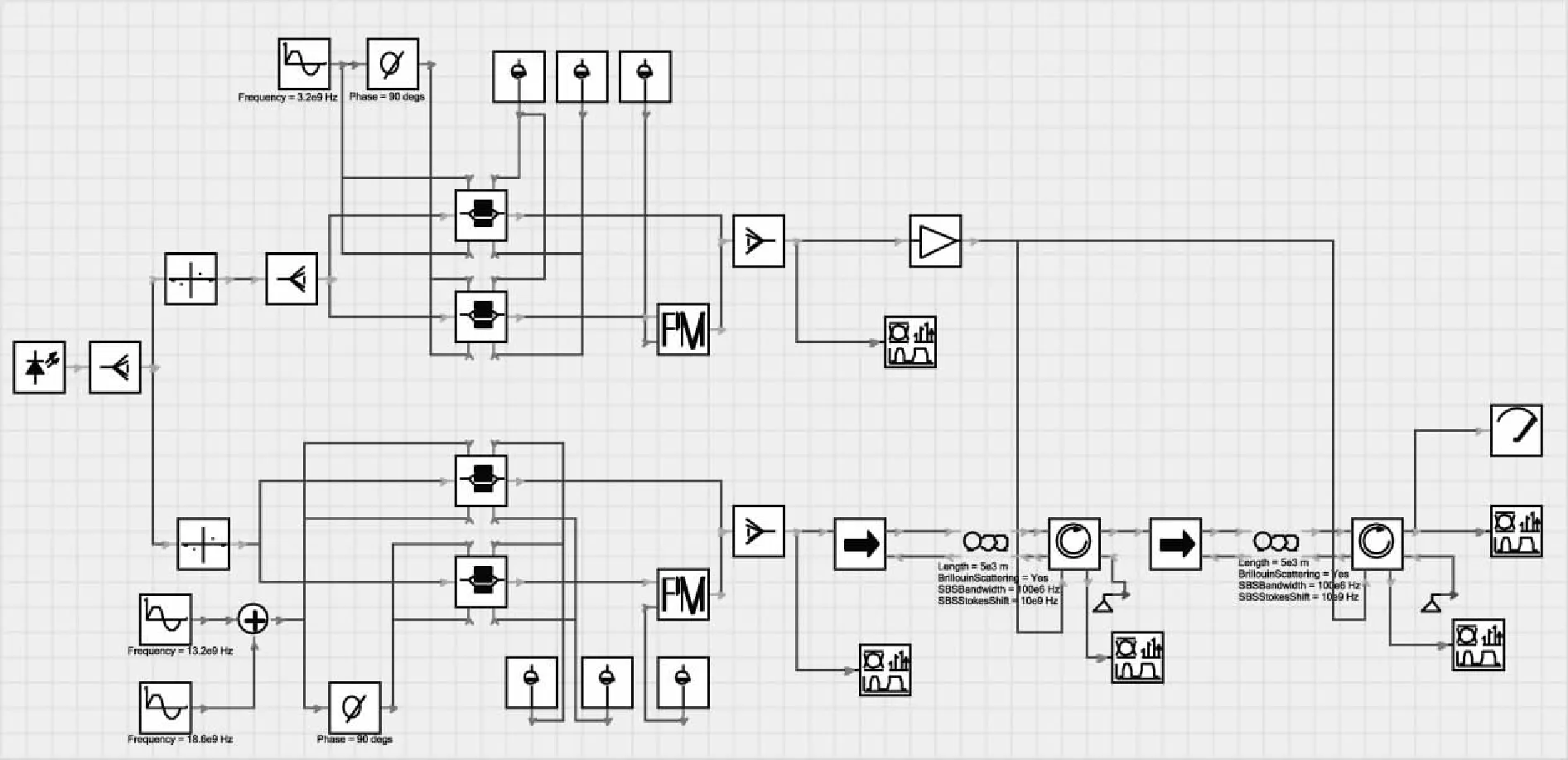
图5 所提多微波频率测量方案VPI仿真结构图Fig.5 VPI simulation structure diagram of the proposed multiple microwave frequency measurement scheme
上路DPMZM输出的信号光谱图如图6所示,明显可见,信号载波得到了有效抑制,一阶单边带信号比高阶边带功率高出35 dB,可见输出的CS-SSB信号质量非常优良。因此,该结构可有效避免载波及其他边带引起的布里渊增益,得到虚假的估计值。同时,该结构可得到较大的增益系数,输出光功率的变化幅度较大,便于进行比较计算。
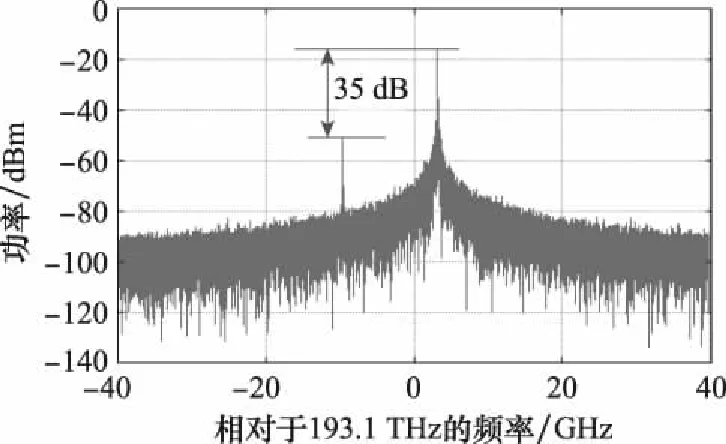
图6 CS-SSB调制信号光谱图Fig.6 Optical spectrum of the CS-SSB signal
不失一般性,假设[0,10 GHz]有两个未知信号,频率分别为5.7 GHz和7.8 GHz。假设[10 GHz,20 GHz]有两个未知信号,频率为13.2 GHz和18.6 GHz。通过设置偏置电压,实现泵浦信号上边带或者下边带CS-SSB调制,扫描信号范围设定为[0,10 GHz],则对应的输出光功率的测量值如图7和图8所示,从图7和图8可见,所提方案能准确捕获相应的未知信号,所提结构能产生较大的光功率谱增益,利用式(8)和式(9)通过简单计算即可得到频率的粗估计值。
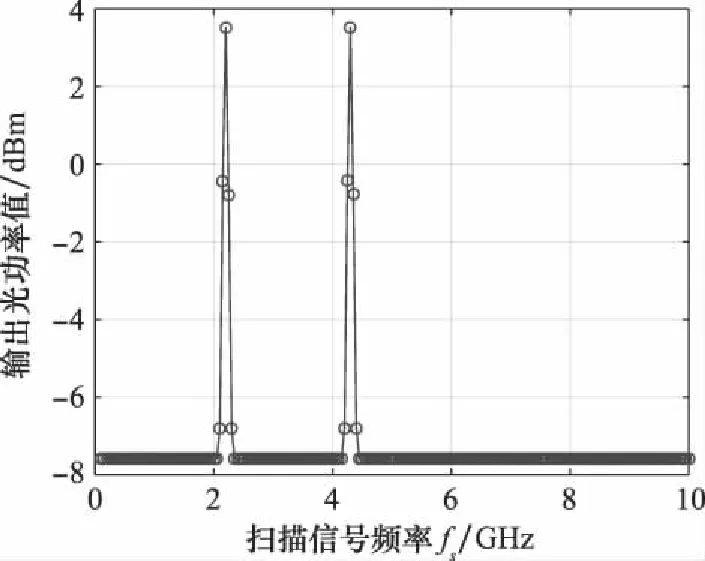
图7 扫描信号为上边带CS-SSB调制时的输出光功率扫描曲线Fig.7 Power values of the output optical signal when the scanning signal is modulated by upper sideband CS-SSB

图8 扫描信号为下边带CS-SSB调制时的输出光功率扫描曲线Fig.8 Power values of the output optical signal when the scanning signal is modulated by lower sideband CS-SSB
为进一步提高方案的测频精度,可利用现有的测量值进行频率测量误差补偿。图9为ACF的理论值与测量值的对比图,可见测量值与理论值的吻合度较高。图10为相应的平均频率误差估计值,经过频率误差补偿后,测频误差可限制在±3 MHz内。进一步地,调整未知信号的频率值,对[0,20 GHz]频段的未知信号进行测频,扫描信号范围为[0,10 GHz],通过频率测量及误差补偿,最终测量结果如图11所示。可见,该测量方案能利用低频段的扫频信号实现高频段信号的频率测量,且经过误差补偿后,所提方案的测频精度较高,能够实现大范围高精度的微波信号频率测量。
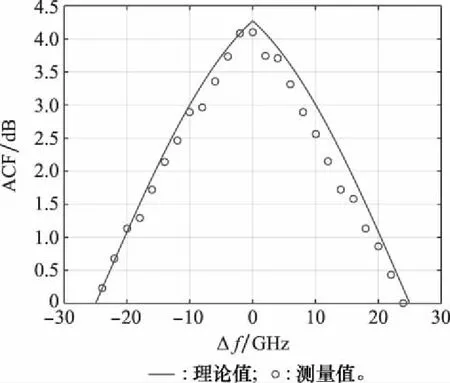
图9 ACF理论值及实验值对比图Fig.9 Comparison of the theoretical and experimental values of ACF

图10 频率测量误差示意图Fig.10 Frequency measurement error diagram

图11 频率测量结果与误差示意图Fig.11 Frequency measurement results and error diagram
5 结 论
本文提出了一种基于受激布里渊散射的高精度多微波频率测量方案,利用DPMZM分别实现待测信号和扫描信号的CS-SSB调制,利用双阶段受激布里渊散射结构减小布里渊线宽。为避免使用高速光电探测器,所提方案通过测量输出光功率值实现信号频率的粗测量。另外,通过调整DPMZM的参数实现泵浦信号的上边带或者下边带CS-SSB调制,利用低频段的扫描信号实现高频段的微波信号频率测量,降低了方案的实现难度。为进一步提高测频精度,通过建立ACF函数对频率估计值进行误差补偿,进一步降低了算法的测量误差,方案测频误差为±3 MHz。

