基于改进遗传算法的多直角贴装机器人路径协同规划

陈 宝，田 斌，周占伟，陈 静，陈雪婷，李经民

(1.大连理工大学 辽宁省微纳米技术及系统重点实验室，辽宁 大连 116024；2.北京卫星制造厂有限公司，北京 100048)

0 引言

复合结构板的尺寸较大，若采用传统单机器人带多贴片头的方式进行贴片，将产生过多往复取片的空行程，大大降低机器人贴片效率[1，2]；若采用多直角贴装机器人协同贴片虽能满足需求，但需采用遗传算法进行协同路径规划。

采用传统遗传算法进行协同路径规划存在易陷入局部最优解和早熟的问题，目前虽然一些学者针对遗传算法存在的问题进行了改进与优化，如引入局部算子[3]、最小准则[4]、灾变算子[5]、自适应交叉和变异算子[6]等，但是针对多直角贴装机器人共用X轴且贴装环境复杂的情况，以上算子在编码、避免碰撞、收敛速度等方面仍有提高空间。

本文充分考虑多机器人碰撞的问题，建立多直角贴装机器人协同贴片的数学模型，引入碰撞惩罚、分组进化、部分匹配交叉、自适应变异算子对遗传算法进行改进，并采用MATLAB对3个直角机器人协同路径规划问题进行仿真实验。

1 多直角贴装机器人协同贴片数学模型建立

图1为3个直角贴装机器人在复合结构板上的分布情况，并以此建立数学模型。

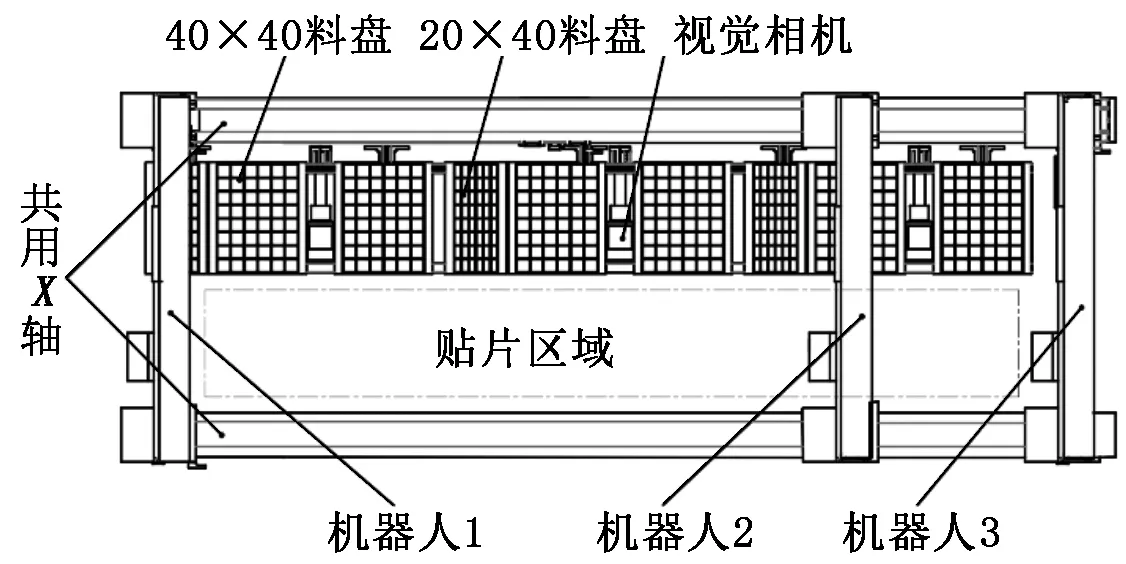
图1 3个直角贴装机器人在复合结构板上的分布

将直角贴装机器人看做是多旅行商问题中的旅行商，复合结构板上的贴片点看做是城市集合。定义如下：总共有3个直角贴装机器人，N个待贴片点，每个贴片点有被贴片且只被贴一次。由于贴装效率的高低取决于所有直角贴装机器人走的路径总长度，因而本文的优化目标是使得机器人走的路径总长度D最短，建立的数学模型为：

.

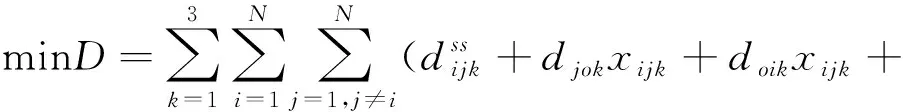
(1)

约束条件为：

xijk∈{0,1}.

(2)

(3)

(4)

(5)

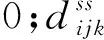
式(3)确保每一个需贴片点都被贴上料片；式(4)和式(5)确保每个贴片点只被贴一次。

2 改进的遗传算法

2.1 编码与生成初始种群

由于复合结构板上的贴装区域类似于栅格地图，因而可以将贴装区域用栅格地图表示，如图2所示。

图2中,白色区域表示贴片区域，黑色区域表示障碍物，每1格代表贴1片40 mm×40 mm料片，半格为贴1片40 mm×20 mm料片，并将贴片点按顺序以数字集E=1,2,3,…，N编号。将贴片点编号随机分配给3个机器人，以此生成一条染色体。重复此过程，生成种群池所需数量的染色体，以这些染色体组成初始种群，存储到三维矩阵中，如图3所示。

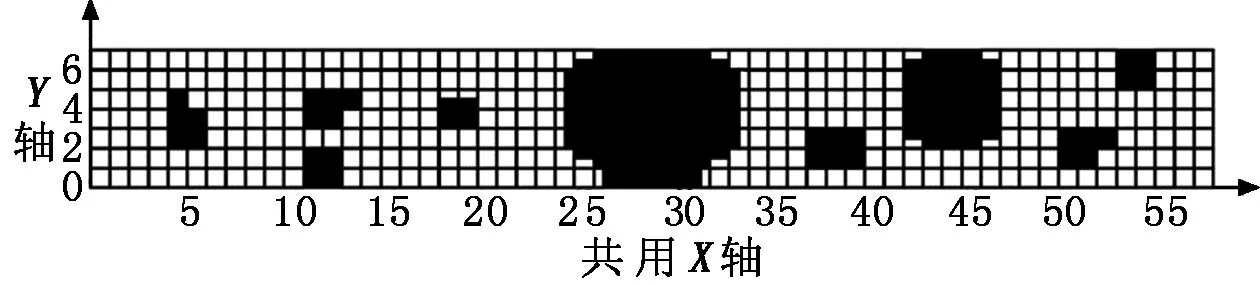
图2 栅格地图

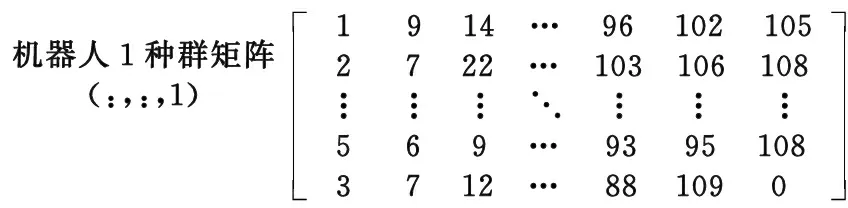
图3 初始种群三维矩阵

2.2 基于时间序列的碰撞惩罚适应度函数

本文是选用3个机器人进行协同贴片，采用遗传算法优化路径，并且路径不可产生碰撞，否则将造成设备的损坏。因而选取直角贴装机器人总路径长度D的倒数作为适应度函数的一个分量f1：

(6)

可通过加速度函数反计算得到某个直角坐标机器人在任意时刻的位置集合Pk={Pk1,Pk2,…Pkn}，重复此过程，可得到各机器人的时间序列总集合{P1,P2,P3}。如果3个机器人的时间序列交集M为空集，则碰撞惩罚系数ui为1，否则为0，将其作为适应度函数的另一个分量：

M=P1∩P2∩P3.

(7)

(8)

综合式(6)和式(8)，本文遗传算法所构造的适应度函数为：

minf=ui·f1.

(9)

2.3 基于分组进化的选择算子

本文在传统遗传算法基础上引入分组的思想，将总种群分为精英组、优质解组以及劣质解组进行分组进化。首先对初始种群按照适应度值进行排序，选出适应度值最靠前的几个解放入精英组，不参与后续遗传操作直接放入下一代新种群；选出适应度值排名前半部分(除去精英组成员)的解放入优质解组，后续采用单点交叉和单点变异；剩余的解则放入劣质解组，后续采用单点交叉和多点变异。

2.4 部分匹配交叉算子

结构板上每个贴片点必须保证有且只有一次访问，因而需采用部分匹配交叉算子来保证这一约束条件。部分匹配交叉算子类似于单点交叉算子，随机生成一个交叉点，将交叉点之后的交叉区域进行交换。此时，生成的两条染色体一般存在重复和缺失的基因，为了修复染色体需要在交叉区域内建立基因的映射关系，根据此关系消除重复基因和增加缺失基因，操作过程如图4所示。

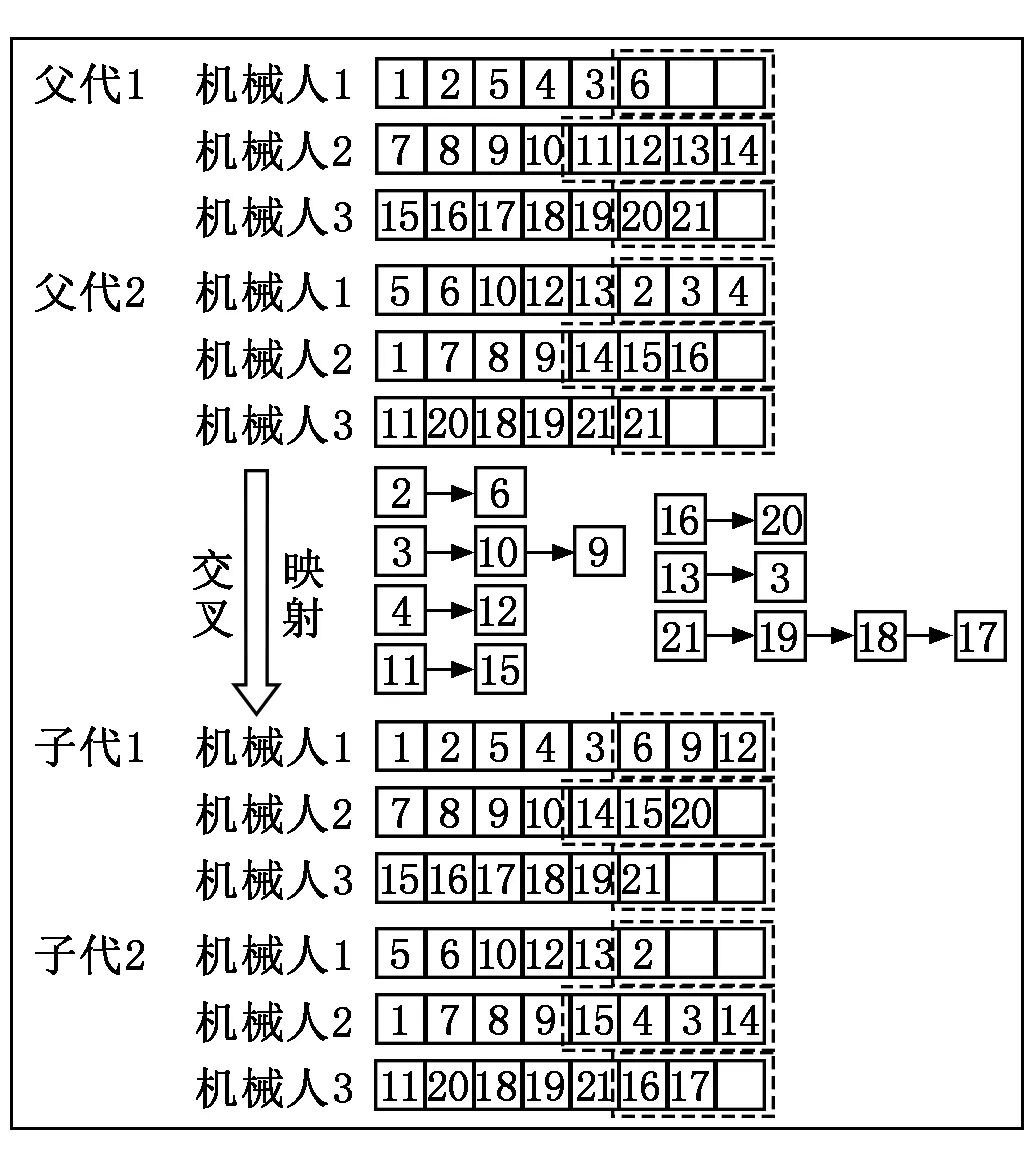
图4 部分匹配交叉算子操作过程

2.5 自适应变异算子

遗传算法前期主要通过交叉算子产生新的优良染色体，需要采用低的变异概率来保持，从而实现优良个体的快速积累；到算法后期由于种群全是类似的染色体，如若还是采用静态变异概率，则算法易陷入局部最优解。因而，本文采用一种自适应变异算子，随着当前进化代数g从1增大到最大进化代数gmax，变量t逐步从0增大到1，与此同时变异概率Gm也逐步增大到初始变异概率Gm0的2倍，从而产生更多新个体，提高种群丰富度，避免陷入局部最优解，即：

(10)

Gm=Gm0·2t.

(11)

3 仿真实验与结果分析

3.1 实验准备与参数设计

根据本文的算法，采用MATLAB程序对3个直角贴装机器人进行协同路径规划仿真实验。机械硬件采用直线电机组成的直角坐标机器人，速度为2 m/s，加速度为12 m/s2；每个机器人Z轴末端都带有两个真空吸盘，复合结构板如图2所示。

电脑开发环境为Win11和MATLAB2020a。仿真设定的种群规模为500，最大迭代次数为600；精英解组选择概率为0.01；优质解组的交叉概率为0.8，初始变异概率为0.1；劣质解组交叉概率为0.9，初始变异概率为0.2。

3.2 实验结果与分析

采用传统遗传算法和本文改进遗传算法得到的路径优化曲线如图5所示。

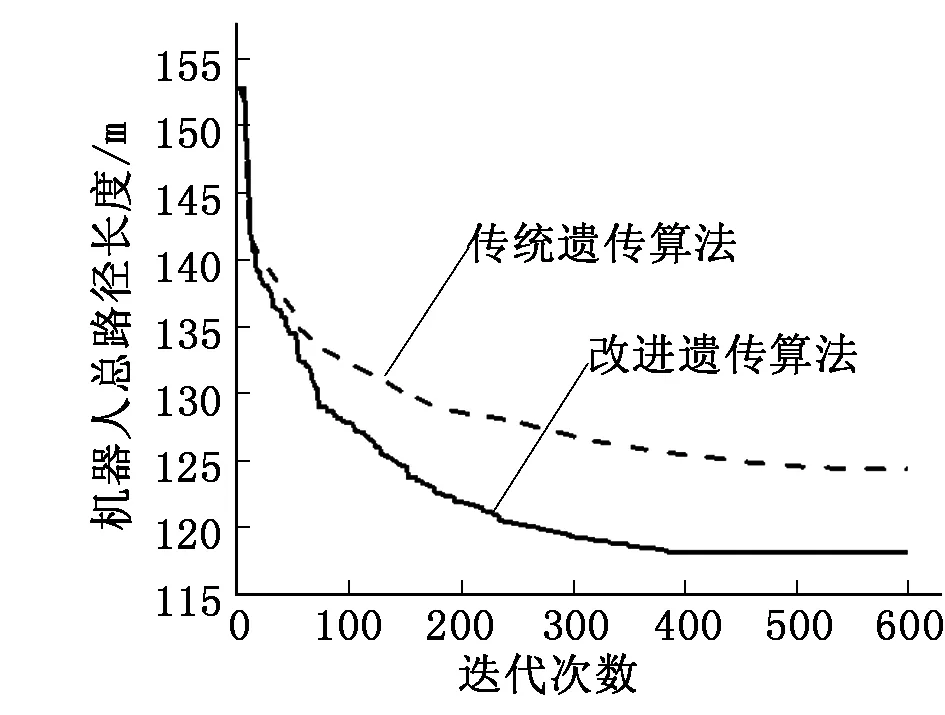
图5 遗传算法优化曲线

由图5可知，采用本文的改进遗传算法在389代得到长118 196 mm的最优路径，而采用传统遗传算法在526代得到局部最优解，路径长度为124 383 mm。本文遗传算法较传统平均分配贴片区域的路径长度152 771 mm优化了22.6%，较传统遗传算法路径长度优化了4.9%，收敛速度加快26.1%。

图6为3个机器人最优路径的时间序列曲线,可以看出，任意时刻的3条曲线都没有交点，表明3个机器人在协同贴装结构板的过程中不会发生碰撞。

图6 3个机器人最优路径的时间序列曲线

4 结论与展望

本文针对多直角贴片机器人协同路径规划的问题，提出了适合本问题的带有碰撞惩罚、分组进化、部分匹配交叉和自适应变异的改进遗传算法。经3个直角贴装机器人仿真实验得到，本算法相对平均分配贴片区域，降低了路径长度；相对传统遗传算法，加快收敛速度，不易陷入局部最优解。接下来将着重于研究加入其他交叉算子和变异算子，以进一步提高算法的收敛速度和稳定性；或者研究本算法在其他种类贴片机器人协同路径规划中的应用。