焊缝的随机振动多轴频域疲劳方法研究

苏楷通，温朋哲，黄 伟

(1.西南交通大学 机械工程学院，四川 成都 610031；2.天津市政工程设计研究总院有限公司 轨道交通设计研究院，天津 300392)

0 引言

大多数焊接结构在工作中均会承受随机载荷，其应力状态多为多轴应力状态，工作中多个应力分量独立地随时间变化，难以估算疲劳损伤[1]。焊接接头的应力集中效应使其疲劳强度低于母材疲劳强度，在随机载荷下，焊接接头通常会产生疲劳裂纹，引起结构疲劳破坏。因此研究焊接接头的随机振动多轴疲劳强度，对保证焊接结构的安全性具有现实意义。

根据描述方式，随机振动分析方法分为时域法和频域法，后者由于思路简单、计算量小，在工程上得到广泛应用。在多轴应力状态的频域法中，临界面法(CPM)[2]计算的疲劳寿命与实验较吻合。结构应力法[3]对网格不敏感，其主S-N(S为应力水平，N为寿命)曲线适用于不同的板厚、焊接接头形式及加载方式的组合，该方法能有效提高焊接结构疲劳损伤预测的准确性，被应用于随机振动频域内，形成了频域结构应力法(FSSM)[4]。FSSM是结构应力法的推广，因此具备结构应力法的优点。本文以铁道车辆转向架悬挂设备天线梁为分析对象，应用CPM与FSSM预测了天线梁焊缝的随机振动疲劳损伤，对比分析了两种方法计算的损伤值差异。

1 随机振动疲劳理论

定义结构应力范围Sr的功率谱密度为S(f)(f为频率，f>0)，宽带随机过程在频域下的累计损伤值D为：

(1)

其中：nl、Nl分别为应力水平σl对应的循环数与寿命，l为应力水平的编号；vp为应力峰值的期望速率；T为时间间隔；C、k为材料常数；P(Sr)为应力范围Sr的概率密度函数。

当D达到1时，结构发生疲劳破坏，疲劳寿命TD为：

(2)

(3)

D3=1-D1-D2

，

2 焊缝随机振动频域分析方法

2.1 CPM

临界面是指在随机激励下发生疲劳断裂的平面，临界面的法向向量n垂直于临界面，n的位置描述见图1。平面Δ为n所在的平面，定义n及系数向量d为：

(4)

(5)

其中：θ为n与整体坐标系z轴的夹角；Φ为n在xy平面的投影与x轴的夹角；lη、mη、nη分别为n与x轴、y轴、z轴的方向余弦。

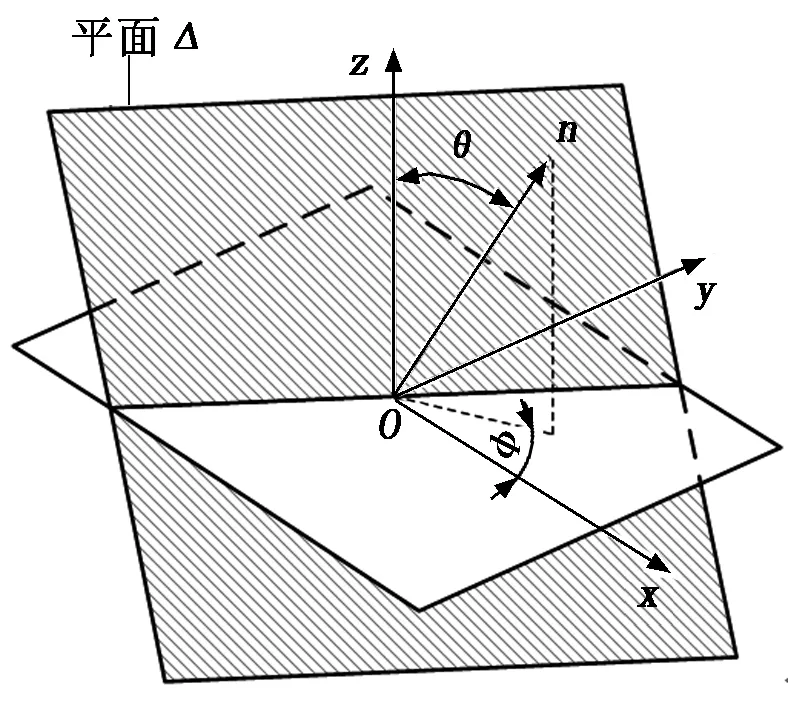
图1 法向向量n的位置描述

假设结构只有一个输入激励，输入激励的PSD(Power Spectral Density, 功率谱密度)为GL(f)，对于节点P0，激励作用下的应力传递函数为QC(f)：

诊断的行为主体(主要是医生)如果缺乏足够的临床知识，就很容易发生误诊漏诊。例如1例发热、颈部淋巴结肿大的年轻患者，合并脓性胸水。尽管胸水中细菌培养为阴性，仍诊断为细菌性化脓性胸膜炎。给予胸腔置管引流脓液，联合抗生素治疗无效。更换管床医生改变了诊断思路，指出结核性胸膜炎的胸水一般呈现黄色清亮透明，但也可以表现为脓性,称为结核性脓胸，此时脓液中很容易找到结核杆菌。结果果然在胸水里面发现抗酸杆菌阳性，纠正了最初的诊断，改用抗结核治疗方案。

QC(f)=[σx(f)σy(f)σz(f)τxy(f)τxz(f)τyz(f)].

(6)

其中：σx(f)、σy(f)、σz(f)为整体坐标系下x轴、y轴、z轴的正应力响应值；τxy(f)、τxz(f)、τyz(f)为整体坐标系下xy平面、xz平面、yz平面的剪应力响应值。

结合式(6)得到6×6的节点应力张量的PSD矩阵Gσ(f)：

(7)

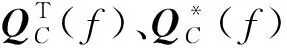
结合系数向量d计算节点P0的等效应力功率谱密度函数Ge,p(f)：

Ge,p(f)=dTGσ(f)d.

(8)

使用方差法确定临界面的具体位置。方差法认为等效应力的方差达到最大值时对应的平面就是临界面。定义等效应力张量的协方差矩阵μ：

(9)

协方差矩阵μ的分量μij(i,j=1,…,6)计算公式为：

(10)

等效应力方差μeqv的计算式为：

μeqv=dTμd.

(11)

使用方差法确定节点P0的临界面后，计算临界面上的Ge,p(f)以及谱参数,依据式(2)和式(3)预测P0的疲劳寿命。

2.2 FSSM

假设板厚为t的焊缝截面上具有弯曲应力σb和膜应力σm，结构应力σs与外力平衡[6](如图2所示)，等于σm与σb之和，即：

(12)

其中：fx、my分别为焊线在单位长度上的力和力矩，简称线力和线矩，焊线定义在焊趾上。

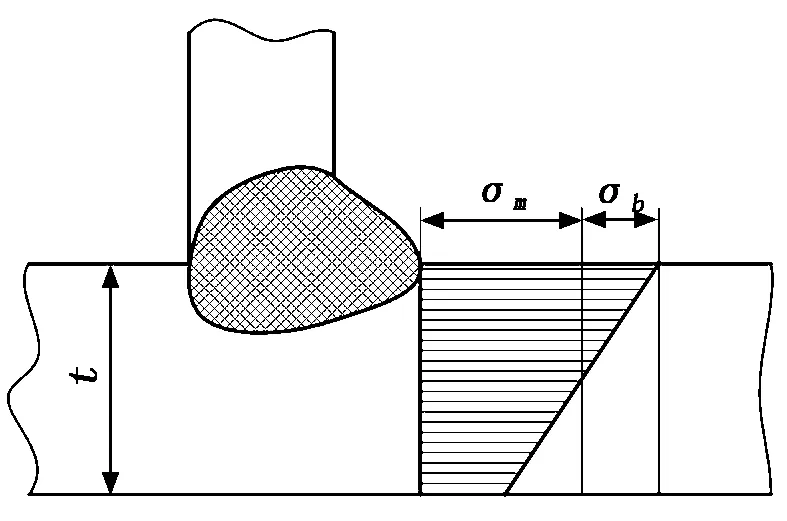
图2 与外力平衡的结构应力

对于n个节点的非封闭焊线，节点编号为1，2，…，n-1，n，焊线上的节点距离分别为l1，l2，…，ln-1，其线力矩阵fx、线力矩矩阵my与节点力矩阵Fx和节点力矩矩阵My有关[6]，即：

(13)

其中：L为单元长度等效矩阵。

结合式(12)与式(13)计算结构应力矩阵σs：

(14)

在频域内，结合式(14)计算结构应力的传递函数矩阵Hσ(f)：

(15)

其中：Fx(f)、My(f)为节点力及节点力矩的传递函数矩阵。

定义焊线上第p(1≤p≤n)个节点的结构应力传递函数为Hσ,p(f)，等效结构应力传递函数Hes,p(f)的表达式为：

(16)

其中：m为裂纹扩展指数，m=3.6；rp(f)为第p个节点的载荷弯曲比的传递函数，rp(f)=Δσb,p(f)/(Δσm,p(f)+Δσb,p(f))，Δσm,p(f)与Δσb,p(f)分别为焊线第p个节点的膜应力范围与弯曲应力范围的传递函数；I(rp(f))为rp(f)的无量纲函数。

假设结构只有一个输入激励，输入激励的PSD为GL(f)，第p个节点的等效结构应力响应功率谱Ges,p(f)的计算式为：

(17)

确定Ges,p(f)后，结合Dirlik模型、主S-N曲线与线性累计损伤准则计算第p个节点的随机振动疲劳寿命。FSSM的主S-N曲线及其参数见图3。

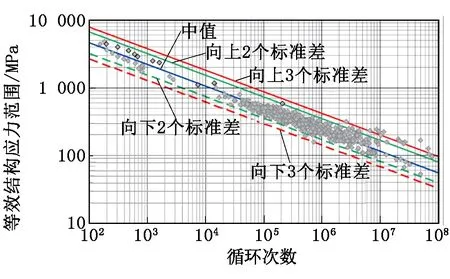
图3 FSSM的主S-N曲线及其参数

3 焊缝随机振动频域方法的应用

3.1 有限元模型

本文主要采用八节点六面体的实体单元建立铁道车辆转向架悬挂设备天线梁模型，为模拟天线梁较真实的承载情况，建立了部分侧梁模型，天线安装座下方150 mm处固定有10 kg的天线质量点，天线梁有限元模型如图4所示。

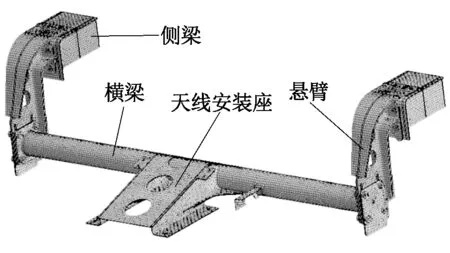
图4 天线梁有限元模型

3.2 加速度PSD的选取

基于IEC 61373-2010标准，在垂向、横向和纵向上对天线梁施加5 h的加速度激励，激励的定义见图5。图5中，a为加速度功率谱密度函数。其中三向激励的标称值X分别为6.12(m/s2)2/Hz、4.62(m/s2)2/Hz与1.32(m/s2)2/Hz。分别计算三向激励的疲劳损伤并进行累加，总损伤值D0由公式(18)计算得到，当D0达到1时，结构发生疲劳破坏。

(18)

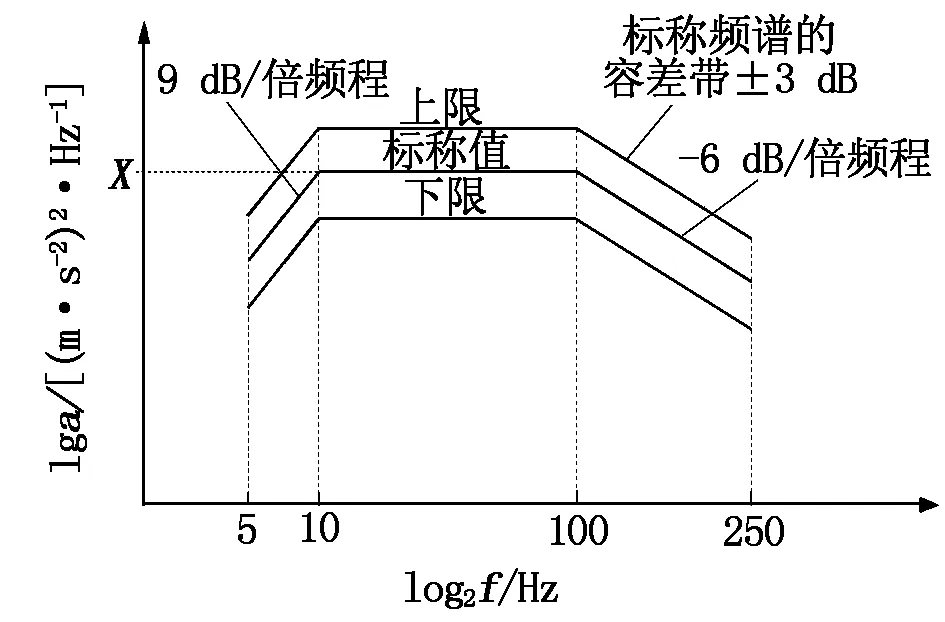
图5 加速度PSD函数

其中：Nv、Nh、Na分别为垂向、横向和纵向激励下的寿命值，s。

3.3 计算结果

选取BS 7608标准规定的F级S-N曲线，应用CPM与FSSM预测了天线梁焊缝的随机振动疲劳损伤值。两种方法计算得到的疲劳薄弱节点(前10个最大损伤值的节点)损伤值分别如表1、表2所示。

从表1与表2中看出，CPM计算的损伤值范围为0.51～0.90，FSSM计算的损伤范围为0.28～0.88，前者损伤值结果较后者大。

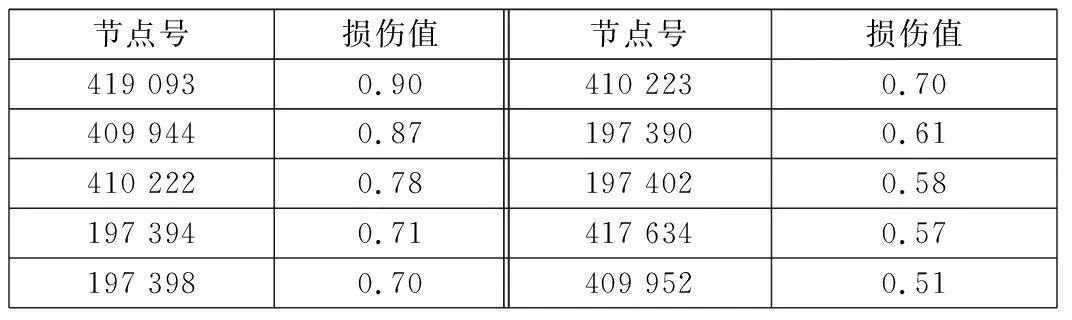
表1 CPM计算的损伤值

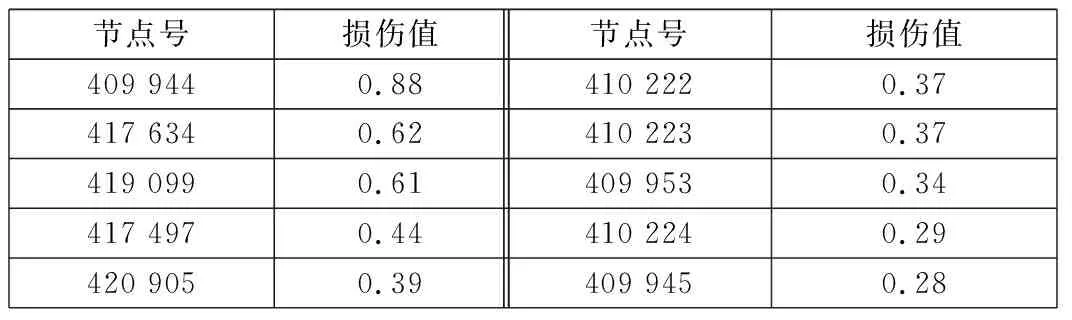
表2 FSSM计算的损伤值

4 结论

依据IEC 61373与BS 7608标准，应用CPM与FSSM预测了焊缝的随机振动疲劳损伤，对比了两种方法计算的损伤值的差异。研究表明，CPM与FSSM相比，前者预测的损伤值大。