项目组合脆性风险的网络结构熵测度研究*
管杜娟,韩韵秋
(安徽建筑大学 经济与管理学院,合肥 230601)
随着项目组合中的项目数不断增加,项目组合呈现出规模大、工期长、复杂程度高以及不确定性强等特点[1-3]。复杂的内部结构,给项目组合的实施带来巨大的潜在危机,其中损失最严重的是导致整体失败的脆性风险[4-5]。因此,分析和测度项目组合的脆性风险,保障项目的顺利实施,是亟待解决的重要问题。
脆性是复杂系统的基本属性,国内外对于脆性风险的研究主要是基于复杂网络及复杂系统的脆性理论。有研究分析项目群网络拓扑结构与其脆性之间的关系,提出评估串联式和并联式项目群结构脆性的方法[6-7]。有研究应用脆性联系熵评价煤矿开采的脆性风险[8]。有研究结合脆性熵理论和集对分析方法,建立城市生态系统的脆性联系熵模型[9]。有研究应用脆性风险熵识别产品设计和制造模块中不确定性最大的关联模块,为优化设计网络提供依据[10]。有研究基于脆性风险熵提出一种量化制造设备脆性的方法[11]。
应用熵理论方法对项目组合的脆性风险进行度量,脆性风险熵将复杂系统看作一个整体,不考虑子系统之间的脆性影响。脆性联系熵基于对项目间脆性联系概率的测度,将项目间的脆性关联对系统整体崩溃的贡献率看作均匀的,项目节点对于项目组合系统整体崩溃事件的发生具有相同的重要度。然而,项目间的交互效应具有多种组合模式,受交互效应影响,项目间的脆性联系差异化明显,项目组合系统中可能存在的少数具有多重脆性联系的重要节点,也可能存在其他一些具有简单脆性联系的一般节点,由此决定了项目节点在脆性风险的传递中具有不同的重要度。因此,文中将网络结构熵应用于对项目组合脆性风险的度量,基于项目间的脆性联系概率计算项目节点的重要度,进而构建项目组合的脆性网络结构熵。
1 项目组合脆性网络结构熵构建
项目组合系统具有典型的非线性特征,项目之间的属性关联是非均匀的,单一项目在组合中呈现出不同的脆性结构特征,即可以找到少数与其他项目存在大量脆性联系的重要项目,也能够找到多数关联较少的普通项目。因此,项目组合脆性风险的测度和控制应重点关注具有较大脆性关联度的关键项目。
1.1 网络结构熵
复杂网络的非同质性决定了复杂网络中的节点连接是非均匀的。以万维网为例,具有中等连接和大量连接的节点占较少一部分,但是少量这样的节点却对整个网络结构起到主导作用。将具有这种特征的网络称为无标度网络,将这种性质称为复杂网络的无标度特性[12]。它体现了网络的非同质性,基于此,无标度网络中的节点不能被同等处理,少量具有大量连接的重要节点以及大量具有少量接连的末梢节点应该能够被识别和度量。
网络结构熵用来定量研究复杂网络的非同质性。网络结构熵应用节点的连接度测度节点在网络中的重要程度,节点重要度的定义为
(1)
式中:Ii为网络中第i个节点的重要度;Ki为第i个节点的连接度;N为网络中的节点数。网络结构熵被定义为
(2)
由式(2)可以看出,当各个节点的重要程度相同时,系统的网络结构熵是最大的,这就代表系统处于混乱无序的状态,反之,当网络中存在大量重要度低的节点以及少量重要度高的节点时,系统是相对有序的。因此,可以依据网络结构熵对复杂网络的无序程度进行度量,当定义节点之间的连接具有脆性特征时,网络结构熵的度量逻辑可以应用于对系统脆性崩溃总体不确定性的测度。
1.2 项目组合的脆性联系概率
由式(1)可知,网络中节点的重要程度由节点的连接度来测量。然而,对于不同关联程度的脆性连接,仅依据连接度的度量方法是不准确的,容易忽略掉连接度较低,而脆性关联程度较强的项目节点。因此,文中基于项目间的脆性联系概率测度项目的重要度,使之能够更加充分反映项目在脆性连接网络中的重要程度。
项目组合脆性联系概率的测度可以基于集对分析理论。假设X与Y是相互关联的两个项目,其中项目Y的状态由成本、进度、质量、预期现金收益和预期无形收益构成,记为yi(i=1,2,3,4,5)。当X项目失败,分析项目Y的状态的变动方向,当状态随着项目X的失败越来越差的时候,则yi与X之间存在脆性同一联系,反之,当状态yi随着项目X的失败变得越来越好时,则yi与X之间存在脆性对立联系,而当状态yi的变动方向无法判定或不受项目X失败的影响时,则yi与X之间存在脆性波动联系。
项目间的交互效应存在四种类型,即资源交互、技术交互、进度交互和收益交互,其中收益的交互效应还包括收益间共赢型的交互,即表现为两项目成果之间的互补,和竞争型的交互,即表现为两项目成果之间的相互替代[13]。项目X失败引起的项目Y的状态变化见表1。
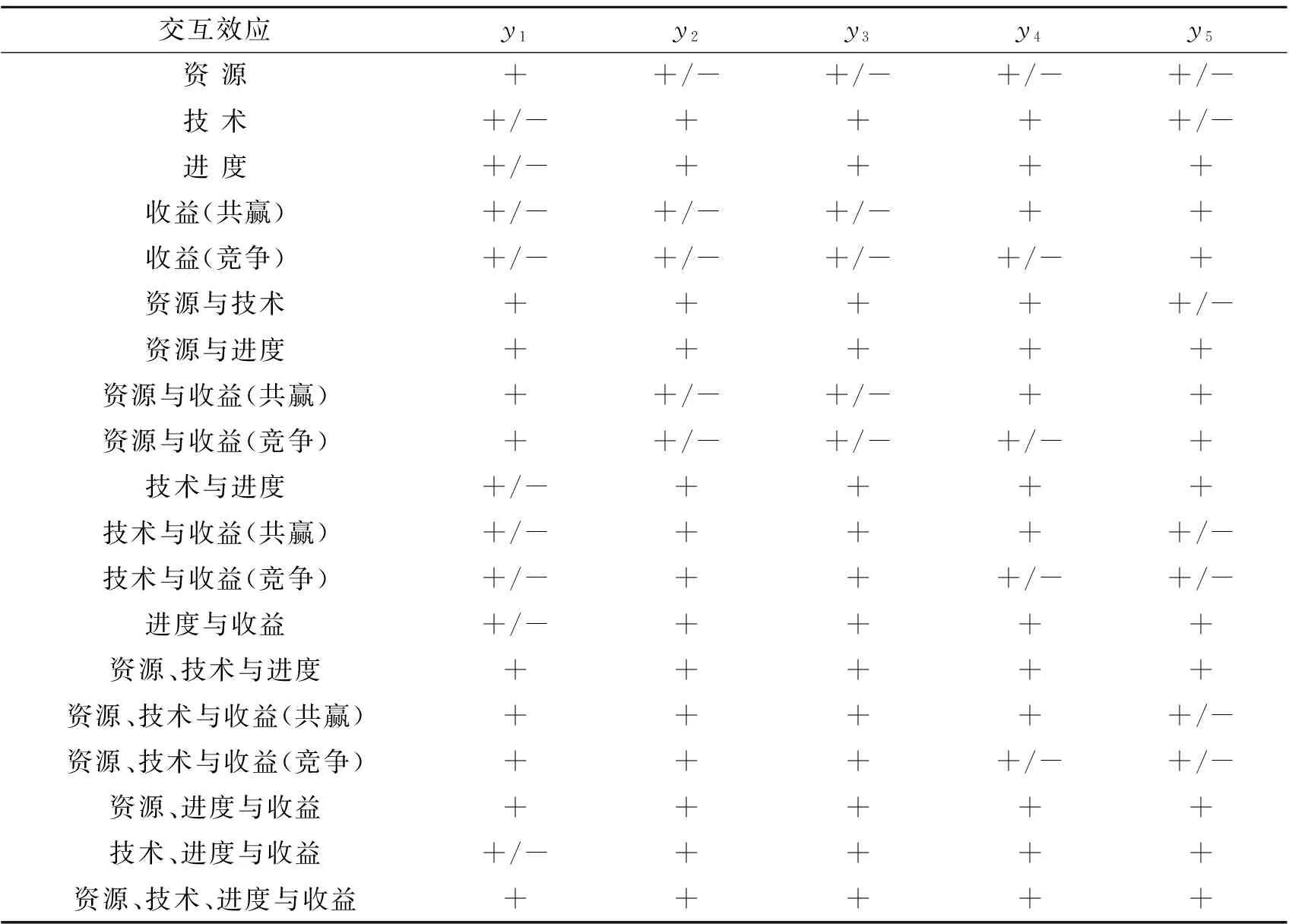
表1 不同交互效应下项目间的脆性联系状态
依据脆性联系状态,对应的脆性同一概率Pa(Y/X)、脆性对立概率Pb(Y/X)和脆性波动概率Pc(Y/X)的计算式为
(3)
其中n1,n2,n3分别为由项目X失败导致的项目Y的状态参数中脆性同一联系、脆性对立联系和脆性波动联系的个数。
脆性同一联系使得项目Y会受到项目X失败的消极影响,从而增加其失败的概率;脆性对立联系则使得项目Y能够抵抗项目X失败带来的负面影响,提高其成功的概率;脆性波动联系使得当项目X失败时,项目Y或不受影响,或增加其失败的概率,因此,测度项目组合的脆性联系概率为
Pij=ωaPa(Xj/Xi)-ωbPb(Xj/Xi)+
ωcPc(Xj/Xi),
(4)
式中:Pij为项目Xi失败导致项目Xi失败的概率;ωa,ωb,ωc分别为脆性同一概率、脆性对立概率和脆性波动概率对于脆性崩溃时间的贡献程度,其取值可由突变级数法确定[14],即
(5)
1.3 项目组合的脆性网络结构熵
根据网络结构熵的定义,需要首先算出节点的重要度。由于项目间脆性联系程度的不同,具有相同连接度的项目节点,其对脆性风险的贡献率有可能并不相同,因此,使用节点的连接度作为对其重要度的测度不能很好地反映项目间的脆性联系程度。计算测度项目组合系统中项目节点的重要度为
(6)
式中:Gi为项目Xi的脆性重要度;K为受到项目Xi失败影响的项目个数;N为项目组合中的项目总数。
基于对节点重要度的测度,可得项目组合的脆性网络结构熵为
(7)
由式(7)算得的脆性网络结构熵能够体现项目节点对其他相关项目的脆性影响程度,能够有助于识别少数的具有较大潜在脆性风险的项目节点,是对项目组合由系统脆性而引发整体崩溃的不确定性的总体测度。显然,项目间的脆性联系强弱分布的越不均匀,其总体不确定性越小,越容易控制,反之,在项目间的脆性联系程度均匀分布时,项目组合出现脆性崩溃的不确定性最高,控制性最差。
2 项目组合脆性风险度量
2.1 算例介绍
软件项目由于其在资源使用和技术研发等上的特殊性,为了实现企业利润最大化,多项目组合实施已经成为一种趋势。软件项目也因其在资源、技术等方面复杂的交互关系而使得其风险问题尤为突出,这导致项目的工期延长、成本增加,甚至无法正常实施。在前期研究过程中,对某商业银行的软件开发项目开展调研工作,文中选用该软件开发中心所实施的包含8个软件开发项目的项目组合案例,项目间的交互关系见表2。
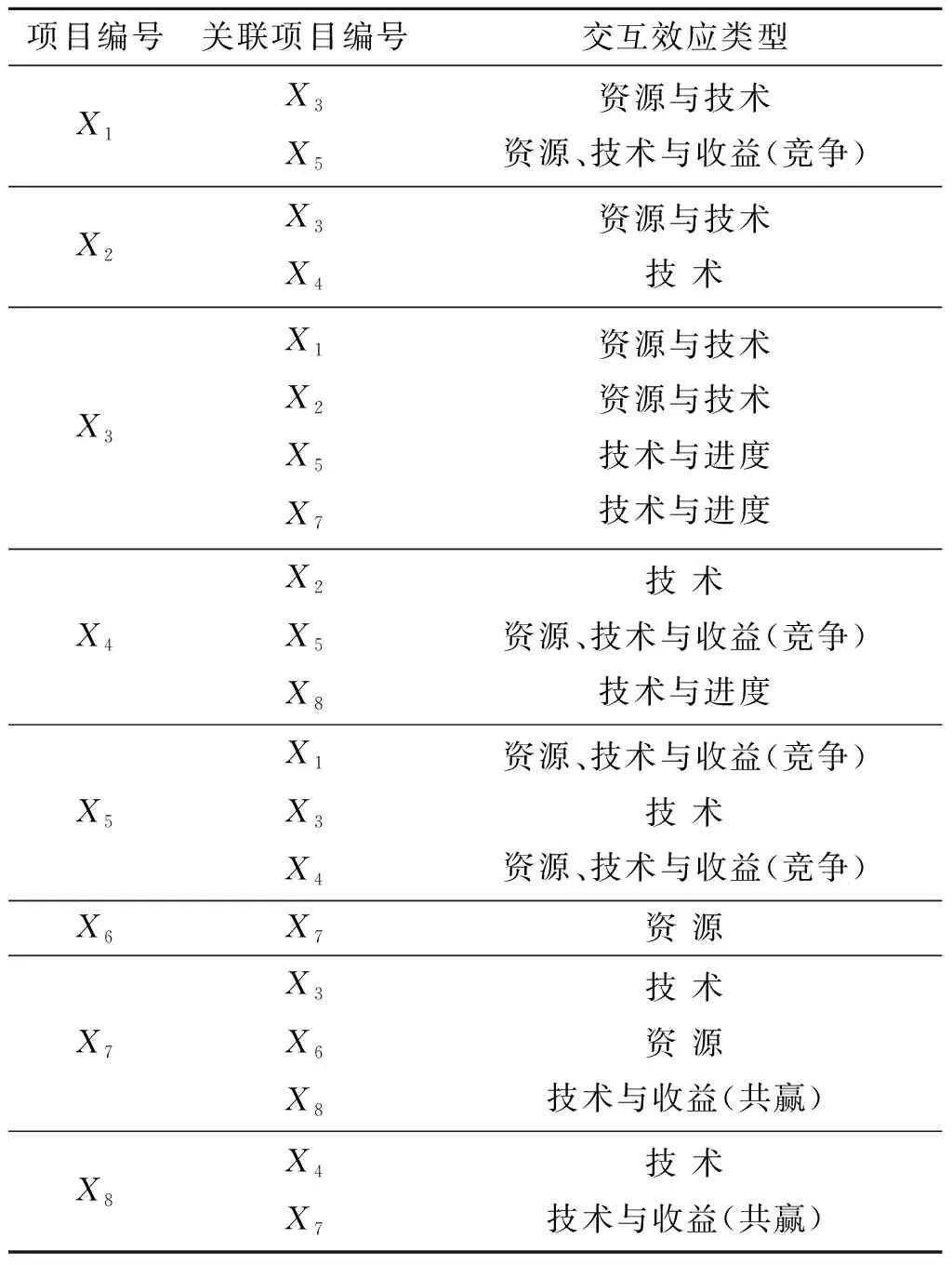
表2 脆性关联项目信息表
需要指出的是,进度交互是一种单向的交互效应,如表1中给出的,项目X3对项目X5存在技术和进度上的交互效应,这说明X3项目是项目X5的上游项目,它的研发成果或中间结果可以构成项目X5的一个研发输入,但是,反之不存在这样的影响,即项目X5作为下游项目,其成功与否,从进度上来说对于项目X3没有影响,因此项目X5对项目X3只存在技术交互效应上的影响。
2.2 模型计算与结果讨论
模型计算的过程主要步骤为:依据表2所列的项目间交互关系的类型,对应表1得出各种关系下的脆性联系状态,其代入式(3),得到每种关系下的脆性同一、脆性对立和脆性波动联系出现的概率;通过应用式(4)和权重计算式(5),算得每种交互关系所对应的脆性联系概率见图1;由式(6)得项目组合中各项目节点的脆性重要度见表3;由式(7)算得该项目组合的脆性网络结构熵为2.016 6。
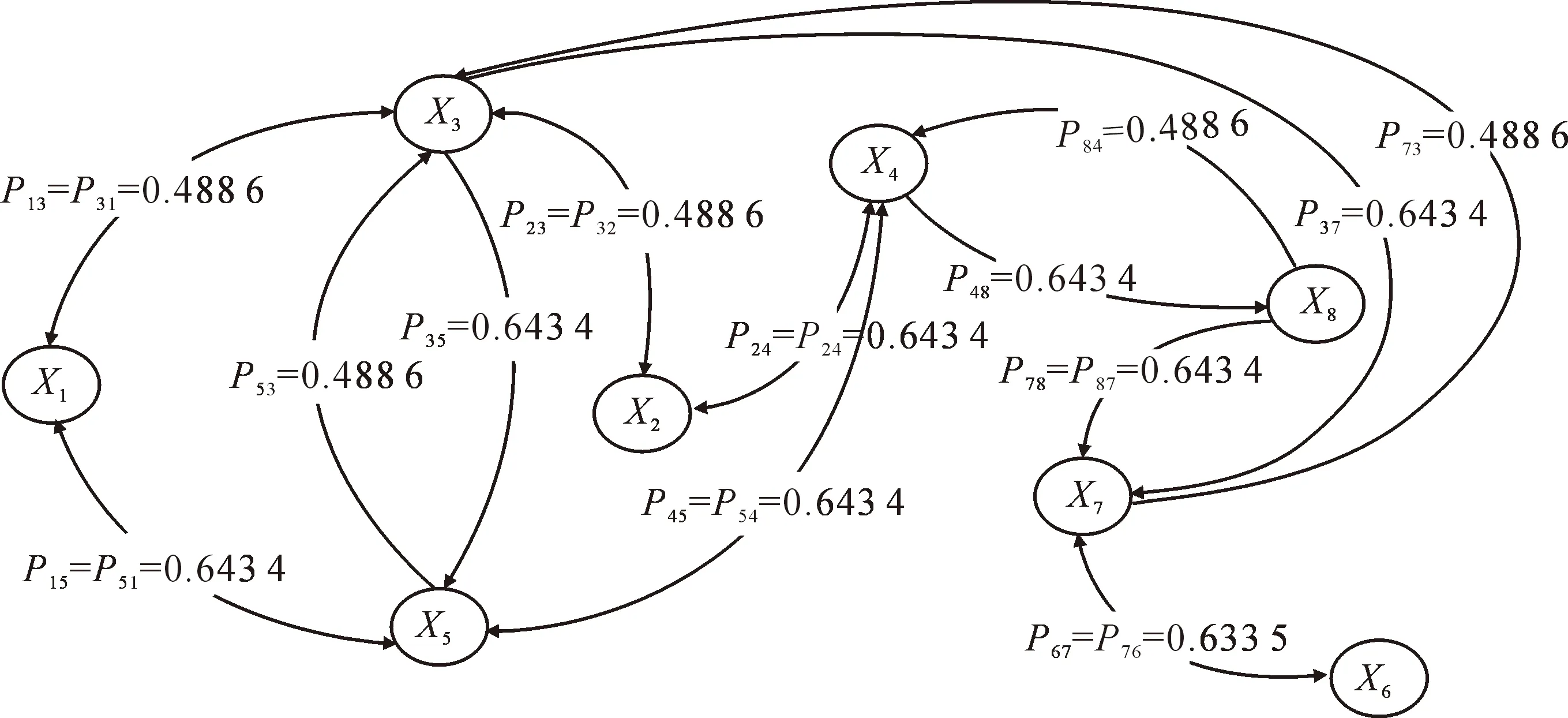
图1 项目组合脆性联系网络Fig.1 Brittle connection network of project portfolio
在当前节点总数下,当脆性联系概率均匀分布时其总体崩溃的不确定程度是最高的,此时其脆性网络结构熵为2.079 4,可见该项目组合因某项目失败而导致整体失败的总体不确定性是非常高的。由表3可以看出,项目的重要度最高,凡是超过均匀分布时的节点重要度的项目X3节点都应作为关键项目加以监控,即项目X4、项目X5和项目X7被认为是脆性高危节点。
对比脆性联系熵和脆性风险熵,前者只能算得项目之间关联的不确定性,后者的测度还需要对单一项目的失败概率进行估计,且不能反映节点之间的重要性差异,无法识别脆性崩溃路径上的关键项目,对管理实践的指导意义较低。
为了验证结论的可靠性,应用图理论对脆性结构网络进行分层,识别具有脆性全连通影响的脆性源项目,以及其他层级上的关键项目,评价项目组合的脆性风险。
由图1可得该项目组合所对应的邻接矩阵M,为避免全连通的结果,提升分析的显著性,对于矩阵M的元素mij处理为
(8)
处理后得邻接矩阵M为

计算邻接矩阵M的可达矩阵,得
(M+I)5=(M+I)6=

由可达矩阵可以得出项目组合脆性风险传播过程中,每个项目节点的可达集和先行集见表4。
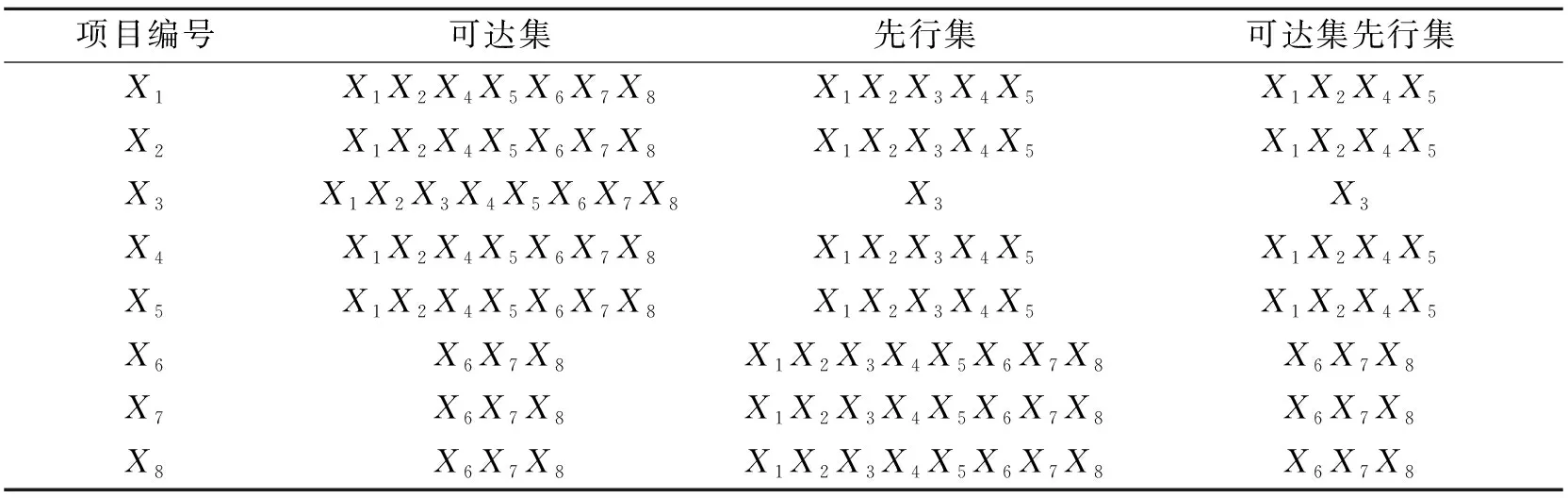
表4 项目节点脆性风险传播的可达集和先行集
按照可达集∩先行集=可达集的原则,首先得出最高层节点,划去对应的行和列,用同样的方法继续确定下一层节点,直到所有节点都被归入相应的层级,最后得出该项目组合的分层情况如图2所示。
由图2可知,项目组合脆性联系网络存在3个层级,项目X3位于最低层级,是与所有项目节点全连通的脆性源项目;项目X1、项目X2、项目X4和项目X5位于中间层级,其中项目X5是X3与中间层级之间的关键连通项目;项目X6、项目X7和项目X8位于最高层级,其中项目X7与脆性源项目连通,项目X8与位于中间层级的项目X4连通。项目组合脆性风险的传播是由脆性源项目开始,通过层级间的关键连通项目遍历到全局,最终导致项目组合的整体失败。对于该项目组合,脆性崩溃有两条路径,一是由脆性源项目X3出发,通过项目X5和项目X7并行影响中间层和最高层项目节点,导致全面失败;二是由脆性源项目X3出发,首先通过项目X5影响中间层项目节点,再经由项目X4将脆性风险传播至最高层项目。这与表3中所得的结论基本相符。
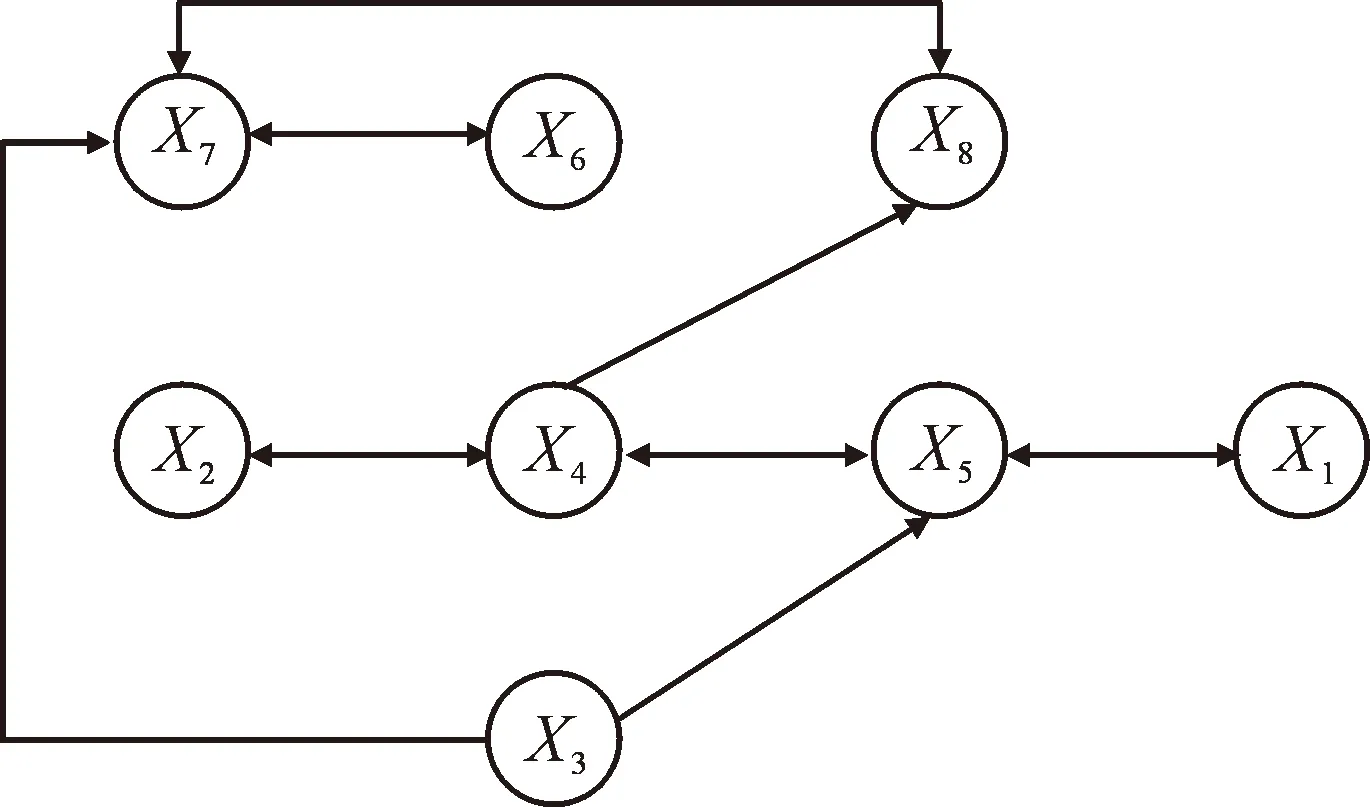
图2 项目组合脆性联系网络层级图
脆性重要度最高的项目X3是脆性源项目,脆性重要度较高的项目X4、项目X5和项目X7被近乎均匀的分布在了其他两个脆性联系层级,因此该项目组合的脆性网络结构熵是较高的,这意味着该项目组合具有较高的脆性风险。
3 结 语
文中针对项目在组合中的异质性问题,提出一种基于改进的网络结构熵测度项目组合脆性风险的方法。该方法能够反映网络中少数具有大量连接的项目节点在网络中的重要作用,从而避免脆性联系熵和脆性风险熵无法表现节点之间异质性的弊端。对网络结构熵计算节点重要度的方法进行了改进。通过计算不同交互效应影响下节点间的脆性联系概率测算项目节点的重要度,充分考虑了脆性风险在项目间传播的非均匀性,弥补了根据节点连接度计算节点重要度,以致将各种连接视为同质的缺陷。为验证模型的有效性和合理性,基于算例得出模型对于项目节点的重要性排序及脆性关联影响,与图模型系统分层理论的分析结果相吻合。项目组合实施中,可针对节点的重要性排序及关联路径设计风险防控策略,动态监测网络结构熵的变化,及时对项目间的脆性关系进行调整,增强项目组合脆性风险的可控性,降低实施整体失败的风险。

