基于R/S分析的大藤峡出山径流灰色预测

崔延华，王 理，吴文强

(1.广西大藤峡水利枢纽开发有限责任公司，广西 南宁 530000；2.水利部珠江水利委员会水文局，广东 广州 510611；3.中国水利水电科学研究院，北京 100038)

人类对水文过程的研究由来已久，随着人类活动轨迹的扩展和科技水平的提高，不断增加着新的内容[1]。河川径流量是水资源综合开发利用、科学管理和优化调度最重要的依据[2]，河川径流的演变是水文学的重要研究内容[3]。径流量的科学预测对地区水资源合理分配和社会-经济-生态可持续发展具有重要作用[4]。径流变化也具有明显的灰色特征[5]。在中国，将灰色理论应用于河流径流量的预测开始于20世纪80年代，至今该理论的应用已经相当成熟[6]。李建林等[7]基于灰色预测模型对黑河出山年径流量进行了灰色预测。陈立华等[8]运用RVA法分析黔江中游水文情势变化特征。目前,针对大藤峡出山径流预报的研究较少，原因是大藤峡水利枢纽工程是国内在建大型水利工程，兴建时间晚，相关研究尚未涉足或正在开展，资料收集和数据分析需要时间过程。但是大藤峡水利枢纽工程作为黔江流域控制性水利工程，大藤峡出山径流预报及预测精度准确性都对大藤峡水利枢纽工程水情预报与水库调度具有重要意义。基于此，为了填补大藤峡出山径流预报研究空白，本文利用R/S分形分析法能够通过改变研究对象的样本序列周期长度，有效解决样本序列随时间推移波动性大问题的优点，将灰色预测模型与R/S分形分析法有效结合起来，预测大藤峡出山径流量V，通过构建R/S-灰色预测模型并对大藤峡出山径流量V的预测结果及模型预测精度进行对比分析，同时对灰色预测模型与R/S分形分析法在大藤峡出山径流演变规律及未来预测中的适用性进行分析讨论，研究结果对大藤峡水利枢纽工程水情预报与水库调度具有一定的参考价值。

1 研究方法

1.1 GM(1,1)模型

运用GM(1,1)模型可以对所研究时间序列对象的演变规律进行系统分析，并对其未来变化趋势做出中长期预测。基于此，本文建立灰色系统GM(1,1)模型[9]。

设原始时间序列为：

X(0)(k)={x(0)(1),x(0)(2),…,x(0)(n)}

(1)

对X(0)(k)作一次累加计算，得到：

X(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)}

(2)

则GM(1,1)模型的微分方程为：

(3)

运用最小二乘法计算得出GM(1,1)模型参数a、u，即：

(a,u)T=(BTB)-1BTY

(4)

离散化所研究时间序列对象函数，进而对式(3)求解得：

x(1)(k+1)=[x(0)(1)-u/a]e-ak+u/a

(5)

经过累减还原计算可得出其原始时间数据序列的估计值：

(6)

设大藤峡出山径流量V实测序列见式(1)，其对应的预测序列为：

(7)

则平均相对残差值为：

(8)

精度为：

(9)

如果精度P≥0.8，说明模型精度满足要求，反之要对模型进行优化[10]。

1.2 R/S分析

R/S分析法也被称为分形时间序列[11-12]。本文运用R/S分形分析法计算得出Hurst指数，进而判定大藤峡出山径流量V和时间序列的平均循环周期T。分形时间系列满足：

R(n)/S(n)=(an)H

(10)

式中R(n)/S(n)——重标极差；n——增量区间长度；a——常数；H——Hurst指数[13]。

具体计算步骤如下。

步骤二计算Dm(n个期间)的累积离差Xk,m。

(11)

步骤三由Xk,m算出Dm的极差Rm，以及其对应的标准差Sm。

步骤四Dm的重标极差通过式(12)计算得出：

(R/S)m=Rm/Sm

(12)

步骤五对每个连续大藤峡出山径流量V子时间序列，重复式(10)—(12)，则该连续大藤峡出山径流量V子时间序列的重标极差为：

(13)

步骤六要求n≥3，且n为3的倍数，时间序列{x(k)}符合式(10)要求，进而得到式(14)：

lg(R/S)n=Hlga+Hlgn

(14)

Hurst指数H的有效值范围介于0～1[14]。为了定量表征大藤峡出山径流量V时间序列的平均循环周期T，引入统计量Q(n)：

(15)

Q(n)随Hurst指数H的变化而变化。Q(n)-lgn关系曲线图上的拐点n就是大藤峡出山径流量V时间序列的平均循环周期T。

1.3 R/S-GM(1,1)模型

长时间序列存在波动性问题，运用R/S-GM(1,1)模型处理波动性问题[15]，步骤如下。

步骤一截取大藤峡出山径流(T-1)年数据作为初始值，标记为Q={q1,q2,…,qT-1}。以时间序列Q为基础建立GM(1,1)模型。如果GM(1,1)模型精度P>80%，则预测模型的残差检验结果满足要求；否则，要求对GM(1,1)模型进行优化，使得P>80%；以下预测步骤都需要进行模型精度的检验。

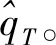
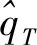
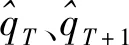
步骤五按照步骤得出大藤峡出山年径流T年预测值。

运用式(1)—(6)进行预测，运用式(7)—(9)进行验证。

2 研究区及数据来源

2.1 研究区域概况

大藤峡水利枢纽位于珠江流域西江水系的黔江河段大藤峡谷出口的弩滩处，地理坐标为东经110°02′，北纬23°28′。坝址在北江桥上游6.6 km处。坝址以上控制流域面积为198 612 km2。大藤峡坝址以上流域近似呈东西向矩形，地势呈西北高东南低，平均海拔高度约为1 450 m。坝址以上河流自西北向东南方向流动。黔江段河道狭窄弯曲，黔江流经武宣盆地，自勒马始，河流切割大瑶山形成著名的40多公里的大藤峡，峡谷两岸山高坡陡，坡降为0.5‰～0.6‰，河床纵剖面起伏剧烈，个别地点江底高程低于珠江基面零点以下50余米。黔江出大藤峡谷后进入丘陵平原地带。

2.2 数据来源

本研究的径流资料采用桂平水文站1932—2021年逐年径流量，并对上述资料进行了复核，结果表明各站资料基本合理，可以采用。大藤峡出山径流1932—2021年逐年实测径流量V序列见图2。从图2可知，大藤峡出山径流1932—2021年逐年实测径流量V序列的总体特征为：大藤峡出山径流V在长期变化中呈现缓慢下降趋势，大藤峡出山径流V的变化幅度随时间变化较为明显。

3 结果分析

运用灰色模型，对大藤峡出山径流1932—2021年共计90年的逐年实测序列进行预测分析。

3.1 径流量的GM(1,1)灰色预测模型

首先，运用式(1)—(9)取大藤峡出山径流1932—2015年的逐年实测数据构建大藤峡出山径流V的GM(1,1)预测模型，模型建立结果见表1。其中大藤峡出山径流V为x1(0)。

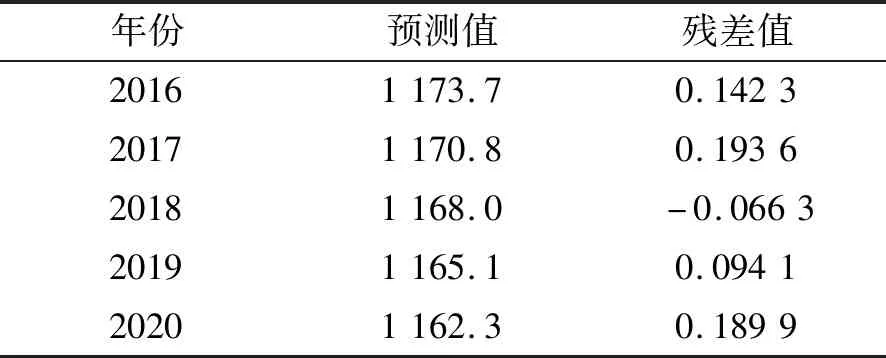
表1 GM(1,1)模型的大藤峡出山径流V预测结果 单位：亿m3

累加大藤峡出山径流量x1(0)得出累积大藤峡出山径流量x1(1)，把累积大藤峡出山径流量x1(1)代入式(3)求得a=-0.002 4，u=1 443.303，其中a为发展系数，u为灰作用量，进而将时间响应函数离散化，利用初始条件对式(3)求解得：

(16)

经累减还原可得大藤峡出山径流量V数据序列的估计模型：

(17)

式中，k=1,2,…,n-1。

根据式(6)预测2016—2020年的逐年大藤峡出山径流量V，其预测值见表1。由式(8)计算大藤峡出山径流量GM(1,1)模型的平均相对残差值，逐年残差值见图3，大藤峡出山径流量GM(1,1)模型平均残差值为0.156 2，则模型精度是84.38%；由表1可以看出，GM(1,1)模型的预测精度是86.28%，均大于80%，达到了灰色模型建立标准，预测效果良好。

3.2 径流量的R/S模型分析

本文统计了大藤峡出山径流1932—2021年逐年实测径流量V序列，并对之进行变化趋势分析。运用R/S模型方法分析大藤峡出山径流V的平均循环周期T。

分别取n为3、5、6、9、10、15、18、30、45，依照式(10)—(14)对大藤峡出山径流V序列进行分析计算，得到lgn与lg(R/S)的拟合关系，见图4。

由图4可以得出lg(R/S)与lgn之间的关系式为：lg(R/S)= 0.8049lgn-0.624,其中相关系数R2=0.988 9。因此，大藤峡出山径流V序列的Hurst指数为0.804 9。H明显大于0.5，这表明大藤峡出山径流V序列为分形时间序列，其持续性和记忆性表现显著。根据式(10)—(14)对大藤峡出山径流V序列进行分析计算，得到lgn与lg(R/S)的拟合关系(图4)。

由图5可知：Q(n)-lgn关系曲线的趋势性在箭头所指处发生突然转折，由拐点之前的上升趋势突变为下降趋势，而拐点处横坐标所对应的时间长度n即为大藤峡出山径流V序列的平均循环周期T。即大藤峡出山径流V曲线图上的拐点n就是大藤峡出山径流量V时间序列的平均循环周期T。大藤峡出山径流V序列在n=9时(箭头所指处)出现一个突变点，这表明大藤峡出山径流V序列的平均循环周期T=9。T反映了初始条件对大藤峡出山径流V序列产生影响的平均循环周期长度，换言之，T表征了大藤峡出山径流对初始条件的平均记忆长度，在9年后初始条件对大藤峡出山径流V序列的影响作用将完全消失。

3.3 径流量的R/S-GM(1,1)模型

R/S-GM(1,1)模型就是将R/S分形分析的结果应用到GM(1,1)预测模型中，即在一个循环周期T内进行大藤峡出山径流量V的GM(1,1)模型预测，以减少由于时间序列的波动性引起的误差。大藤峡出山径流V的平均循环周期T为9a，因此，本文选取2008—2015年共计8a大藤峡出山径流量V作为基础数据，利用1.3节中的计算步骤，建立大藤峡出山径流V的R/S-GM(1,1)预测模型，并对其进行精度验证，预测结果见表2。

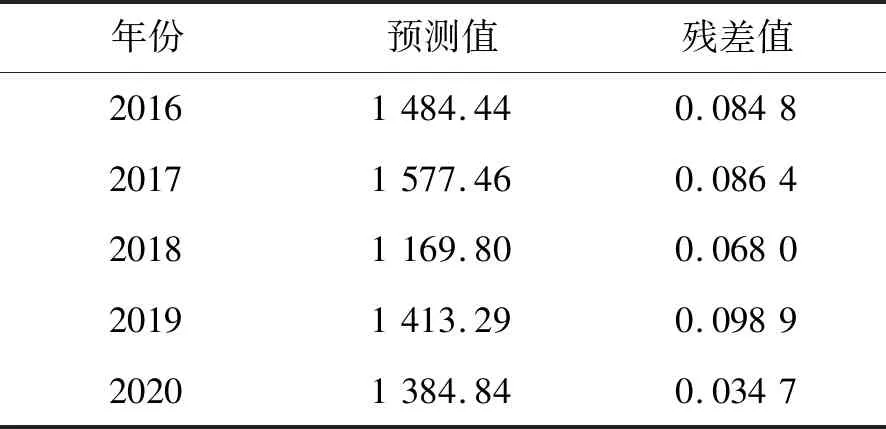
表2 R/S-GM(1,1)模型的大藤峡出山径流V预测结果 单位：亿m3

由表2可以看出，大藤峡出山径流量R/S-GM(1,1)模型的模型精度为87.46%，该模型的预测精度为92.54%，R/S-GM(1,1)预测模型的精度大于90%，根据灰色模型精度检验等级，精度大于90%即为优秀，因此，R/S-GM(1,1)预测模型不仅通过了残差检验，达到了灰色模型建立标准，而且模型预测精度优秀。

3.4 模型预测精度对比

由表3知，GM(1,1)模型和R/S-GM(1,1)模型的模型精度分别为84.38%和87.46%，预测精度分别为86.28%和92.54%，后者的模型精度和预测精度均高于前者。分析讨论如下。

表3 不同模型的大藤峡出山径流V预测精度对比 %

a)GM(1,1)模型以1932—2015年的实测大藤峡出山径流V为基础进行建模，由于所选取的大藤峡出山径流原始数据序列时间跨度相对比较长，其带来的波动性也相对比较大，因此影响GM(1,1)模型的模型精度和预测精度。

b)对比GM(1,1)模型，R/S-GM(1,1)模型第一步运用R/S分形分析得出大藤峡出山径流序列的平均循环周期T等于9年，第2步选取连续9 a的实测大藤峡出山径流V序列作为原始数据，在9 a的大藤峡出山径流序列基础上建立R/S-GM(1,1)模型，这样做的好处是使得大藤峡出山径流序列的时间跨度大幅减小，进而导致大藤峡出山径流序列的波动性也随之大幅降低，此外，R/S-GM(1,1)模型运用递补法，在建立模型过程中用大藤峡出山径流量的预测值代替实测值，目的是减缓大藤峡出山径流序列的波动性，以上步骤提高了R/S-GM(1,1)模型的预测精度，使之高于GM(1,1)模型。该R/S-GM(1,1)模型的优点是有效合理减小研究对象的序列长度，从而降低序列的波动性。综上所述，R/S-GM(1,1)模型在GM(1,1)模型基础上进一步提高了模型精度和预测精度。R/S-GM(1,1)模型适合用于预测未来中长期的大藤峡出山径流量。

4 结论

大藤峡水利枢纽工程是红水河综合利用规划中最末一个梯级，也是黔江干流乃至整个黔江流域唯一的水利枢纽，距离上游干流最近的桥巩电站212 km，天然河道长，受上游电站人为调控影响较小，自然因素影响较大。因此，本文采用灰色理论模型方法，根据实测的大藤峡出山径流量V序列建立灰色预测模型，结果表明，大藤峡出山径流量V时间序列的分形特征表现显著，对大藤峡出山径流量V时间序列而言，R/S分形方法是一种有效的分析方法，R/S分形分析法中的2个重要参数是平均循环周期T和Hurst 指数H。Hurst指数H的作用是判定大藤峡出山径流量V时间序列的状态特性和分形结构，平均循环周期T的作用是检验R/S分形分析法在使用过程中的稳定性，判断大藤峡出山径流V序列的平均循环周期T是否存在，并据此估计平均循环周期T的长度。大藤峡出山径流V时间序列的灰色特征表现显著，在大藤峡出山径流量的预测过程中，GM(1,1)模型的模型精度是84.38%，预测精度是86.28%；而在GM(1,1)模型的基础上先进行R/S分形分析，再判定出大藤峡出山径流序列的平均循环周期是9 a，基于此构建的大藤峡出山径流量R/S-GM(1,1)预测模型，其模型精度为87.46%，预测精度为92.54%，R/S-GM(1,1)模型相较于GM(1,1)模型的优点是有效合理减小了研究对象的序列长度，从而降低了研究对象序列的波动性。R/S-GM(1,1)预测模型为大藤峡出山径流量的中长期预测提供了一种新的方法。