超音速圆柱射弹斜入水流固耦合数值计算

张硕,胡明勇,孟庆昌,易文彬

(海军工程大学 基础部，武汉 430033)

射弹入水问题作为超空泡问题中的一个典型问题，是一个复杂的多相耦合动力学问题，超音速射弹入水时，流体可压缩性对空泡演化过程的影响、射弹运动对流体动力学特性的影响等是入水问题的难点。学者们的研究为通过ESI-CFD构建非结构化网格，仿真计算射弹头部形状对超空泡流动的影响；利用动网格技术，并通过嵌入用户自定义函数的方法得到高速射弹垂直入水时的空泡演化与闭合等规律；基于多物质的任意拉格朗日-欧拉-拉格朗日流体与固体耦合算法，得到了射弹初始入水速度对空泡面、空泡深闭合时间的影响规律以及射弹加速度、应力、应变响应；通过Ansys fluent模拟二维情况下射弹以多角度高速入水过程，得到了不同角度下弹体入水空泡形态发展规律、弹道特性及流体动力特性变化规律。

在此基础上，针对超空泡射弹入水问题，考虑基于流体体积多相模型和流体结构相互作用模型，结合STAR-CCM+软件的重叠网格技术，建立亚音速斜入水计算模型，完成超空泡射弹超音速入水流固耦合计算，分析了射弹长径比和入水速度对超音速射弹入水过程的空泡演化、流场压强变化的影响规律以及射弹的速度、载荷和应力的影响规律。

1 数学模型

对弹体入水过程中的流场进行计算，流场除需满足连续性方程外，还需满足质量和动量守恒方程。

1)质量守恒方程。

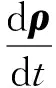
(1)

式中:、、分别为容量、转换和散度矩阵;为材料密度；为时间。

2)动量守恒方程。

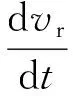
(2)

式中：和分别为广义质量和传递矩阵;为对应于参考构型描述下的速度;和分别为内力和外力向量。

为简化计算，提高模型收敛性和计算精度，建立用户自定义流体密度模型：

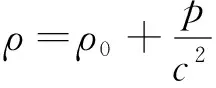
(3)

其中:为水的实际密度;=998.2 kg/m为水的参考密度；为水的实际压力；为水中的声速。

计算采用SST K-Omega湍流模型，该模型结合了K-Omega湍流模型近壁稳定性和K-Epsilon 湍流模型边界层外部独立性的优点。

2 弹体斜入水数值计算与实验

2.1 模型参数

弹体为圆柱体，空化器直径=14.5 mm，模型长度分别为72.5、108.75、145 mm。射弹材料采用铝合金，密度为2.734×10kg/m，相关参数见表1。

表1 铝合金平头圆柱体弹体数据

2.2 实验设备与数据处理

射弹亚音速入水实验基于亚音速射弹小尺度模型入水实验系统展开，该系统主要由一级气体炮发射系统、高速摄影系统、水箱3部分组成，发射管材料为304不锈钢，长2 m、直径15 mm，高压气瓶最大可提供6 MPa气压，通过调节不同的初始气压来调节弹体的初速度，入水水箱尺寸长、宽、高为2.0 m×1.0 m×2.0 m。使用Phantom Camera v611型高速摄影机进行高速摄影，高速摄影机最大帧数为11 000 帧/s。使用Phantom摄像机控制软件(PCC)控制摄影机摄录和对视频进行后处理。一级气体炮发射系统、高速摄影系统、水箱、射弹入水图见图1～4。

图1 一级气体炮发射系统

图2 高速摄影系统

图3 水箱

图4 射弹入水图

为便于数据处理与分析，采用空化器直径对入水深度进行量纲一的量化处理。

(4)

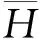
在超音速射弹入水问题中，马赫数能够更清晰地反映射弹的速度变化规律，定义为

=

(5)

式中:为入水速度;=340 m/s为声音在空气中的传播速度。

定义量纲一的量空泡直径与量纲一的量空泡长度为

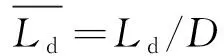
(6)

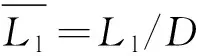
(7)

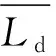
定义轴向力系数为

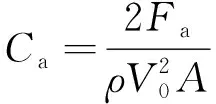
(8)

式中:为轴向力；ρ为流体密度；为射弹初始入水速度；为射弹截面积，=1.651 3×10m。法向力系数使用相同方法处理。

2.3 网格划分

为消除网格质量和数量对计算结果带来的误差，需进行网格无关性验证。建立3种不同网格密度的网格，对初始入水速度为59.2 m/s的5射弹进行仿真计算，网格数见表2。

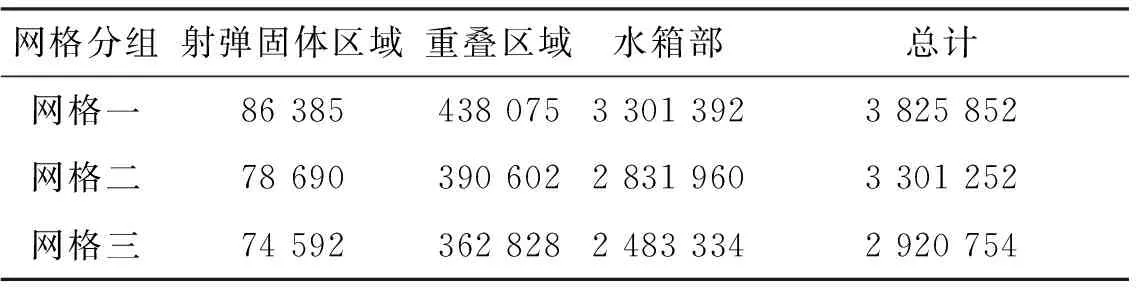
表2 网格数

随网格密度的增加，相同时间下入水距离差值最大为0.000 67 m,误差为0.17%。最大误差小于仿真允许误差5% ，满足网格无关性要求。考虑射弹高速入水的仿真精度和计算时间成本，选取网格二进行计算。

分域模型见图5,流体部分由水相、气相构成。空气域长宽高尺寸为42×14×14，水域长宽高尺寸为42×14×28。

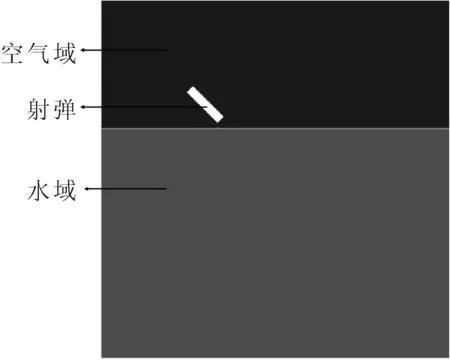
图5 分域仿真模型

网格划分见图6，在水域与空气域的交界处和射弹运动路径周围进行加密处理。

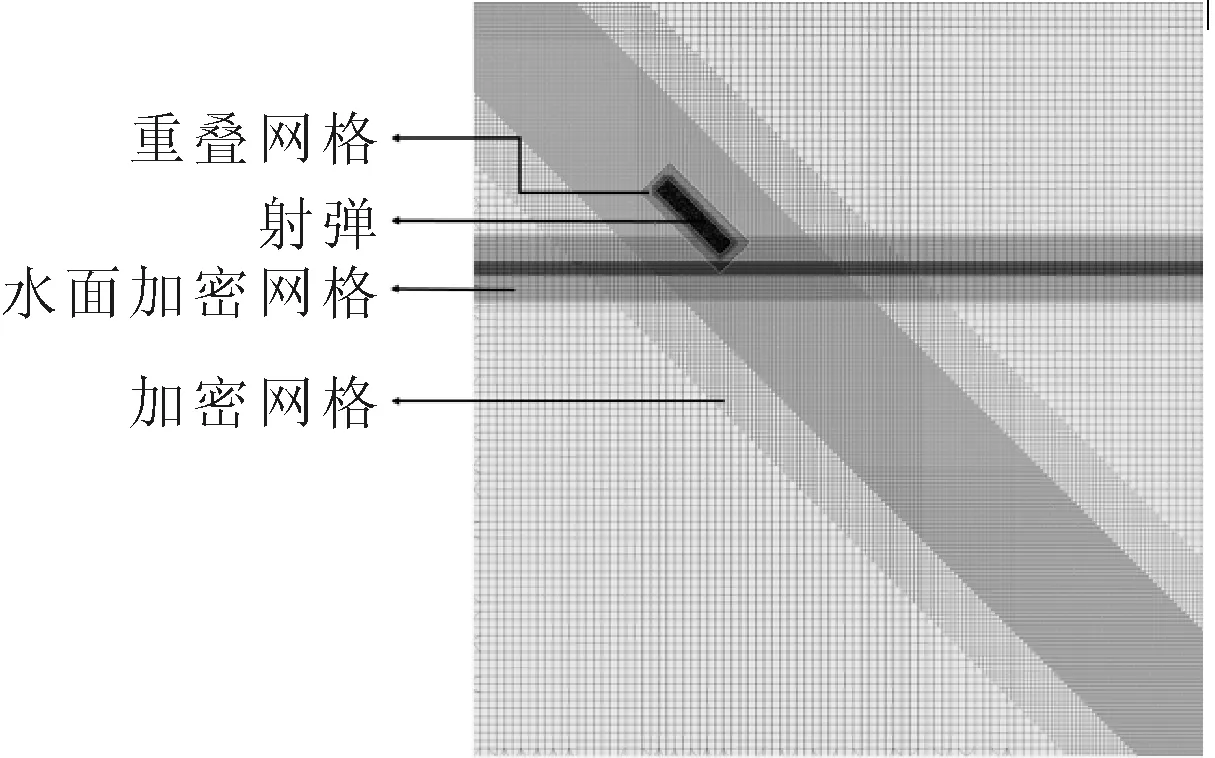
图6 网格划分

2.4 物理模型与边界条件

选择VOF模型。水位点为射弹头部中心处向下0.01 m处，水面垂直方向为竖直向上。

选择流体结构相互作用模型(FSI)以解决固体和流体相互耦合的强耦合问题，通过为射弹创建一个固体区域，为射弹周围的流体创建一个流体区域的方式，同时对结构和流体求解，并在流体结构交界面上进行数据交换。

2.5 数值计算结果与实验对比

以5D射弹为例验证算例的准确性，初始入水速度参数见表3。

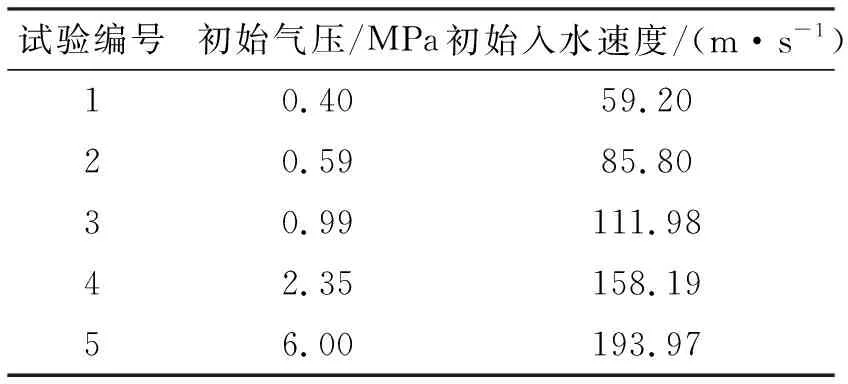
表3 初始入水速度参数

射弹在不同初始速度下量纲一的量入水深度随时间的变化见图7。将计算结果与实验数据进行比较，误差最大为7.22%。射弹在不同初始速度下入水速度随时间的变化见图8。将计算结果与实验数据进行比较，误差最大为13.9%。随入水速度增加，相对误差逐渐变小，计算与实验结果吻合程度较好，说明本文算法准确。

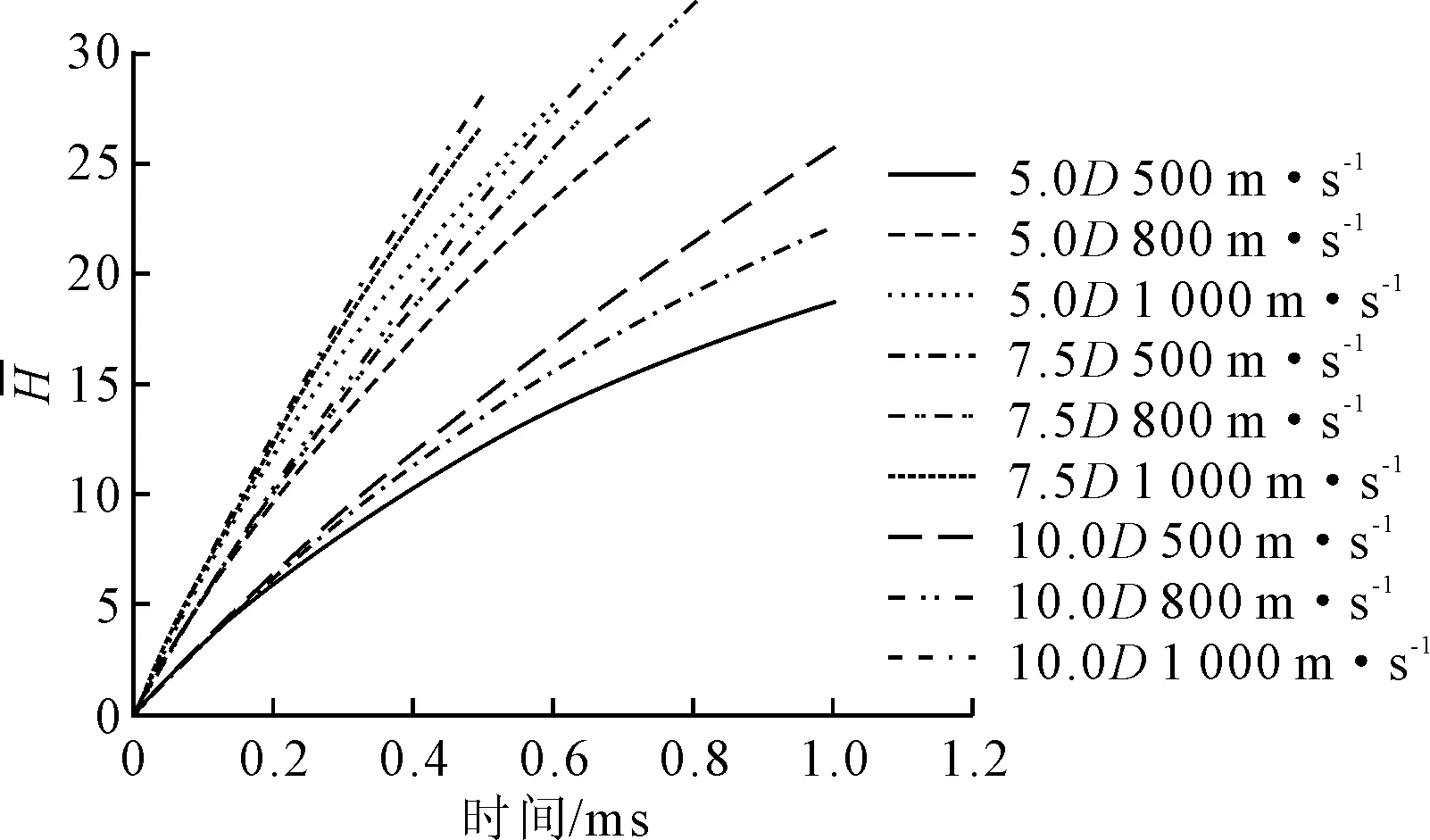
图7 入水深度对比

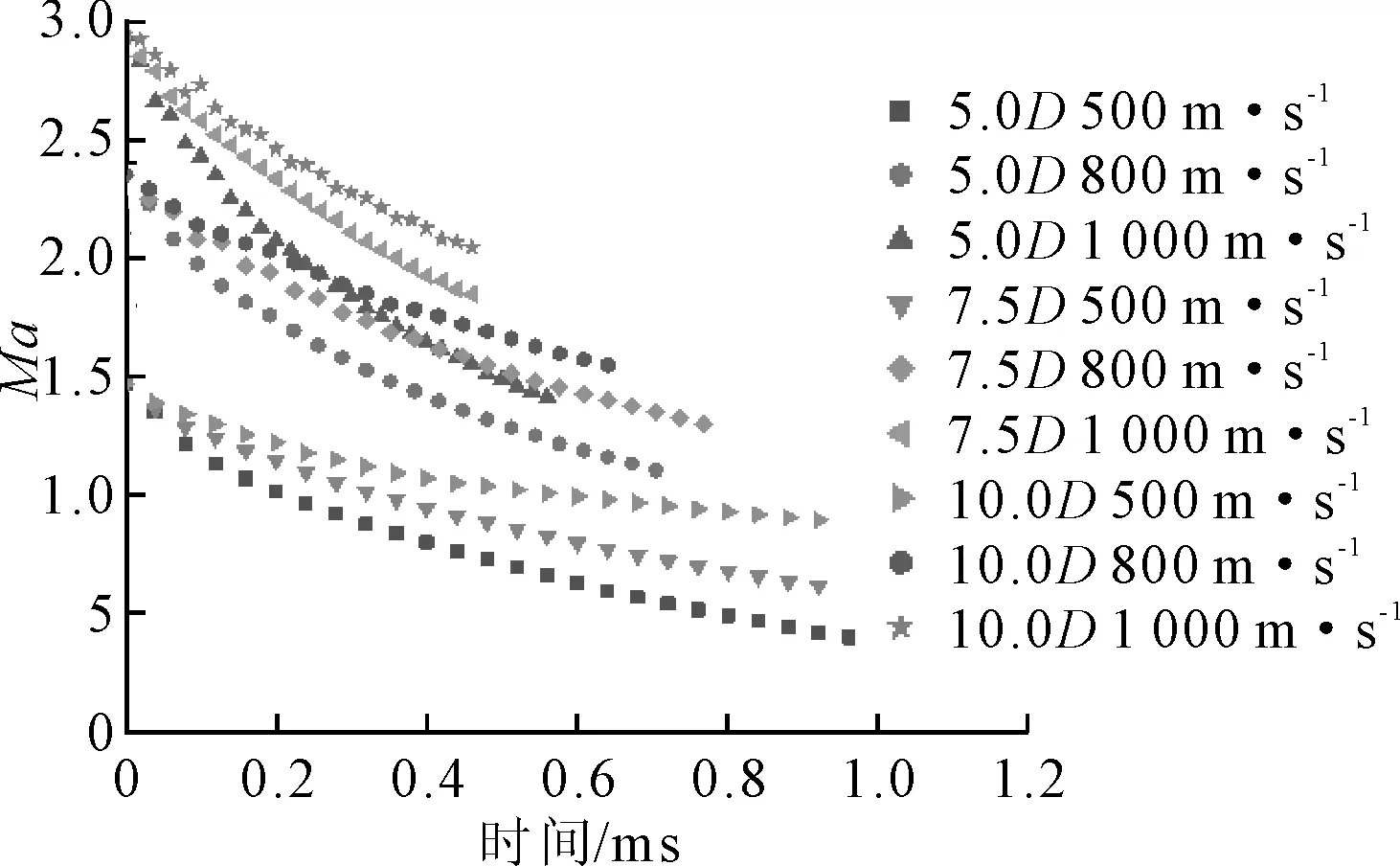
图8 入水速度对比

3 弹体高速斜入水流固耦合数值计算

3.1 运动特性分析

初始相同时，在同一入水时间，长径比越大，量纲一的量入水深度越大。长径比相同时，在同一入水时间，初始越大，量纲一的量入水深度越大。初始相同时，长径比越大，衰减越慢。这是因为长径比大的射弹质量更大，动能更高，存速性能更好。

3.2 阻力系数变化规律分析

不同长径比射弹在不同初始下轴向力系数和法向力系数随时间的变化见图9、10。

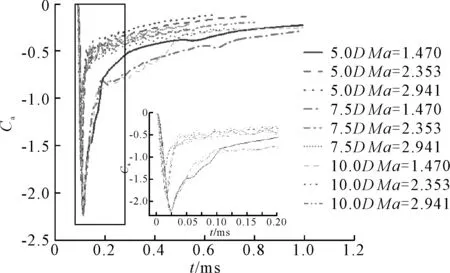
图9 轴向力系数随时间变化

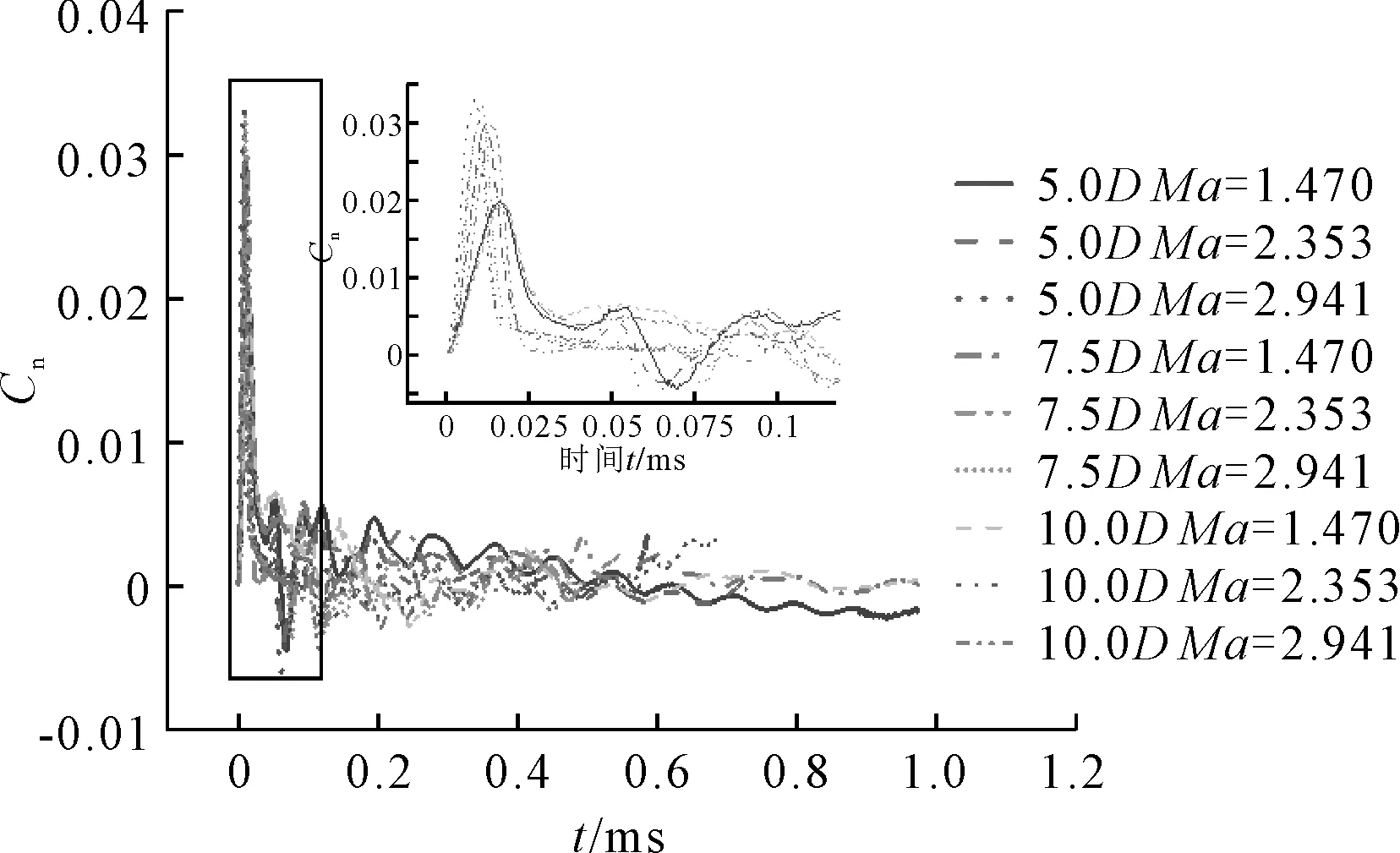
图10 法向力系数随时间变化

由图9、10可知，射弹抨击自由液面瞬间，轴向力系数和法向力系数达到峰值，相同初始下，长径比越大，轴向力系数和法向力系数最大值越大。射弹入水后，轴向力系数和法向力系数迅速下降，且不同长径比射弹轴向力和法向力变化趋势相似。此时，法向力系数在0附近周期波动，且波动幅度越来越小。这是因为射弹受到来自包裹射弹头部极小部分流体的持续作用，同时入水角度也会影响射弹受力的方向，最终使射弹绕头部小幅度摆动，导致法向力系数出现波动现象。长径比相同时，射弹初始越大，射弹受水的反作用力越大，轴向力系数和法向力系数的波动越剧烈，这是因为射弹长径比越大，射弹重心越远离射弹头部，射弹受扰动后越难以恢复，使轴向力系数和法向力系数波动越剧烈。

3.3 射弹应力响应分析

不同长径比射弹在不同初始条件下最大应力随时间的变化见图11。

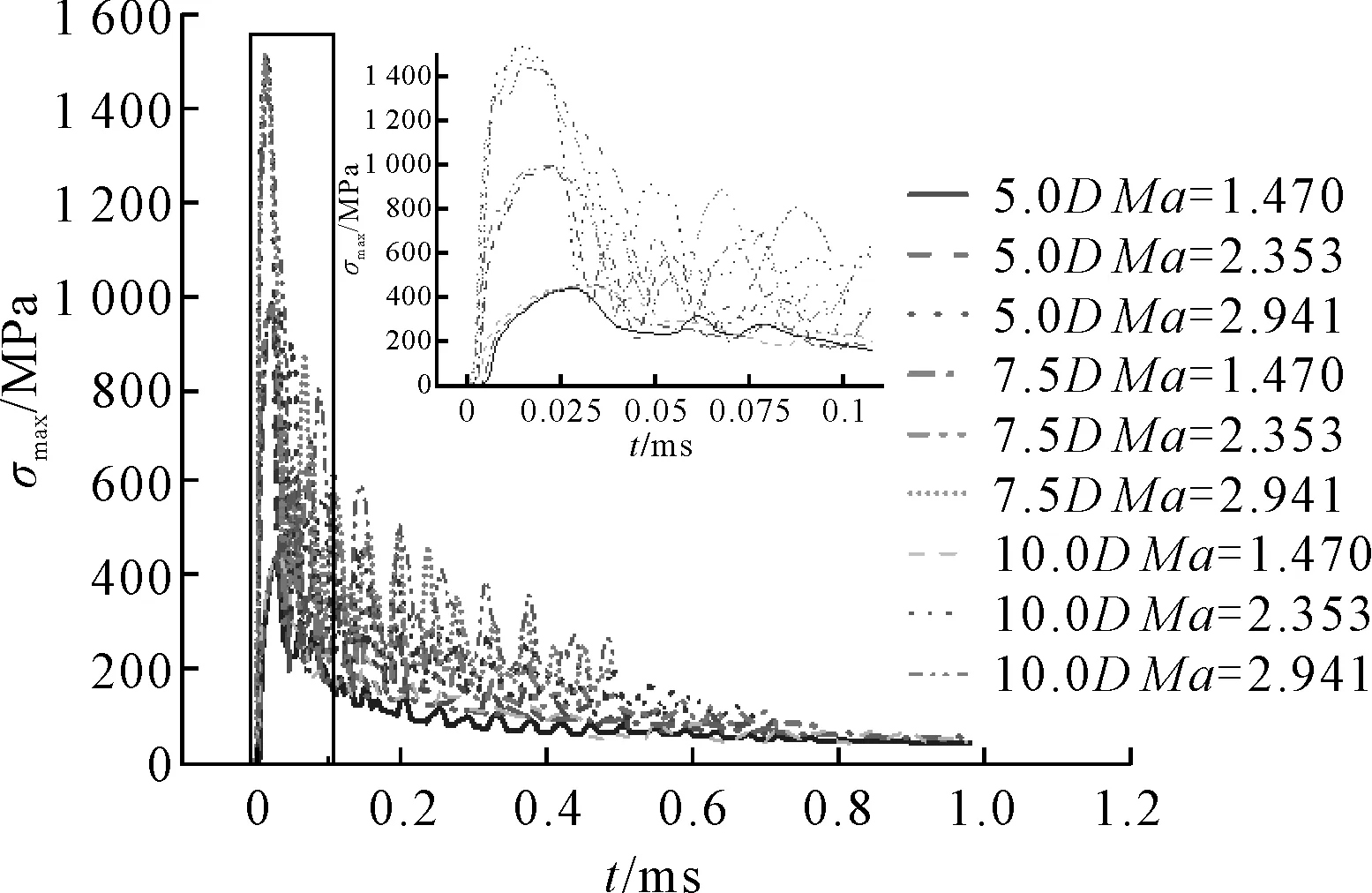
图11 最大应力随时间的变化

为最大应力。由图11可知，最大应力峰值出现在射弹抨击自由液面瞬间，最高达1 500 MPa，之后又迅速降低，且长径比相同时，射弹最大应力峰值随初始增加而增加。而射弹最大应力随射弹长径比增加，变化不明显，说明长径比对射弹最大应力影响较小。

不同长径比射弹在不同初始条件下抨击自由液面瞬间的应力见图12～14。共有3个时刻，分别为射弹下平面下沿接触水面时、下平面中部接触水面时、下平面上沿接触水面时。

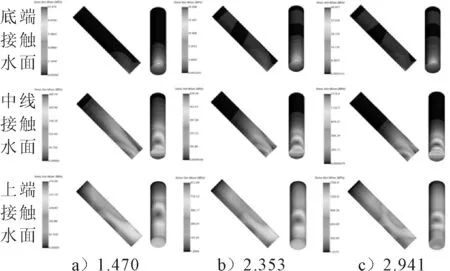
图12 5D射弹应力云图

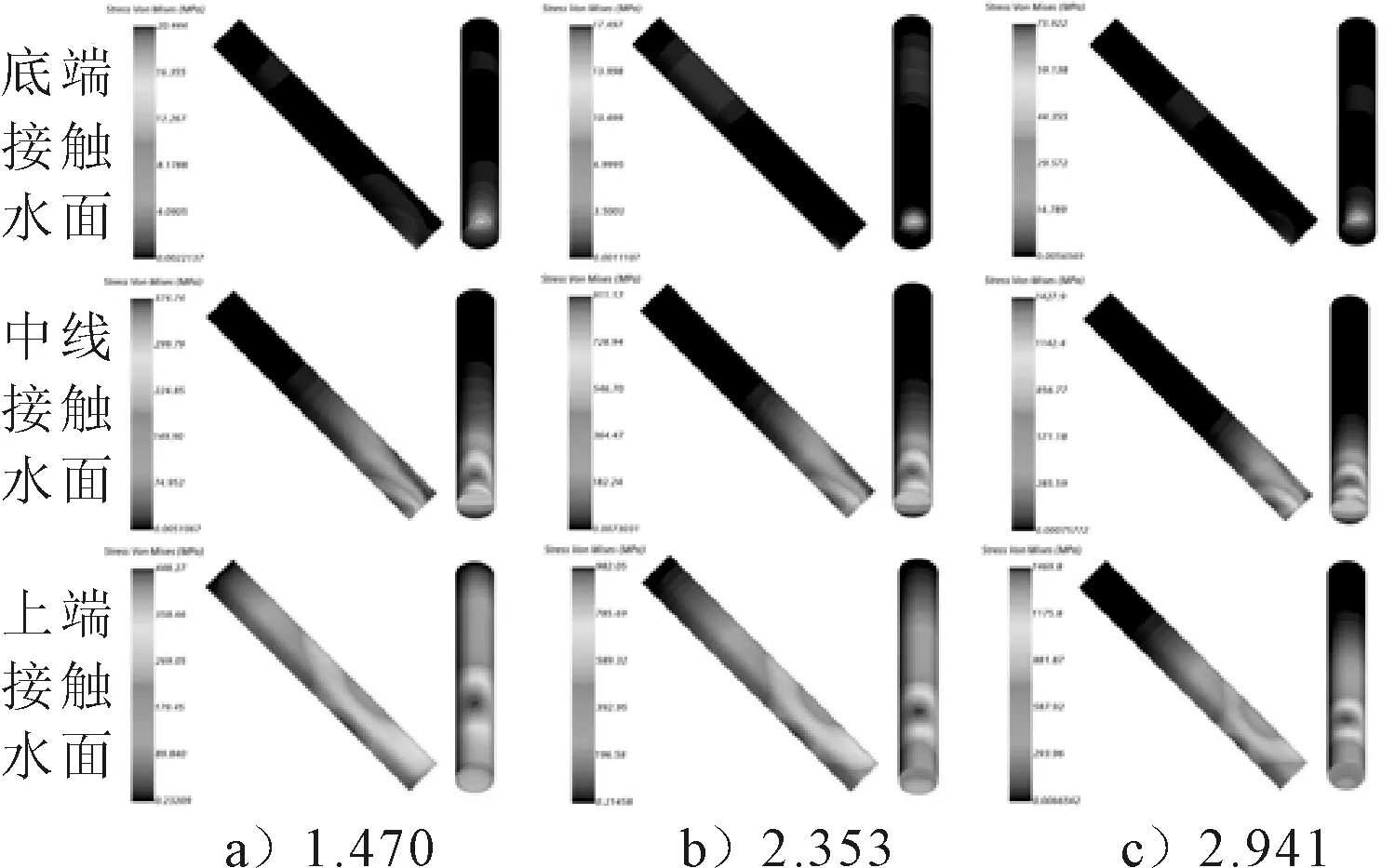
图13 7.5D射弹应力云图

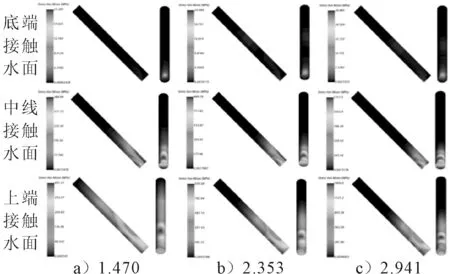
图14 10D射弹应力云图

由图12～14可知，入水过程中射弹最大应力区域基本位于射弹下端附近区域，当射弹在射弹下平面下沿触水时，触水点应力迅速增大，且呈贝壳状对称分布；当射弹底面中轴线触水时，最大应力位置上移；当射弹底面上端点触水时，射弹最大应力位置继续上移。因射弹受到水的冲击作用后，射弹出现动态稳定性问题，随时间推移应力波在弹体中向后传播。

3.4 空泡形态演化规律分析

不同长径比射弹在不同初始条件下入水0.4 ms后的水相云图见图15。

图15 水相云图

从图15可以看出，在射弹超音速入水时，流体会贴附在射弹下部，伴随射弹运动，即附连水现象。因为流体具有黏性，流体的伴随运动会使射弹下部流体贴合在射弹壁面，从而影响空泡外形。7.5射弹45°入水时最为明显。原因为75射弹长度适中，在入水过程中尾部不断拍击附连水，极大地影响附连水形状，5与10射弹因长度原因，尾部不能持续拍击附连水，所以不能影响附连水形状。

量纲一的量空泡直径随时间的变化见图16。

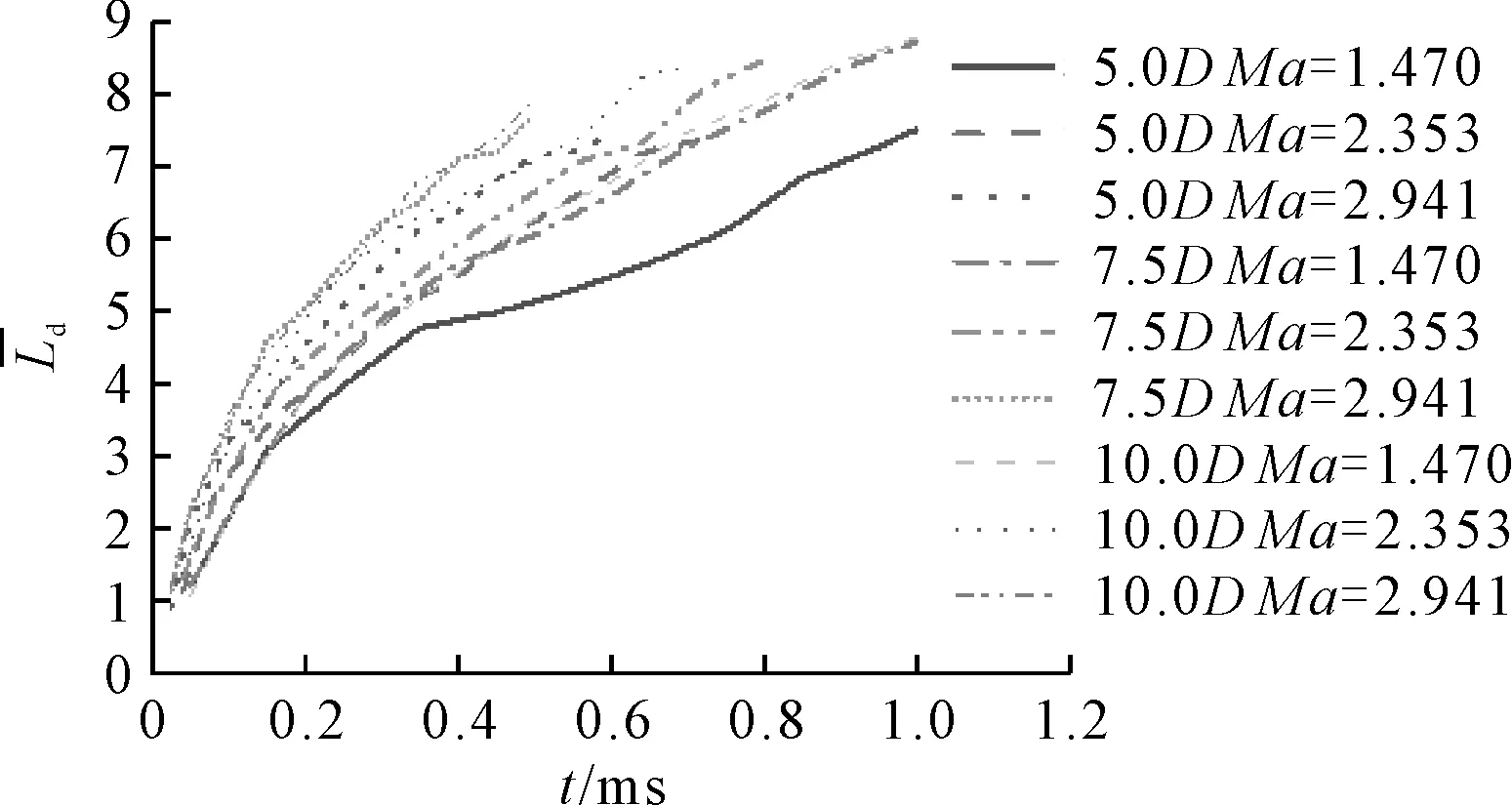
图16 无量纲空泡直径随时间的变化

由图16可见，入水过程中空泡有较为明显的生成阶段，初始较大时，长径比对量纲-的量空泡直径的影响更大。

量纲一的量空泡长度随时间的变化见图17。

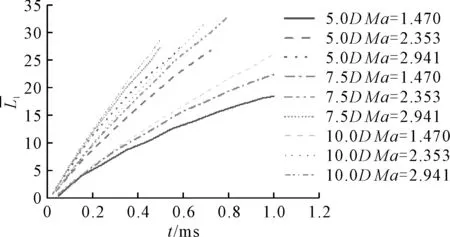
图17 无量纲空泡长度随时间的变化

由图17可见，射弹长径比对量纲一的量空泡长度变化影响更大，因为当射弹长径比较大时，射弹速度衰减更慢，所以相同时间下大长径比射弹的量纲-的量空泡长度更长。

3.5 流场最大压强变化规律分析

流场的最大压强随时间的变化见图18，为最大压强。

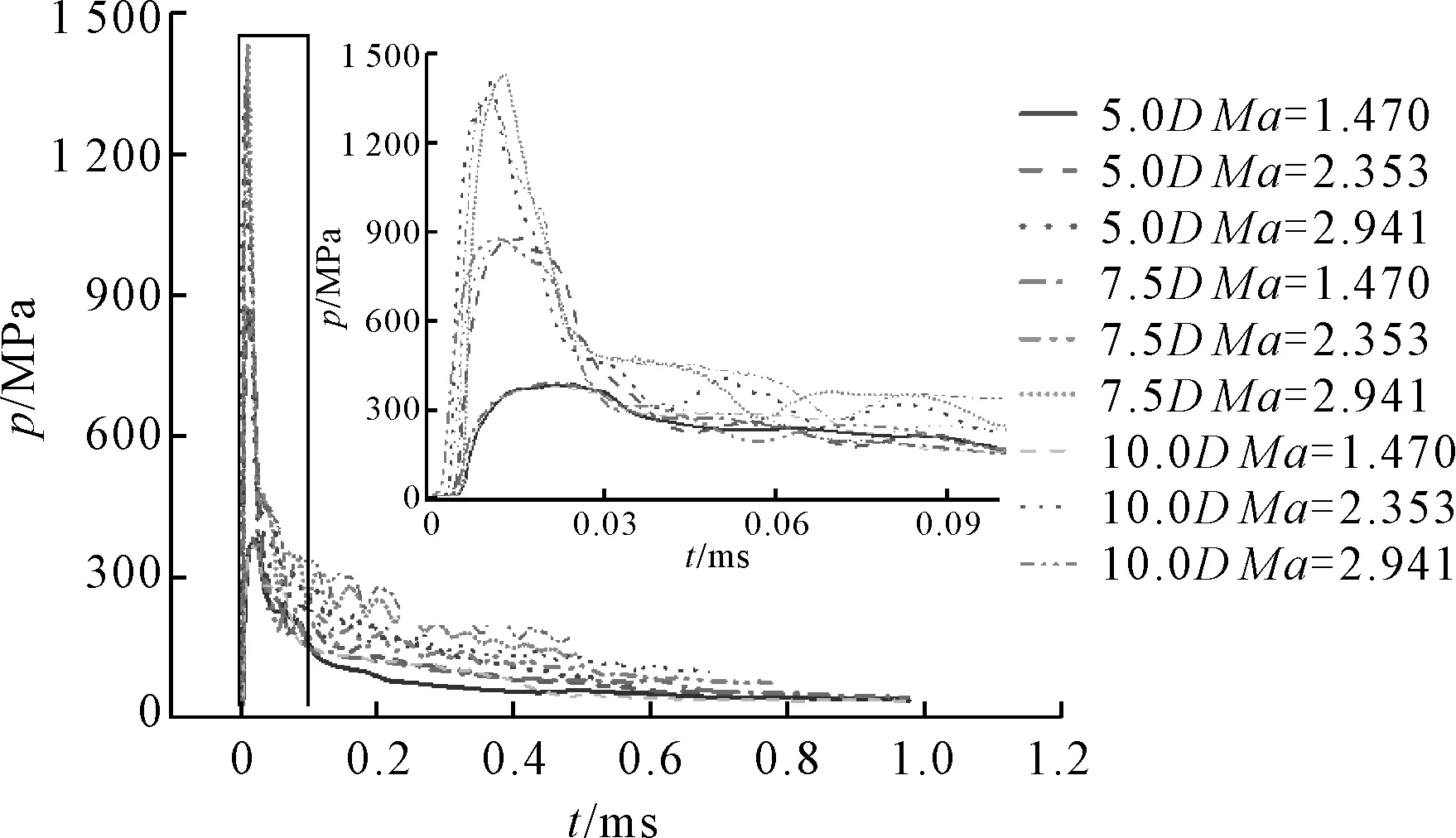
图18 流场最大压强随时间的变化

由图18可见,流场最大压强峰值出现在射弹抨击自由液面瞬间，入水后流场最大压强急剧下降，入水时间越长，流场最大压强越低，衰减速率越慢。射弹初始入水越大，流场最大压强峰值越大，射弹长径比对流场最大压强影响较小。

选取5射弹算例进行分析，不同时刻，不同初始条件下的流场压强见图19。射弹抨击自由液面瞬间，射弹前方较远处流场压强基本无变化，说明此时这些区域流场受到的扰动较小。射弹在入水初期，头部撞击液体产生的压力波近似呈心形向整个流场传播，靠近撞击点区域的压强较大，远离撞击点区域的压强较小。初始为2941时，因模型尺寸小，压力波在撞击水缸壁面后与包裹射弹头部的压力波相互迭加，使压力场不再规则。

图19 流场压强云图

4 结论

1)射弹抨击自由液面瞬间，轴向力系数和法向力系数达到峰值，相同入水条件下，长径比越大，轴向力系数和法向力系数最大值越大。射弹入水后，轴向力系数和法向力系数迅速下降，且不同长径比射弹轴向力和法向力变化趋势相似。

2)最大应力峰值出现在射弹抨击自由液面瞬间，随后迅速下降，且长径比相同时，射弹最大应力峰值随初始入水增加而增加，长径比对射弹最大应力影响较小。弹体拍击流体导致射弹不断绕头部小幅度震荡，弹体应力最大值产生在射弹近水面而非头部，影响射弹运动稳定性。

3)射弹抨击自由液面形成的压力波呈心形变化，先扩张后收缩。当射弹初始入水马赫数较高时，受扰动流体在撞击壁面后与包裹射弹头部的流体相互作用，使压力场不再规则。