基于Seq2Seq的机组组合优化决策方法研究
叶 迪
(国网福建省电力有限公司福州供电公司)
0 引言
机组组合(Unit Commitment,UC)问题是日前电力市场决策和发电计划编制的重要理论基础之一[1]。目前对机组组合问题的研究以模型构建和算法研究为主[2]。在当今能源变革日新月异的背景下,机组组合面临的理论挑战层出不穷,这种传统的基于物理模型驱动的决策方法已经难以适应电力系统快速发展的实际需求。
从工程实际而言,调度方法一旦用于实际,往往会积累大量结构化的历史数据,从长期来看,机组组合决策也具有一定的重复性,往年积累的历史决策方案对于未来的机组组合决策也具有指导意义,而且实际运行决策数据往往是模型计算和人工修正结合的产物,因此,在理论上可以说是考虑了当时所面对的各种影响因素和限制条件[3]。同时,深度学习技术已经在解决诸如输电线路故障判断[4]等电力系统实际问题中取得良好效果。因此,国内团队提出一种基于数据驱动的机组组合决策方法,不研究机组组合的内在机理,而是通过长短时记忆网络(Long Short-Term Memory,LSTM),利用海量历史决策数据训练,直接构建已知输入量和决策结果间的映射关系[5]。
基于数据驱动的机组组合决策方法是以深度学习模型和训练样本为核心,通过深度学习模型学习训练样本之间的映射关系得到映射模型,并以此进行机组组合决策。可供使用的深度学习模型有循环神经网络(Recurrent Neural Networks,RNN)、LSTM[6]和门限循环神经网络[7](Gated Recurrent Unit,GRU)等。随着电力系统的发展,历史训练样本已经由类型单一、机组数目不变转变为类型多样且机组数目增加,因此现有的基于数据驱动的决策方法存在以下几个缺点:
1)这种研究思路必须使用聚类算法,无法单独处理含多种类型样本的训练集。
2)对每一次训练而言,GRU模型的结构都不会改变,这就要求所有的样本数据都具有相同的结构。
作为对现有基于数据模型驱动的机组组合决策方法的有效补充,本文方法主要有以下创新。
本文方法不需要再对历史数据进行聚类处理,而是基于Seq2Seq模型,对于不同类别的训练样本,仅需要较少历史调度数据,即可构建日负荷和机组组合方案之间的映射关系,能够直接处理样本未聚类的SCUC问题,具有广泛适用性。
基于标准算例的一系列仿真结果验证了本文方法的正确性和有效性。
1 基于Seq2Seq模型的数据驱动机组组合决策框架
基于数据驱动的机组组合决策的最大特点是在长期使用过程中通过数据积累实现自我进化,以适应电力系统的发展。而在较长时间周期内,机组组合决策每一个训练样本的结构有可能并不相同,其样本构成的是一种输出序列维度可变的弹性样本矩阵集合。如果直接将传统的GRU模型用于机组组合映射关系的训练,在面对不断变化的样本结构时,其适用性将很难保证,针对该问题,本文提出一种应对机组维度变化的数据驱动机组组合决策框架,决策框架如图1所示。

图1 基于Seq2Seq的数据驱动决策方法框架
对于机组维度变化的机组组合问题,本文方法首先使用机组数目转换模型将样本转换为维度相等且能够供Seq2Seq模型训练的训练样本。其次对此类样本聚集的训练集进行样本编码处理,将机组组合矩阵转换为包含矩阵所有机组启停信息的样本编码行向量。在决策过程中,Seq2Seq模型对输入、输出序列进行分步录入操作,从而使每一个神经网络的神经元数量可变,且可以根据输入输出序列的长度自适应调整,因此训练集内样本的多少不会影响模型的决策精度。而且,随着不同类型历史数据的积累,可供模型训练的训练样本个数不断增加,因此模型求解不同类别历史样本数据的兼容性会随着数据的积累而不断提升。但是,随着训练集容量的增加,Seq2Seq模型的训练次数需要进行相应调整,不然容易出现过拟合或欠拟合问题。
2 基于Seq2Seq的机组组合深度学习模型及训练算法
对于机组组合历史调度数据这类与时序紧密关联的训练样本,节点相互独立的深度学习模型无法适用,而RNN这类时序模型具有处理时序相关数据的能力。但是,面对序列较长的样本时,RNN模型会出现梯度消失现象。作为RNN的一种改进型,LSTM实现了模型对重要信息的记忆,有效解决了RNN训练过程中可能出现的梯度消失的问题,但是其模型过于复杂,在处理高维度的训练样本时,不仅需要大量的计算资源,而且容易出现过拟合现象。针对该问题,Kyunghyun Cho等人在LSTM的基础上将输入门与遗忘门合并,并简化记忆单元,提出一种新的网络模型,即GRU,有效降低了模型的复杂度。由上文分析可知,单独使用GRU模型仅能处理输入、输出序列维度均固定的样本,无法学习训练集中机组数目发生变化的训练样本。因此,以GRU模型为基础,本文将构建一个包含Encoder-Decoder框架的基于Seq2Seq模型的机组组合深度学习模型。该框架的示意图,如图2所示。

图2 Encoder-Decoder架构
由图3可知,与传统循环神经网络模型用单个神经元读取所有输入量不同,Encoder是将输入序列按照时间步骤分步读入,然后再输出整个序列的中间状态C。由于循环神经网络可以记录每一个训练步骤的过程信息,因此理论上中间状态C能够计及整个输入序列的信息。而在Decoder中,另一个循环神经网络执行与Encoder相反的操作,把得到的中间状态C分步解码,形成最终的输出序列。由此可见,Seq2Seq技术巧妙利用循环神经网络的时序记忆特性,采用两个神经网络构成的复合结构对输入、输出序列进行分步录入操作,从而使每一个神经网络的神经元数量可变,且可以根据输入输出序列的长度自适应调整,成功实现了对维度可变的样本序列的处理。
3 基于Seq2Seq的机组组合深度学习模型构建
针对机组组合历史样本数据的时序特征,本文构建的Seq2Seq模型中,Encoder模型的第t时间步的输入输出关系如式(1)~式(5)所示:
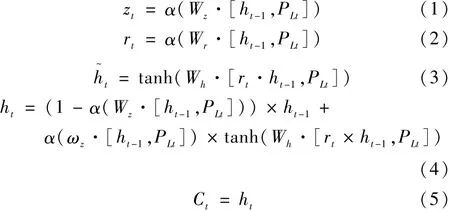
式中,PLt为考虑时序特性的输入参数;zt和rt为更新门和重置门;为GRU的待定输出值;ht为GRU的隐藏状态;ht-1为前一时刻GRU的隐藏状态;Wr为输入数据和zt之间的权重系数;Wz为输入数据和rt之间的权重系数;Wh为输入数据。α为神经网络中激活函数sigmoid。
根据式(1)~式(5),最后一个时刻GRU神经元的输出状态CT即为该Encoder的输入中间状态Ci。
以GRU为神经元,基于Seq2Seq技术构建Decoder模型如图5所示。其中Decoder模型的第m时间步的输入输出关系如下所示:

式中,zm为第m个神经元的输出状态向量;xm为第m个神经元的输入数据;Hm为第m个神经元的输出数据;其余参数符号意义与Encoder相同。
4 算例分析
本文算例的日负荷样本以湖南电网日负荷特性曲线为基础进行构造,SCUC模型建模基于IEEE118节点系统,调度方案由CPLEX 12.5计算得到。基于Seq2Seq以及GRU的机组组合数据驱动模型均在Tensorflow 1.6.0平台上完成训练和测试。相关仿真计算均在英特尔酷睿i5-4460处理器/3.20GHz,8G内存计算机上实现。
为了证明本文方法使用数据驱动和物理模型驱动相结合这一思路的有效性,使用本文方法与基于物理模型算法对第一类测试样本进行决策,通过比对二者的决策时间来验证本文方法的有效性。本文方法中数据驱动部分决策机组组合方案U,物理驱动模型求解经济调度过程,具体仿真结果如表1所示。

表1 本文方法和物理模型驱动方法对比
由表1可知,本文方法的总费用与基于物理模型驱动的决策模型完全相同,本文方法能够节省2/3左右的决策时间。由此可知,本文方法能够在保证决策精度的同时,具有更高的决策效率。为了进一步验证数据驱动模型求解机组组合方案U的决策精度高低对整个决策模型所造成的影响,将表1中第三类测试样本在1000次、1500次和2000次训练映射模型1所得到的机组组合方案代入本文方法,并比对最终决策结果,具体仿真结果如表2所示。

表2 不同决策精度的机组组合方案对最终结果影响
由表2可知,较低的训练次数会导致映射模型的决策精度降低,较低的决策精度最终会反馈在总费用上,决策精度越低,调度的总费用则越高。因此,上述仿真证明了求解机组组合方案U是本文方法的关键环节。
5 结束语
本文提出一种基于Seq2Seq模型的数据驱动机组组合智能决策方法。通过GRU-S2S模型学习日负荷与调度方案之间的映射关系,构建映射模型,并使用其进行机组组合决策,求解得到机组调度方案。本文得出的具体结论如下:
1)相较于基于物理模型驱动的决策模型,本文提出模型在具备相同经济效益前提下具有更短的决策时间,决策效率更高。
2)在处理SCUC问题时,本文模型证明较高的训练次数可以有效提高决策精度,并进一步提高本文方法的经济性。

