基于GIS 的城市暴雨洪涝模拟分析——以郑州市石佛镇“7·20”特大暴雨为例

钟源，孟庆祥

（武汉大学遥感信息工程学院，湖北武汉 430072）

0 引言

“7·20”郑州特大暴雨是千年一遇的灾害，它给市民的生命和财产造成了巨大的损失。据报道，郑州7 月20 日16-17 时（1 h）降雨量达201.9 mm，相当于上百个西湖的蓄水量在1 h 内倾入郑州，打破了“758 特大暴雨”1 h 降雨量198.5 mm 的纪录，成为我国陆地小时降雨量极值。

为解决城市洪涝问题，一些发达国家已经进行城市雨洪模型的研究，其中适用性较高的有，用于模拟单场降雨或长期水量水质变化的动态降雨径流模型SWMM（Storm Water Management Model）［1］，常用于城市排水和内涝分析的Infoworks ICM［2］，基于流域尺度的长时段分布式水文模型SWAT（Soil and Water Assessment Tool）［3］等。在我国岑国平等人提出了首个完整的城市雨水径流模型（SSCM）［4］。国内学者还提出了城市雨水径流模型（CSYJM）［5］、平原城市水文过程模拟模型［6］，城市分布式水文模型（SSFM）［7］等。此外，还有不少研究是在国外的SWMM、Infoworks ICM 等模型的基础上，结合当地资料和某一特定主题进行改善而提出的，但存在功能指向性强、可推广性较差的问题［8，9］。在城市雨洪模型可操作性和可视化方面，国内涌现了一些与GIS 结合构建城市雨洪模型的研究，如黄国如等人基于GIS（Geographic Information System）对SWMM 进行二次开发［10］、周红等人基于GIS 和SWMM 对厦门市马銮湾片区进行模拟和效益评价［11］、刘为提出基于GIS 和SWMM 将溢出洪量进行有源淹没的方法［12］等，但是该类研究需要借助GIS 来生产和处理水文模型所需相关的地理数据。综上所述，对于城市暴雨研究，国内外学者针对部分水文模型或者暴雨洪涝的某个阶段的分析已经比较成熟，但是针对极端暴雨洪涝（城市）还缺乏全流程系统性的模型推演及风险评估方法。

1 数据来源

以郑州市石佛镇为研究区域，模拟推演“7·20”事件中，暴雨洪涝的时空发展过程。石佛镇位于郑州市郊西北部，管辖陈庄、大里等17个行政村。其地势东北低，西南高，东北主要为开阔的农用地，而城市地区主要集中在中部及以下。图1 为石佛镇卫星影像，图2（a）为10 m 分辨率的用地类型，图2（b）为剔除建筑物后的DSM，图2（c）为建筑物和交通数据。

图1 石佛镇卫星影像Fig.1 Satellite image of Shifo town

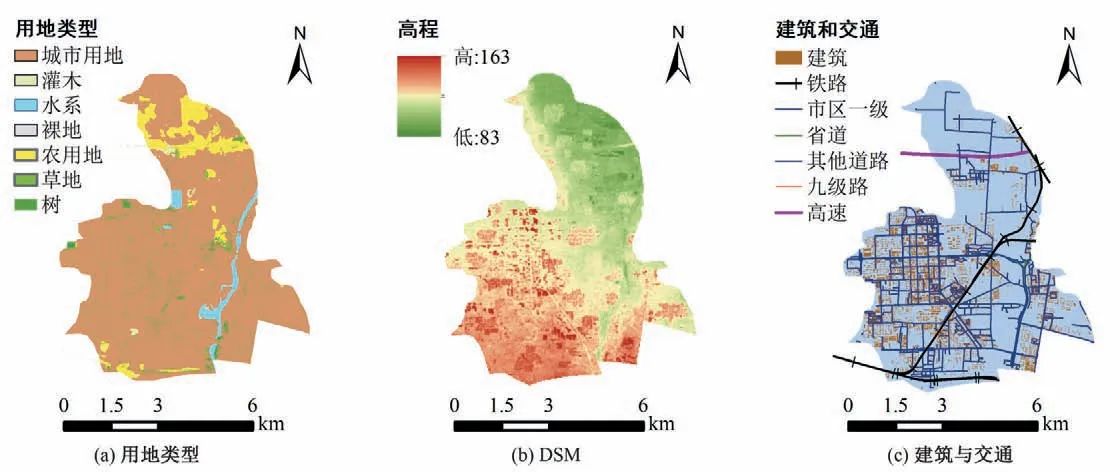
图2 试验区域数据Fig.2 Data of study area

为验证模型正确性和有效性，本文使用当地时间7 月21 日早6∶31 时的高分三号卫星影像（如图3 所示）进行模型计算结果与实际情况的对比验证。

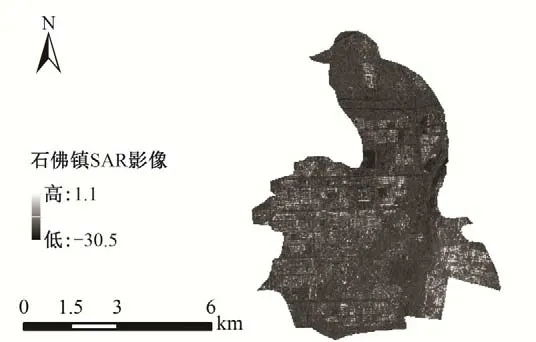
图3 试验区SAR卫星影像Fig.3 SAR image of Study Area

2 城市暴雨洪涝模型

2.1 建模流程

本文构建用于推演极端暴雨灾害的城市暴雨洪涝模型，其建模流程如图4所示。首先由实测降雨数据得到较为合理的芝加哥雨型参数，再对剔除建筑物以后的DSM 进行流域分割，然后根据降雨量和径流模型计算各个子流域的洪水量，再将子流域的高程信息输入淹没模型，计算得到各个子流域的时序淹没深度，最后对建筑物和交通的受灾情况进行分析。

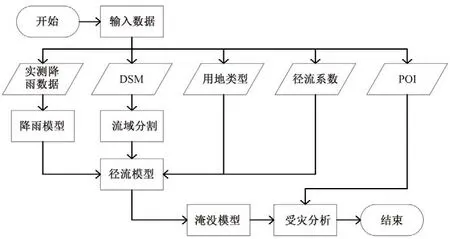
图4 建模流程图Fig.4 Modeling flow chart

2.2 流域分割

虽然极端暴雨通常会导致整个区域都处于被淹没的状态，但是洪水有一定的作用范围，不会全部汇入整个区域的最低地区。因此，本文首先对区域进行流域分割，再对子流域进行径流—淹没分析。流域分割的流程如图5所示。其中流向计算采用D8 算法［13］，即根据中心栅格与邻域的最大高程落差来确定该栅格的水流方向。在河网计算中，需要根据像元大小确定流量栅格所统计的汇水面积，超过一定阈值就认为该栅格为河网单元［14］。最后，由于该过程会得到一些极小的流域，可以通过设定阈值，将面积小于阈值的极小流域合并到相邻流域中。

图5 流域分割流程Fig.5 Watershed segmentation process

2.3 降雨模型

“7·20”暴雨有两次峰值，但是第二次峰值降雨强度远高于第一次，所以本文采用单峰雨型——芝加哥雨型来模拟［15］，由暴雨强度公式推求的合成降雨过程线公式如下：

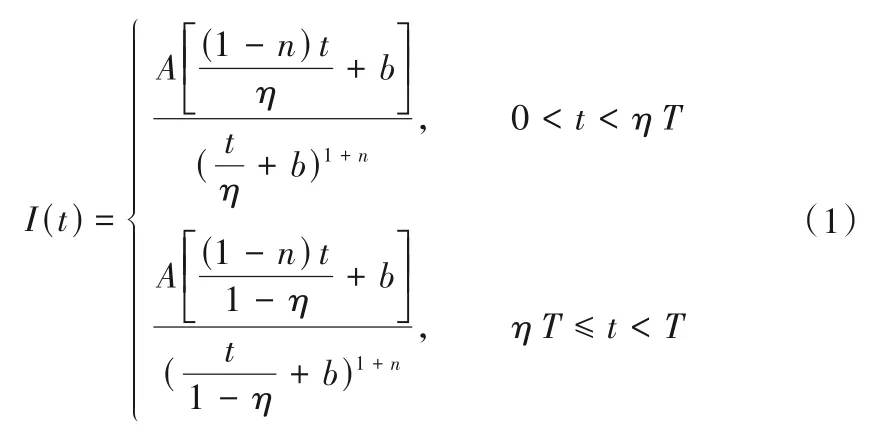
式中：A，b，C，n是与暴雨特征有关的参数，η为雨峰系数，I(t)为瞬时降雨强度。

2.4 径流模型

降水的一部分不产生径流，而是在降雨初期的植被截流、填洼、下渗、蒸发等过程中损失。径流系数是任意时段内径流深度与同时段的降水深度之比，城市地区可以采用径流系数法计算径流量，由于每个子流域包含不同类型的下垫面，因此采用面积加权平均的方法计算每个区域的平均径流系数。使用式（2）计算径流量，其中Q为径流量，P为降水量，Si和φi分别为用地类型为i的地块的面积和对应的径流系数。

不同下垫面对应的径流系数如表1所示。

表1 径流系数对应表Tab.1 Corresponding table of runoff coefficient

径流量还有一部分损失在排水系统中。在缺少排水数据的情况下，可以根据当地设计排水标准，使用经验公式简化排水计算，使其能在保有一定精度的情况下参与整体模型计算。在逐小时计算的推演过程中，如果出现径流量小于排水量的情况，在后续累计水量计算中，需要扣除排水能力溢出部分。

2.5 淹没模型

获取到洪水水量后，进行淹没计算。淹没模型是基于2.2流域分割结果，各子流域内洪水从区域最低处开始淹没。该模型输入为洪水量（mm）、淹没深度增加的步长（m）、由区域的DSM 进行空间统计得到的高程—栅格集合（即区域内每种高程值对应的栅格数量组成的数组）。模型输出为该区域的淹没深度（m）。具体流程如图6所示。

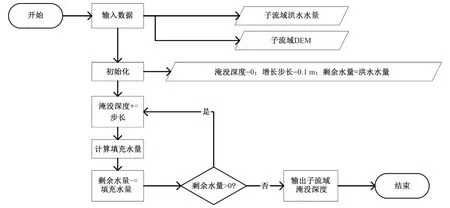
图6 淹没模型流程图Fig.6 Flow chart of flooding

3 实验结果及分析

3.1 流域分割

在河网计算中，设定实际汇水面积超过0.025 km2的流量栅格为河网。在合并较小流域的过程中，将流域面积小于0.025 km2的子流域合并到相邻流域中。石佛镇流域分割的结果如图7所示。

图7 石佛镇流域分割结果Fig.7 Watershed segmentation result of Shifo town

3.2 降雨模型计算

由于“7·20”事件的特殊性（当日降雨量远远超过国家界定的特大暴雨界线，即24 小时降雨量大于等于250 mm，而当天降雨量高达600 mm），因此如果采用当地一般性降雨参数配置公式，其模拟结果与现实情况偏差较大。通过多次试验，得到式（1）的如下参数配置A=67.775 4；b=75.042 2；n=0.694 1；η=0.747 2。

合成降雨过程线如图8（a）所示，由模型积分反推得到的累计降雨量曲线如图8（b）所示。在参数校正过程中，以降雨过程线曲线趋势、雨峰位置、雨峰强度以及24 h 累计降雨量的实际值为参考标准，最终确定参数配置。

3.3 径流—淹没模型计算

对石佛镇各子流域应用径流—淹没模型得到的各子流域的积水深度随时间变化图如图9所示，其中，水深是以该子流域的高程最低点为参考值的。

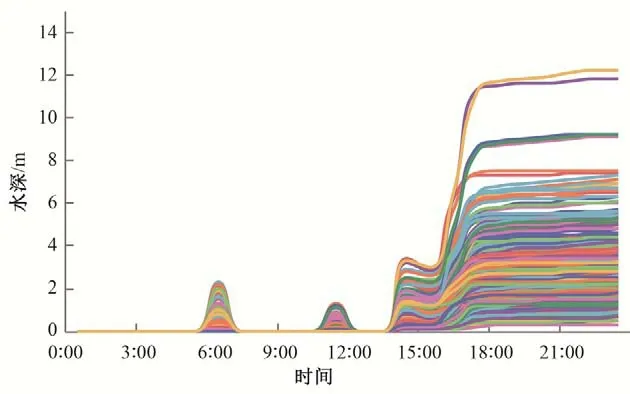
图9 各子流域积水深度变化图Fig.9 Variation diagram of ponding depth in each sub watershed

石佛镇“7·20”总体积水淹没情况如图10所示。

图10 石佛镇“7·20”积水淹没情况Fig.10 “7·20”ponding inundation in Shifo town

由于7 月20 日当天的实测数据无法获取，因此本文使用当地时间7 月21 日早6 点31 分的高分三号卫星影像提取的水体数据（如图11 所示）与模型输出的23∶00 时刻淹没情况进行比较。

图11 中可以看出，实际淹没情况在东北部较深，中部及南部较浅，与模型计算结果水深分布基本一致。试验结果对比如表2所示。

表2 模型计算结果与卫星影像数据对比表Tab.2 Comparison between model results and satellite image data

图11 7.21卫星影像提取的水体Fig.11 Water area extracted from 7.21 satellite image

从上述与实际数据的对比中可以看出，模型计算结果在地理分布和水深程度上都是符合实际情况的。

3.4 试验结果分析

从模型计算结果看，在6 点和11 点分别有一次降雨小高峰，但是积水范围小、深度浅，影响不大；从14 点开始一直持续到晚上，累计降下约450 mm 的水量，从图中可以直观看出淹没范围、淹没深度的增长情况；下午16 时到17时，一小时内降雨量达201.9 mm，在图中可以明显观察到积水范围几乎完全覆盖区域，且严重积水区（图中深色部分）明显增多；由于暴雨一直持续到晚上（17 时到23 时累计降雨约170 mm），因此积水的面积、深度居高不下。由于石佛镇地势西南高、东北低，从图中能看到积水深度较深的地方主要集中在东北部人烟较为稀少的地方。

将积水淹没的计算结果与石佛镇的建筑物、交通数据结合分析，可以统计出24 h内，处于不同积水深度影响下的建筑物、交通的占比情况，如图12、13所示。

图12 不同积水深度影响的建筑物占比随时间变化Fig.12 The proportion of buildings affected by different ponding depth changes with time

图中呈现了降雨强度随时间变化的曲线（绿线），其中统计建筑物总数为6 558栋，交通总里程为264.1 km。从面积堆叠图可以直观看到，建筑物与道路受积水影响的趋势以及变化程度是一致或相近的。而从石佛镇的建筑、道路分布图能看出，建筑和交通在位置上基本是耦合的，这表明模型的计算结果具有真实性。处于1.5 m 水深影响以下（图中红色面积及以下部分）的建筑/交通在15 时之前都占绝大部分（90%）。而15 时到17 时的两个小时内，由于降雨强度急剧上升，安全水深区域占比急速下降至20%。在24 h内，处于3 m 以下水深的始终在75%以上。

图13 不同积水深度影响的交通占比随时间变化Fig.13 The traffic proportion affected by different ponding depth changes with time

4 总结

本文构建了基于GIS 的城市暴雨洪涝模型，系统地推演了极端暴雨洪涝灾害，辅之以灾害发生过程的时空可视化手段，对“7·20”特大暴雨灾害进行建模、推演与模拟分析。

针对郑州石佛镇试验区，本文耦合了流域分割、降雨建模、径流建模、淹没建模及受灾分析多个模型，系统性地推演了试验区暴雨洪涝的全过程。在试验验证中，特别是利用SAR 卫星数据和本文实验结果进行多方面对比，结果表明本文所提模型的正确性和有效性。

本文所提模型可以对极端暴雨引发灾害全生命周期进行计算，用于推演极端暴雨洪涝灾害全过程，为模型推演及灾害分析提供了系统性方法，具有一定的适应性。城市暴雨洪涝模型中涉及多模型耦合，机理复杂，只有全面提升模型耦合能力和系统评估分析能力，才能做到科学防灾治灾。