基于改进组合赋权法的区域水资源承载力评价

李治军，王涛

（1.黑龙江大学水利电力学院，黑龙江哈尔滨 150080；2.黑龙江大学寒区地下水研究所，黑龙江哈尔滨 150080）

0 引言

水资源是人类生存和社会发展的必要资源，随着社会的进步与发展各行业对水资源的需求量不断增加，如何解决供需不足的矛盾已经成为我国经济社会可持续发展的重要问题［1］。水资源承载力由我国学者于20 世纪80 年代末所提出，水资源承载力是区域生态环境建设和确定社会经济健康发展方向的基础，是对水资源在时间和空间上的一个度量尺度［2］。研究水资源承载力不仅有利于弄清生态环境、社会经济与水资源的空间关系，更是在水资源安全战略研究和可持续协调发展中起到了不可或缺的作用［2］。

现如今水资源承载力评价计算权重的方法大致可以分为两类，一类是有相关领域专家判定指标间的相对重要程度的赋权方法，如：层次分析法（Analytic Hierachy Process，AHP），该种方法主观性强，人为影响要素较大，不适用于具有不确定性的定量评价中［3］。在实际的复杂系统中，系统诸要素间是相互作用的，不同层次间的元素也是相互影响的，采用AHP 方法求解必然存在不准确和不科学之处。另外一类是依据各指标样本数据提供的信息进行的赋权方法，如熵权法（Entropy Weight Method，EWM）该方法杜绝了主观要素的影响，但是难以表达出指标间相互影响的关系［4］。而且传统熵权法具有一定缺陷，每个熵间细微的变化在一定情况下可能会导致各指标熵权间的成倍变化［5］。

针对以上问题，本文采用网络层次分析法（Analytic Network Process，ANP）与改进的熵权法共同计算组合权重，Saaty 提出的ANP 法能够解决层次分析法（AHP）模型难以准确计算具有依赖性、反馈性的决策问题，揭示指标集内外部间存在的相互作用关系，适用于无法精确建模为层次结构的经济社会等问题［6］。通过改良后的熵权法模型能够解决由于每个熵间的细微变化而导致成倍增长的问题。计算出的权重进行组合赋权更好的提高了权重的稳健性。本文所提供的方法为日后水资源承载力评价研究提供新思路和参考。

1 研究方法

1.1 指标识别及构建评价体系

水资源承载力评价模型的建立是一个系统的工作，指标的确定需要考虑多方要素的影响，本文指标选取按照SSHIO 原则（系统性Systematicness、特定性Specificity、层次性Hierarchy、独立性Independence、可操作性Operability）并通过阅读大量文献对已有研究结果进行总结并进行专家咨询并结合研究区域实际情况，基于WEE（水资源Water Resource－经济Economics－生态Ecology）建立评价体系［7］。本文建立以水资源、经济、生态为一级评价指标，以人均水资源量、产水模数、降雨量等16个指标作为二级评价指标建立芜湖市水资源承载力评价体系，见图1。

1.2 DEMATEL确定影响关系

决策实验室法（Decision Making Trial and Evaluation Laboratory，DEMATEL）是Bottelle 研究所于1971 年提出的一种决策方法，能够有效地确认准则或各元素之间的因果关系及相互影响程度，通过建立指标间因果关系来研究和解决较为复杂的系统问题［8］。通过DEMATEL确定影响关系具体步骤如下：

（1）确定指标并判断关系：分析评价体系中选取的各指标元素，通过调查问卷的方式判断各元素直接的相互关系，各指标元素记为Xi（i=1，2，3，…，16）。

（2）确定系统要素间直接影响关系，构建直接影响关系矩阵D，直接影响关系矩阵通过专家对各指标间影响大小判断形成。

式中：n为指标个数；a21为指标a2对指标a1的影响程度且对角线均为0。

（3）影响关系矩阵标准化处理。

（4）构建综合影响矩阵。

1.3 利用ANP确定指标权重

ANP 是层次分析法AHP 的基础上进一步改造、完善的，它考虑了同一等级各指标要素间的相互关系，是一种更加科学准确的决策方法［9］。使用ANP确定指标权重计算过程如下。

与治疗前相比，观察组和对照组治疗后1、2个月的骨保护素水平均显著升高(P<0.05)；其中观察组治疗后2个月骨保护水平显著高于治疗后1个月(P<0.05)。组间相比，治疗前和治疗后1个月，观察组牙周组织骨保护素水平与对照组相比均无统计学差异(t=1.765, t=1.766；P>0.05)；治疗后2个月，观察组牙周骨保护素水平显著高于对照组(t=5.925，P<0.05)(表1)。

（1）根据DEMATEL 求得综合影响矩阵建立水资源承载力评价的ANP 的网络结构，见图2。图2 中双箭头表示两簇中的节点指标互相影响，环向箭头表示该簇内节点指标相互影响［9］。

图2 水资源承载力评价网络结构图Fig.2 Water resources carrying capacity evaluation network structure diagram

（2）根据1～9 评估尺度表［10］，见表1。对每个指标重要性程度进行判别构建判断矩阵，对判断矩阵进行归一化处理后进行一致性检验，从判断矩阵中求解最大特征值、特征向量，通过得到的特征向量构建未赋权的超矩阵。

表1 1～9尺度表Tab.1 1～9 scale

（3）对w矩阵进行归一化处理，在对矩阵赋权得到赋权超矩阵。

1.4 利用改进熵权法确定指标权重

1.4.1 熵权法的基本原理

熵权法是一种依靠评价指标体系中各指标的相关数据多少来进行确定指标权重的赋权方法，熵权法是一种客观赋权法［12］。熵权法是管理科学中经常使用的技术手段，它利用数据本身的无序化和不均匀程度来体现指标中含有信息量多少，进而判断该指标对目标决策的影响程度［13］。熵权法计算步骤如下：

（1）将构建的判断矩阵进行数据标准化处理得到标准化矩阵Yij。

（2）计算各指标的熵值Ej。

（3）根据求出熵值，求解各指标权重。

1.4.2 熵权法的改进

上文介绍了传统熵权法的基本原理，通过实际应用、分析，这种传统熵权法具有一定缺陷，当熵值趋近于1时，每个熵间细微的变化都会导致各指标熵权间的成倍变化［14］。如：当取4 个指标的熵值分别为0.999、0.998、0.997、0.996时，这几个指都趋近1，这4 个指标对目标决策的影响程度都相接近。但通过传统熵权法进行计算，这4 个指标的出权重为0.1、0.2、0.3、0.4，其权重成倍数变化，不符合各指标对目标决策的真实影响程度。根据此类情况，本文采用改进的熵权法模型进行计算。步骤如下：

根据权重系数规则，各指标权重相加等于1，同时各指标权重需为大于0小于1的数，该公式均满足此要求。扔取4个指标熵权分别为0.99、0.98、0.97、0.96时通过改进的熵权法计算得出权重为0.209 1、0.236 4、0.263 6、0.290 9可知指标权重不会由于每个熵间的细微变化而导致成倍增长。

1.5 组合权重的计算

考虑到主观权重不能反映数据信息，而客观权重无法体现决策者的主观意愿，从某种意义上讲，主观权重向量和客观权重向量都不是最优的权重向量［15］。因此，为了权重的稳健性，需要进行主客观组合赋权，保证组合后的权重更为合理有效［16］。考虑到主客观权重特性，本文采用乘法合成法进行组合权重。步骤如下：

1.6 利用FCE计算综合评价值

本文采取模糊综合评价法计算水资源承载力最终评价值，模糊综合评价法是借助模糊数学隶属度理论将定性的评价转换成定量评价，使一个受到多方因素制约的对象做出一个清晰、准确的评价。指标类型为“+”的隶属度计算公式如下［17］。

此公式为指标类型为“效益型（越大越好）”的隶属度计算公式，若指标类型为“成本型（越小越好）”将公式中“＞”与“＜”互换位置即可［17］。

2 实例分析

2.1 研究区域概况

芜湖，位于安徽省（E118°21'，N31°20'）。坐落于长三角西南部，地处青戈河、漳河、裕溪河交汇处，是华东重要的工业基地、综合交通枢纽。该市为亚热带湿润季风气候，光照充足，雨量充沛，四季分明［18］。芜湖降雨充沛，年降雨量1 200 mm，但年内降水分布不均，主要集中在春季、梅雨季节和初冬，无霜期每年达219～240 d［18］。

芜湖市虽水资源丰富，但据环保局监测资料显示该地区水污染趋势加剧，青戈河水体污染严重，部门指标超标，出现富营养化、有机物污染等问题［18，19］。且水体污染导致可利用地表水资源减少，水资源供需矛盾等问题［19］。

2.2 数据来源

本文各指标数据来源于芜湖市水务局（https：//shuiwuju.wuhu.gov.cn/）提供的《芜湖市水资源公报》、安徽省统计局（http：//tjj.ah.gov.cn/）提供的《安徽统计年鉴》、以及部分参考文献。

2.3 计算结果

根据上文所介绍的模型，按照第1 节所提供的方法进行计算，计算结果见下表所示。改进的熵权法与传统熵权法权重对比见表2，未赋权的超矩阵见表3，赋权超矩阵见表4，指标权重见表4，ANP 计算指标权重见表5，芜湖市水资源承载力最终权重见表6，芜湖市2006-2016年评价值见表7。

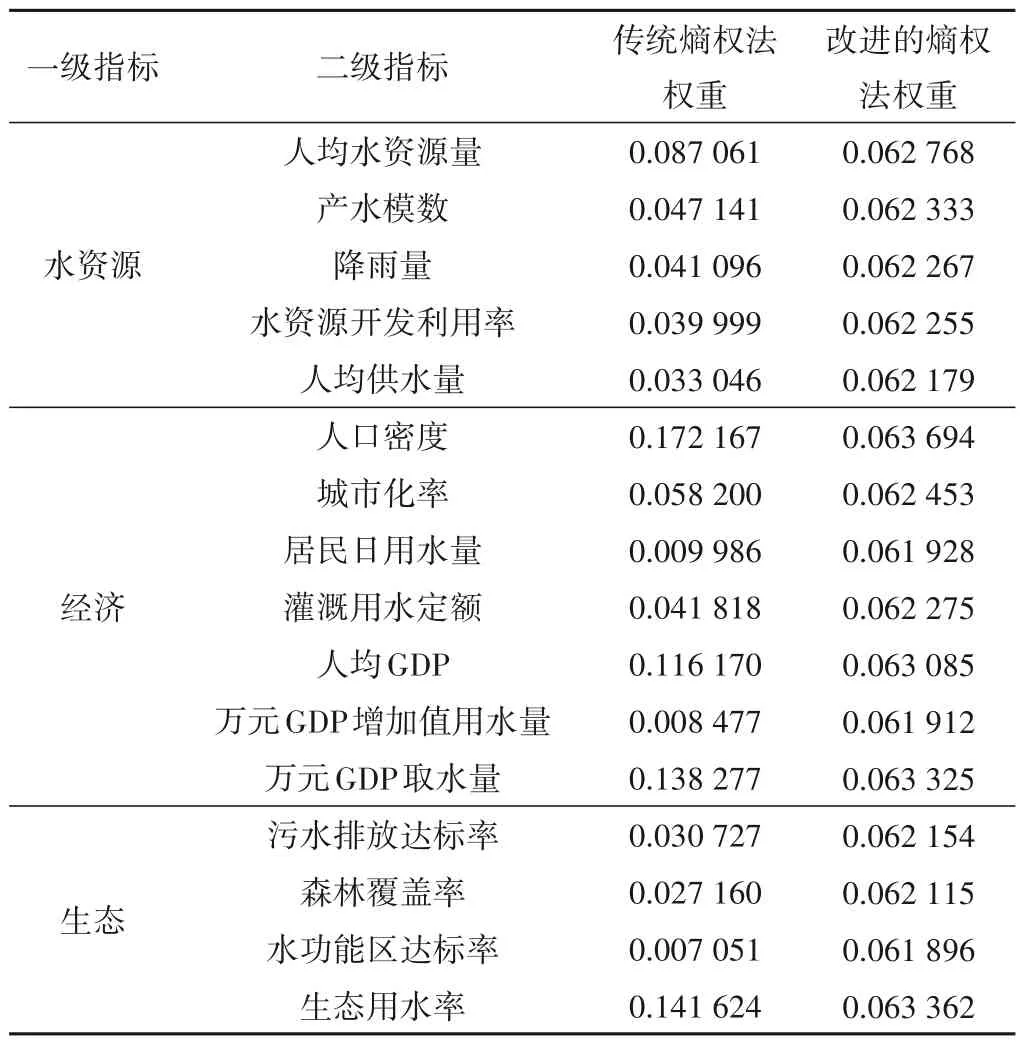
表2 改进的熵权法与传统熵权法权重对比Tab.2 Weight comparison between improved entropy weight method and traditional entropy weight method

表3 水资源承载力评估指标的未赋权超矩阵Tab.3 Unweighted supermatrix of water resources carrying capacity evaluation index

表4 水资源承载力评估指标的赋权超矩阵Tab.4 Weighted supermatrix of water resources carrying capacity evaluation index

表5 ANP 计算指标权重Tab.5 ANP calculation index weight

表6 芜湖市水资源承载力最终权重Tab.6 Final weight of water resources carrying capacity in Wuhu City

表7 芜湖市水资源承载力评价得分Tab.7 Water resources carrying capacity evaluation score of WuHu City

3 讨论

本文通过改进组合赋权模型的水资源承载力评价，充分考虑了芜湖市水资源承载力评价体系间各指标复杂的关系，可以精准地计算出指标权重，能够合理的确定指标间权数分配，提高了指标权重的客观性、精确性、科学性。

本文通过改进的组合赋权模型的对芜湖市水资源承载力进行评价与前人研究成果进行比较，其中孙康等［20］通过层次分析法计算权重得出芜湖市水资源承载力评价值0.4～0.6之间，总体趋势除2011 年、2013 年以外总体上升，水资源承载力处于临界状态。与本文研究成果相比基本相符。

从ANP 空间网络结构来看，各指标层之间存在相互影响关系其簇内节点也存在着相互影响的关系。模型计算结果显示，一级指标层水资源在所有的指标层中重要程度最大，影响其他指标程度最大。在一级指标水资源当中，其各指标权重均在平均值之上，对水资源承载力影响程度较大，其中水资源开发利用率指标影响度最大。一级指标经济中，居民日用水量、人均GDP 影响度大。一级指标生态中，生态用水率影响程度最大。由于降雨量受人为干扰可能性较小，因此人均水资源量、产水模数、水资源开发利用率、人均供水量、居民日用水量、人均GDP、生态用水量与其他指标关联性强，对这些指标进行改变，对其他指标影响最大，水资源承载力提升更加明显。

由图3 可知该区域水资源承载力上升最快为2015 年到2016年，综合评价值上升0.060 9，查询该年数据可知，主要原因是水资源方面：该年降雨充沛，水量丰富，人均水资源量明显提升。经济层面：该年人均GDP 首次突破7 万元，随着节水设施的推广该年万元GDP 取水量首次进入100 m3。生态方面：该年污水排放达标率突破85%，水功能区全部达标。

通过对熵权法的改进优化解决了传统熵权法每个熵间的细微变化而导致权重成倍增长的现象。使计算出的权重更能准确地表现出各数据指标对目标决策的真实影响情况。采用AHP 和改进的熵权法计算组合权重的方法既尊重了专家在以往评价计算中的经验，又客观的结合了数据指标使评价结果更加真实、准确，能够科学的评估区域水资源承载力综合情况，能够对水资源开发利用加以参考作用。

4 结论

采用改进组合权重水资源承载力评价模型对芜湖市水资源承载力进行评价与前人研究结果对比评价结果相符说明该模型在水资源承载力上应用行之有效，该模型评价结果显示芜湖市水资源承载力综合评分位于0.407 1～0.637 0 之间，其最低值2006 年（0.407 1），最高值为2016 年（0.637 0）该研究区域水资源承载力呈上升趋势，说明该区域对于水资源承载力的管理方式行之有效，未来可以继续保持。

根据研究区域实际情况选取指标体系，构建综合评价模型。不仅能够对水资源承载力进行静态评价，还可以对不同年份、不同时期水资源承载力进行动态评价。评价结果相互对比，相互激励。找寻水资源承载力薄弱部位，有针对性地对提升区域水资源承载能力对症下药。