适用于我国水环境管理的5X 综合水量水质模型

罗兰，张艳军，董文逊，邱安妮，宋圆馨，佘敦先

（武汉大学水资源与水电工程科学国家重点实验室，湖北武汉 430072）

0 引言

水量水质模型常可以模拟水量水质指标连续的时空变化过程，对水环境的变化给出预报和预警，对水环境治理具有重要意义，且由于缺乏连续的原位水质监测数据，水量水质模型逐渐成为预测河流及湖泊水质的重要工具。目前常用的水量水质模型主要有WASP（Water Quality Analysis Simulation Program）模型［1，2］、QUAL 系列模型［3，4］、MIKE 模型［5］、EFDC（The Environmental Fluid Dynamics Code）模型［6，7］、Delft3D 模型［8］等，随着水质模型研究的深入与完善，许多学者对综合水质模型进行耦合，使其在水量水质模拟、水环境管理等方面得到了广泛的应用［9］。这些综合水质模型的发展已经比较成熟，但其参数繁多，模拟时需要大量的实测水质数据来设置初始条件和边界条件。由于部分水质数据缺乏，且这些常用的综合水质模型指标体系与我国生态环境部提出的“9+X”（水温、pH、溶解氧、电导率、浊度、高锰酸盐指数、氨氮、总磷、总氮等9 种指标和X 特征指标，X 特征指标为《地表水环境质量标准》（GB3838-2002）表1 基本项目中，除9 项基本指标外，上一年及当年出现过的超过III 类标准限值的指标）、“5+X”（pH、溶解氧、高锰酸盐指数、氨氮、总磷等5 种指标和X 特征指标）指标体系［10］不一致，导致这些水质模型在我国河流及湖泊应用时十分困难。

Costa 等［11］认为现在使用的综合水质模型过于复杂，应用困难，巨大的数据需求会耗费时间和经济成本，并且在缺乏数据时使用复杂的模型降低了水质预测的可靠性。例如Delft3D模型的水质模块指标包括氯化物、大肠杆菌、生化需氧量、温度、含氮有机物、无机磷酸盐、硝酸盐、悬移质泥沙、藻群和重金属元素等，只有具备完整资料才能进行水质模拟，在应用上存在一定的局限性［12］。吴凡杰等［13］在应用Delft3D 模型进行排污策略研究时指出该水质模型所涉及的水质生化过程比较复杂且一般为经验公式，实际应用时模型参数的设定以及模型调试过程的工作量巨大。QUAL-II 模型综合描述以下13 种水环境变量：溶解氧、生化需氧量、水温、叶绿素-a、氨氮、亚硝酸盐氮、硝酸盐氮、可溶性磷、大肠杆菌等，其中的相关参数高达20 多个，水质模拟时也需要大量的实测水质数据，虽然模型结构合理，理论精度高，但是实际应用仍然十分难［14］。且QUAL-II 模型建模时对于河段支流个数以及计算单元数有较大的限制［15］。WASP 模型可以模拟氨氮、生化需氧量、溶解氧、浮游植物和有毒物质等［16］，虽然其水质指标体系比较全面，但是其中很多水质指标在我国水环境管理中使用频率很低，导致实际应用时缺乏数据支持。EFDC 水质模型包含22 个水质状态变量，考虑了藻类、溶解氧、磷、二氧化硅、有机碳和化学需氧量等多种水质组分，并且根据水质变量的动力学复杂程度设置了5 种水质模块以供选择［17，18］：模块0 基于WASP5 水质模型的动力学基础，只考虑水体中的有机碳、有机磷和有机氮类；模块1动力学复杂程度居中，综合考虑有机碳、有机磷和有机氮中的不稳定型和难降解型水质指标；模块2采用CE-QUAL-ICM 水质模型［19］，考虑的水质指标更为全面；模块3 基于CE-QUAL-ICM 水质模型［20］进行扩展，水质变量包含溶解型、颗粒型、不稳定型以及难降解型的有机碳、有机磷和有机氮；模块4考虑的水质变量动力学方程比较复杂。EFDC 模型在水质模拟方面将一个庞大的模型体系分解为多个小块，在使用时可以根据需求以及水质变量耦合作用的复杂程度选择相应的子模块，但是其各个子模块仍然与我国水环境管理的评价指标匹配程度不高，且对于其子模块的选择也存在一定的困难。综合来看，这些常用的综合水质模型指标体系与我国水环境管理要求不一致，这种不匹配给我国水环境管理，以及水质模型的应用和发展，都带来一定的障碍。Ejigu M T 指出在大多数发展中国家，统一的水质模型标准化体系尚未得到认可，当前较为成熟的国外综合水质模型应用困难，另一方面，模型的复杂性、水质实测数据的缺乏和数据质量差也是水质模型应用的限制因素［21］。因此，根据生态环境部提出的“5+X”指标体系对水质模型的指标体系进行规范，建立适用于我国水环境管理的标准化水质模型至关重要。

为满足地表水质“5+X”［10］的评价要求，提高综合水质模型的实用性，本文提出了一种适用于我国水环境管理的5X 综合水质模型。该模型简化了水体中各种水质组分之间复杂的耦合作用关系，综合模拟以下7 种水质指标：溶解氧、高锰酸盐指数、叶绿素-a、氨氮、硝酸盐氮、总磷和X 特征指标，使其在易用性和科学性上取得平衡。同时，将其与基于DEM的二维水动力模型耦合，形成适用于我国水环境管理的5X 综合水量水质模型。以九江市八里湖为例，验证了该模型的实用性和可靠性。最后，将该模型应用于九江模拟器，作为其重要的模型支撑。

1 研究区概况及研究数据

1.1 研究区域概况

八里湖流域位于九江市区西南部，流域汇水面积273 km2，湖区集水面积约18 km2。八里湖湖底平坦，湖底高程约13～15 m，常水位17.5 m。八里湖流域内水系比较丰富，在其东侧、西侧和南侧均有来水，其北侧的新开河和龙开河与长江相连，最终将湖水汇入长江（如图1）。八里湖与庐山相隔很近，庐山上的水一部分流入八里湖，是八里湖的主要水量来源。八里湖流域地处亚热带季风气候区，气候温湿，四季分明，春、夏季常逢冷暖气流交替，阴雨连绵；夏、秋之交，常受副热带高压控制，晴热少雨［22］。

图1 八里湖周边水系图Fig.1 Map of river system around Bali Lake

1.2 研究数据

模型所需的基础数据主要有水下地形资料、水质资料和气象资料。水下地形数据根据实测点位水深数据，采用自然邻点插值法插值得到［23］（如图2）；水质实测数据包括2020 年7 月1日至7 月29 日早上8∶00、下午2∶00 和晚上8∶00 八里湖2 个水质监测点的氨氮、溶解氧、高锰酸盐指数、总磷、叶绿素-a 浓度数据，八里湖整体水质变化不大，但十里河入八里湖口处在夏季蓝藻暴发现象屡有发生，且该处存在排污口，是敏感区域，故2 个水质监测点分别选在八里湖十里河入湖口和十里河拐角处；流量数据包括八里湖各个出流口和入流口的流量实测值；气象数据为中国气象数据网上的共享数据，包括气温、光照和风速。

图2 八里湖水下地形图Fig.2 Underwater topographic map of Bali Lake

2 模型构建

为对九江市两河及八里湖区域多要素的城市水循环和水环境过程进行综合模拟，九江模拟器需综合考虑山区、城市、城内外河流湖泊、长江之间的水量与污染物的交互循环过程，耦合集成城市水文过程、河湖水环境过程、城市面源污染过程以及城市污水处理厂管网一体化调度管理过程，如图3 所示。作为九江模拟器的一部分，适用于我国水环境管理的5X 综合水量水质模型需对研究区域的水环境系统进行模拟和评价，以及对水华暴发问题进行预警。该模型的主要研发目标是使其满足我国地表水质“5+X”［10］的评价要求，使模型简便易用和可移植，最后应用于九江模拟器。该模型包括水动力模块和综合水质模块，在网格层面上与数字高程模型（Digital Elevation Model，DEM）进行耦合。其中5X 综合水质模型能够同时模拟溶解氧、氨氮、总磷、高锰酸盐指数等水质指标，并且对叶绿素-a进行模拟，对水华暴发进行预警。

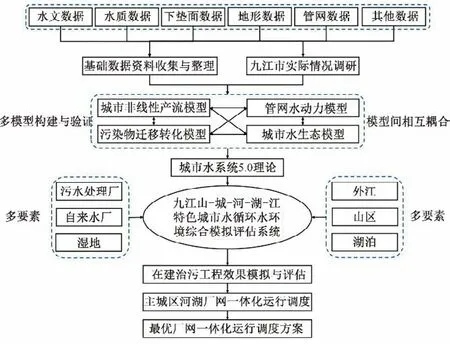
图3 九江模拟器模型原理Fig.3 The model principle of Jiujiang simulator

2.1 水动力模型

本文所使用的水动力数学模型是由连续性方程和动量方程构成的二维方程组。其中连续性方程如式（1）所示［24］：

x方向上的动量方程如式（2）所示：

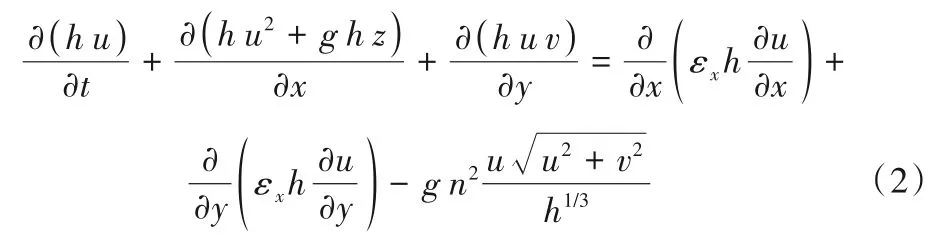
y方向上的动量方程如式（3）所示：

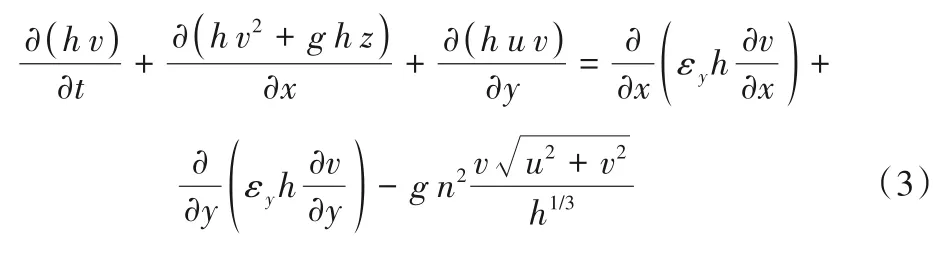
式中：h代表研究区域水体的水深，m；t为模型模拟的时间步长，s；u、v代表平面二维坐标系横向和纵向的流速，m/s；εx、εy分别为x、y方向的涡动黏滞系数，m2/s；g为重力常数；n为糙率；q为支流入流的单宽流量，m2/s。

2.2 5X综合水质模型

2.2.1 基本方程

本文的综合水质模型采用对流扩散方程描述水质的变化情况，并且在DEM网格基础上将综合水质模型和二维水动力模型耦合求解。对于任意一个水体污染物的浓度C，可得到如式（4）所示的平面二维水质迁移转化基本方程：

式中：∑Si为湖泊水体污染物的源项，包括内部源漏项和外部源漏项；Ex为x方向的分子扩散系数、紊动扩散系数和离散系数之和；Ey为y方向的分子扩散系数、紊动扩散系数和离散系数之和。

对于任意一种水质组分都可以采用如式（4）所示的二维水质迁移转化基本方程，但是不同的水质变量的源漏项不同，下面将分别介绍综合水质模型所采用的几种水质变量的源漏项［25］。

式中：Sint为水质变量的内部源漏项；Sext为水质变量的外部源漏项。

2.2.2 各水质变量源漏项

《“十四五”国家地表水监测及评价方案（试行）》中提出国家地表水质按照“5+X”的方案进行评价，评价指标为pH、溶解氧、高锰酸盐指数、氨氮、总磷等5 项基本指标及该断面的“X”特征指标［10］。且对于湖泊进行水质评价时，一般还要考虑湖泊的富营养化程度，水体富营养化程度可以采用综合营养状态指数法（TLI）评价［26］，评价指标包括总磷、总氮、高锰酸盐指数和叶绿素-a 等。为满足地表水体水质评价和营养状态评价的需求，更加详细地描述水质的变化以及其中各种水质组分的相互影响关系，本文提出了一种适用于我国水环境管理的5X 综合水质模型，综合描述以下7种水环境变量：叶绿素-a、氨氮、硝酸盐氮、总磷、高锰酸盐指数、溶解氧和X特征指标，并且对这7种水环境变量进行耦合求解，pH 值一般通过实际监测得到，采用水质模型模拟意义不大，故该水质模型不考虑pH 值的模拟。5X 综合水质模型指标体系与“5+X”指标体系、综合营养状态指标体系基本一致，实际应用中可以直接根据这些水质变量的模拟结果对地表水质状态和营养状态进行初步预测。

在QUAL-II模型的基础上，5X综合水质模型进行了系统性的重构和概化（如图4）。其中具体内容包括：①采用叶绿素-a反映水体中藻类生物的生长与代谢过程；②将QUAL-II 模型中氨氮、亚硝酸盐氮和硝酸盐氮之间的转化关系进行概化，只考虑氨氮最终氧化为硝酸盐氮这一过程，减少初始条件数据需求量；③将QUAL-II 模型中的正磷酸盐替换为总磷；④将QUALII 模型体系中的BOD 换算为高锰酸盐指数进行模拟；⑤考虑水体中溶解氧的平衡以及各种耗氧、复氧过程。

图4 水质模拟组分耦合作用关系图Fig.4 The coupling relationship diagram of water quality simulation components

5X 综合水质模型描述了以水体溶解氧的平衡和水体中藻类微生物的生长代谢为核心的多个水质组分之间的相互作用关系。溶解氧的补充主要考虑水体中藻类光合作用产氧和大气复氧，溶解氧的消耗主要考虑含碳有机物的生物降解耗氧以及氨氮的硝化过程耗氧。硝酸盐氮和磷作为养分被水体中的藻类吸收，同时，藻类代谢会生成氨氮和磷，这些水质组分在藻类的作用下形成循环。

（1）随着湖泊资源的开发利用，很多湖泊出现了富营养化现象，部分湖泊发生水华暴发现象［27］，叶绿素-a 的含量是反映水体富营养化程度的重要指标，对叶绿素-a进行有效监测和模拟，有助于防止水华暴发和水质进一步恶化［28］。叶绿素-a的浓度与藻类生物量的浓度成正比，为了建立叶绿素-a与其他水质组分之间的关系，用一个转换系数反映叶绿素-a与藻类生物量的转换关系，如式（6）所示：

水体中藻类的源漏项如式（7）所示：

式中：SA为藻类的源漏项，mg/（L·d）；Ca为叶绿素-a 的浓度，μg/L；CA为藻类生物量的浓度，mg/L；α0为转换系数；μ为藻类的比生长速率，1/d；ρA为藻类代谢速率常数，1/d。

藻类的比生长率与可用的营养盐和光照强度等有关，可用式（8）计算：

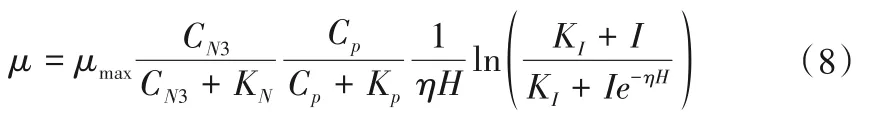
式中：μmax为最大比生长率，1/d，与温度T有关，可由μmax=μmax(20)θT-20修正；CN3为硝酸盐氮的浓度，mg/L；Cp为总磷的浓度，mg/L；KN为硝酸盐氮的半速常数，mg/L；KP为总磷的半速常数，mg/L；KI为光照的半速常数，g·W/m2；η为消光系数，1/m；I为光照强度，g·W/m2。

（2）氨氮。氨氮是水体中主要的耗氧污染物之一，氨氮含量超标会导致水体富营养化，不利于水生生物的生长，因此在水质评价中监测氨氮的含量很有必要［29］。

式中：SN1为氨氮的源漏项，mg/（L·d）；CN1为氨氮浓度，mg/L；α1为藻类生物量中氨氮的比例；KN1为氨氮氧化为硝态氮的速率常数，1/d。

（3）硝酸盐氮。氨氮、亚硝酸盐氮和硝酸盐氮在水体中能互相转化，且与总氮有着密不可分的关系，地表水体中的亚硝酸盐氮与硝酸盐氮存在比值关系［30］，亚硝酸盐氮与硝酸盐氮的源漏项之和可表示为：

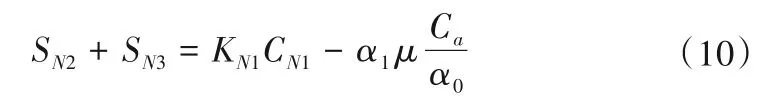
式中：SN2为亚硝酸盐氮的源漏项，mg/（L·d）；SN3为硝酸盐氮的源漏项，mg/（L·d）。

故硝酸盐氮的源漏项为：

式中：β1为水体中亚硝酸盐氮与硝酸盐氮含量中硝酸盐氮的比例。

（4）总磷。正磷酸盐不是常用地表水质监测指标，其浓度数据难以获取，而总磷的监测数据比较丰富，在该综合水质模型中，考虑总磷和藻类的相互影响关系，如式（12）所示：

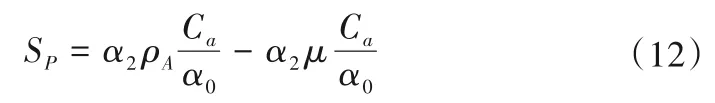
式中：SP为总磷的源漏项，mg/（L·d）；α2为藻类生物质量中磷所占的比例。

（5）高锰酸盐指数。高锰酸盐指数是反映水体水质的综合指标，在进行水质监测时其在数小时内就能完成精准测量，而BOD 则需要五天且测量步骤较为复杂。因此，高锰酸盐指数在我国的水环境管理中得到了普遍的应用。在本文的综合水质模型中，可以通过经验关系将QUAL-II模型体系中的BOD 换算为高锰酸盐指数进行模拟。BOD 的变化速率按一级反应动力学考虑，如式（13）所示。地表水体中的BOD 与高锰酸盐指数之间存在一定的比值关系，一般认为BOD 与高锰酸盐指数比值在0.1～0.7之间［31］。

式中：L为BOD 浓度，mg/L；LC为高锰酸盐指数值，mg/L；K1为BOD降解速率常数，1/d；β2为高锰酸盐指数与BOD的比值。

（6）溶解氧。溶解氧是水体中重要的水质因子，它不仅影响水生动植物的生长发育，还影响水中有机污染物的降解，是水质模拟的核心组分。

式中：SC为溶解氧的源漏项，mg/（L·d）；C为溶解氧浓度，mg/L；Cs为饱和溶解氧浓度，mg/L；α3为藻类光合作用产氧率；α4为藻类呼吸作用耗氧率；K2为复氧系数；α5为单位氨氮转化为硝酸盐氮的耗氧率。

（7）X特征指标。“十四五”国家地表水监测及评价方案中评价指标包含X 特征指标，其需要结合水污染防治工作进行动态调整。将X 特征指标概化为可降解的水体污染物，其源漏项可写为：

式中：SX为特征指标X 的源漏项，mg/（L·d）；KX为特征指标X 的降解速率常数，1/d；CX为特征指标X的浓度，mg/L。

2.3 模型求解方法

适用于我国水环境管理的5X 综合水量水质模型需要使用DEM 地形数据，而DEM 由矩形网格构成，采用基于同位网格算法［32］的有限体积法离散二维动量方程组和水质迁移扩散方程，把离散后的横向速度U、纵向速度V 和水深H 同时储存于同一网格节点上，系统中只存在一种类型的控制体积。有限体积法（FMV）又称有限控制容积积分法，该方法把计算区域离散为若干点，以这些点为中心，把整个计算区域划分为若干互相连接但不重叠的控制体［33］。采用SIMPLEC 算法［34］对DEM 有效网格格点上的水深进行校正，计算前对水体区域进行初步识别，运用加壳算法生成边界，运用干湿法处理水体运动过程中涨水和落水而导致水体边界改变的问题。最后采用三对角矩阵算法（TDMA）和交替方向隐式迭代算法（ADI）求解离散方程组［35，36］。

3 模型率定与验证

3.1 模型参数确定

参数的选取会对模型的模拟精度有影响，若参数选取不合适，将会直接导致模拟结果误差增大。但是由于目前八里湖区域没有具体的资料，也未开展室外实验测定相关的参数，故本文对于模型参数的取值主要根据经验公式计算或者采用以往的经验移用。

糙率的取值对于水流的计算有很大的影响，根据经验可知八里湖区域水动力模型糙率取值范围为0.025～0.033。涡动黏滞系数可以采用混合长度（掺长）模型公式计算，如式（17）所示。污染物在水体中的扩散作用主要为离散作用，污染物的综合扩散系数可以采用经验公式进行计算，如式（18）所示［25］。

式中：κ为卡门常数，取为0.4；z为计算水位。

式中：H为平均水深；u*=；J为水力坡降；u为断面平均流速。

采用经验公式进行计算，水动力模块参数取值如表1所示。

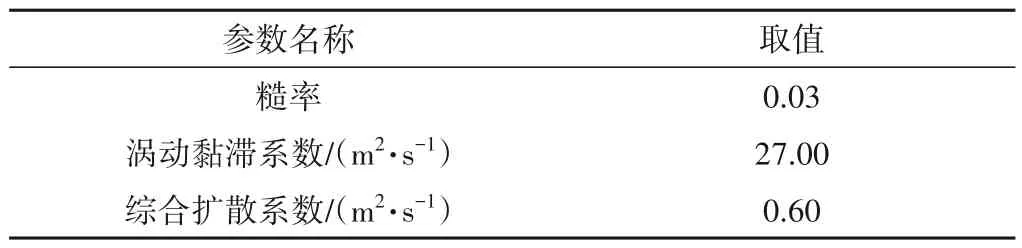
表1 水动力模块主要参数设置Tab.1 Main parameters setting of hydrodynamic model

根据八里湖水质监测资料，选取高锰酸盐指数、氨氮、总磷、溶解氧、叶绿素-a作为水质计算的代表指标，各种污染物的降解系数取值主要根据对模型的应用经验以及前期在八里湖区域的实地考察来确定，九江市中心城区水系统数值模拟平台构建及水环境目标可达性评估专题报告中对八里湖污染物降解系数进行了率定，给出了各种污染物降解系数的取值范围，高锰酸盐指数降解系数取值为0.08～0.15 d-1，氨氮降解系数取值为0.04～0.08 d-1，总磷降解系数取值为0.02～0.04 d-1。其他水质参数取值如表2所示。

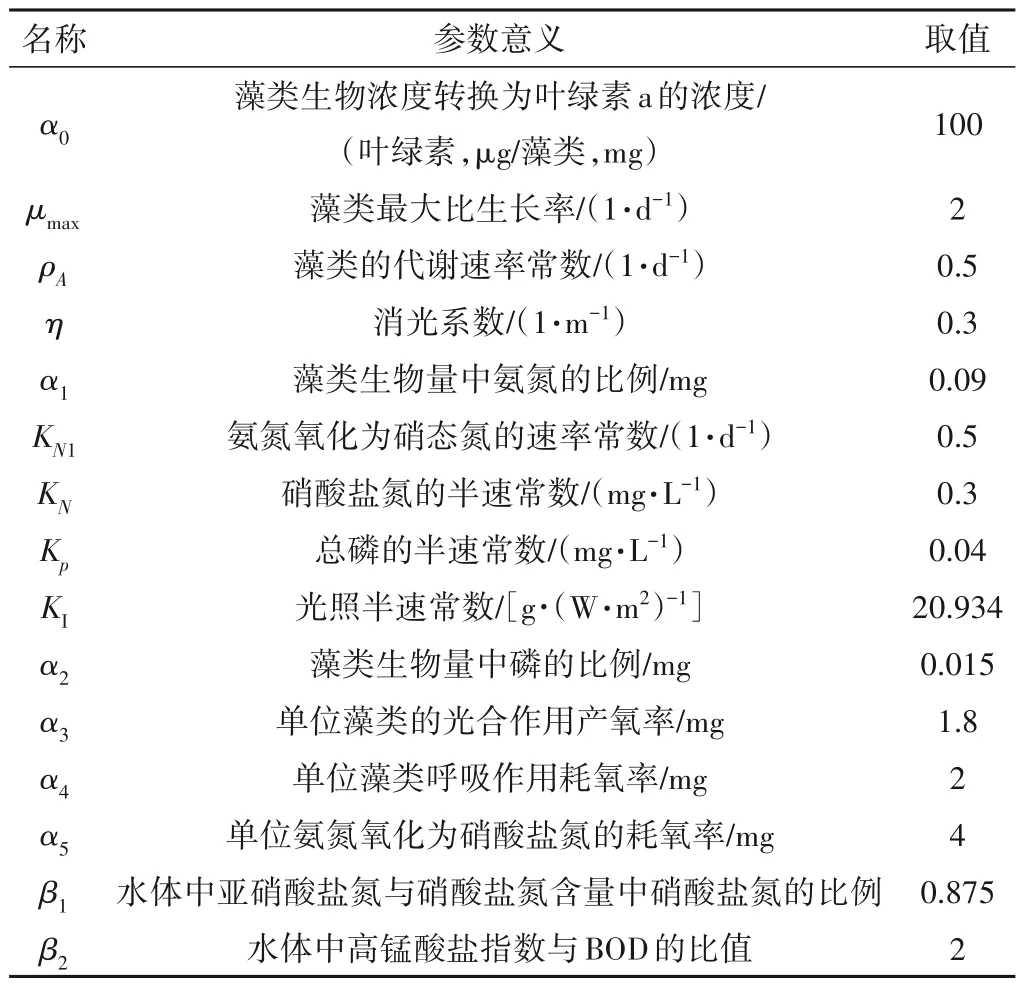
表2 水质模块主要参数设置Tab.2 Main parameters setting of water quality model

3.2 水动力验证结果

根据八里湖实际情况和计算的精度要求，设置计算网格大小为10 m×10 m，共划分283 122 个正方形网格。计算初始时刻给定八里湖的全局初始水位17.78 m 和初始水深4.4 m，设置八里湖各种水质组分的背景浓度，并且在初始时刻认为水体处于静止状态，即U=0、V=0，对八里湖水动力情况进行模拟。

百分比偏差（PBIAS）测量的是模拟数据比观测到的数据更大或更小的平均趋势，PBIAS的最优值为0，低幅值表明模型模拟准确，该指标可以对模型的性能进行定量评价［37］。国内外都有学者使用该方法对水质模型的模拟结果好坏进行评判，例如张雨航等［38］采用PBIAS方法对基于MIKE21 模型的总氮模拟模型进行评价，模型总体达到优秀结果，表明MIKE21模型可以用于水库总氮的预测研究中；顾杰等［39］采用PBIAS方法对MIKE11 水质模块的COD 模拟结果进行定量评价，表明该模型具有很好的预测效率，模拟效果可靠。

PBIAS（百分比偏差）由式（19）计算［37］：

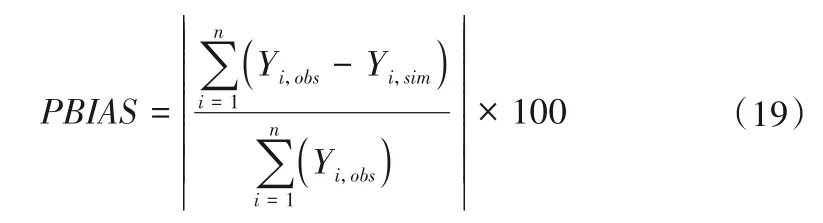
式中：Yi，obs为实测值；Yi，sim为模拟值；n为模拟数据总数。

对于水动力模拟，模型的预测效率分为：PBIAS小于10 时优秀，PBIAS在10～15 范围内为良好，PBIAS在15～25 范围内为满意，PBIAS大于25 时不满意；对于污染物模拟，模型的预测效率分为：PBIAS小于25 时优秀，PBIAS在25～40 范围内为良好，PBIAS在40～70 范围内为满意，PBIAS大于70 时不满意［39］，如表3所示。

表3 PBIAS方法性能等级Tab.3 PBIAS method performance level

采用八里湖水位实测数据，与同期水位模拟数据进行对比，根据式（19）计算水位模拟结果的PBIAS值，模拟结果如图5所示。由图5可知，八里湖模拟水位和实测水位趋势比较接近。水位模拟值与实测值的相对误差范围为0.10%～2.80%，水位模拟相对误差平均值为0.27%，PBIAS值为0.95%，水动力模拟效果为优秀。

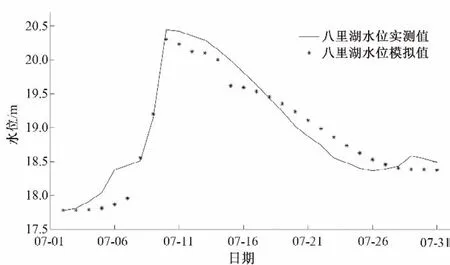
图5 八里湖水位验证结果Fig.5 Water level validation results of Bali Lake

八里湖的流场模拟情况如图6所示。八里湖流场整体趋势是从南向北流动，在八里湖北半湖的东侧和西侧分别有支流汇入；八里湖南半湖入口处有较大的涡旋，十里河入八里湖口处也有少量的涡旋。总体上来说，八里湖流场模拟结果符合实际情况。

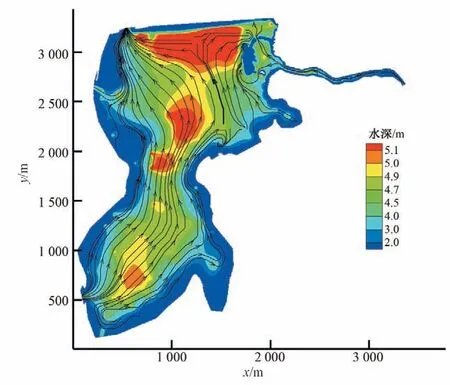
图6 八里湖流场模拟结果Fig.6 Flow field simulation results of Bali Lake

3.3 水质验证结果

水质验证采用2020 年7 月的水质监测数据与同期水质模拟数据进行对比，主要考虑的水质指标有氨氮、溶解氧、高锰酸盐指数、总磷、叶绿素-a，水质指标实测值与模拟值数据对比情况如图7 所示。由图7 可知水质模拟总体情况比较好，对比八里湖两个监测点位的实测值和模拟值，溶解氧、高锰酸盐指数和总磷的趋势比较接近，模拟相对误差较小，氨氮与叶绿素-a的相对误差大一点，但是总体也在可接受的范围内。根据率定验证结果可知模拟水质的时空分布情况与实际调研获得的水质规律比较一致，说明该模型可以用于八里湖区域进行水质模拟研究。

图7 水质组分实测值与计算值对比Fig.7 Comparison of measured value and calculated value of water quality components

根据式（19）计算水质模拟结果的PBIAS值，不同污染物的PBIAS值如表4所示，各水质组分模拟结果的相对误差如表5所示。由表4、5计算结果可知，溶解氧、高锰酸盐指数和总磷模拟结果的PBIAS值均小于25%，平均相对误差值小于20%，模拟结果优秀；氨氮模拟结果的准确程度不如上述几种污染物，但是模拟结果根据百分比偏差法判断也处于良好水平；叶绿素-a模拟结果的准确程度相对来说比较差，平均相对误差在40%左右，性能等级为满意。模型总体对于各种水质组分的模拟比较准确，对所选择的5种水质组分的模拟是可行的，模拟效果比较可靠。

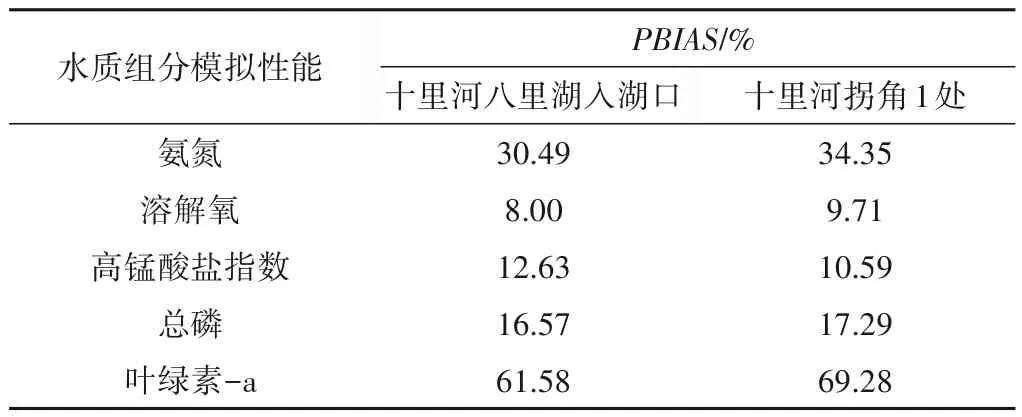
表4 水质指标模拟结果PBIAS值Tab.4 The PBIAS value of water quality index simulation results

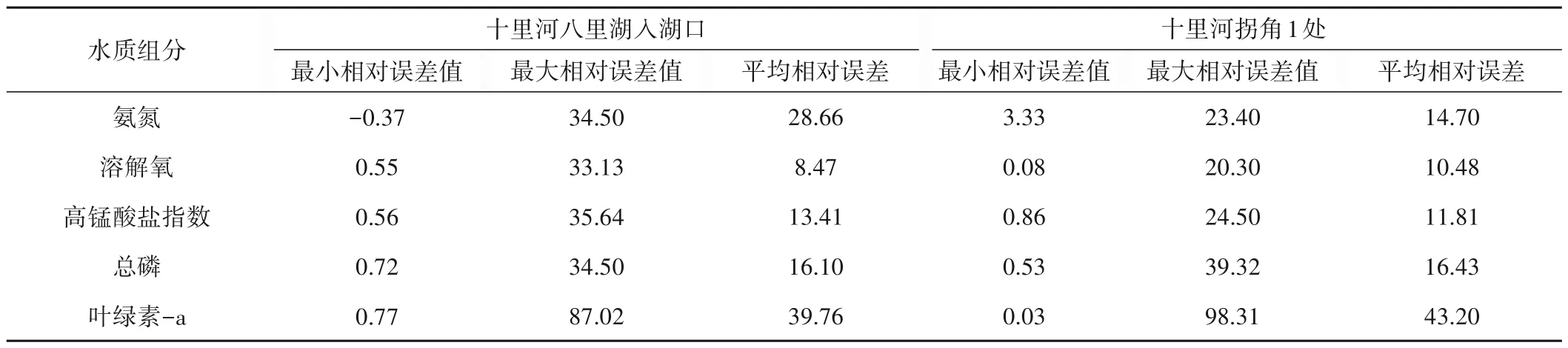
表5 水质指标模拟值与实测值相对误差 %Tab.5 The relative error between the simulated value of water quality components and the measured value

八里湖各种水质组分的浓度场模拟情况如图8所示。高锰酸盐指数、氨氮、总磷在整个湖泊中分布规律基本一致，在入口污染物的影响下，八里湖的水质会变差。从图上也可以看出八里湖氮磷污染比较严重，氨氮、总磷基本上为Ⅳ类～Ⅴ类水的水平，高锰酸盐指数的情况相对来说较好，水质组分模拟结果与实际水质调研情况一致。湖泊中叶绿素-a 的浓度能够反映湖泊内藻类的生长情况，张家瑞等［40］通过研究分析认为当水体中叶绿素-a 的含量超过30 μg/L 的时候水域会暴发水华。由图8可知，在十里河入八里湖湖口处叶绿素-a 浓度比较高，高于水华暴发的阈值，可能会出现水华暴发的现象。经过实际考察可知八里湖入口处在2020年夏季发生过水华暴发事件，模拟结果与实际情况相符合。

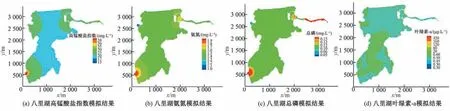
图8 八里湖各水质组分浓度场模拟结果Fig.8 Simulation results of concentration field of various water quality components in Bali Lake

4 讨论

本文建立的适用于我国水环境管理的5X 综合水量水质模型，仍有一些问题值得讨论如下：

（1）D N Moriasi［37］给出了百分比偏差法判断模型模拟效果的方法，认为对于水动力模拟，模型的PBIAS小于10时优秀，对于污染物模拟，模型的PBIAS小于25时优秀。该模型水动力模拟效果优秀，水位模拟值与实测值的相对误差范围为0.09%～2.79%，水位模拟相对误差平均值为0.27%，PBIAS值为0.95%，远低于10%；水质模拟总体效果优秀，其中溶解氧、高锰酸盐指数和总磷的模拟值与实测值吻合良好，模拟结果的PBIAS值均小于25%，氨氮模拟结果根据百分比偏差法判断处于良好水平，叶绿素-a模拟结果的性能等级为满意。

（2）相较WASP 模型和QUAL-II 模型等综合性水质模型，5X综合水量水质模型水质指标设置比较合理，兼顾了模型的实用性和科学性，更加适用于我国水环境模拟；但是QUAL-II 模型和WASP模型考虑的水环境过程更加完整，其科学性更强。

（3）5X 综合水量水质模型仍有部分局限性，其未考虑底泥释放、大气沉降等因素对水体各种水质组分浓度的影响，使得模拟结果存在一定误差。且使用的水下地形数据不够精确，对模型模拟结果也会产生影响，有待进一步提高。

（4）本文对QUAL-II 综合水质模型进行重构和概化时，引入了两个新参数：水体中亚硝酸盐氮与硝酸盐氮含量中硝酸盐氮的比例β1、高锰酸盐指数与BOD 的比值β2，由于这两个参数具有较大的不确定性，可能会对模型结果产生影响，值得进一步分析。

5 结论

为解决国外综合水质模型在国内部分地区应用困难的问题，满足地表水体水质评价和营养状态评价的需求，本文提出了一种适用于我国水环境管理的综合水质模型，对各种水质组分的耦合作用关系进行了重构和概化，在此基础上耦合基于DEM 的二维水动力模型，最终建立了适用于我国水环境管理的5X综合水量水质模型。该模型的指标体系设置合理，与生态环境部提出的“5+X”评价指标一致，且数据需求量少，应用便捷；模型的模拟准确度高，可以模拟水体的水动力情况和水质分布情况，对于受污水体水环境综合整治工作的开展具有重大的现实意义。将其应用于九江市“山-城-河-湖-江”综合模拟器，为解决九江市目前存在的水环境问题出谋划策，对实现生态文明建设和长江大保护战略有指导意义。