单层CrI3 电荷输运性质和光学性质应变调控的第一性原理研究*

王娜 许会芳 杨秋云 章毛连 林子敬

1) (安徽科技学院电气与电子工程学院,蚌埠 233000)

2) (中国科学技术大学物理系,合肥 230000)

通过应变调控二维材料的电学性质和光学性质是设计新型二维电子和光电子器件的重要环节,也是后摩尔时代薄膜器件设计中的关键技术.薄膜CrI3 具有铁磁和层间反铁磁的独特性质,但是关于应变调制其电学性质和光学性质的研究未见报道.本文采用高精度杂化密度泛函理论研究了面内单双轴应变对单层CrI3 载流子迁移率和介电函数的调控规律,研究结果与已有的实验和理论值符合较好.计算发现: 单层CrI3 载流子迁移率非常小,均在10 cm2·V—1·s—1 以内;与拉伸应变相比,双轴压缩应变可以显著提升迁移率;当双轴压缩应变量增至8%时,沿锯齿方向电子迁移率增至174 cm2·V—1·s—1,达到了MoS2 水平.可见光区介电函数虚部x (y)方向I 号吸收峰强度随双轴拉伸应变量增加明显增强,而z 方向几乎没有变化;可见光区x (y)和z 方向的介电函数虚部曲线开始攀升的起点对应的光子能量均随双轴压缩应变量增加明显减小,且所有吸收峰呈现明显的红移.结果表明,应变可以明显提升单层CrI3 的电荷输运性能和可见光区的光学性能.

1 引言

2017 年,关于单层CrI3和双层Cr2Ge2Te6铁磁性的实验报道[1,2],既打破了50 年前 Mermin等[3]提出的二维各向同性海森伯模型在非零温度下不会存在自发长程磁序的定理,又大大激发了人们对薄膜CrI3的磁学、电学和光学等性质的应变调制的研究热情.Sivadas等[4]研究发现双层CrI3层间堆垛结构的改变可以实现其在铁磁性 (ferromagnetic,FM)与反铁磁性(antiferromagnetic,AFM)间的反复转换,使低维CrI3磁性的机械调制成为可能.Guo等[5]研究发现应变工程可以调节单层CrI3的磁光克尔效应,磁光克尔谱随垂直薄膜方向的压缩应变发生红移,而随拉伸应变发生蓝移.Webster 和Yan[6]研究了单层CrI3基于自旋轨道耦合 (spin-orbit coupling,SOC)的磁性各向异性,计算发现磁性各向异性能 (magnetic anisotropy energy,MAE) 随双轴拉伸应变量增加而减小.Bacaksiz等[7]计算了双轴应变下单层CrI3的德拜温度、磁滞回线和MAE 的变化规律,研究发现德拜温度随拉伸应变量增加而增大.

薄膜CrI3的电荷输运性质和光学性质的变化取决于其电子能带结构的改变.关于电子能带结构的实验测量存在很多不确定性,而基于密度泛函理论[8](density functional theory,DFT) 的第一性原理计算展现出无可比拟的优势.但是,采用一般的交换关联泛函[9]计算单层CrI3的电子结构出现了很多矛盾的地方.例如,Wu等[10]利用含强关联修正的广义梯度近似方法(generalized gradient approximation add on-site repulsionU,GGA+U)计算了面内应变下CrI3的电子结构,研究发现—10%—1.8%双轴应变范围内CrI3为铁磁材料;Mukherjee等[11]通过含强关联修正的局域密度近似方法(local density approximation add on-site repulsionU,LDA+U)理论研究了面内应变下单层CrI3的电子结构和磁学性质,计算发现—12%—12%双轴应变范围内CrI3为铁磁材料;Pizzochero和Yazyev[12]运用 GGA+U密度泛函理论计算了单层CrI3在不同应变下的磁相图,研究发现0 到—5%双轴应变范围内CrI3为铁磁材料,而在—5%到—8%双轴应变范围内CrI3为反铁磁材料.

杂化泛函HSE06 (Heyd-Scuseria-Ernzerhof,HSE) 被公认为是计算半导体材料电子能带结构和光学性质最精准的方法,近几年来被广泛应用[13-15].Zhang等[16]利用HSE06 研究了块体及单层三卤化铬的电子能带结构、磁学和光学等性质.晶体CrI3和CrBr3带隙的计算值 (1.28 eV 和2.40 eV)与实验值 (1.2 eV[17]和2.1 eV[18])非常接近;晶体CrBr3和CrCl3介电函数虚部在低频区的计算结果与实验值[19]十分符合.文献[16]还发现单层CrI3可以吸收可见光,但是对应变调控单层CrI3的电荷输运性质和光学性质没有做进一步研究,其他文献也未见报道.为此,本文利用高精度杂化泛函HSE06 对单层CrI3进行了系统计算,特别是研究应变对其电子能带结构、电荷输运性质和可见光区的光学性质的调控规律,以期为CrI3异质结及其界面的量子调控的实验研究提供理论基础.

2 计算方法

采用基于密度泛函理论的Viennaab initiosimulation package 5.4.4 (VASP 5.4.4)软件包[20]系统计算了应变下单层CrI3的晶体结构、电子结构、电学性质、光学性质和磁学性质.首先,采用基于Perdew-Bueke-Ernzerhof (PBE)的广义梯度近似GGA 作为交换关联泛函[21]进行结构优化和力学性质研究,所有计算均考虑了自旋极化.然后,采用由25%的Hartree-Fock 交换关联泛函和75%的PBE 交换关联泛函组成的杂化泛函HSE06 计算晶体的电子态密度(density of states,DOS)、能带结构和介电函数.最后,运用形变势理论[22-24]给出本征载流子的迁移率µ,考虑自旋轨道耦合作用分析了MAE.平面波[25]截断能取值为390 eV,真空层厚度取值为15 Å (1 Å=10—10m).采用以Γ为中心的网格[26]积分布里渊区,其中原胞 (图1红色实线区域(a),有2 个Cr 原子(紫色球)和6 个I 原子(蓝色球)) 取值为8×8×1,晶胞 (图1 灰色虚线区域(b)—(d),均包含4 个Cr 原子和12 个I 原子) 取值为8×4×1.原子位置优化和电子自洽场迭代的收敛标准分别为0.01 eV/Å和10—7eV.

图1 单层CrI3 的结构图及原胞(a),AF-Néel 晶胞(b),AF-stripy 晶胞(c)和AF-zigzag 晶胞(d)Fig.1.Atomic structure of CrI3 monolayer together with unit cell (a),AF-Néel crystal cell (b),AF-stripy crystal cell (c) and AFzigzag crystal cell (d).

3 结果与分析

3.1 晶体结构

单层CrI3的结构如图1 所示,沿〈100〉和〈010〉晶向的侧视图说明单层CrI3为层状结构,I 原子(紫色小球)位于上下两层,Cr 原子(蓝色小球)位于中间层.每个Cr 原子与最近邻的6 个I 原子构成八面体结构,其中Cr 原子位于体心处,I 原子位于八面体的6 个顶点处.从单层CrI3的俯视图中可见,x方向Cr 原子的排布呈锯齿状(zigzag,zig),而y方向Cr 原子分布呈扶手椅状(armchair,arm).图1(a)为铁磁态原胞结构示意图,等价的2 个Cr 原子具有相同的自旋方向;图1(b)—(d)分别为AF-Néel,AF-stripy 和AF-zigzag 三种反铁磁态[27]晶胞结构示意图,晶胞中等价的4 个Cr 原子分别用序号1,2,3,4 标注,红色箭头表示Cr 原子的自旋方向.相对于y方向,AF-Néel 型晶胞中1 号和3 号Cr 原子自旋反向(见图1(b)),AF-stripy 型晶胞中1 号和4 号Cr 原子自旋反向(见图1(c)),AF-zigzag 型晶胞中3 号和4 号Cr 原子自旋反向(见图1(d)).

计算的晶格常数a=7.004 Å,与实验值[28]6.95 Å非常接近.单层CrI3是磁性材料[1],如图2所示,通过计算不同应变 (包括沿x方向的锯齿型单轴应变,沿y方向的扶手椅型单轴应变,同时沿x和y方向的双轴应变) 下单层铁磁结构和反铁磁结构的能量差 ΔEFM-AFM发现,施加—8%—8%的单双轴应变后,仅当双轴压缩应变超过6%时,单层CrI3由铁磁态转变为AF-Néel 构型的反铁磁态,其他应变时均保持铁磁态,这与文献[12,29]的报道相符合.

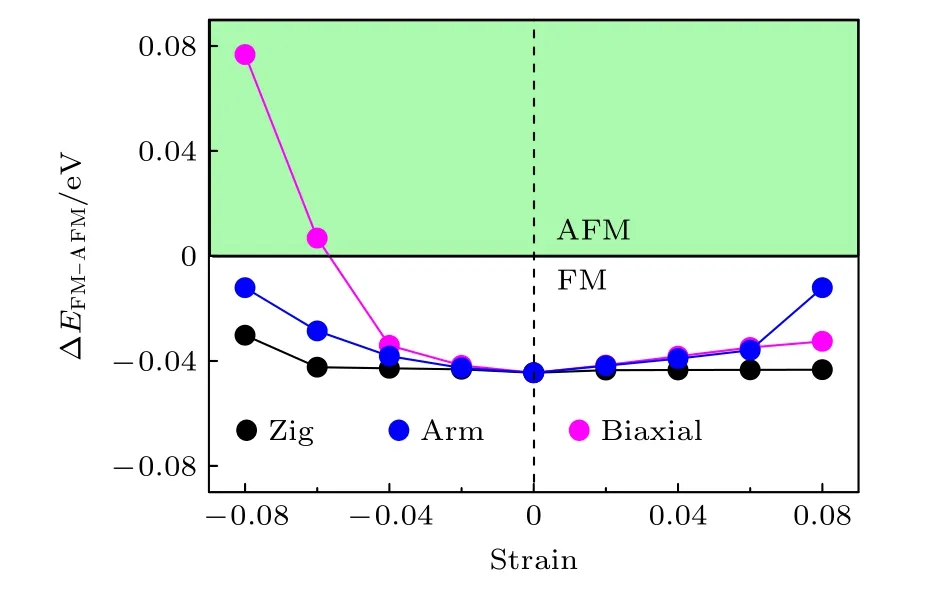
图2 单层CrI3 铁磁结构与反铁磁结构的能量差ΔEFM-AFM随应变的变化规律Fig.2.Variation of energy difference ΔEFM-AFM between single-layer CrI3 ferromagnetic and antiferromagnetic structures with strain.

3.2 电子结构及电学性质

基于3.1 节,利用高精度杂化密度泛函理论HSE06 进一步计算了单层CrI3的电子结构及其电学性质.计算的禁带宽度为2.024 eV,极化向上与极化向下价带顶(valence band maximum,VBM)能级差值 Δ VBM=0.238 eV,极化向下与极化向上导带底(conduction band minimum,CBM)能级差值 Δ CBM=1.592 eV,与文献[16]报道的1.525,0.243,1.609 eV 一致,说明我们后面的计算工作是可信的.与极化向下DOS 相比,极化向上VBM 和CBM 更靠近费米能级(Δ CBM＞0,ΔVBM＞0),体现了CrI3的半半导体属性[16].一方面,如图3(a)所示,施加—8%—8%的双轴应变后,仅当压缩应变超过6%时,有 Δ CBM=0,ΔVBM=0,其他情况ΔCBM,ΔVBM 均大于0,即极化向上与极化向下DOS 不对称,CrI3呈现铁磁性,与3.1 节结论一致;另一方面,如图3(b)所示,这种半导体属性随着单轴拉伸应变量增加而加强,随着压缩应变量增加而减弱,说明单轴应变可以调节单层CrI3的半导体属性.与之同时,通过计算不同应变下的VBM,CBM 和DOS,分析了晶体带隙的变化规律及原因.如图4 所示,三种应变下带隙变化规律一样,均随应变量增大而减小,且压缩应变下较为明显,这是因为CBM 随压缩应变量增大显著下移.

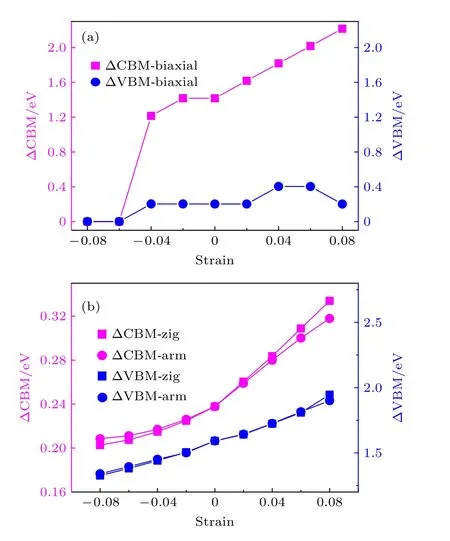
图3 不同应变下的ΔCBM,ΔVBMFig.3.The strain dependence of Δ CBM,ΔVBM.

图4 CBM,VBM 和禁带宽度随应变的变化规律Fig.4.Effect of strain on the CBM,VBM and band gap of CrI3 monolayer.

进一步分析电子DOS 发现,如图5(a1)所示,单层CrI3的VBM 部分主要有I 的3p 态和少量Cr 的3d 态组成,其距离费米能级最近的2 个DOS分布峰分别位于—0.62 eV (极化向上分布峰,1 号峰)和—1.02 eV (极化向下分布峰,2 号峰),距离费米能级最近的导带宽约1.2 eV (由Cr 原子3d 态和I 原子3p 态组成),包含1 个分布峰,位于1.61 eV.显然,电子从价带顶1 号和2 号分布峰跃迁至导带所需要的最低能量均在可见光波段,说明单层CrI3对可见光有较强的吸收本领.当双轴压缩应变量超过6%,如图5(b4),(b5)所示,碘原子间的相互作用增强,VBM 附近出现了新的分布峰 (—6%时位于—0.59 eV,—8%时位于—0.51 eV,3 号峰),处于可见光波段的跃迁能量由原来的2 个变成现在的3 个,电子跃迁变得更容易.

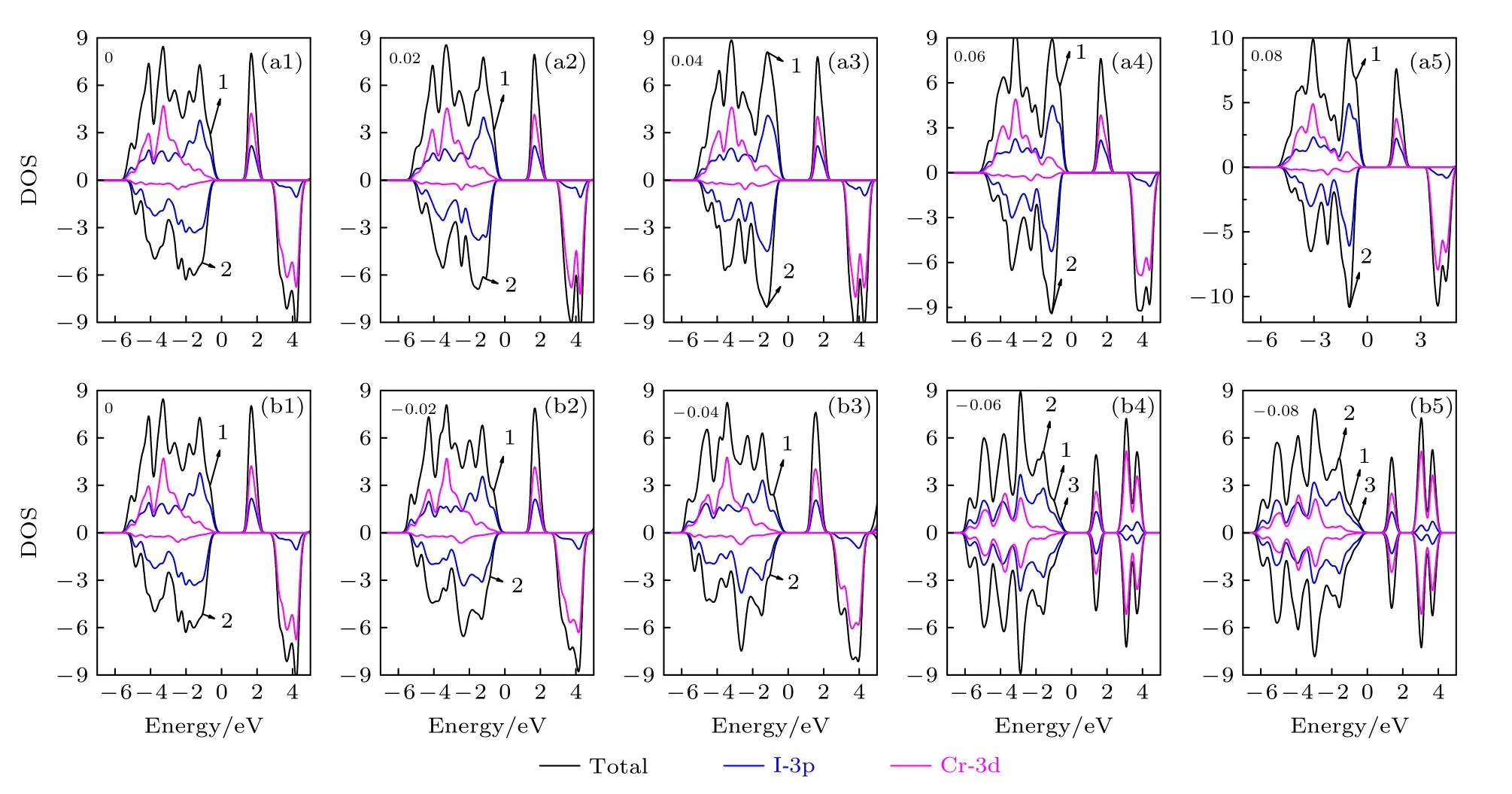
图5 双轴应变下单层CrI3 的电子DOS 分布 (a1)—(a5) 拉伸应变量ε 取0 到0.08;(b1)—(b5) 压缩应变量ε 取0 到—0.08Fig.5.Biaxial strain dependence of DOS of CrI3 monolayer: (a1)—(a5) withεranging from 0 to 0.08 for tensile (compressive) strain;(b1)—(b5) with ε ranging from 0 to —0.08 for compressive strain.

与双轴应变相比,单轴应变下落在可见光波段的跃迁仍然来自于1 号峰和2 号峰,见补充材料图S1 和图S2.与锯齿型单轴应变不同,扶手椅型单轴压缩应变量增至8%时,价带顶附近—0.43 eV位置出现了3 号分布峰,也是因为碘原子3d 态间的杂化程度变强而产生的.

有效质量和迁移率随双轴应变的变化规律见表2 和图6.拉伸应变下,空穴迁移率大于电子迁移率,且随应变量增加而增大,应变量增至8%时空穴迁移率增至原来的2 倍,是因为空穴有效质量随应变量增加而减小,应变量增至8%时空穴有效质量平均减小了28%;电子迁移率和有效质量的变化趋势则刚好相反,应变量增至8%时电子迁移率平均减小了62%,这是因为电子有效质量增至原来的1.6 倍.尽管如此,结果仍不理想,拉伸应变下产生的最大迁移率仅为12.8 cm2·V—1·s—1.

图6 双轴应变下单层CrI3 本征载流子沿x (y)方向的迁移率 (e 代表电子,p 代表空穴)Fig.6.Biaxial strain dependence of the intrinsic carrier mobility of CrI3 monolayer in x (y) direction (e represents for electron,p represents for hole).

表1 单层CrI3 电子和空穴沿x (y)方向的物理参数Table 1.Physical parameters of electron and hole of CrI3 monolayer in x (y) direction,respectively.

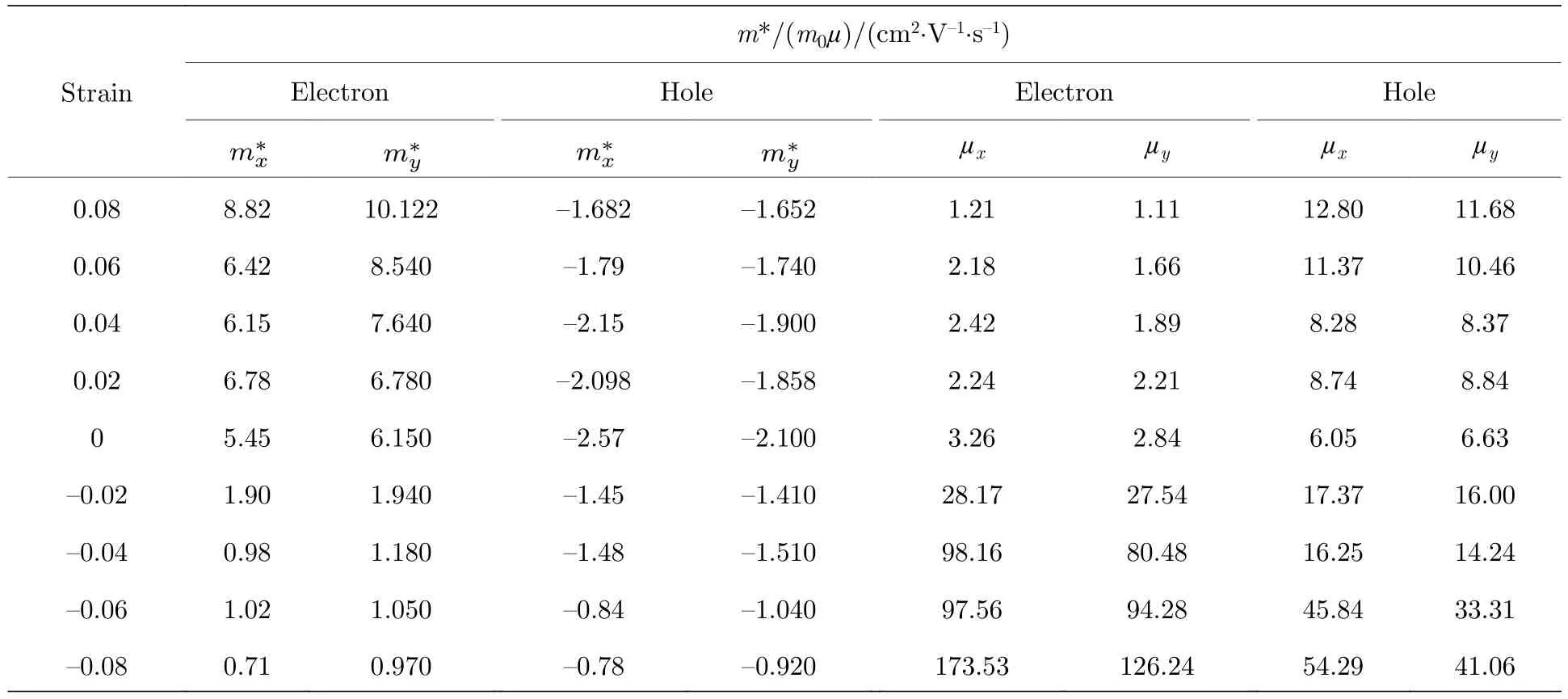
表2 双轴应变下单层CrI3 电子和空穴沿x (y)方向的有效质量m*和迁移率µTable 2.The biaxial strain dependence of the effective mass m* and carrier mobility µ of electron and hole of CrI3 monolayer in x (y) direction,respectively.

与拉伸应变相比,压缩应变下空穴和电子迁移率均随应变量增加而显著增大,其中电子迁移率的增幅大于空穴,是因为应变改变了VBM 和CBM的弥散程度(见补充材料图S3),电子和空穴的有效质量均随应变量增加明显减小,其中电子的减幅大于空穴的,应变量增至8%时,电子和空穴的有效质量分别平均减小到原来的15%和37%,这时沿锯齿方向的电子迁 移率增至174 cm2·V—1·s—1,已达到MoS2[34-36]的水平,说明应变可显著调控单层CrI3的电荷输运性质.

3.3 光学性质

介电函数是表征材料光吸收能力的重要参数[23,36,37].利用高精度杂化密度泛函理论对单层CrI3在可见光范围内的介电函数虚部进行了分析,计算结果如图7 所示,可见光区x(y)方向上有2 个吸收峰,对应光子能量分别为2.51 eV (蓝色光波段,I 号峰)和2.87 eV (紫色光波段,II 号峰),z方向上仅在2.55 eV 处出现1 个吸收峰.一方面,介电函数虚部在不同方向的差异说明单层CrI3具有各向异性的光学性质;另一方面,I 号峰和II 号峰的强度较大说明单层CrI3对可见光有较强的吸收能力,这些与文献[16]报道都一致.材料的电子结构与其光学性质密切相关[38],由3.2 节的DOS结果可知,可见光区介电函数虚部x(y)方向的2 个吸收峰分别来自价带顶附近的2 个分布峰上的电子跃迁.

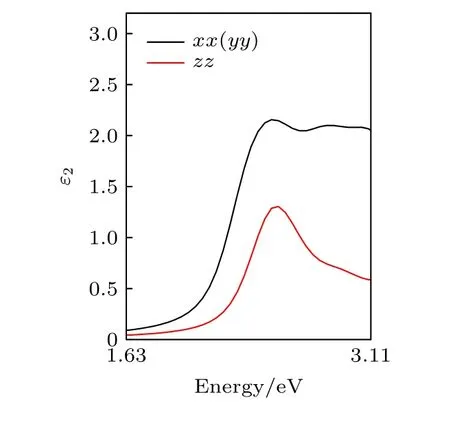
图7 单层CrI3 在可见光区间内的介电函数虚部Fig.7.The imaginary component of dielectric function of CrI3 monolayer in the visible light range.

如图8(a),(c)所示,双轴拉伸应变下,可见光区介电函数虚部x(y)方向上的I 号吸收峰强度随着应变量增加明显增强,当拉伸应变增至8%时,I 号吸收峰红移至绿色光波段 (2.42 eV)且峰值增大了44%.相比之下,z方向变化不明显.双轴压缩应变下,如图8(b),(d) 所示,x(y)和z方向的介电函数虚部曲线开始攀升的起点对应的光子能量随应变量增加明显减小,且可见光区所有吸收峰在应变加大后均往低能量方向移动,这与带隙随应变的变化规律一致,说明压缩应变下电子更容易发生跃迁且材料对可见光的响应得到了明显提升.另外,如图8(b)所示,压缩应变下x(y)方向介电函数虚部的I 号峰强度有所降低,但II 峰显著增强,当应变量增至6%时,介电函数虚部开始出现能量更低的III 号吸收峰 (2.13 eV,黄色光波段),DOS计算结果表明,新的吸收峰是因为I 原子3p 态杂化增强而在价带顶附近出现3 号分布峰上电子跃迁的结果.总之,双轴应变使单层CrI3对可见光的吸收能力变得更强也更容易.

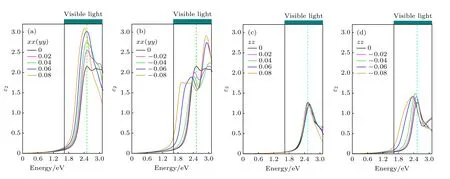
图8 双轴应变下的介电函数虚部 (a),(c) 拉伸应变;(b),(d) 压缩应变Fig.8.Biaxial strain dependence of imaginary component of dielectric function: (a),(c) Tensile strain;(b),(d) compressive strain.

锯齿型和扶手椅型单轴应变下介电函数虚部的变化规律见补充材料图S4 和图S5,与双轴应变相比,单轴应变后单层CrI3对可见光的吸收能力有增强但不明显.

3.4 磁性各向异性

MAE 是表征垂直磁晶各向异性材料的重要参数[39,40].二维六角结构的MAE 满足[41]:MAE=λ1sin2θ+λ2sin4θ,其中λ1,λ2为磁晶各向异性系数,θ为磁化方向与z方向的夹角.如图9 所示,计算发现CrI3原子的磁晶各向异性系数λ1和λ2分别为0.691，0.049 meV/Cr (meV/Cr,表示每个Cr原子的磁性各向异性能),即λ1＞0,λ2＞0,说明单层CrI3具有垂直磁晶各向异性;当θ=90°时,MAE 最大,说明z轴为易轴.除此之外,计算得到MAE=0.7365meV/Cr,与文献[6,7,16]的结论都符合.

图9 单层CrI3 的MAE在y-z 面内的拟合曲线图Fig.9.The curve fitting of MAE in the y-z plane of CrI3 monolayer.

应变是调控低维材料磁性各向异性的重要手段[42,43].对单层CrI3分别施加双轴应变、扶手椅型和锯齿型单轴应变,MAE 的变化规律如图10(a)所示.双轴应变下,MAE 随压缩应变量增加而增大,在—4%应变时增大了32%,随拉伸应变量增加而减小,这与文献[9]结论一致.相比之下,单轴应变有着相似的变化规律,只是变化更为平缓.当扶手椅型或锯齿型压缩应变增大至8%时MAE 分别增大了47%和39%,而拉伸应变8%下MAE 仅仅减小了15%.进一步计算发现,Cr 原子3d 态电子轨道磁矩一致沿着易轴方向,且随着应变呈现与MAE 完全一致的变化规律,如图10(b)所示.

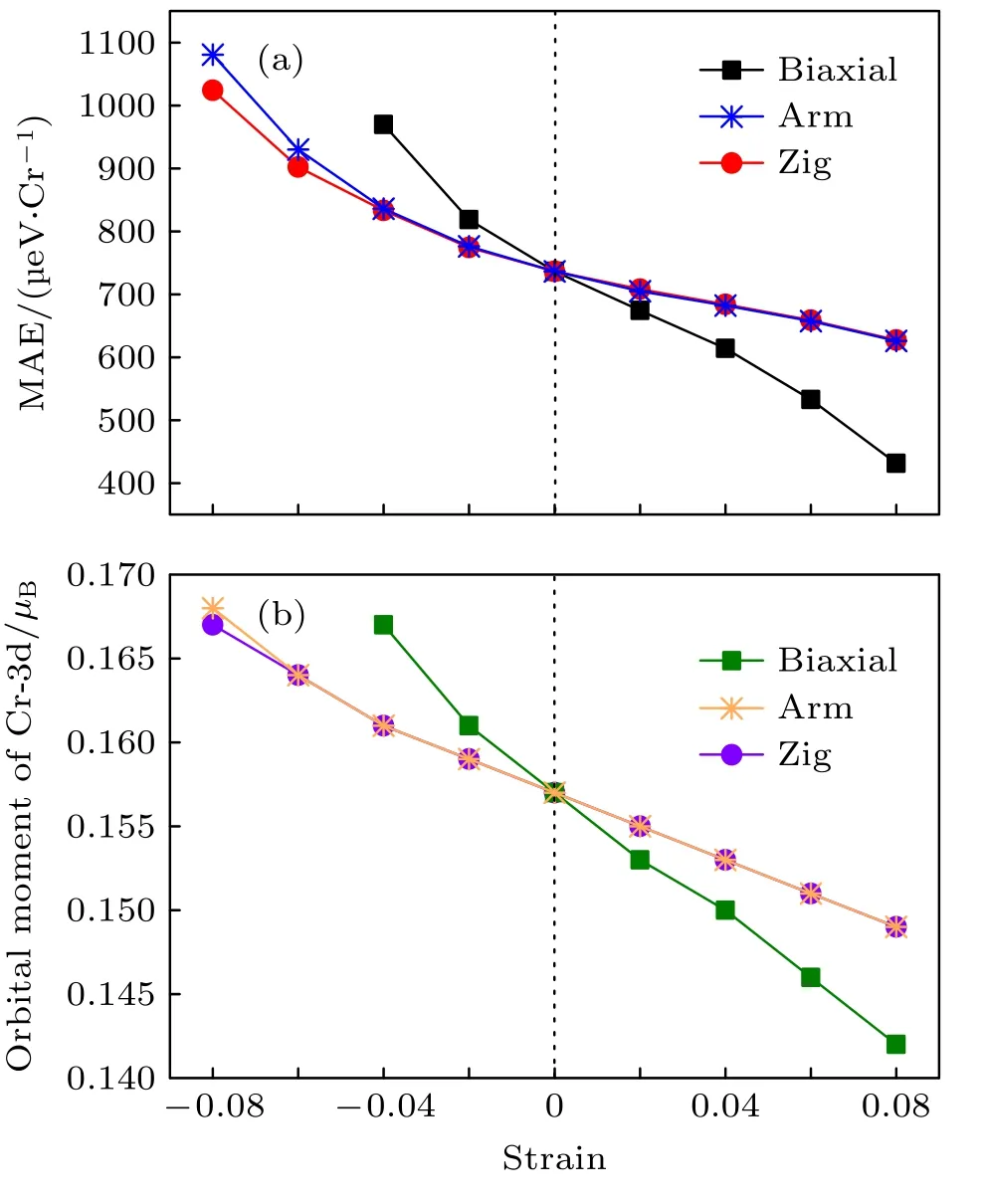
图10 单层CrI3 在不同应变下的MAE (a)和Cr-3d 的轨道磁矩(b)Fig.10.The effect of different strains on the MAE (a) and orbital moments of Cr-3d (b) in CrI3 monolayer.

4 结论

本文采用高精度HSE06 泛函,系统地研究了面内单双轴应变对单层CrI3的电子能带结构、电荷输运性质、可见光区的光吸收性能以及磁晶各向异性的调控规律.计算发现,双轴压缩应变可以明显提升电荷输运性能、可见光区的光吸收能力和磁晶各向异性: 1)当双轴压缩应变量从0 增至8%时,沿锯齿方向的电子迁移率由3 cm2·V—1·s—1增至174 cm2·V—1·s—1;2)可见光区介电函数虚部x(y)方向II 号吸收峰强度随双轴压缩应变量增加明显增强,说明单层CrI3在可见光区光吸收能力增强;3)可见光区介电函数虚部曲线攀升的起点以及吸收峰所对应的能量均随双轴压缩应变量增加发生明显的红移,说明单层CrI3对可见光的响应度增强;4) MAE 随双轴压缩应变量增加而增大,其机理是Cr 原子3d 态电子轨道磁矩一致沿着易轴方向,且随着应变呈现与MAE 完全一致的变化规律.这些研究结果表明,应变调控的确是设计新型二维电子和光电子器件的重要途径.设计一款采用底面晶格常数比单层CrI3小的六方晶体作为衬底材料的应变调控器件,将会大大提升单层CrI3的磁电和磁光性能.