静水条件下垂直圆管负浮力射流的数值模拟
胡玉珊,张仁贡,孙 灿,郑福祥,王 盛,尹则高
(1.浙江同济科技职业学院,浙江 杭州 311231;2.浙江禹贡信息科技有限公司,浙江 杭州 310000;3.中国海洋大学 工程学院,山东 青岛 266100;4.中交疏浚技术装备国家工程研究中心有限公司,上海 201208)
1 研究背景
负浮力射流是自然界和水利工程中常见的复杂水动力现象,例如污水在近海海域的排放。其主要运动特点是射流流体同时受到浮力和初始动量的双重影响,且二者作用方向相反[1-2]。近年来,国内外诸多学者对射流的机理和行为进行了大量分析和研究。理论分析方面,Priestley[3]、Hirst[4]、槐文信等[5]假设高斯流速分布和线性卷吸率,结合整个流场的对称性,研究了静水环境下各种射流的时均特征;Lee等[6]建立了热平流下单孔射流的高斯-涡积分模型,模型预测结果与试验结果吻合较好。物理试验方面,李晶金等[7]利用粒子图像测速技术(particle image velocimetry,PIV)得到了负浮力射流在均匀环境水体下的最大上升高度,并给出了无量纲最大上升高度的表达式;李琼[8]研究了均匀和分层环境流体中负浮力射流的运动规律,揭示了负浮力射流流动行为规律和卷吸特性;Milton-Mcgurk等[9]利用PIV技术和平面激光诱导荧光技术(planner laser induced fluorescence,PLIF)分别观测了射流流体的速度和浓度的沿程衰减过程,发现负浮力射流的卷吸系数小于纯水射流的卷吸系数;Burridge等[10]发现负浮力射流的稳态高度在大尺度涡旋的影响下会发生波动;Abessi等[11]给出了不同倾角下负浮力射流的稀释度公式;张玉玲等[12]采用PIV技术和PLIF技术对波流环境下多孔垂向射流近区的速度场和浓度场进行了测量,对比分析了不同波浪条件下射流运动轨迹、速度场、浓度场及涡量场特性,重点探讨了波流和纯流环境下射流运动特性的差异以及波浪作用对多孔射流发展的影响;丁宏伟等[13]利用PIV技术对静水环境下双孔浮射流的速度场进行了测量,得到了轴线垂向速度的沿程分布。数值模拟方面,李蒙等[14]采用大涡数学模型对横流环境下正弦振荡射流进行了三维模拟,分析了非振荡射流与振荡射流运动特性和稀释规律的差异,并探讨了振荡参数对射流的影响;袁丽蓉[15]建立了静水环境中垂向圆形射流的三维各向异性紊流模型,分析了射流轴线速度和浓度衰减的规律;尹则高等[16]分析了垂直圆管射流流体扩散特征,研究了规则波对负浮力射流三维时均速度以及瞬时浓度的影响,并得到了不同波参数下的中轴线射流垂向速度的沿程衰减规律;张松磊等[17]运用Fluent软件对非静态环境中的负浮力射流进行了模拟和研究,得到了不同时刻的水流流态图以及整个流动过程的流线分布图;Ardalan等[18]开展了静水环境下倾斜射流的数值模拟,发现稀释度与密度弗劳德数的比值可表达为射流初始浮力的二次函数;方神光等[19]对静水中正方形孔口浮力射流特性进行了研究,给出了处于自相似区内射流中轴线上的浓度分布和温度分布;谌霞等[20]建立了三维泥沙和盐度输移扩散的RNGk-ε紊流模型,该模型考虑了泥沙和盐度引起的浮力射流影响,利用该模型对低盐度含沙水流排入某海域后的水力特性以及盐度和含沙量扩散对环境水体的影响进行了模拟预测。
本文建立了静水条件下垂直圆管负浮力射流的三维水动力数学模型和室内物理试验模型,利用物理模型试验观测的垂向速度对数学模型可靠性进行了验证,进而探讨了射流初始速度、初始密度、喷口直径和密度弗劳德数对负浮力射流最大上升高度、稳态高度和中轴线垂向速度的影响,可以为工程应用提供参考依据。
2 三维水动力数学模型
2.1 控制方程
本文基于FLOW-3D软件,利用考虑密度变化的连续性方程、Reynolds时均N-S方程、RNGk-ε湍流模型建立了静水条件下垂直圆管负浮力射流三维水动力数学模型,并利用VOF(volume of fluid)方法进行自由液面的位置捕捉,具体的方程形式可参见文献[16]。
2.2 初始和边界条件
数值模拟在静水水槽内展开,计算开始前设定静水部分水体体积分数为1;水槽底板和边壁均为墙边界条件;基于质量动量法生成负浮力射流源项,具体步骤可参见文献[16],本文不再赘述。
3 物理模型试验及数学模型验证
3.1 物理模型试验
在中国海洋大学长25.0 m、宽1.0 m、高1.2 m的水槽中进行室内物理模型试验,设水槽长为x方向,宽为y方向,高为z方向。试验静水深d=0.6 m,射流喷口距离水槽造波端和底板分别为10.0和0.1 m,喷口内径D=0.015 m,定义射流喷口圆形中心为坐标原点。利用进水管安装的CN-8300型水泵将水箱中密度为ρj=1050 kg/m3的盐水垂直射入密度为ρa=1000 kg/m3的清水中。在进水管上安装流量计进行射流盐水流量监测,同时采用ADV(acoustic Doppler velocimetry)测量典型测点流速。物理模型试验布置如图1所示。
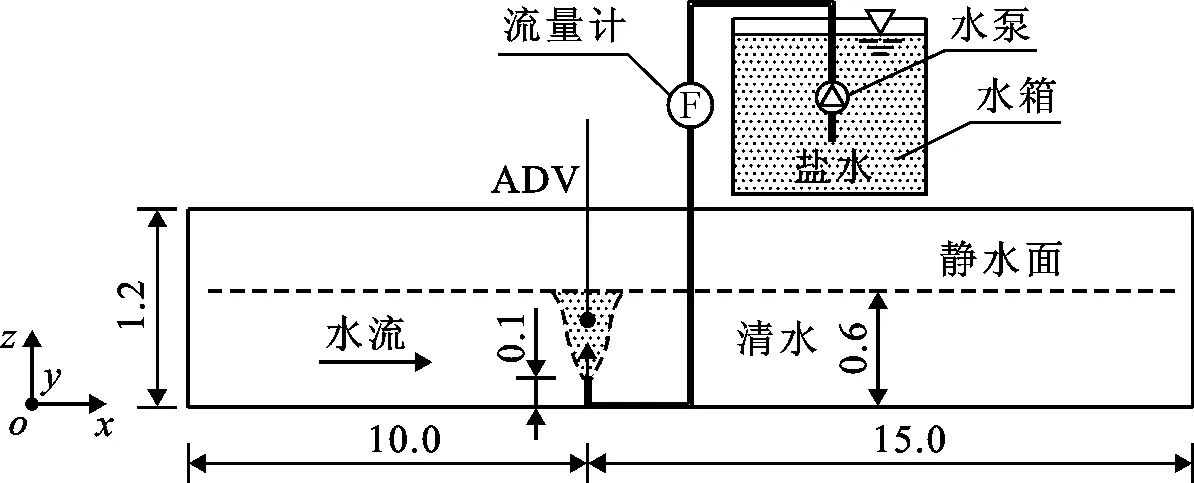
图1 物理模型试验布置示意图(单位:m)
3.2 数学模型验证
图2(a)给出了射流初始速度wj=1.57 m/s,D=0.015 m,ρj=1050 kg/m3工况的无量纲垂向速度w0/wj的验证,其中w0为中轴线上射流垂向速度。图2(b)为距离喷口不同位置剖面水平线上w/w0分布,其中w为流场中某一点的平均垂向速度。由图2可知,数学模型计算结果与物理模型试验数据基本吻合。
4 结果分析与讨论
4.1 数值模拟工况
利用验证后的数学模型,对不同射流初始速度、初始密度和喷口直径下负浮力射流水动力特性进行探究,具体工况见表1,其中静水深d=0.6 m,静止清水密度ρa=1000 kg/m3。
4.2 射流场ρ/ρa值分布
图3给出了射流初始速度wj=1.40 m/s、初始射流密度ρj=1050 kg/m3、射流喷口直径D=0.015 m工况下,不同时刻xoz剖面上流体密度与清水密度的比值ρ/ρa分布。由图3(a)~3(e)可知,射流主体垂直进入环境水体后,不断减速上升到最大上升高度Zm,射流流体在中轴线两侧呈对称分布,以倒锥形向外扩展;整个上升过程中,射流主体边缘和顶部的密度比值不断减小,这是由于射流主体的运动会带动周围水体的运动,促进周围水体与射流流体掺混。到达最大上升高度后,射流顶端流体在负浮力作用下开始下降,但下降动量被黏性效应抑制,在射流上部形成了弥散的云状结构。由图3(f)~3(i)可以发现,重力作用下弥散的云状结构缓慢下降,并与周围水体混合,云状结构逐渐消失。随后,在射流主体两侧形成对称的下降流,射流主体坍塌,射流高度降低并保持到一个稳态高度Zss。其他工况的xoz剖面上射流流体的分布也都有类似的规律,只是在射流初始速度和初始密度不同的工况下,射流主体的最大上升高度和稳态高度不同。

图2 垂直圆管负浮力射流的无量纲垂向速度验证

表1 数值模拟工况表
4.3 射流初始速度wj对w0的影响
图4(a)和4(b)分别给出了不同wj条件下最大上升高度时刻和稳态高度时刻w0的沿程变化,其中ρj=1050 kg/m3,D=0.015 m。由图4(a)可知,当z<0.075 m(5.0D)时,不同工况中轴线上的w0衰减不大,这是由于此区域受射流初始动量的影响较大,浮力影响相对较小,同时射流流体与环境水体之间的黏性效应对w0的衰减影响较小;当z>0.075 m(5.0D)时,射流初始动量的影响减弱,浮力的影响逐渐增强,中轴线上w0衰减趋势加快。由于各工况射流初始密度相同,浮力的影响差别不大,w0衰减趋势也基本一致。随着wj从1.0 m/s增加到1.5 m/s,射流初始动量不断增加,射流最大上升高度由0.31 m增加到0.50 m。图4(b)给出的稳态高度时刻w0沿射流中轴线变化规律与图4(a)相似;喷口断面上的w0数值与wj基本相等;随着远离喷口,稳态高度时刻的w0值显著降低;随着wj由1.0 m/s增加到1.5 m/s,射流的稳态高度由0.19 m增加到0.35 m。
图4(c)和4(d)分别给出了最大上升高度时刻和稳态高度时刻射流中轴线上w0/wj与z/D关系。当z<5.0D时,射流受初始动量的影响较大,数据相对分散,规律性较差;这里只给出了z>5.0D区域内,浮力占主导作用区域内的数据。w0/wj沿z/D的衰减可用下列经验公式来描述:
(1)
式中:B和n为衰减系数和衰减指数。
由图4(c)可以看出,各拟合曲线衰减系数B值介于8.35~9.83之间,n值介于-1.42~-1.25之间,变化幅度相对较小,说明射流初始速度wj对最大上升高度时刻的垂向速度衰减早晚和衰减率的影响有限。与文献[16]得到的B值和平均n值相比,本文最大上升高度时刻的B值较小,n值较大,说明静水条件下垂直圆管负浮力射流中轴线上垂向速度衰减较早,衰减率较小。由图4(d)可以看出,随着wj从1.0 m/s增加到1.5 m/s,拟合曲线的B值从25.86减小至7.95,n值则从-2.15增大至-1.23,说明稳态高度时刻射流中轴线上垂向速度衰减较早,衰减率减小。图4(c)和4(d)给出的n值均小于文献[21]给出规则波工况下纯水射流的n值-1.07,说明稳态高度时刻射流中轴上垂向速度的衰减率大于规则波作用下纯水射流的对应值。
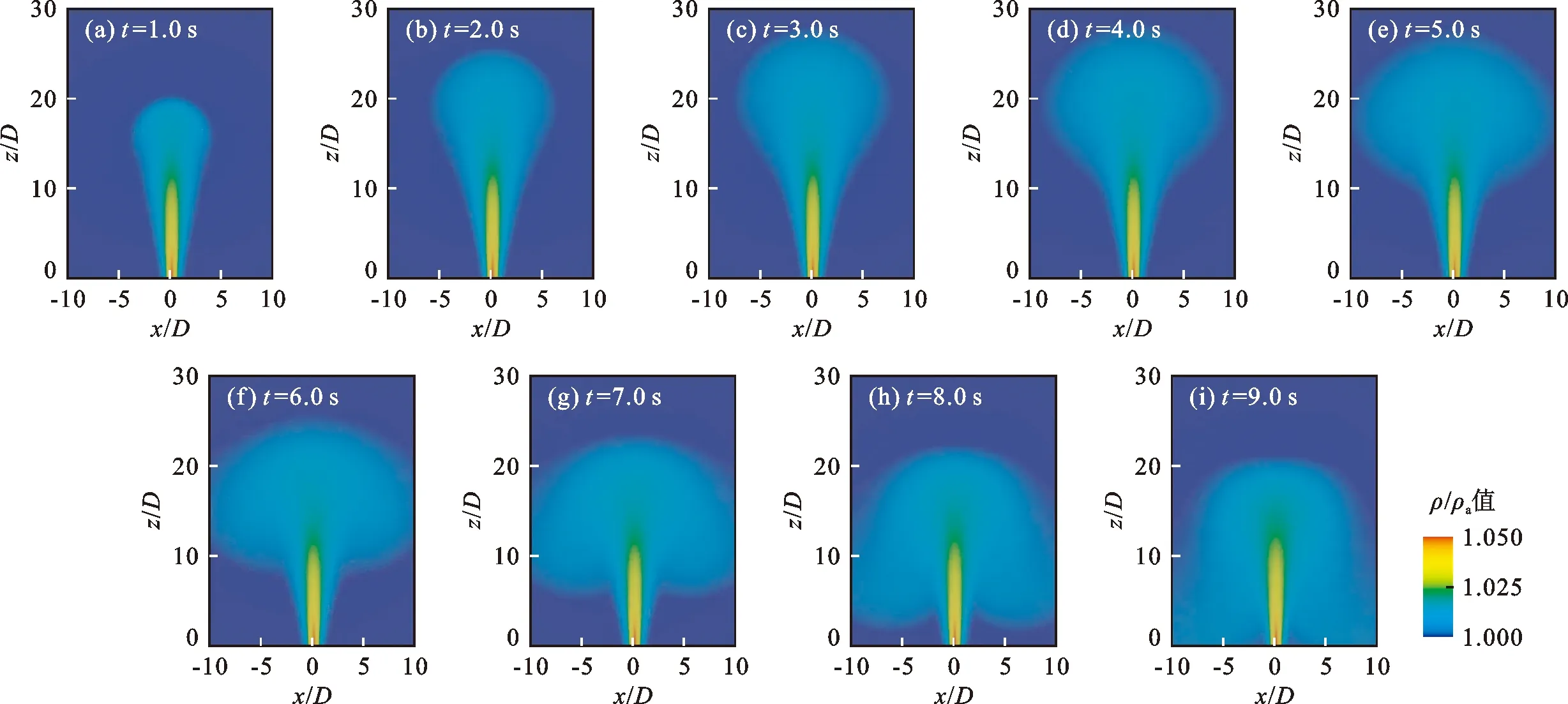
图3 xoz剖面上不同时刻流体密度与清水密度比值ρ/ρa分布(ρj=1050 kg/m3,wj=1.40 m/s,D=0.015 m)
4.4 射流初始密度ρj对w0的影响
图5(a)和5(b)分别给出了不同ρj条件下最大上升高度时刻和稳态高度时刻w0的沿程变化,其中wj=1.30 m/s,D=0.015 m。由图5(a)可知,射流到达最大上升高度时刻,w0沿程分布可近似分为3段:z<0.075 m(5.0D)时,射流初始动量作用较大,浮力作用相对较小,不同工况中轴线上w0衰减趋势均较缓;0.075 m(5.0D)
图5(c)和5(d)分别给出了z>5.0D范围内最大上升高度时刻和稳态高度时刻射流中轴线上w0/wj与z/D关系。由图5(c)可以看出,各拟合曲线衰减系数B值介于7.57~8.88之间,n值介于-1.29~-1.19之间,变化幅度相对较小,说明射流初始密度ρj对最大上升高度时刻的垂向速度衰减早晚和衰减率的影响不大。由图5(d)可以看出,随着ρj从1 030 kg/m3增加到1 070 kg/m3,稳态高度时刻拟合曲线的B值从7.79增加到16.84,n值则从-1.21减小到-1.77,说明此时射流中轴线上垂向速度衰减较晚,衰减率增加。与文献[16]得到的平均n值相比,本文最大上升高度时刻和稳态高度时刻的n值均较大,说明静水条件下垂直圆管负浮力射流中轴线上垂向速度衰减率较小。
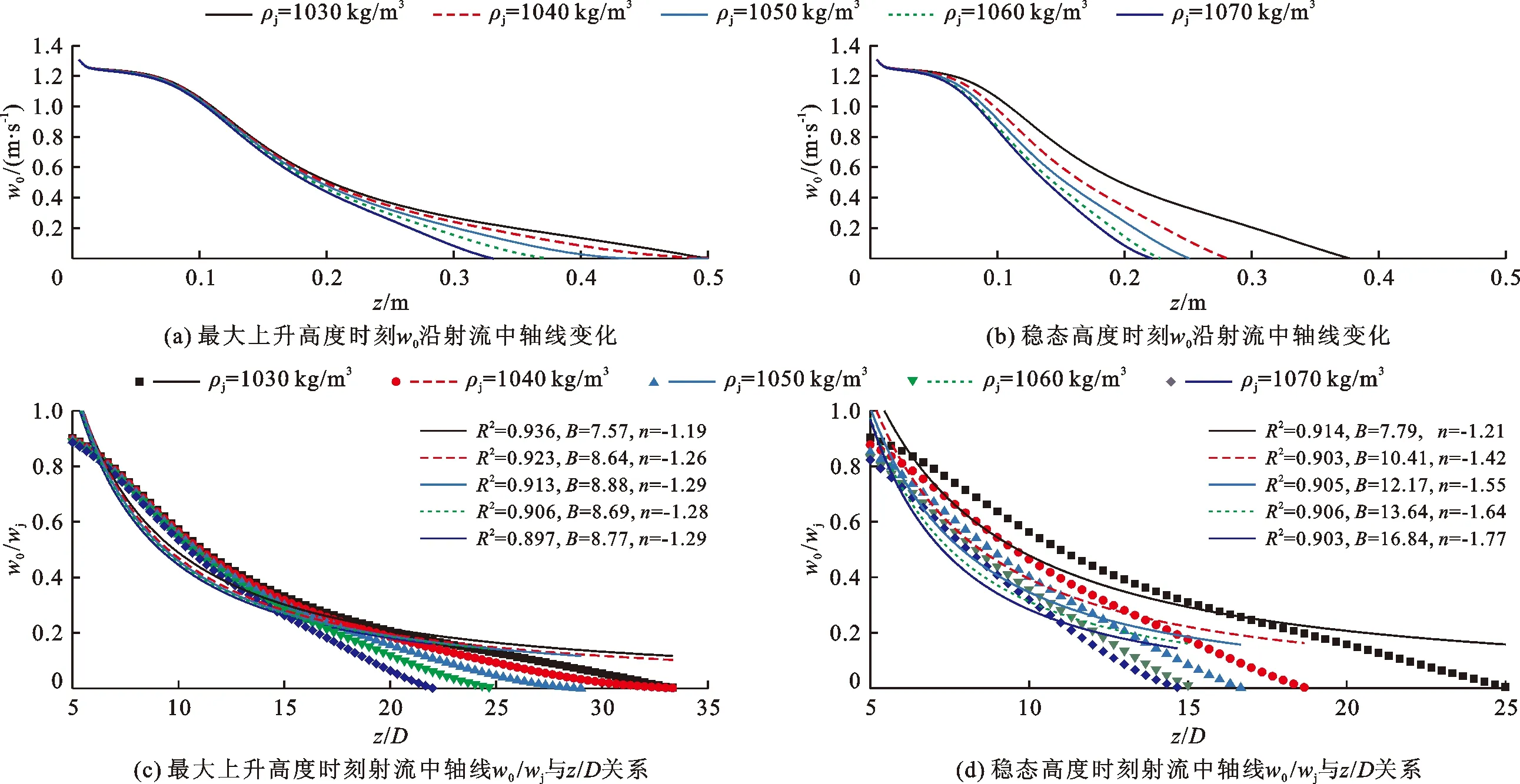
图5 不同ρj条件下射流中轴线上垂向速度w0沿程变化(wj=1.30 m/s,D=0.015 m)
4.5 射流喷口直径D对w0的影响
图6(a)和6(b)分别给出了不同喷口直径D条件下最大上升高度时刻和稳态高度时刻w0的沿程变化,其中ρj=1050 kg/m3,且射流流量保持恒定,均为0.277 L/s。由图6(a)和6(b)可知,随着喷口直径D的增加,射流中轴线上w0相应减小。随着喷口直径D由0.014 m增加到0.016 m,射流最大上升高度由0.50 m降低至0.42 m,射流稳态高度由0.50 m降低至0.25 m。
图6(c)和6(d)分别给出了z>5.0D范围内最大上升高度时刻和稳态高度时刻射流中轴线上w0/wj与z/D关系。由图6(c)和6(d)可知,随着D从0.016 m减小至0.014 m,最大上升高度时刻拟合曲线的B值从8.76降低到6.27,n值则从-1.29增加到-1.07;稳态高度时刻拟合曲线的B值从14.36降低到7.32,n值则从-1.61增加到-1.12,即衰减较早,衰减率减小。与文献[16]得到的平均n值相比,本文最大上升高度时刻和稳态高度时刻的n值均较大,说明静水条件下垂直圆管负浮力射流中轴线上垂向速度衰减率较小。
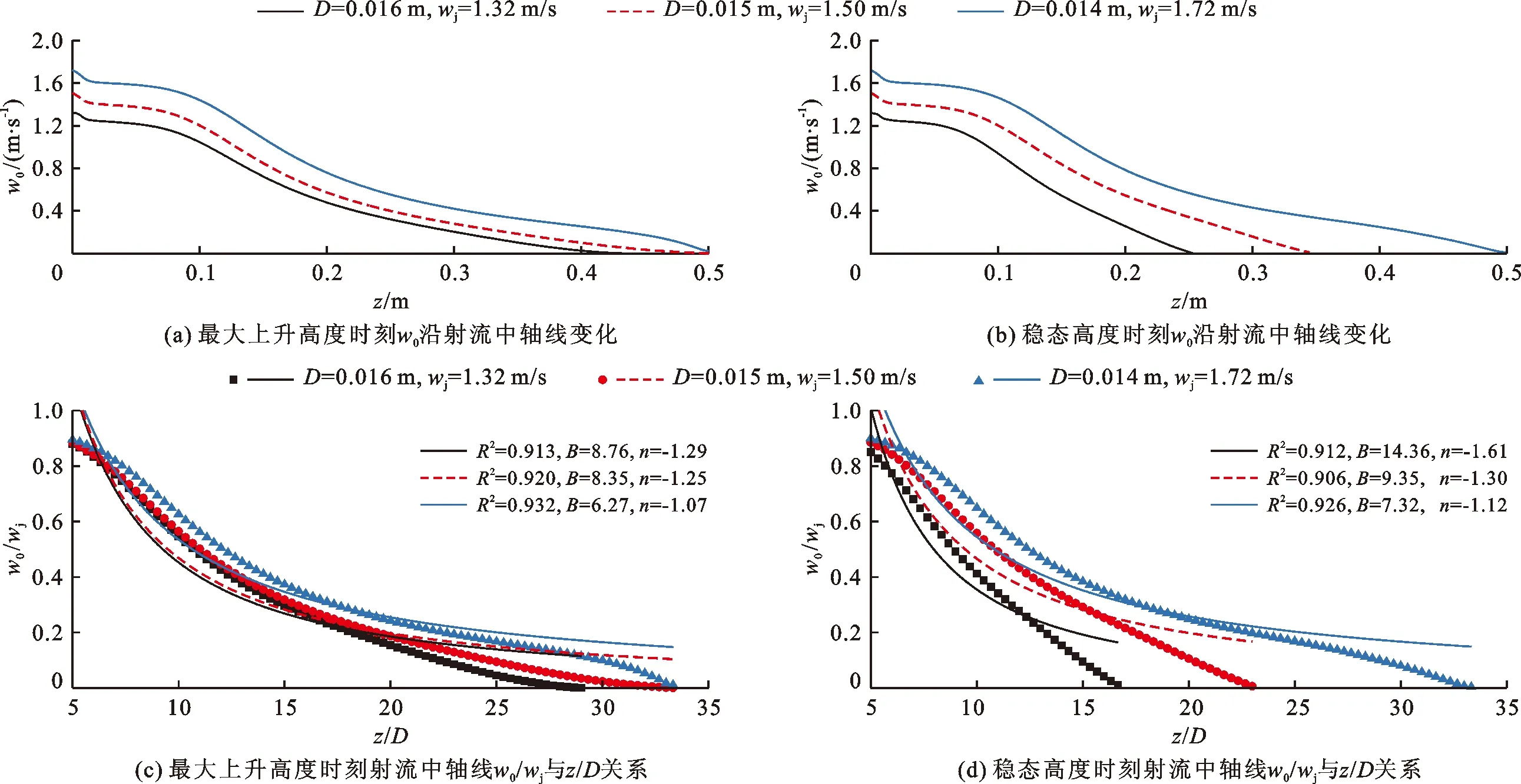
图6 不同D条件下射流中轴线上w0沿程变化(ρj=1050 kg/m3)
4.6 密度弗劳德数的影响
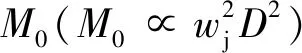
Zm∝M03/4/B01/2∝D1/2wj/(g′)1/2=D·Fr
(2)
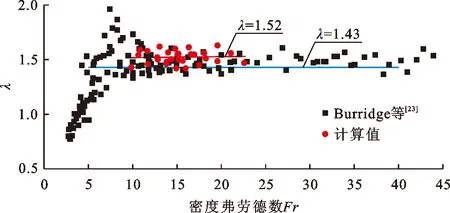
图7给出了射流无量纲最大上升高度Zm/D和无量纲稳态高度Zss/D与密度弗劳德数Fr的关系以及拟合直线,其中Zm和Zss分别为射流最大上升高度和稳态高度。由图7可以看出,在本文密度弗劳德数研究范围内(10 图8为射流最大上升高度与稳态高度的比值λ(λ=Zm/Zss)与密度弗劳德数Fr的关系。由图8可知,λ与Fr基本无关。图8中方形点为Burridge等[10]给出0.4≤Fr≤45范围内的试验数据,其拟合直线表达式为λ=1.43,与密度弗劳德数Fr无关。圆形点为10≤Fr≤23范围内本研究的数值计算值,对其进行拟合得到λ=1.52,略大于Burridge等[10]给出的λ=1.43。原因是由于Fr<6.5范围内,Burridge等[10]给出的λ值很大一部分小于1而引起的。 图7 无量纲最大上升高度Zm/D及稳态高度Zss/D与密度弗劳德数Fr的关系 图8 最大上升高度与稳态高度比值λ与密度弗劳德数Fr关系 基于数值模拟等方法,对静水条件下垂直圆管负浮力射流特性进行研究,得到以下结论: (1)随着射流初始速度的增加,射流初始密度的降低和喷口直径的减小,射流最大上升高度和稳态高度均增加。 (2)静水条件下,射流初始速度和射流初始密度对最大上升高度时刻的中轴线垂向速度衰减早晚和衰减率的影响不大;随着射流初始密度的增加,稳态高度时刻的射流中轴线上垂向速度衰减较晚,衰减率增加;垂直圆管负浮力射流量一定时,随着喷口直径的增加,最大上升高度时刻和稳态高度时刻射流中轴线上垂向流速衰减较早,衰减率减小。与规则波作用下的垂直圆管负浮力射流相比,本研究中最大上升高度时刻射流中轴线上垂向速度衰减较早,衰减率也较小;与规则波工况下的纯水射流相比,本研究中稳态高度时刻射流中轴上垂向速度衰减率相对较大。 (3)建立了密度弗劳德数表达的无量纲最大上升高度和稳态高度线性关系式;发现本研究中射流最大上升高度和稳态高度比值趋近于常数1.52,与密度弗劳德数基本无关。需要指出的是,为研究方便,本文静水深均取0.6 m,导致喷口直径较小和射流初始速度工况下的最大上升高度和稳态高度基本相等,未出现较大静水深条件下前者大于后者的现象。因此,下一步需要深入研究不同水深对负浮力射流上升高度的复杂影响,并阐明其影响规律。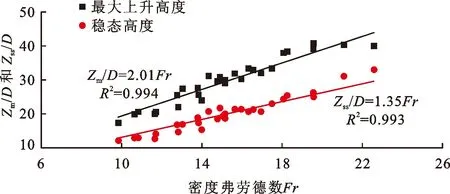
5 结 论

