FPGA在人工智能深度学习中的应用

武汉工程大学邮电与信息工程学院 周莹

近年来，FPGA应用的呼声之高，发展之快令人振奋，从AI到VR，从语音识别，人脸识别到各种各样的加速器。在人工智能兴起和发展的时代，深度学习起到了中流砥柱的作用，然而深度学习仍然面临着超大计算量的问题，GPU、ASIC、FPGA都是解决庞大计算量的有效方案。本文将以Lenet卷积神经网络模型为例，基于CNN网络模型和硬件架构实现，对CNN网络的后向训练过程进行Matlab定点仿真和FPGA实现以及Modelsim仿真验证，最终综合对比FPGA、GPU、CPU的性能。

人工智能是研究用于模拟和扩展人类行为的一门新型技术学科。对于人工智能，特别是基于深度学习的应用来说，很多应用场所都对实时性有着很高的要求[1]。面对这个新时代提出的新要求，FPGA利用其特点，发挥着它重要的作用[2]。下文以CNN网络的后向训练过程为例说明FPGA的性能优势。

DNN（深层神经网络）包含两类核心算法：CNN（卷积神经网络）和LSTM（长短期记忆网络），都能在很大程度上受益于低精度的乘加运算[3]。CNN算法目前是最重要的深度学习方法之一，这种算法在图像识别以及语音识别应用中取得了突破性的成就，下面就以CNN算法的后向训练过程模型架构及结果仿真为例，说明FPGA在深度学习算法加速上的优势。

1 CNN的网络模型

下面以一种具体的Lenet卷积神经网络模型为例，给该CNN一个输入，输入名为MINST的一个数据集，也就是一张灰度图像，其像素是（1,28,28），如图1所示。

其conv1作为第一个卷积层，卷积核的大小是（4,1,5,5），其中的4代表有4个（1,5,5）的卷积；利用非全零的方法进行填充，步长取1，Relu作为其激活函数，再依据（式1）和（式2）可得，输出（4,24,24）；第1个池化层是Pooling1，经过这个池化层之后，再采用最大池化策略的方式，利用非全零的方法进行填充，步长取2，这时的输出是（4,12,12）；conv2作为第二个卷积层，它的conv2卷积核大小是（4,4,5,5,），其中的4是指有4个（4,5,5）卷积，利用非全零填充的方法进行填充，步长取1，Relu作为其激活函数，根据（式1）和（式2）可得，经过卷积后的输出是（4,8,8）；接着进入到第二个池化层pooling2，采用Max Pooling的方式且池化值为（2,2），最终的输出为（4,4,4）；经过2层全连接层FC1和FC2，FC1的大小是（12,64），激活函数是Relu，FC2的大小是（10,12），激活函数是Softmax。

通过该模型的训练之后，可以得到如图2所示的系统损失函数的变化曲线，随着迭代次数的叠加，损失函数将会逐渐变小，在开始的四千次迭代中损失函数的变化是迅速变小，而之后的四千到八千次时，曲线已经变得非常缓慢，直到最后趋于平稳。

可以通过曲线图发现：随着迭代次数的增加，损失函数逐渐减小，最终会趋向一个稳定值；而准确率的曲线图是会不断增大，最终也趋向于一个稳定值，准确率曲线图此处略[4]。总之，这种模型的损失函数变化曲线和准确率变化曲线都符合要求，性能良好。下文以该模型为例，介绍硬件加速的实现。

2 CNN的硬件结构

对于CNN的后向训练过程，包含全连接层、池化层传递过程以及卷积层误差；同时也包括了权值的更新。CNN硬件框架是以后向训练过程的误差传递过程为主，前向预测过程的输出结果长度为10，作为结构的输入，通过和Label（正确标签）相减取得差值之后，便得到了全连接层FullConnected2的误差项，再经过全连接层隐层的误差传递，会得到全连接层FullConnected1的误差项，最终得到有效长度是8的4路卷积层，最后经过池化层的误差项传递和卷积层误差项传递，就会得到有效长度为24的4路卷积层[5]。参数更新模块被进入的误差项进行更新之后，权值和偏置项也会被更新。下面介绍利用FPGA实现全连接层后向过程的仿真验证。

3 FPGA实现全连接层后向过程仿真验证

3.1 Matlab定点仿真

（1）根据卷积神经网络训练的算法理论，对上述Lenet卷积神经网络的后向训练过程进行Matlab的定点仿真。在Matlab中进行仿真，首先将数据集中的“mnist.train.images.txt”文件输入，把“mnist.train.labels.txt”当做正确标志。均值设为0.1，初始化权值使用0，初始化方式采用标准差。

（2）向训练过程的定点方式采用1位符号位、5位整数位、12位小数位，即FI（1,18,12），采用这种方式后的输出数据是卷积层为1的偏置b_conv1和权值w_conv1，卷积层为2的偏置b_conv2和权值w_conv2，全连接层为1的偏置b_full_connected1和权值w_full_connected1，全连接层为2的偏置b_full_connected2和权值w_full_connected2[6]。如图3所示，训练的迭代次数是横坐标，数据的最大相对误差值是纵坐标，经过分析训练过程中的相对误差绝对值，可以得到相对误差的最大值是10∧-2，显然这个误差结果是在期望值中的。

3.2 FPGA实现和结果验证

Lenet卷积神经网络中全连接层隐层的误差传递过程的Modelsim仿真结果如图4所示，模块是以10个连续误差数据作为输入，输出是12路并行误差数据，该数据是由有效控制模块和12个乘累加器得到的，利用Matlab仿真的结果与这个结果一样，意味着模块正确。

其中，全连接层隐层误差传递模块的端口信号定义如表1所示。

表1 模块的端口信号说明-误差传递Tab.1 Module's port signal description - error propagation

Lenet卷积神经网络中全连接层隐层的权值更新过程由第三方仿真工具Modelsim得出的时序结果如图5所示，该模块的输入是单个的误差数据，输出是64位的1路数据，即64个权值。一个误差更新64个权值，因此12个误差更新了所有的768个权值[7]。Matlab仿真结果和FPGA经过第三方仿真工具Modelsim的结果一样，意味着模块功能正确。

其中，全连接层隐层权值更新过程的端口信号定义如表2所示。

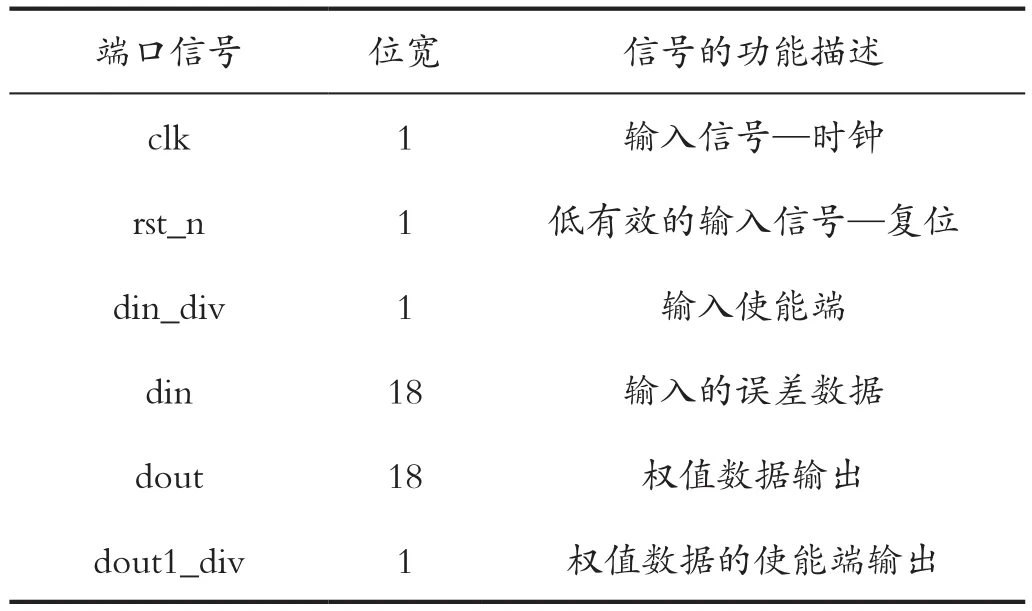
表2 端口信号说明-权值更新Tab.2 Port signal description - weight update

实现卷积神经网络后向训练过程之后，经过Modelsim仿真的波形图如图6所示。由时序图可得，在FPGA中只要实现了一次后向训练，就需要821个时钟信号，由于最大CLK频率设定为200MHz，即5NS[8]。

通过分析后向训练在FPGA、GPU、CPU的性能，如表3所示。FPGA实现的后向训练过程对比CPU来说，处理速度提高了1.8倍，由于该结果受到训练过程中一系列外在因素的影响，例如权重相对正向过程需要转置，就会浪费一定的处理时间[9]。虽然FPGA相对于GPU，处理速度稍有差距。但是FPGA功耗比GPU和CPU要小很多。

表3 后向训练过程FPGA、GPU、CPU性能对比Tab.3 Backward training process FPGA, GPU, CPU performance comparison

4 结语

目前深度学习的流行，其实仍然是得益于大数据和计算性能的提升。但是却也遭受着计算能力和数据量限制的瓶颈。针对数据量的需求，还能够利用调整或者变更模型来缓解，但面对计算力的挑战，却没有捷径。FPGA解决了传统PLD资源有限的劣势，又克服了全定制的电路较死板的缺点[10]。随着FPGA器件和云端部署等技术的发展，内存带宽已经逐渐不再是DNN的算力瓶颈，取而代之的是单周期可以完成的乘加操作数量，这些都使得FPGA在未来的AI领域中，能够发挥它最大的优势，推动科技的进步。