Analytical model for Rayleigh–Taylor instability in conical target conduction region

Zhong-Yuan Zhu(朱仲源) Yun-Xing Liu(刘云星) Ying-Jun Li(李英骏) and Jie Zhang(张杰)

1School of Science,China University of Mining and Technology,Beijing 100083,China

2Double-cone Ignition(DCI)Joint Team,State Key Laboratory for Geomechanics and Deep Underground Engineering,China University of Mining and Technology,Beijing 100083,China

3Double-cone Ignition(DCI)Joint Team,Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

Keywords: double-cone ignition,Rayleigh–Taylor instability,conical target conduction region

1. Introduction

In inertial confinement fusion (ICF)[1–10]schemes with directly driven conical and spherical targets, the Rayleigh–Taylor instability (RTI) imposes a fundamental constraint on the design parameters required for both of these ignition schemes.[11–14]Livescuet al.[15–17]studied RTI using direct numerical simulations. Yu and Ye[18]also adopted numerical simulations of hydrodynamic instabilities during direct-drive ICF implosion ignition based on the LARED-S program, but these were for the spherical target. In 1986, a formalism for the semi-analytical form of RTI in spherical geometry was developed by Gupta and Lawand.[19]In 1996, Sanz proposed a self-consistent analytical model for RTI in ICF.[20]Most of the works mentioned above are restricted to numerical simulations or only aim to study RTI in direct-drive spherical targets.In 2020, Zhang proposed a new ignition scheme,[21]i.e., the double-cone ignition scheme (Fig. 1). It is well known that during the direct drive of a spherical target pellet,the ablation front is unstable,affecting the central implosion ignition of the pellet. However,what is actually affected by RTI during laserirradiated conical targets is the compression process.[22,23]In 2022, Fang and Zhanget al.[24]conducted experimental and numerical simulations to study RTI in conical targets caused by factors such as the thickness of the target pellet, but their work ignored the effect of laser-plasma instability(LPI).

Studies have been carried out on the heat conduction region. De Groot[25]proposed an analytical model of a planar plasma in 1992, which explicitly includes the temporal evolution of the heat conduction region. Models for the onedimensional resolution of the plasma in the conduction region in a planar target have been given by Chang and Li,[26–28]respectively. In 2020, Bettiet al.[29]also presented a semianalytical model of the hot spot and compressible shell,using analytical and simulation methods to study the physics of burn propagation in inertially confined plasmas. In Refs. [30–32],the parameters of the heat conduction region in the planar target have also been investigated experimentally[30]and numerically[31,32]by numerous researchers. Notably,in order to better analyze and solve the RTI of the compression process,the authors developed an analytical model of the plasma in the conduction zone instead of modeling the hydrodynamic instability of the ablation surface. Moreover, for the purpose of this paper, the parameters of the plasma (length, density,temperature,etc.) in the conduction zone are given below.

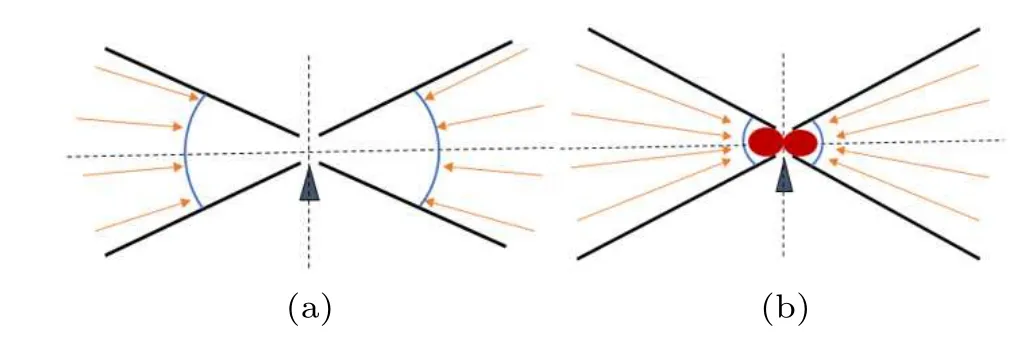
Fig.1. (a)Schematic of the initial stage. The yellow line in this diagram is the drive laser;the two sides are composed of symmetrical metal walls;and the ignition assembly is placed in the center of the entire unit. (b)Schematic of the compression stage. As the compressed fuel is ejected at high speed and fused together,the ignition assembly ignites and triggers fusion.[33]

The authors ignored the viscosity between the two metal walls and the fusion fuel. The incompressibility(i.e.,isobaric approximation) has been widely used in the analytical treatment of the ablation RTI at the ablation front over the past decades. The formula for the growth rate of RTI[34–36]at the ablation front in ICF is expressed as follows:

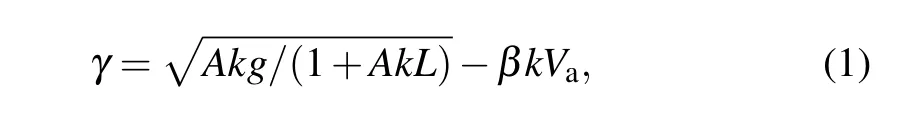
wherekis the perturbed wave number; Atwood numberA=(ρ2-ρ1)/(ρ2+ρ1),gis the acceleration;Vais the ablation velocity;β ≈2–4 is expected in the direct-drive ablation;andLis the thickness of the fluid density layer. In combination with the specific parameters of the plasma obtained through the analytical model developed in this paper,it is necessary to analyze the RTI of the compression process in a conical target.This is the reason for and significance of the model described in this paper,and the analytical results are more intuitive than the numerical solutions.

2. Analytical model and application

Since the laser is uniformly irradiated on the spherical target,the polarization angle of the laser irradiation is 2π. However, in the conical target model, the angle becomes smaller compared to that of the former. The authors temporarily define this angle asθ,which ranges from 90°to 120°. Namely,the current study in this paper is two-dimensional(2D).

In Ref. [26], Li gave a one-dimensional self-similar model based on the hydrodynamic behavior of a flat target.Based on research by previous scholars,this paper introduces the physical process of the conduction region in the direct driven conical target model(Fig.2),focusing on the fluid behavior and properties exhibited by the plasma in the conduction region.

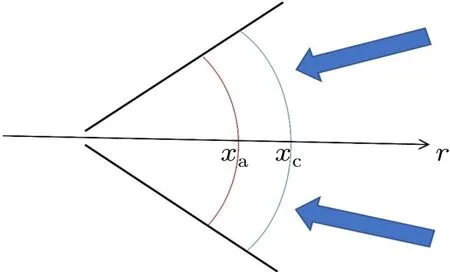
Fig. 2. Diagram of conical target conduction region. The authors define xa as the ablation surface and xc as the critical density surface. In addition,xc is the coordinate origin.

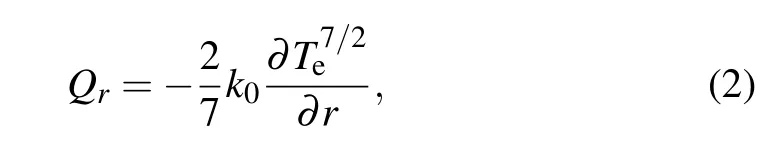
When laser irradiates a solid target to generate plasma,the whole region is usually divided into three regions,[37,38]i.e.,the compression region,conduction region and corona region.The boundary between the conduction and corona regions is the critical density surface. The generation of the plasma conduction region of the laser-irradiated conical target consists of three steps. First,the laser acts on the critical density surface of plasma on the conical target,and is absorbed mainly in the corona region since it cannot enter the critical density surface.Plasma heats the conduction region via electron heat conduction. In the 2D case,the electron heat conduction model[39,40]is expressed as whereQris heat flux;Teis electron temperature;and the heat flux isQ=-κ∂Te/∂r, whereκis thermal conductivity andκ∝T5/2e. Therefore,the heat energy entering the conduction region through electron heat conduction is the main energy source for plasma generation. Second, the plasma generated by the ablation of the solid material flows away from the ablation surface.The mass of a conical target ablated in unit time is called an ablation rate and is represented by dm/dt.Third,the authors consider that the driving laser is a long pulse,the conduction region reaches a steady state, and the fluid behavior in the conduction region is steady. The electron heat conduction increases the temperature in the conduction region,while the ablation decreases the temperature and increases the density. The expansion of the plasma results in decreases in its temperature and density. Many factors cause the plasma in the conduction region to expand isobarically. Therefore, the authors adopted an isobaric assumption in this model.

Considering that the authors mainly study the conduction region with electron densityne＞ncaway from the target in space,it is heat conduction,expansion,ablation,and other factors in this region that lead to its equilibrium state. Therefore,plasma fluids can be seen as quasi-steady. As the laser is completely absorbed in the corona region, in the heat conduction region,Te≫Ti,P ≈Pe, andQ ≈Qe(Teis the temperature of electrons;Tiis the temperature of ions;Peis the pressure of electrons; andQeis the electronic heat flux). At the same time, assuming that the laser irradiation uniformity is good,the authors consider that the fluid behavior in the conduction region conforms to the steady-state assumption. Then,the expression for the single-fluid,steady-state,and viscous-free hydrodynamic equations are as follows:

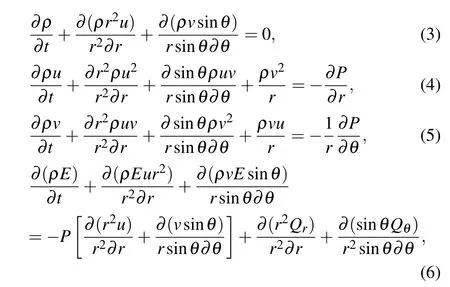
whereρ,P, andu(v) are the density, pressure, and velocity,respectively, of the plasma;E=ε+(u2/2);εis the internal energy per unit mass;andQis the heat flux.

In order to facilitate the use of the analysis results of the self-similar equation,the authors adopted convenient units,as shown in Table 1.

Table 1. Normalized values for scaled variables.

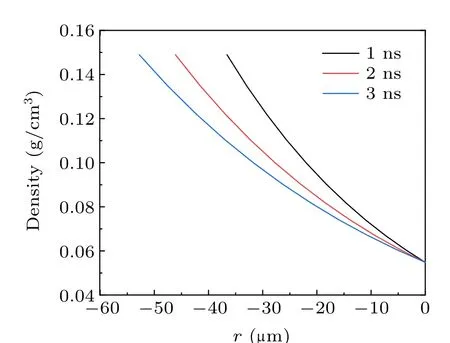
Fig. 3. Evolution of density of plasma as a function of the spatial location for different pulse widths. Laser pulse widths of 1 ns, 2 ns, and 3 ns were randomly selected. Driving laser power density I=3.0×1014 W/cm2.

Due to Eq. (4) and the ideal gas condition, the authors consider the pressure formulaP=ρC2sin Ref. [25], and the pressure in the conduction region is constant atPc,

Solution(11)for the density shows that the length of the plasma and the angleθof the conical target can affect the changing pattern of the density. Whenθis kept constant,the longer the length of the plasma, the slower the density decreases; whereas, whenLris kept constant, the larger theθ,the steeper the density decrease trend of the plasma in the conduction zone. Figure 3 shows that when the pulse time or laser intensity is properly enhanced, the width of the conduction zone becomes larger and the density of the plasma decreases slowly, which is favorable for reducing the effects caused by RTI.

The pulsed laser energy is absorbed in the corona region and cannot enter the conduction region. According to the work of De Grootet al.,[42,43]ρu= dm/dt, which is the ablation rate equation. From Eq. (6) and the pressure equation, the authors obtainC2s˙m(1+(u2/2C2s))=-Qr. It is known thatE=ε+(1/2)u2andε= (3/2)meC2s, whileme=9.1×10-31g, which is so small that it can be ignored.The plasma fluid velocity in the conduction region is less than the velocity of sonic surface,which leads to 0≤(u2/C2s)≤1,resulting in at the same time, the authors focus on the boundary condition of the conduction region. Whenr=0,T ≈Tc(whereTcis the temperature of the corona region). Additionally, whenr=-Lr,T ≈0. Therefore,the solution for temperature is and since the origin of the coordinates is on the critical density surface,the value ofris considered to be in the range[-Lr,0].Then, the following results are obtained using the coordinate transformation of Eq.(19):where the value range ofr(cm)is[-Lr,0]and the value range ofθis between 90°and 120°. Equations (2) and (22) show that,when the driving laser intensity and pulse time are guaranteed to be constant, the larger the angleθ, the higher the temperature near the coronal region. Similarly,if the angleθis held constant,increasing the intensity of the drive laser will also lead to a higher temperature near the coronal region,i.e.,the temperature trend in the conduction zone will also become steeper.

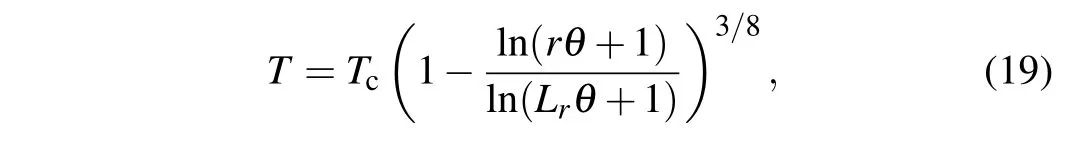
Since the authors only consider the plasma length between the critical density surface (coordinate origin) and the ablation surface, based on the physical model, whereLr=LrmaxandT=Tc, the authors are interested in the length of plasma fluid from the ablation surface to the critical density surface. The approximate analytical model can be expressed as follows:

Equation (23) and figure 4 are the relationships between the plasma length and the time in the conduction region. As can be seen from Eq. (23), when the pulse time and angleθare guaranteed, the desired increase in plasma length can be achieved by enhancing the intensity of the driving laser. Similarly,the plasma length can also be regulated by adjusting the pulse time and angleθwhen the laser intensity is determined.It can also be seen from Fig. 4 that the larger the angleθof the conical target,the smaller the length of the plasma will be when the pulse width is certain.

3. Verification and discussion

To verify the accuracy of the analysis results,the authors compared the results in this paper with a simulation program.A single-temperature computational fluid dynamics program based on Euler’s equation was utilized,[48]and the control equation is as follows:

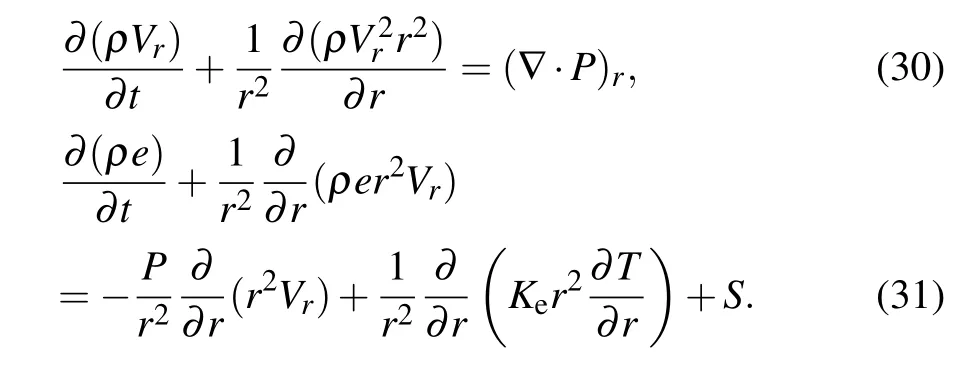
whereρ,Vr,e,T, andPrepresent the density, velocity, total energy, temperature, and pressure, respectively.Sis the laser energy deposition term induced by inverse bremsstrahlung absorption. The Spitzer–Harm model[49]was used for the electron heat transfer, andKeis the heat transfer coefficient. The finite volume method (FVM) was used for the fluid solution,with a non-uniform sparse grid being set at locations away from the target to extend the computational domain. Moreover, a dynamic grid function was added to ensure that the flow field remains in the encrypted grid. To compare the analytical results, the above equation is solved in a spherical coordinate system, and a one-dimensional laser shot problem is calculated taking into account the shrinkage effect.

The same conditions were set for the simulation and analysis model:driving laser power densityI=3.0×1014W/cm2,wavelengthλ=0.351 μm, and pulse widtht=1.0 ns. The comparison between the analysis results and the program simulation results is shown in Fig. 5, which includes the plasma density,temperature,pressure,and velocity in the conduction region of the conical target.

It is obvious from Fig. 5 that the analytical model developed in this paper and the numerical simulation results are generally consistent, although they show a small deviation in terms of values. This can be explained and their trends are consistent. In the model of this paper, when the laser is incident from the right, it can be seen that the left side of the conduction region is the compression zone. Therefore,the authors assume that the ablation surface also has a width,which leads to the fact that the plasma density at the ablation surface is unequal to the density of the solid fuel(Fig.5(a)).

In the analytical process, the temperature of the ablation surface is approximated as 0 keV for computational convenience. However, in Fig. 5(b), the authors combine the data given by the simulation results and compare the trend with the temperature simulation results, and find that they are in general agreement with each other. In the conduction region,the plasma temperature increases quickly initially and then slowly with the passage of time,and the authors approximate that the plasma temperature remains constant in the coronal region.

In Fig.5(c),the analytical results of the pressure and the simulation are in general agreement. In fact, the pressure decreases gradually and slowly from the ablation surface to the critical density surface, which can also be seen in the figure,but in the analysis, the authors approximate that it is an isobaric process,i.e.,the pressure remains essentially constant.

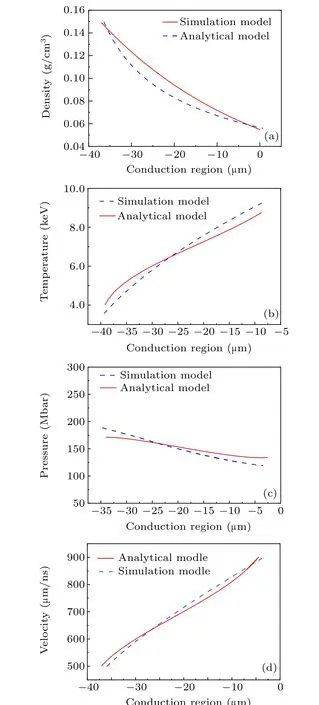
Fig. 5. Density (a), temperature (b), pressure (c), and velocity (d) in the conduction region. It is noteworthy that the authors take the critical density surface as the coordinate origin.

In the density model given in Eq.(12),adjusting the laser light intensity and pulse duration led to a change in the density gradient (Figs. 3 and 6), i.e., increasing the former two parameters reduces the gradient,but the effect is insignificant for the suppression ofγ. In other words,this adjustment in the proposed model has almost no effect on the Atwood number in Eq. (1). Therefore, the authors focus on the effect of the plasma length model on the RTI growth rate.

The ablation velocityVain Eq. (1) can be treated as a constant.[50]According to the model in this paper, the linear growth curvesγinfluenced by wavelengthλand the length of the plasma in the conduction zone are shown in Fig.7.but it is negligible. In order to observe more clearly the effect of the change in laser intensity onγ, the growth rate curveγinfluenced by laser intensity is shown here separately(Fig.9).

Fig. 6. Density curves at different laser intensities. The pulse width t=1.0 ns.

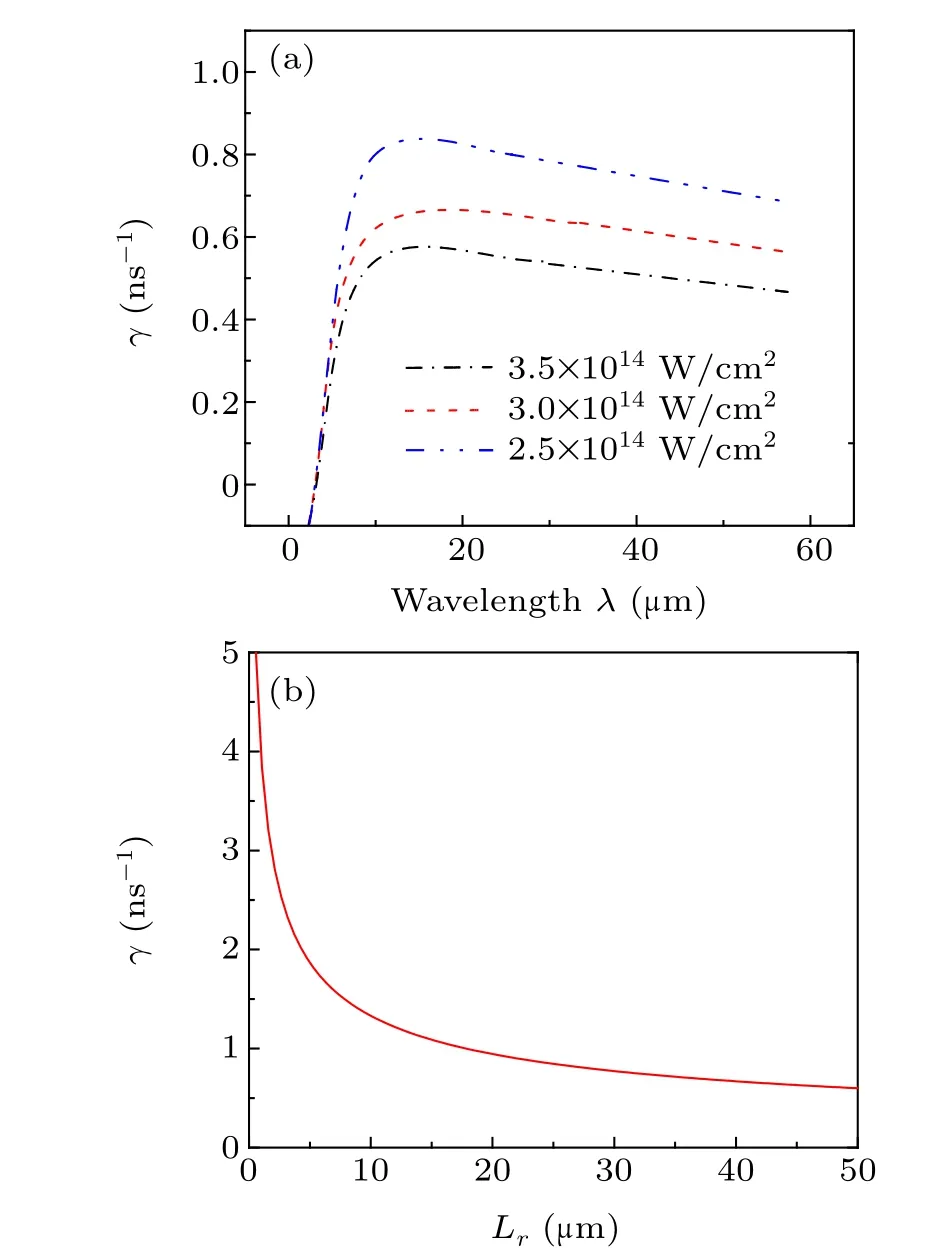
Fig.7.Linear growth curves γ influenced by wavelength λ (a)and Lr(b).For the selection of acceleration g,the authors refer to the values in the numerical simulation of ablation RTI by Ye et al.,[51]where g=17.85 μm/ns2.Atwood number A ≈0.5,and according to the model in this paper,ρ1 ≈0.054 g/cm3 and ρ2 ≈0.158 g/cm3. In(b),the perturbation wave number k=2π/λ and λ =0.351 μm.

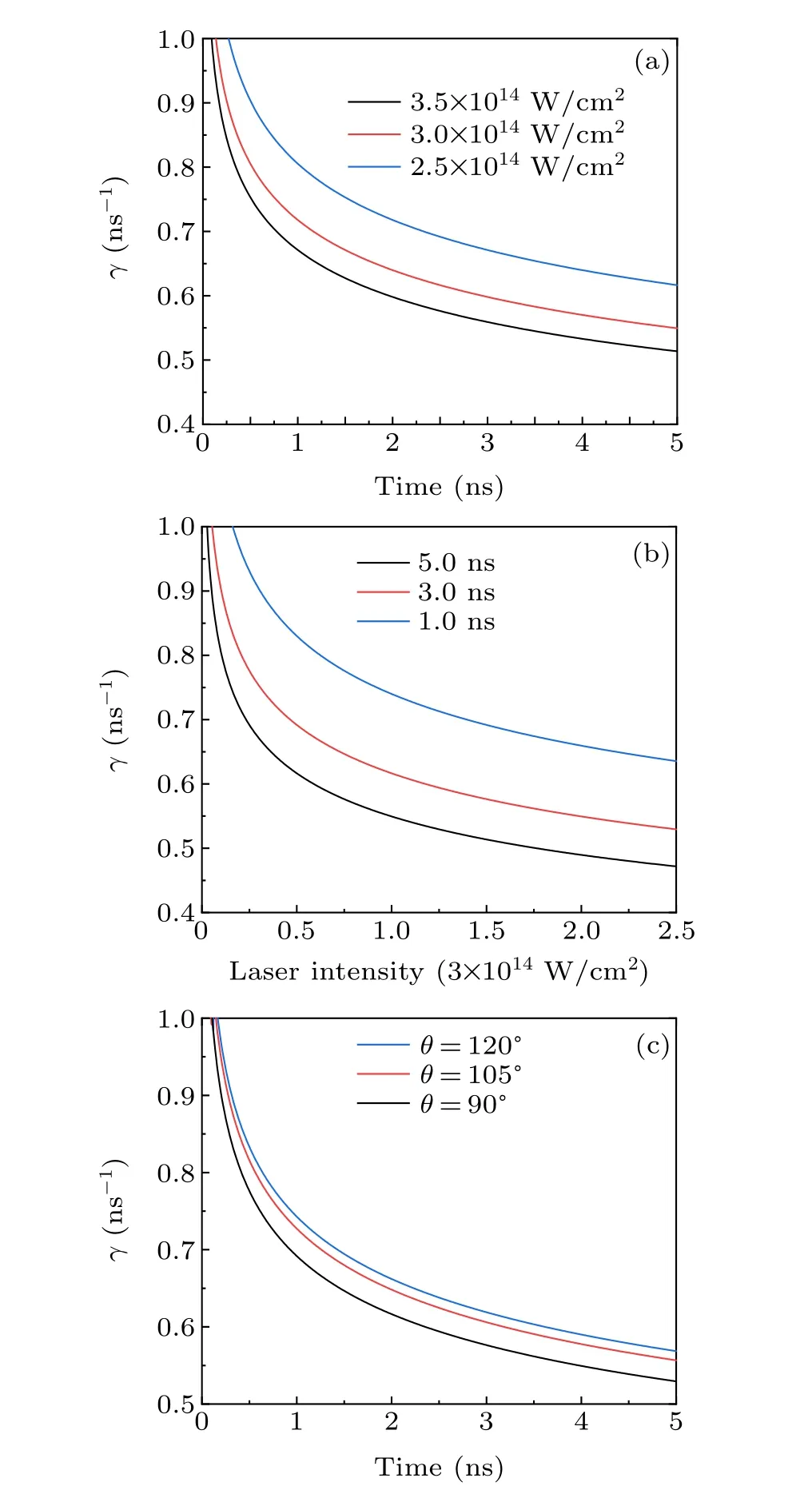
Fig. 8. Linear growth curves γ influenced by laser intensity (a), time (b),and angle θ of the conical target (c). In (a) and (b), the angle θ of the conical target is chosen to be 90°, and in (c), driving laser power density I=3.0×1014 W/cm2.

Overall,γdecays asLrincreases; however,which of the two,laser intensity or pulse time width,has a more significant effect on the growth rateγwill be discussed here(Fig.8).

Figure 8 shows that increasing the laser intensity and pulse duration or decreasing the angleθas appropriate can attenuate the RTI growth rate. It is worth noting that adjusting the laser pulse duration is more beneficial for attenuating the RTI growth rate,and changing the laser intensity has a limited impact onγ. The change in angleθalso has an effect onγ,

When the laser intensity is adjusted aroundI= 3.0×1014W/cm2in the experiment, the change in the growth rateγis minimal(Fig.9). There is only a fractional change in the order of magnitude. Moreover, it is necessary to drastically change the laser intensity to suppress the growth rate,but it is much easier and more efficient to alter the pulse duration.

Analytical solutions for the density, temperature, and length of the plasma are shown in Eqs. (12), (22), and (23),which are key works of this paper. Here the effect of the parameters in the proposed model on the RTI of the ablation surface is explicitly analyzed,emphasizing the significance of RTI analysis to the work in this paper. As the plasma length grows, the RTI caused by the density gradient is attenuated.When the angle of the conical target is 90°, appropriately increasing the pulse duration or increasing the laser intensity is beneficial to suppressing the growth rateγ. However, adjusting the pulse duration will be more efficient than changing the laser intensity.theoretical methods and mechanisms instead of only numerical solutions. The isobaric steady-state analytical model in the conduction region established in this paper demonstrates clear physical images and robust results, which are useful for analyzing the favorable conditions for attenuating RTI in a conical target.

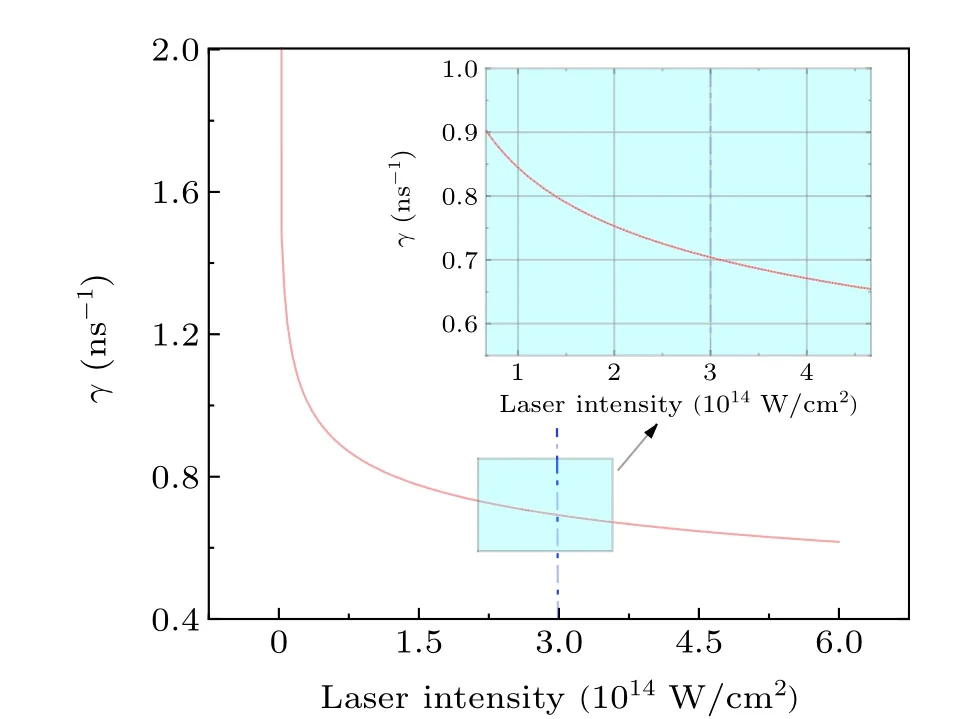
Fig.9. Partial enlargement of the growth rate curve γ. The baseline for the laser intensity is chosen here as I=3.0×1014 W/cm2,pulse width t=1.0 ns,and angle θ =90°.

4. Summary

In summary, an isobaric, steady-state model of a plasma fluid in the conduction zone is provided in this work to discuss and resolve the RTI present in the double-cone ignition scheme. Within the angle range of the conical target (90°–120°),the pulse width and laser intensity are appropriately increased when the angle is 90°,which is the most favorable for attenuating the RTI on the ablation surface,and increasing the pulse duration is more efficient than increasing the laser intensity and adjusting the angle(Fig.7). Notably,the study of the hydrodynamics of the plasma in the conical target conduction region using analytical methods has not been proposed at all in previous works.

Equations(12)and(23)show that laser intensity and time also affect the density trend in the conduction zone:increasing the laser intensity and pulse duration leads to a smaller density gradient and a longer lengthLof the plasma. The temperature solution of the energy equation of the fluid dynamics model is shown in Eq. (22). Increasing the laser intensity and time also increases the temperature near the critical density surface,which can have an impact on the temperature trend in the conduction zone. The two-dimensional calibration relations for the length, pressure, and velocity models of the plasma fluid in the conduction zone are provided by Eqs. (23), (24), and(28). The adjustable parameters inLrprovide convenience for the analysis of RTI on the ablation surface in the conical target.It can be concluded that extending the pulse duration is a more practical approach than increasing the laser intensity. Clearly,compared with the numerical simulation of two-dimensional fluid mechanics, the method proposed in this paper provides

Acknowledgment

Project supported by the Strategic Priority Research Program of Chinese Academy of Sciences (Grant Nos. XDA 25051000 and XDA 25010100).