Propulsive performance of a passively flapping plate in a uniform flow*

HAN Rui （韩瑞）， ZHANG Jie （张杰）， CAO Lei （曹垒）， LU Xi-yun （陆夕云）

1.State Key Laboratory of Urban and Regional Ecology， Research Center for Eco-Environmental Sciences，Chinese Academy of Sciences， Beijing 100085， China， E-mail： leicao@rcess.ac.cn

2. Department of Modern Mechanics， University of Science and Technology of China， Hefei 230026， China

Propulsive performance of a passively flapping plate in a uniform flow*

HAN Rui （韩瑞）1， ZHANG Jie （张杰）2， CAO Lei （曹垒）1， LU Xi-yun （陆夕云）2

1.State Key Laboratory of Urban and Regional Ecology， Research Center for Eco-Environmental Sciences，Chinese Academy of Sciences， Beijing 100085， China， E-mail： leicao@rcess.ac.cn

2. Department of Modern Mechanics， University of Science and Technology of China， Hefei 230026， China

Propulsive performance of a passively flapping plate in a uniform viscous flow has been studied numerically by means of a multiblock lattice Boltzmann method. The passively flapping plate is modeled by a rigid plate with a torsion spring acting about the pivot at the leading-edge of the plate， which is called a lumped-torsional-flexibility model. When the leading-edge is forced to take a vertical oscillation， the plate pitches passively due to the fluid-plate interaction. Based on our numerical simulations， various fundamental mechanisms dictating the propulsive performance， including the forces on the plate， power consumption， propulsive efficiency and vortical structures， have been studied. It is found that the torsional flexibility of the passively pitching plate can improve the propulsive performance. The results obtained in this study provide some physical insights into the understanding of the propulsive behaviors of swimming and flying animals.

propulsive performance， passively flapping plate， flapping-based locomotion， flexibility effect， propulsive efficiency

Introduction

A common strategy of flying or swimming animals for locomotion through a fluid is to employ their wings or fins to perform flapping motions［1-3］. The wings and fins are flexible and usually can generate the deformations during their flapping motions［4，5］. The deformations in turn affect the fluid dynamic forces［6，7］. Thus it is worth to understand the influence of flexibility on the flapping-based locomotion adopted by the swimming and flying animals.

The wings and fins have complex structural behaviors which are mainly related to the internal distribution of the compliant components. The wings and fins can be twisted easily to form a passive pitching motion. Because the large flexibility of wings or fins is mainly concentrated on the narrow and short root regions， the torsional flexibility can be assumed to be lumped together and be modeled by a torsion spring［8］. The lumped-torsional-flexibility model has been used to investigate the influence of flexibility on the locomotion of a passively flapping flat plate. The simplified model can reasonably predict the dynamics due to the fluid-plate interaction.

The flapping-based locomotion has attracted much attention due to the fundamental principles relevant to the swimming and flying animals. Extensive investigations with prescribed flapping motions have been carried out experimentally［9］and numerically［10，11］. In these studies the foil-like structures for modeling wings or fins are rigid rather than flexible and the flapping motions are prescribed rather than being passive. Recently， some studies on flapping flexible bodies have also been performed to analyze the effect of flexibility on the dynamic behaviors of the fluid-solid system［12-17］.

In this study， the propulsive performance of a passively flapping plate in a uniform viscous flow is investigated by solving the Navier-Stokes equations using a multiblock lattice Boltzmann method［6-8］. The flexibility of the plate is modeled by a lumped-torsional-flexibility model. The purpose of this study is to achieve an improved understanding of the mechanisms relevant to the flapping-based locomotion.

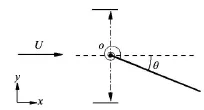
Fig.1 Sketch of a flapping and passive pitching plate

1. Physical problem and mathematical formulation

To investigate the flexibility effect of flapping wings and fins in animal locomotion， a lumped-torsional-flexibility model is used as shown in Fig.1 for the diagram. The flexibility of a plate is modeled by a torsion spring at the leading-edge of the plate O. When the edge is forced to take a vertical oscillation in a uniform viscous flow with the free-stream velocityU ，the plate pitches passively due to the fluid-plate interaction. Here， the oscillation of the edgeO is represented as

The incompressible Navier-Stokes equations are used to describe the flow dynamics which are given as

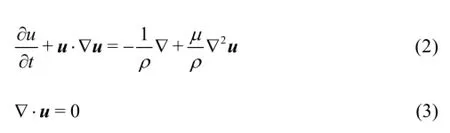
whereu is the velocity，p the pressure，ρthe density of the fluid， andµthe dynamic viscosity. The passively pitching motion of the plate with a torsion spring is governed by［8］

whereθrepresents the pitching angle，k denotes the spring stiffness， andIand Trare the moment of inertia of plate and the fluid moment with respect to the edgeO . The natural frequency of the plate-spring system is described as

Based on the non-dimensionalized analysis， the dimensionless parameters are given as follows： the flapping amplitude A=A/cwithc being the length of the plate， the Reynolds number Re=ρUc/µ， the linear density ratio of the plate and the fluid D=ρl/ ρc， and the frequency ratio of the natural frequency and the flapping frequency F=fn/f ， which is associated with the plate torsional flexibility［8］.

2. Numerical method and validation

The governing equations of the fluid-plate problem are solved numerically by a multiblock lattice Boltzmann method， which provides an alternative method for solving viscous fluid flows. Details of the numerical method and its validation have been given in our previous work［8，10］.

Based on a variety of examinations， the computational domain used in the present study is chosen as -30c≤x≤30cand -15c≤y≤15cwith the finest lattice spacing of 0.005c in the region around the plate and the coarsest spacing of0.04c near the far boundaries. The time step is 0.005T with the flapping periodT . It is confirmed that the computed results are independent of the lattice spacing and computational domain size.

In addition， the method and code used for this work have been validated carefully in our previous work described as follows. The numerical method has been applied with success to a wide range of flows，such as the propulsion of fishlike tail fins［3，10］， and the locomotion of a passively flapping flat plate［6，8］.

3. Results and discussion

We here present some typical results for the flow dynamics and propulsive performance of a passively flapping plate due to the fluid-plate interaction and discuss the connection of the results to the flappingbased locomotion of swimming and flying animals. Some quantities， such as the forces on the plate， the power consumption， the propulsive efficiency， the pitching angle， and vortex structures， are analyzed. Based on the measurements of animal locomotion， the governing parameters used here are chosen as the Strouhal number St =0.15-0.5， the frequency ratio F =1-10， the flapping amplitude A =0.3-0.7， the Reynolds number Re =1000and the density ratio D =1.

3.1Thrust force of the passively flapping plate

For the lumped-torsional-flexibility model in Fig.1， the plate generates a passive pitching motion due to a complicated interaction of the plate with the surrounding fluid flow. The forces exerting on the plate are responsible for the dynamic responses of the plate due to the fluid-plate interaction and are directlyrelated to the propulsive properties of the passive pitching plate. Based on our calculations， time-dependent forces will reach periodic state after two or three flapping cycles for all the cases considered here.

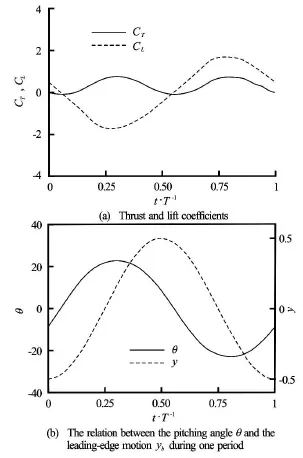
Fig.2 Time-dependent force coefficients and pitching angle of the flapping plate for A =0.5，St =0.3and F=2.5

To elucidate the dynamic behavior and the passive pitching motion of the plate， Fig.2 typically shows the thrust and lift coefficients and the pitching angle θduring one cycle after reaching the periodic state. Here， the thrust and lift coefficients are defined as， respectively，

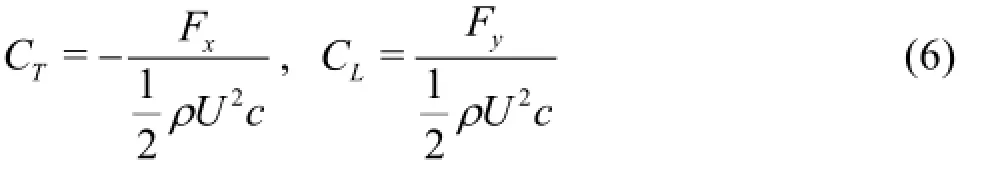
where -Fxand Fyrepresent the time-dependent thrust and lift acting on the plate due to pressure and viscous friction. The thrust and lift coefficients are shown in Fig.2（a）. The positiveCTon most part of the period is formed which plays an essential role for the propulsion of the passive pitching plate. The variation ofCLis exhibited with its mean value over one period vanishing. It is also identified that CLvaries with the vortex shedding frequency from the flapping plate.

For the model considered here， the passive pitching motion can be characterized by the pitching angle θ（t）as shown in Fig.1. The phase shiftφbetween the leading-edge oscillationyb（t）in Eq.（1） and the pitching angleθ（t）is an important parameter to understand the propulsive behavior. The profiles of yb（t ）and θ（t）during one cycle are shown in Fig.2（b）and the phase shiftφ=70oapproximately is obtained. Thus， an advanced phase shift ofθ（t）with respect to yb（t）occurs， which is associated with the locomotion of the passive flapping plate［1］.

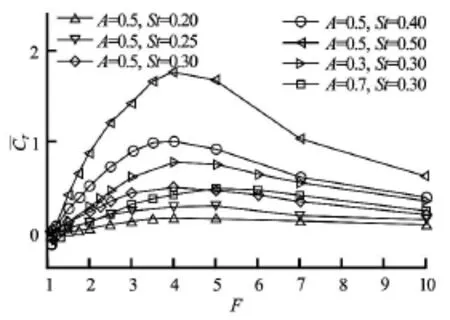
Fig.3 Mean thrust coefficientversus the frequency ratio F for several pairs of the flapping amplitudeAand the Strouhal numberSt

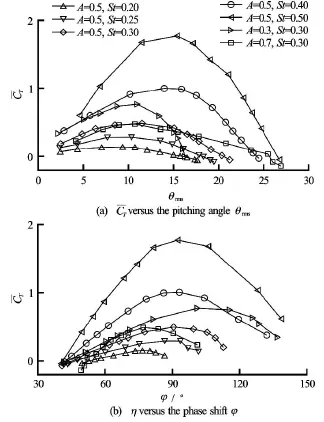
Fig.4 Mean thrust coefficientand propulsive efficiencyη

Based on a variety of simulations in a wide range of the parameters， the features of the mean thrust， the pitching angle and the phase shift are further discussed. Figure 3 shows the mean thrust coefficientversus the frequency ratioF for several pairs of flapping amplitudeA and frequencySt. For each pair ofAandSt， theincreases to its maximum in the range of F=3-6approximately， and then decreases gradually with the further increase ofF. From the profiles of A =0.5and St =0.2-0.5， theis enhanced with the increase ofSt. From the results of St =0.3and A =0.3， 0.5 and 0.7， thedecreases essentially with the increase ofA. The behaviors of the thrust evolution are associated with the pitching angle and the phase shift due to the fluid-plate interaction. Figure 4 shows the mean thrust coefficientversus the pitching angle and the phase shift for the calculated cases in Fig.3. It is identified that the higher mean thrust coefficientcorresponds to the region of the pitching angle=10o-20oand the phase shiftφ=70o-90o.

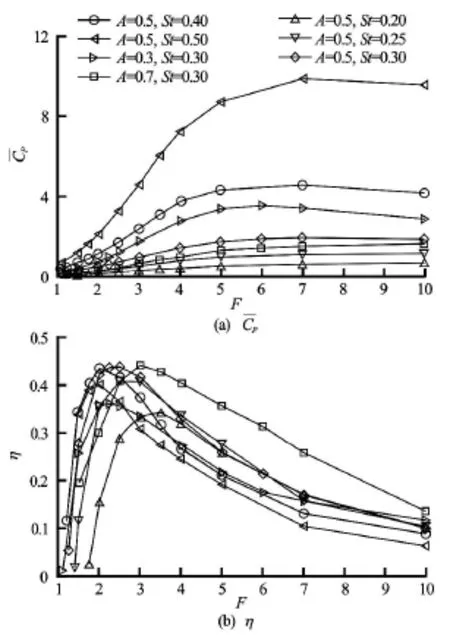
Fig.5 Mean power coefficientand propulsive efficiency η versus the frequency ratio

3.2Power consumption and propulsive efficiency

The propulsive property is investigated in terms of the propulsive efficiency. The power required to produce the passive pitching motion of plate is described as

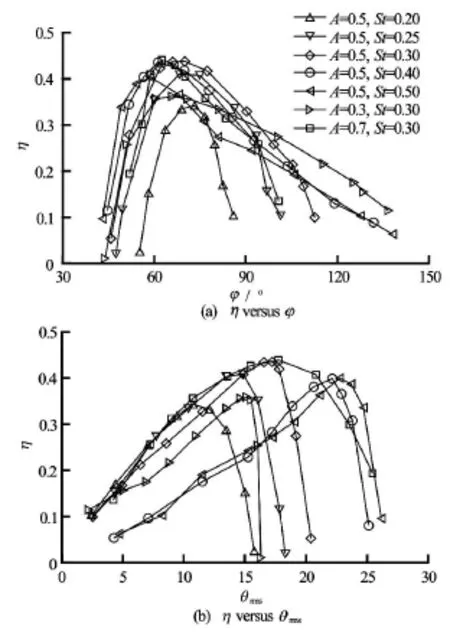
Fig.6 Propulsive efficiencyηas function of the phase shiftφ and the pitching angle θrms

Figure 5 shows the mean power coefficient and the propulsive efficiency. For each pair ofAandSt，the mean power coefficientin Fig.5（a） increases to its maximum in the range of F=5-7and decreases slightly with the further increase ofF， which is essentially consistent with the mean thrust coefficientin Fig.3. It means that a larger production of thrust needs a higher consumption of power. As shown inFig.5（b） for the propulsive efficiency η， a higher propulsive efficiency lies in F=1.5-4， corresponding to the range adopted by swimming animals which will be discussed below.

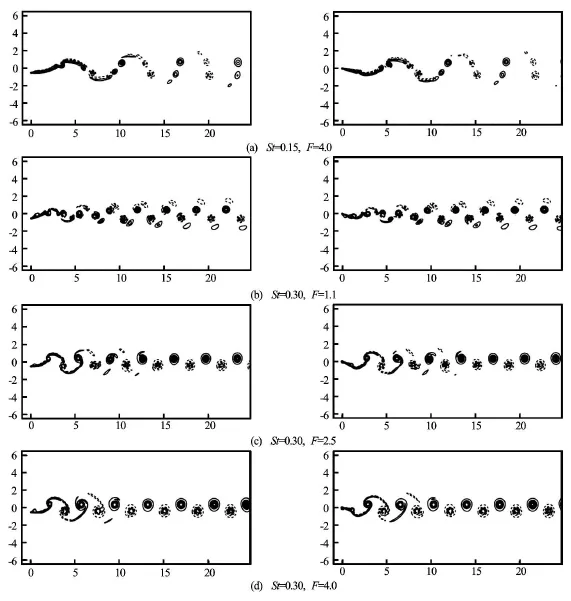
Fig.7 Instantaneous vorticity contours at t/T =0/4（left column） and 1/4 （right column） for A=0.5. Solid and dashed lines represent positive and negative values， respectively

The increase ofFrepresents that the spring becomes stiffer in the plate-spring system in Eq.（4）. Thus， the motion of the passive pitching plate tends to the rigid case at a large value ofF ， such as F=10. As an example， considering the results forA=0.5 and St=0.3in Fig.5（b）， the highest efficiency is about 0.44 atF=2.5and is enhanced by 267% with respect to the efficiency of the rigid model about 0.12. Thus， the torsional flexibility effect can remarkably improve the propulsive efficiency.

The propulsive efficiency is associated with the phase shiftφand the pitching angle θrms［1］. Fig.6（a） shows the propulsive efficiencyηversus the phase shift φ. With the increase ofφ， the propulsive efficiencyηincreases to a peak and then decreases for a given pair ofAandSt . The higher efficiency is reached during φ=60o-80o. Moreover， Fig.6（b） shows the propulsive efficiencyηversus the pitching angle θrms. It is seen that high efficiency is generated for=10o-25oapproximately.

3.3Vortex structures behind the flapping plate

The vortex structure around the plate is closely associated with the dynamic characteristics of the plate［10，18］. We further discuss the vortex shedding to understand propulsive performance of the passive flapping plate. To neatly exhibit the flow patterns， Fig.7 shows the vorticity contours at instants t/T=0/4 and 1/4 forA =0.5with several pairs of StandF. The shear layer is generated along the surface and is gradually shed into the downstream of the plate to form concentrated vortices. As shown in Fig.7（a） forSt= 0.15， the separated shear layer due to its unstable character evolves into three positive and negative concen-trated vortices during one flapping cycle. With the increase ofSt ， there exist two vortices with opposite sign shed downstream during one cycle as shown in Fig.7（d）. Finally， a reverse von Kármán vortex street occurs in the wake of the plate， which induces a jetlike mean velocity profile in the wake and is of help in generation of the thrust.

To analyze the effect of the frequency ratioF on the vortex structures， Figs.7（b）-7（d） show the vortex patterns for F =1.1， 2.5 and 4.0 with St=0.3. Usually， the lower frequency ratio means that the flexibility effect becomes more important. As shown in Fig.7（b）forF=1.1， the shear layer separated from the plate evolves into two positive and negative concentrated vortices during one flapping cycle. With the increase ofF， only two vortices with opposite sign are shed during one cycle in Fig.7（d） for F=4.0. In addition，with the evolution of the vortex structures forF=1.1，a reverse von Kármán vortex street is eventually formed in the somewhat far wake of the plate， which is responsible for the thrust generation.

4. Concluding remarks

The propulsive performance of a passively flapping plate in a uniform flow has been studied by means of a multiblock lattice Boltzmann method. We have investigated various mechanisms related to the dynamics of the flapping plate due to the fluid-plate interaction based on the results of the forces exerting on the plate， the power consumption， the propulsive efficiency， the pitching angle and vortex structures.

Based on the simulations in a wide range of the parameters， the features of the mean thrust， the pitching angle and the phase shift are analyzed. It is found that the torsional flexibility of the passively pitching plat can improve the propulsive performance. The propulsive property is analyzed based on the propulsive efficiency. A larger production of thrust needs a higher consumption of power. In addition， the effects of the frequency ratio and Strouhal number on the vortex structure around the plate are investigated. The reverse von Kármán vortex street is closely associated with the propulsive behavior of the plate. The results obtained in this study can provide some physical insights into the understanding of the propulsive behaviors of swimming and flying animals.

References

［1］TRIANTAFYLLOU M. S.， TRIANTA- FYLLOU G. S. and YUE D. K. P.Hydrodynamics of fishlike swimming［J］. Annual Review of Fluid Mechanics， 2000，32（1）： 33-53.

［2］WANG Z. J.Dissecting insect flight［J］. Annual Review of Fluid Mechanics， 2005， 37（1）： 183-210.

［3］LI Gao-jin， ZHU Luoding and LU Xi-yun. Numerical studies on locomotion performance of fishliketail fins［J］. Journal of Hydrodynamics， 2012， 24（4）： 488-495.

［4］COMBES S. A.， DANIEL T. L. Flexural stiffness in insect wings. I. Scaling and the influence of wing venation［J］. Journal of Experimental Biology， 2003， 206：2979-2987.

［5］COMBES S. A.， DANIEL T. L. Flexural stiffness in insect wings. II. Spatial distribution and dynamic wing bending［J］. Journal of Experimental Biology， 2003，206： 2987-2997.

［6］HUA R.， ZHU L. and LU X.Locomotion of a flapping flexible plate［J］. Physics of Fluids， 2013， 25（12）：121901.

［7］HUA R.， ZHU L. and LU X. Dynamics of fluid flow over a circular flexible plate［J］. Journal of Fluid Mechanics， 2014， 759： 56-72.

［8］ZHANG J.， LIU N. and LU X. Locomotion of a passively flapping flat plate［J］. Journal of Fluid Mechanics，2010， 659： 43-68.

［9］BIRCH J. M.，DICKINSON M. H.Spanwise flow and the attachment of the leading-edge vortex on insect wings［J］. Nature， 2001， 412（6848）： 729-733.

［10］LI G.， LU X. Force and power of flapping plates in a fluid［J］. Journal of Fluid Mechanics， 2012， 712： 598-613.

［11］WANG Ya-yun， HU Wen-rong and ZHANG Shi-dong. Performance of the bio-inspired leading edge protuberances on a static wing and a pitching wing［J］. Journal of Hydrodynamics， 2014， 26（6）： 912-920.

［12］HEATHCOTE S.， GURSUL I. Flexible flapping airfoil propulsion at low Reynolds numbers［J］. AIAA Journal，2007， 45（5）： 1066-1079.

［13］HEATHCOTE S.， WANG Z. and GURSUL I.Effect of spanwise flexibility on flapping wing propulsion［J］. Journal of Fluids and Structures， 2008， 24（2）： 183-199.

［14］MICHELIN S.， SMITH S. G. L.Resonance and propulsion performance of a heaving flexible wing［J］. Physics of Fluids， 2009， 21（7）： 429-445.

［15］ELDREDGE J. D.， TOOMEY J.and MEDINA A. On the roles of chord-wise flexibility in a flapping wing with hovering kinematics［J］. Journal of Fluid Mechanics， 2010， 659： 94-115.

［16］FERREIRA SOUSA P. J.， ALLEN J. J.Thrust efficiency of harmonically oscillating flexible flat plates［J］. Journal of Fluid Mechanics， 2011， 674： 43-66.

［17］KANG C.， AONO H. and CESNIK C. E. S. et al. Effects of fiexibility on the aerodynamic performance of flapping wings［J］. Journal of Fluid Mechanics， 2011，689： 32-74.

［18］WU J.， LUX. and ZHUANG L. Integral force acting on a body due to local flow structures［J］. Journal of Fluid Mechanics， 2007， 576： 265-286.

（November 9， 2014， Revised April 15， 2015）

* Project supported by the Natural Science Foundation of China （Grant No. 11372304）， the 111 Project （Grant No. B07033）.

Biography： HAN Rui （1986-）， Female， Ph. D.

LU Xi-yun， E-mail： xlu@ustc.edu.cn