Investigating the UV-excess in Star Clusters with N-body Simulations:Predictions for Future CSST Observations*

Xiaoying Pang , Qi Shu, Long Wang , and M. B. N. Kouwenhoven

1 Department of Physics, Xi’an Jiaotong-Liverpool University, Suzhou 215123, China; Xiaoying.Pang@xjtlu.edu.cn

2 Shanghai Key Laboratory for Astrophysics, Shanghai Normal University, Shanghai 200234, China

3 School of Physics and Astronomy, Sun Yat-sen University, Zhuhai 519082, China

4 Department of Astronomy, School of Science, The University of Tokyo, Tokyo 113-0033, Japan

5 RIKEN Center for Computational Science, Kobe, Hyogo 650-0047, Japan

Abstract We study the origin of the UV-excess in star clusters by performing N-body simulations of six clusters with N=10 k and N=100 k (single stars & binary systems) and metallicities of Z=0.01, 0.001 and 0.0001, using PETAR.All models initially have a 50%primordial binary fraction.Using GalevNB we convert the simulated data into synthetic spectra and photometry for the China Space Station Telescope(CSST)and Hubble Space Telescope(HST). From the spectral energy distributions we identify three stellar populations that contribute to the UVexcess:(1)second asymptotic giant branch stars,which contribute to the UV flux at early times;(2)naked helium stars and(3)white dwarfs,which are long-term contributors to the FUV spectra.Binary stars consisting of a white dwarf and a main sequence star are cataclysmic variable (CV) candidates. The magnitude distribution of CV candidates is bimodal up to 2 Gyr. The bright CV population is particularly bright in FUV-NUV. The FUV-NUV color of our model clusters is 1–2 mag redder than the UV-excess globular clusters in M87 and in the Milky Way. This discrepancy may be induced by helium enrichment in observed clusters. Our simulations are based on simple stellar evolution; we do not include the effects of variations in helium and light elements or multiple stellar populations.A positive radial color gradient is present in CSST NUV-y for main sequence stars in all models with a color difference of 0.2–0.5 mag,up to 4 half-mass radii.The CSST NUV-g color correlates strongly with HST FUV-NUV for NUV-g ＞1 mag, with the linear relation FUV-NUV=(1.09±0.12)×(NUV-g)+(-1.01±0.22). This allows for conversion of future CSST NUV-g colors into HST FUV-NUV colors,which are sensitive to UV-excess features.We find that CSST will be able to detect UVexcess in Galactic/extragalactic star clusters with ages ＞200 Myr.

Key words: methods: numerical – (stars:) binaries: general – stars: kinematics and dynamics

1. Introduction

Excess of ultraviolet (UV) emission between the Lyman break (1216 Å) and 2500 Å in the spectral energy distribution(SED) was unexpectedly found in many early-type galaxies.This phenomenon is called the “UV-upturn” or the “UVexcess”(Code&Welch 1979;Burstein et al.1987;O’Connell et al. 1992; Dorman et al. 1995), after the first UV-upturn discovery made in the bulge of M31 (Code & Welch 1979).The strength of the UV-upturn tends to rise with increasing stellar mass of a galaxy (Dantas et al. 2020), with a higher metallicity (Burstein et al. 1988), and with increasing age(Smith et al. 2012). The evolution of the UV-upturn with redshift is still under debate (Ali et al. 2018; Dantas et al.2020).

The corresponding effective temperature for the UV-upturn feature should be above 20,000 K (Brown et al. 1997).However,most of the early-type galaxies are quiescent in their star formation (Welch 1982; Oconnell et al. 1986; Buzzoni et al. 2012). The hot O-B stars (30,000–40,000 K) cannot contribute to the UV-excess emission (Buzzoni et al. 2012).Numerous studies have been carried out to identify the candidates that contribute to the observed UV-excess. Old,hot and low-mass stars have been a popular choice. These include,for example,post-asymptotic giant branch(AGB)stars(Greggio&Renzini 1990)and regular AGB stars (Guerrero &Ortiz 2020); extreme horizontal branch stars (EHB, Yi et al.1997; Yoon et al. 2004; Ree et al. 2007); and young white dwarfs(WDs)that are hot and blue(Mestel 1952;Rauch et al.2014;Torres et al.2014;Pang et al.2016).On the other hand,interacting binary systems containing subdwarfs have also been a proposed source of the UV-upturn (Zhang et al. 2005; Han et al. 2007, 2010).

All these candidate populations of stars are present in clustered stellar environments. UV-excess emission has been found in several old Galactic globular clusters (GCs): 47 Tuc(O’Connell et al.1997),NGC 6388 and NGC 6441(Rey et al.2007); and in the old open cluster NGC 6791 (Buzzoni et al.2012). EHB stars are present in each of these clusters, and are thought to produce the observed UV-excess (Yi et al. 1999;Yoon et al.2006).Fan et al.(2020)report five star clusters with ages of around 1 Gyr in M33 with UV-excess.A large number of GCs with strong UV emission was revealed in M87 (Sohn et al. 2006). The population of GCs in M87 is distinct from those of the Milky Way (MW) (Dorman et al. 1995) or Local Group counterparts. They are generally more metal-rich (near solar abundance)than MW GCs,and are typically 1 magnitude bluer than the early-type galaxies in far-UV (FUV)-V color.The EHB stars generated by the metal-rich and helium enhancement model (Lee et al. 2005; Chung et al. 2011;Bekki 2012) appear to be promising candidates for the UV features found in the GCs of M87.

The presence of multiple populations can also dramatically affect the UV color of star clusters (Milone et al. 2018, 2020;Zennaro et al. 2019; Jang et al. 2021). A second population of stars enhanced in helium from Y=0.25–0.26 up to Y ＞0.40 can produce hot and blue horizontal branch stars that are major contributors to the UV flux. These are proposed in theoretical studies and are also confirmed by spectroscopic measurements(D’Antona & Caloi 2008; Tailo et al. 2019, 2020; Marino et al.2014;Milone et al.2018).Jang et al.(2021)have provided direct evidence of the effect of multiple populations on the integrated colors of Galactic GCs based on Hubble Space Telescope(HST)photometry. The second generation of stars with helium enrichment is bluer in the UV and is hotter than the first generation stars.However,in this work,we focus on simple stellar populations with a pristine helium and light element abundance,with the motivation to search for the stellar candidates making contribution to the UV colors of the star clusters.The inclusion of multiple stellar populations and helium variations is beyond the scope of the current study, and deserves further future investigation.

Studying the UV-excess candidate stars in a cluster environment can greatly benefit from N-body simulations using sophisticated codes such as those in the NBODY6(++) family(Spurzem 1999; Aarseth 2003; Spurzem et al. 2008; Nitadori &Aarseth 2012; Wang et al. 2015), PETAR (Wang et al. 2020a) or AMUSE (Portegies Zwart et al. 2013). Such N-body simulations can be used to trace the dynamical history of individual stars and binary systems with high precision, can resolve the binary orbits and can accurately model the processes of stellar evolution(wind mass loss,evolution of stellar radii and core radii)of all stars and multiple systems in star clusters.

N-body simulations produce physical and kinematical properties of the stellar population over time. In order to be able to compare these data with observations,Pang et al.(2016)developed the code GalevNB, which converts fundamental physical stellar properties, such as stellar mass, temperature,luminosity and metallicity, into observables for a variety of filter bands used by mainstream instruments/telescopes, such as HST, European Southern Observatory (ESO), Sloan Digital Sky Survey (SDSS) and Two Micron All-Sky Survey(2MASS), and into spectra that span the FUV (90 Å) to the near-infrared (IR) (160 μm). Combining GalevNB with Nbody simulations allows for a direct comparison between observational data and numerical results. It is also possible to trace the photometric and dynamical evolution of the individual stars or binary systems that are candidates for the UV-upturn.

The future China Space Station Telescope(CSST)will feature a collecting surface with a diameter of 2 meters, and observe at wavelengths ranging from the near-UV(NUV)at 0.255 μm to the IR at 1.7 μm. CSST is expected to have a spatial resolution≾0.15″(Cao et al. 2018; Gong et al. 2019). The limiting magnitudes in the g-band and NUV-band are 26.3 mag and 25.4 mag respectively, which will extend down to 27.5 mag and 26.7 mag for the ultra-deep-field observations.CSST will thus be an essential tool for observing extragalactic objects at a later time than the HST,especially for star clusters in Local Group galaxies.

In this study,we investigate the sources of UV-excess in star clusters using N-body simulations, and through employing GalevNB to obtain synthetic CSST magnitudes of six filters:NUV (2500–3000Å), g, r, i, z, y; and HST/Space Telescope Imaging Spectrograph (HST/STIS) FUV and NUV(1500–3000 Å) filters. This enables us to analyze the spectral and photometric features of the simulated star clusters and search for the sources of UV-excess in the wavelength range of 1216–2500 Å. By means of synthesizing observations from Nbody simulations, we aim to determine the sensitivity and efficacy of the CSST for detecting UV-excess in star clusters.

This paper is organized as follows.Section 2 introduces the Nbody code PETAR and the initial conditions for the stellar and binary populations in our models.Section 3 presents the SEDs of the modeled star clusters and identifies the candidate stellar populations that can produce the UV-excess. In Section 4, we show the photometric features in the CSST and HST filter bands for the simulated clusters after conversion with GalevNB.Section 5 investigates the properties of normal detached binary stars and the UV-excess candidate binary stars.In Section 6.1,we compare the HST/STIS colors of the simulated clusters to those of star clusters with observed UV-excess.In Section 6.2,we provide predictions of the sensitivity of CSST for studying star clusters with UV-excess.Finally,we summarize our findings in Section 7.

2. N-body Simulations

2.1. N-body Code PETAR

In order to model the evolution of star clusters and their stellar populations, it is necessary to accurately follow the dynamical and stellar evolution of both stars and binarysystems.To achieve this,we use the high-performance N-body code PETAR (Wang et al. 2020b) to carry out star cluster simulations. PETAR combines the particle-tree and particleparticle algorithm (Oshino et al. 2011) and slow-down algorithmic regularization (Wang et al. 2020a). The former is a hybrid method that implements the Barnes-Hut tree method(Barnes & Hut 1986) for efficiently calculating the long-range interaction between particles (stars) and the 4th order Hermite integrator (e.g., Aarseth 2003) for accurately evaluating the short-range interactions between the constituents of the system.The latter is specifically designed for integrating the orbits of particles in multiple systems, including close encounters between stars, binary systems and higher-order few-body systems. PETAR has been developed based on the framework for developing parallel particle simulator (FDPS) codes, which can achieve a high performance by using multi-process parallel computing (Iwasawa et al. 2016, 2020; Namekata et al. 2018).

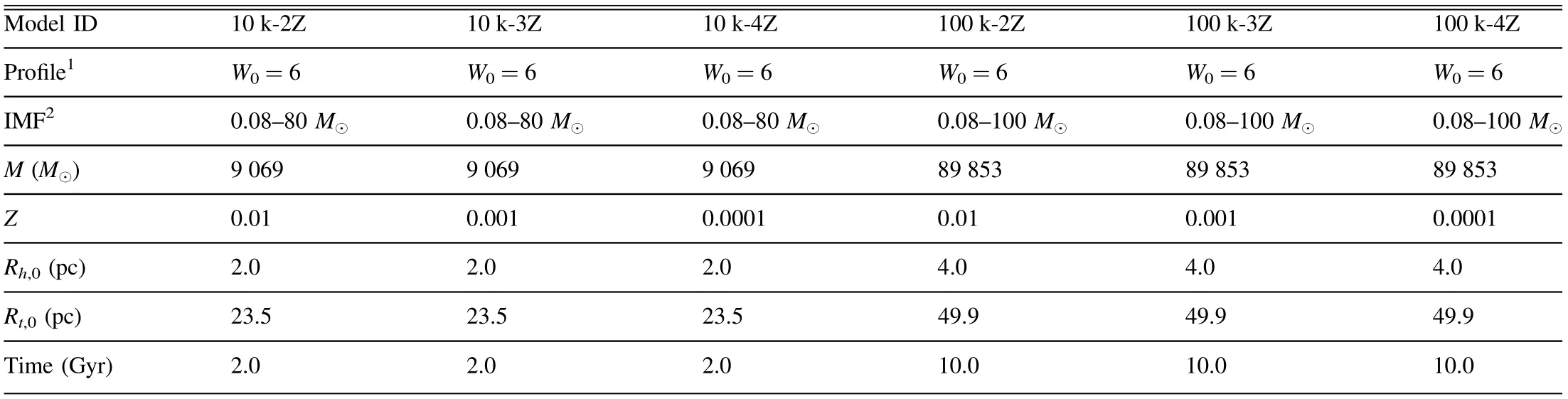
Table 1 Initial Conditions for the Six Star Cluster Models

The recently-updated single and binary stellar evolution codes, SSE and BSE respectively(Tout et al.1997;Hurley et al.2000, 2002; Banerjee et al. 2020), are both utilized in PETAR.Unlike computationally-expensive hydro-dynamical modeling of stellar evolution,these population synthesis codes provide a reasonable approximation of stellar evolution while the computational cost is negligible when compared to that of the integration of the N-body system. The stellar evolution model of Banerjee et al. (2020) uses semi-empirical stellar wind prescriptions from Belczynski et al.(2010).We adopt the“rapid”supernova model and material fallback from Fryer et al.(2012), along with the pulsation pair-instability supernova model (Belczynski et al. 2016) for the formation of compact objects.

2.2. Initial Conditions

We simulate the evolution of six star clusters using PETAR.Three models are initialized with N = 10,000 particles (10 k),and the other three with N = 100,000 (100 k) particles. The PETAR code represents each particle as an individual star in the cluster. The initial parameters for the models are set up using the MCLUSTER version provided by Kamlah et al. (2021),which is updated from the original MCLUSTER of Küpper et al.(2011).We carry out three simulations of models with N=10 k and N=100 k by assigning three metallicities,Z=0.01(-2Z),0.001 (-3Z) and 0.0001 (-4Z), representing metal-rich,intermediate and metal-poor star clusters respectively. We refer to these six models as 10 k-2Z, 10 k-3Z, 10 k-4Z, 100 k-2Z, 100 k-3Z and 100 k-4Z, respectively.

PETAR does not include gas dynamics. We therefore start simulations from virial equilibrium, after all gas has been expelled by stellar radiation and wind feedback from massive stars. We adopt a tidal field corresponding to that of a circular orbit in the solar neighborhood.The 10 k and 100 k models are evolved until 2 Gyr and 10 Gyr, respectively. The simulation time is shorter in lower-mass clusters, as these disrupt faster than higher-mass star clusters.

Models with identical particle numbers (i.e., 10 k or 100 k)are initialized with the same distributions of masses, positions and velocities. All cluster models follow a King (1966) initial density profile with a dimensionless King parameter of W0=6,and are assigned with initial half-mass radii of Rh,0=2.0 pc for the 10 k models and Rh,0=4.0 pc for the 100 k models. We adopt the initial mass function (IMF) of Kroupa (2001) for all models,with a mass range 0.08–80 M⊙for the 10 k models and 0.08–100 M⊙for the 100 k models. All clusters are initialized in virial equilibrium, Q=0.5, where the virial ratio Q=|T/U|is the ratio between the total kinetic energy (T) and the total potential energy (U) of the star cluster. We summarize the initial conditions of all models in Table 1.

2.3. Binary Setup

All star cluster models are initialized with a 50% primordial binary fraction(B/(B+S)),i.e.,the total number of single stars(S)in each cluster equals the total number of binary systems(B)in the cluster. For example, in the N=S+B=10k models,there are S=5000 single stars and B=5,000 primordial binary systems (i.e., a total of 2B=10,000 stars in binary systems).The primordial binary systems are assigned a mass ratio, a semimajor axis and an eccentricity as described below. We define the mass ratio of a binary system consisting of two stars of masses m1and m2as q=m2/m1, where m2≤m1.

For stellar masses below 5 M⊙, the masses of both binary components are generated through random pairing from the IMF. For stars with masses above 5 M⊙, the mass of the primary star (m1) is randomly selected from the IMF, and the secondary mass m2=q m1is subsequently assigned after drawing the mass ratio from a uniform distribution(0.1 ＜q ＜1, Sana et al. 2012) in the mass range 0.08 M⊙≤m2≤80(100)M⊙. As a consequence of this initial setup,the number of massive stars(＞5 M⊙)in binary systems is roughly double that of the number of massive single stars.We refer to Kouwenhoven et al. (2009) for an extensive discussion on how the choice of random pairing affects the binary fraction and the mass ratio distribution for different primary star mass ranges.

The initial semimajor axis distribution of the primordial binary systems follows a uniform distribution inlogain the range 0.05–50 au. The lower limit of the semimajor axis distribution arises from the physical size of the stars,while the upper limit is comparable to the hard-soft boundary in star clusters based on the Heggie-Hills law (Heggie 1975;Hills 1975). The initial eccentricity distribution is thermal:f(e)∝e (see, e.g., Heggie 1975; Goodman & Hut 1993). We adopt the eigenevolution and feeding algorithms of Kroupa et al. (2013). All binary systems are assigned random spatial orientations and a random orbital phase.

3. Spectral Energy Distributions

After having completed the simulations of the six models,we use GalevNB (Pang et al. 2016) to convert the theoretical data produced by the N-body simulations (stellar mass,temperature, luminosity and metallicity) into observational magnitudes of HST/STIS and CSST filters, and into spectra that span far-UV to near-IR wavelengths.Individual spectra are produced for each star by selecting or interpolating template spectra from the Lejeune et al. (1997) spectral library.GalevNB sums up the fluxes of individual stars and produces the integrated SEDs of the simulated clusters. In order to quantify the individual contributions of particular stellar populations to the integrated SED of a cluster, we also separately sum up the SEDs for specific populations, such as single stars,binary systems and stars of a certain spectral type.The abbreviations for the different spectral types are listed in Table 2.

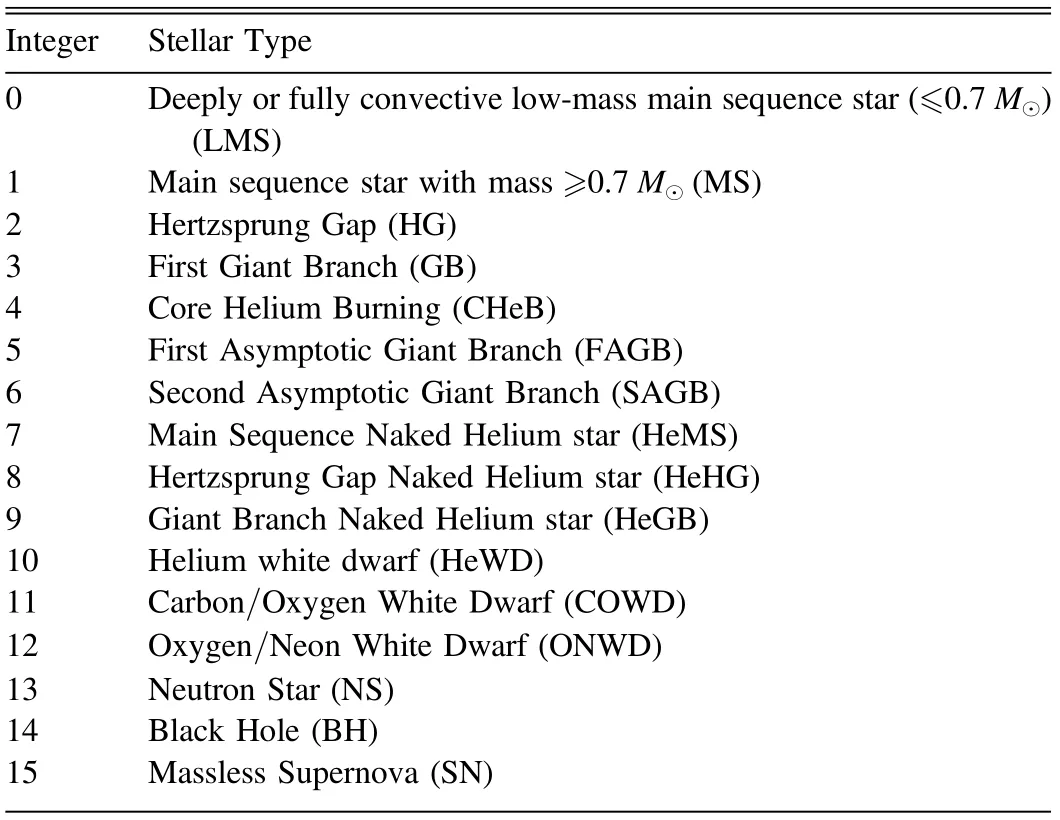
Table 2 Stellar Types Defined in PETAR

3.1. Candidate Stars Contributing to the UV-excess

In panels(a)(1)–(4)of Figures 1 and 2,we display the SEDs of models 10 k-2Z and 100 k-4Z, for the entire timespan of the simulations (Figure 1(a)(1)–(4)). The SED of single and binary stars are presented in Figure 1(b)(1)–(4) and (c)(1)–(4),respectively. The SEDs of the other models are shown in Appendix A.The number of individual stars in binary systems is initially double the number of single stars (see Section 2.3).Therefore, the population of massive stars in binary systems contributes more UV flux(1216 Å ＜λ ＜2500 Å)during the first 100 Myr (Figure 1(c)(1)–(4)). In the 10 k metal-poor models(10 k-3Z and 10 k-4Z), binaries dominate the UV flux when t ＜200 Myr.For the 100 k models,the contribution of the binary systems to the UV-excess occurs much earlier, mainly at times t ＜70 Myr (100 k-2Z), t ＜80 Myr (100 k-3Z) and t ＜100 Myr(100 k-4Z).

3.1.1. Second Asymptotic Giant Branch (SAGB)

In order to identify the UV-excess candidate stars, we plot the SEDs of single stars (panels(b)(1)–(4) of Figures 1 and 2) and binary systems(panels(c)(1)–(4)),in which the contribution to the SEDs by each spectral type is indicated with a different color.

We identify three populations of candidate stars that provide a significant contribution to the UV-excess in the clusters.When the clusters are young, the second asymptotic giant branch (SAGB,cyan curve) stars generate a peak in the UV range when t ＜200 Myr in the 10 k models. This population continues to contribute to the UV flux until t ≈700 Myr in the 100 k models.However, although their UV luminosity is high, SAGB stars are short-lived. Only when stars are sufficiently massive (4–8 M⊙)can they enter the SAGB phase.At this time,the hydrogen shell is re-ignited due to a second dredge-up, and it grows together with the helium-burning shell. A helium shell flash occurs, which releases a large amount of energy(Hurley et al.2000)for SAGB stars; this generates a UV peak.

Figure 1.The SED of model 10 k-2Z.Panels(a)(1)–(4)are for the entire cluster(dotted blue curves),for the single stars(solid orange curves)and for binary systems(solid green curves).(b)(1)–(4),(c)(1)–(4)The SEDs for single stars and binary systems,respectively,in which we specify the contributions of populations of different spectral types (see Table 2) to the SED.

3.1.2. Naked Helium Stars (HeMS)

Another group of candidates is the main sequence naked helium (HeMS) stars. When massive stars (M ＞15 M⊙) evolve off the main sequence (MS), their helium core can ignite degenerately in a helium flash. Such stars then lose a significant amount of their mass due to strong stellar winds.Sometimes they even lose their entire outer envelopes during the phase of helium fusion. When this occurs, the helium-burning cores of such stars will be revealed before they become WDs or neutron stars.Such exposed helium-burning cores are known as HeMS stars(Hurley et al.2000),and can have temperatures reaching ＞50,000 K.Due to a lack of template spectra for hot stars, GalevNB adopts blackbody curves to approximate the SEDs of objects with temperatures above 50,000 K.The evolutionary path of an HeMS star depends on whether or not it is part of a binary system.

Figure 2. The SEDs of model 100 k-4Z. Colors and symbols are identical to those in Figure 1.

In all of our simulated clusters,HeMS stars sparkle mostly in the SED of binary systems during the first 50 Myr,and become the major contributors to the UV flux at young ages. They radiate in UV until the cluster reaches an age of a few hundred million years. HeMS stars that are part of a binary system continue to emit UV flux until t ≈1 Gyr, although their contribution to the UV-excess declines as the cluster ages. It should be noted, however, that the number of single HeMS stars in our models is much smaller than the number of HeMS binaries.This difference originates from the initial binary setup for our modeled clusters,for which massive stars preferentially reside in binary systems.

3.1.3. White Dwarfs

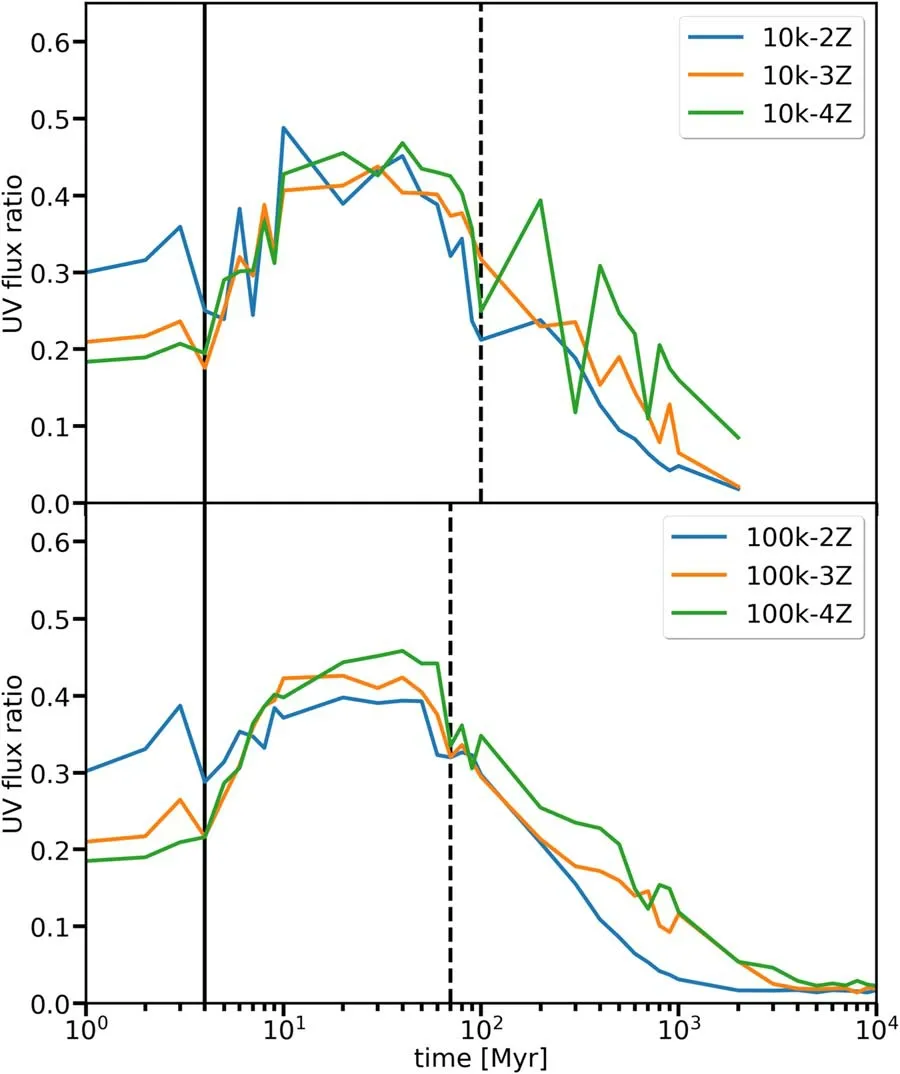
Figure 3. The evolution of the UV flux (from 1216 Å to 2500 Å) ratio with time. The upper and lower panels show the results for the 10 k and 100 k models,respectively.The vertical solid(4 Myr)and dashed(100 Myr:upper panel;70 Myr:lower panel)lines indicate two typical times when the UV ratio starts to increase and decline respectively.

WDs are long-term contributors to the UV-excess (orange,blue and light-green curves in panels(c)(1)–(4) of Figures 1 and 2).WDs are formed after the first 30–80 Myr in all models.WDs appear earlier in the metal-rich models, at 30–50 Myr,and appear at 80 Myr in the metal-poor models. Stars with masses of 8–10.5 M⊙will end up as oxygen-neon WDs(ONWDs, orange curve). Stars of intermediate mass will evolve into carbon-oxygen WDs (COWDs, blue curve). Lowmass stars are unable to fuse helium;such stars will evolve into helium WDs(HeWD,light green curve),and appear only after the cluster is a few hundred Myr old.

Young WDs are hot and blue (Mestel 1952; Torres et al.2014), and radiate a substantial fraction of their energy in the UV (＜2000 Å). COWDs dominate in the UV flux in the long run, while the ONWDs mainly contribute to the UV flux at younger ages. As the cluster ages beyond 1 Gyr, HeWDs become a major contributor to the UV flux. Although WDs eventually cool down, they are continuously being formed throughout the lifetime of the clusters. Therefore, the contribution of the WDs to the UV-excess for the star cluster is sustained over long timespans, and cannot be neglected.

3.2. UV Flux Ratio

To quantify the temporal evolution of the UV flux, we compute the UV flux of the UV-upturn from the Lyman break at 1216 Å to 2500 Å. We obtain the UV flux ratio by dividing the UV flux by the integrated flux of the entire cluster. The evolution of the UV flux ratio is presented in Figure 3.

Figure 4. The transmission curves of seven filters of CSST (indicated in the top-right corner of the figure), from UV to near-IR.

For cluster ages younger than roughly 4 Myr, the UV flux mainly originates from massive stars, and the UV flux ratio remains mostly constant in all models, with metal-rich models reaching high values. After 4 Myr (vertical black solid line),HeMS stars start to form, and become a major contributor to the UV flux. Therefore, the UV flux continues to increase. At about 10–20 Myr, the UV flux reaches a plateau. During the plateau period (which lasts about 70–80 Myr, between the vertical solid and dashed lines), WDs start to form and emit in the far-UV. Although WDs continue to form and emit UV radiation, they also gradually cool down. After ～70–100 Myr,the UV flux ratio declines, and the metal-poor models surpass the metal-rich models in UV brightness,since the luminosity of metal-poor WDs is brighter (Althaus et al. 2015).

Note that we have not included helium enrichment in the stellar evolution modeling. Observational studies have found that metal-rich clusters with helium enhancement can produce very blue stars, e.g., EHB stars (Lee et al. 2005).

4. Photometric Features

4.1. Color–Magnitude Diagrams

With the magnitudes produced by GalevNB, we obtain CSST and HST/STIS magnitudes for the simulated star clusters. The filter response curves of the CSST filters are presented in Figure 4. The color–magnitude diagrams (CMDs)for models 10 k-2Z and 100 k-4Z are displayed in Figures 5 and 6, respectively. CMDs of other models are presented in Appendix B. Crosses represent single stars, while circles correspond to binary systems. The HeMSs (red circles) are located to the left of the MS turn-off (MSTO). They occupy a region similar to the blue stragglers (BSs) or EHBs. Newlyborn ONWDs are particularly hot and blue (orange circles).Their magnitude is 5 mag fainter than the MSTO in the CSST g-band or HST F555W-band,but 3 mag bluer in NUV-g and 2–5 mag bluer in FUV-NUV.

Generally,the WD binaries are brighter than single WDs by several magnitudes. WD binaries are extremely blue at FUV-NUV until the end of the simulation. Before the first 1 Gyr,COWD+MS binaries are dominant among WD binaries.After 2 Gyr, helium WD+MS binaries start to populate, and become dominant in the population of WD binaries especially at very old ages (10 Gyr). When a WD has an MS companion of comparable mass,the binary is located between the MS and the WD sequence.Observations found accretion and outflow in several such binaries,which are known as cataclysmic variable(CV)stars.The MS companion in a CV typically has a spectral type ranging between G8 and M6, or is a brown dwarf companion (Warner 1995; Knigge et al. 2011). The MS and WD in a CV are typically separated by several solar radii. The donor star(the secondary)undergoes Roche-lobe overflow,and transfers material to the WD through the inner Lagrangian point. Note that the stellar evolution model implemented in PETAR is taken from Hurley et al. (2002); we do not model accretion disks.

Figure 5.The CMDs for the 10 k-2Z model.The filled colored circles signify binary systems,and the crosses represent single stars.Different symbol colors indicate different stellar types. The discontinuity of the MS at the low-mass end is due to the limited number of spectral templates in Lejeune et al. (1997) for effective temperatures below 3000 K.

4.2. Radial Color Gradients

Shu et al. (2021) identified a radial color gradient in the DRAGON simulations (Wang et al. 2016), with bluer colors toward the cluster center and redder colors in the outskirts.This is a result of dynamical mass segregation in the star cluster. In the million-particle DRAGON simulations, a color difference of 0.2 mag in CSST NUV-y and 0.1 mag in HST F330W-F814W has been observed (Shu et al. 2021).

We obtain the integrated color of the CSST NUV-y and HST/STIS FUV-NUV for stars in different concentric annuli in all models at 2 Gyr and 10 Gyr (i.e., at the end of the simulations). Since giant stars generate significant color fluctuations, we only include MS stars in the computation of integrated color of the clusters. In Figure 7, we display the dependence of the integrated color on the cluster-centric distance. To minimize statistical fluctuations, all bins contain an equal fraction (10%) of the total number of stars in the cluster. Considering that, observationally, it is difficult to determine distances for individual member stars in star clusters,we provide both 2D and 3D cluster-centric distances.

A positive color gradient is observed in all 10 k models at 2 Gyr, and in the 100 k models at both 2 Gyr and 10 Gyr in CSST NUV-y color,from the center up to 3–4 half-mass radii(rh; upper panels in Figure 7). This positive color gradient is similar to that found in the DRAGON simulations (Shu et al.2021).At 2 Gyr,the color gradient has a difference in NUV-y of 0.2–0.3 mag up to 3–4 rhin both the 10 k and the 100 k models.The color gradient steepens over time,and has a color difference in NUV-y of 0.3–0.5 mag at 10 Gyr. The steepening of the positive color gradient in older clusters directly reflects the mass segregation. During the relaxation process,massive stars sink to the cluster center while low-mass stars migrate to the outskirts, which has been observed in Galactic star clusters (e.g., Hillenbrand & Hartmann 1998;Pang et al.2013;Tang et al.2018).As a cluster grows older,its degree of mass segregation increases. This evolution in mass segregation has been observed in star clusters of different ages after the release of Gaia Data Release 2(DR2)(e.g.,Tang et al.2019; Pang et al. 2020; Bhattacharya et al. 2021; Pang et al.2021;Ye et al.2021).Therefore,the cluster center is bluer than its outer parts, with a higher fraction of high-mass stars.

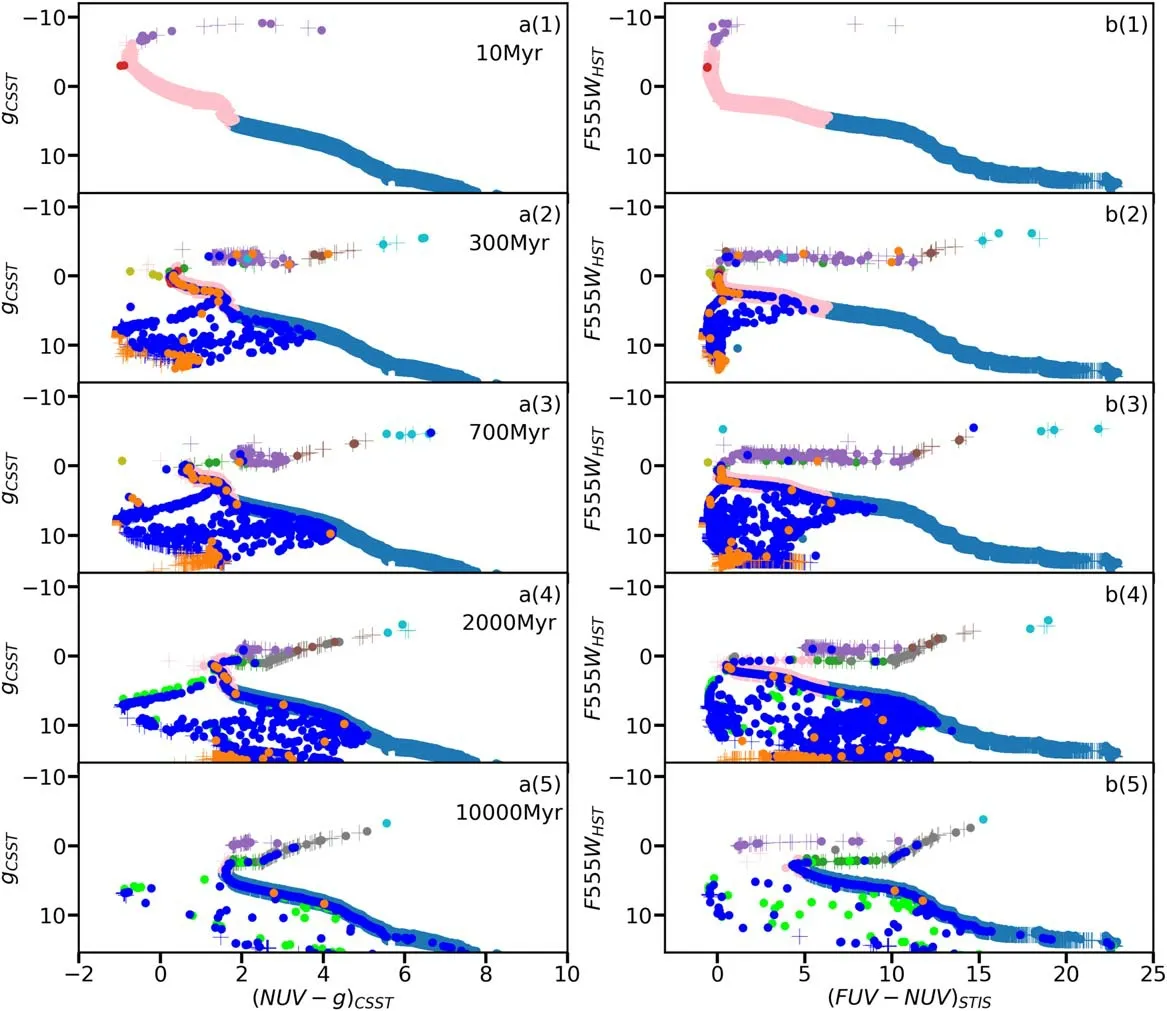
Figure 6. CMDs for the 100 k-4Z model. Symbols and colors are identical to those in Figure 5.

However, in HST FUV-NUV color (lower panels of Figure 7), the fluctuations are large, especially in the 100 k models.The FUV-NUV color is significantly affected by the presence of BSs that are more luminous and bluer than the MSTO. These are binary stars or stellar merger products. The BSs in our simulations are 2–3 mag bluer in FUV-NUV color and 3 mag brighter in the F555W band than the MSTO stars(see Figures 5 and 6).They generate a minor peak in the FUV spectra (Figure A4) and can be potential contributors to the UV-excess.There are more BSs in the 100 k models since they contain more binary stars,consistent with the observations that BSs are more numerous in higher-mass and older clusters(Jadhav & Subramaniam 2021).

When we additionally remove the BSs,the color gradient in FUV-NUV will be similar to that in NUV-y. Note that we exclude evolved stars in the integrated color derivation, which will elevate the color gradient.When all stellar populations are included, such as red giants, the color gradient suffers from large fluctuations.

5. Dynamical Evolution in the Star Clusters

5.1. Binary Evolution

Binary stars contribute to a large fraction of the UV flux in our simulations (see Sections 3 and 4.1). They are the major candidates for the origin of observed UV-excess in star clusters,especially WD binaries. Benefiting from direct N-body simulations, we are able to follow the dynamical evolution of each of the binary candidates that contribute to the UV-excess.

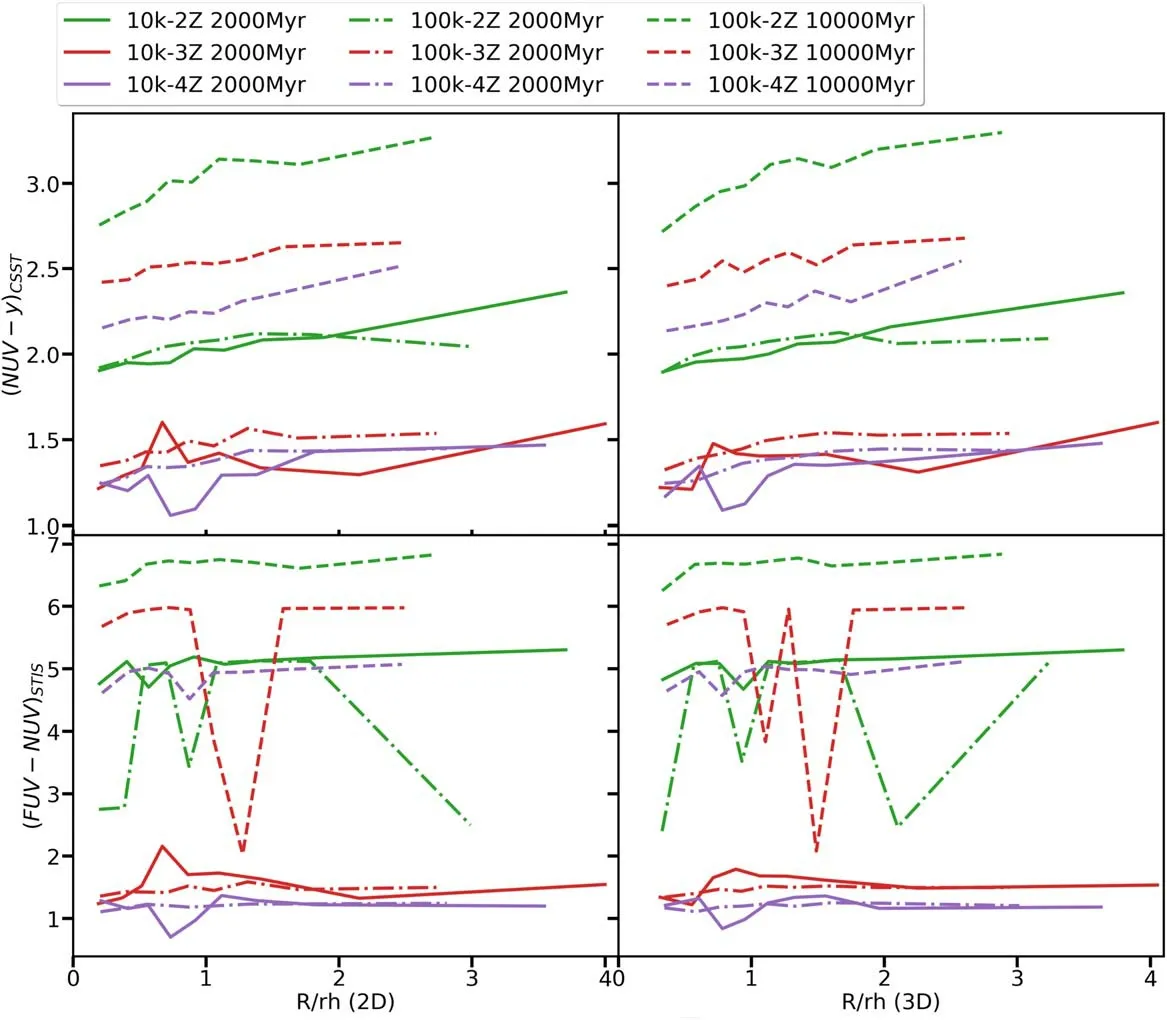
Figure 7.The dependence of the color NUV-y(CSST,upper panels)and FUV-NUV(HST/STIS,lower panels)on 2D and 3D cluster-centric distance(in units of the half-mass–radius) for all models. All bins contain 10 percent of the total number of stars in the cluster.

Binaries are strongly affected by the long-term dynamical processes in the star cluster.This process is faster with a higher local stellar density. Therefore, the fraction of binary stars in the cluster center will differ from that in the outskirts.We show the radial binary fraction in Figure 8.The radial binary fraction is computed as B/(S+B), where B is the number of binary systems, and S the number of single stars in each annulus. For all models,the binary fraction is initially uniformly assigned at all radii. During the first 100–200 Myr, the binary fraction drops in the center and increases toward the outer parts of the cluster. A large number of wide binary stars is disrupted as a consequence of stellar interactions in the dense cluster center,especially during the core collapse phase. The core collapse phase terminates at 100 Myr for the 10 k models and at 200 Myr for the 100 k models. According to the Heggie-Hills law (Heggie 1975; Hills 1975), wide binaries are easily disrupted during close encounters in the process of core collapse, while tight binaries tend to become tighter after interactions and can survive for long periods of time. The boundary between these wide and tight binaries (i.e., the critical semimajor axis) is determined by the local velocity dispersion. Consequently, a higher fraction of wide binaries is disrupted in the core than in the halo of a star cluster.

Subsequently, the radial binary fraction trend reverses. The binary fraction decreases significantly with increasing radius.This radially decreasing trend agrees with the results of the DRAGON simulations (Shu et al. 2021). The trend grows steeper with time and becomes most profound at the end of each simulation, which is consistent with observations of GCs(Milone et al. 2016).

5.2. Dynamical Features of WD Binaries

Figure 8.The evolution of the binary fraction along the radial direction for all six models.The binary fraction is computed as the fraction of binary systems among all stars(single+binary)in each annulus.Curves of different colors represent different ages,which are consistent with the SEDs(Figures 5 and 6,and B1,B2,B3,and B4) and the CMDs (Figures 1 and 6, and B1, B2, B3 and B4).

In the CMDs (Figures 5 and 6), WD binaries are outstandingly blue or UV, and are located between the MS and the WD sequence. Unfortunately, the accretion algorithm for binary stars of Hurley et al. (2002) may not be sufficiently accurate to model the mass-transfer processes in CV candidates. Instead, we identify CV candidates as a binary composed of a WD and an MS star. These are excellent candidate sources for the UV-excess in star clusters, consistent with the findings from our simulations in which WD binaries are a major contributor to the emitted UV radiation.We are motivated to investigate the dynamical evolution of the CV candidates.

Several studies have found that the luminosity function of CVs tends to be different for different GCs (Cohn et al. 2010;Rivera Sandoval et al. 2018; Lugger et al. 2017). The magnitude distributions of two GCs, NGC 6397 and NGC 6752, are bimodal (Cohn et al. 2010). Cohn et al. (2010)suggested that the optical emission of the bright group of CVs in NGC 6397 originates from the donor stars or accretion disks,and that of the fainter group originates from the WDs. The magnitude distribution of 47 Tuc, on the other hand, shows a unimodal distribution (Rivera Sandoval et al. 2018). There are fewer bright CVs in 47 Tuc per unit mass than in the other clusters. The cumulative radial distributions of bright CVs in both NGC 6752 and NGC 6397 manifest a strong concentration toward the cluster center, while the fainter CVs tend to be located at larger radii (Rivera Sandoval et al. 2018; Lugger et al. 2017).

In order to be able to compare our findings with observations, we analyze the gCSSTmagnitude and clustercentric distance for the CV candidates in our models (see Figure 9).We find that only within 2 Gyr,CV candidates have a bimodal distribution in gCSSTfor both the 10 k models and the 100 k models. There is a peak around gCSST～10 mag and another peak around gCSST～7 mag. Note that the magnitudes computed from the N-body models are absolute magnitudes.As the cluster grows older at 10 Gyr (100 k simulations), only the gCSST～10 mag is visible, with a plateau distribution at the bright region. We select bright CV candidates, i.e., those with magnitudes brighter than gCSST=7 mag (bright population,shaded histogram in the left-hand panels of Figure 9), and highlight the fraction of bright CVs among all CV candidates in the histogram of cluster-centric distance (middle panels of Figure 9).

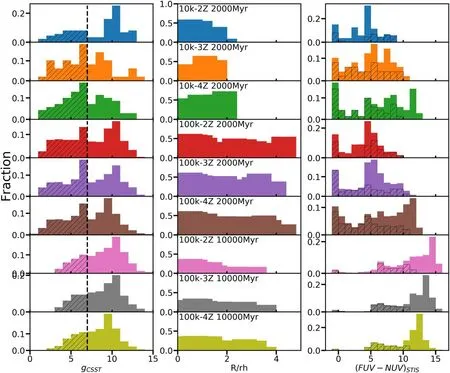
Figure 9. The properties of CV candidates at different cluster ages. The left-hand panels show the distribution of the gCSST magnitude of the CV candidates. The vertical dashed line highlights the brighter population of CV candidates(gCSST ≾7 mag;shaded histograms).The middle panels present the distribution of the fraction of bright CVs among all CVs in each annulus in the units of half-mass–radius rh. The right-hand panels are the histograms of FUV-NUV colors. The shaded histograms in the middle panels and right-hand panels correspond to the brighter population.

During the first 2 Gyr the fraction of bright CVs remains almost constant from the cluster center to the outskirts in all models. We do not observe a preference for the bright CVs to be located in the cluster center at this stage. When the clusters grow as old as 10 Gyr, the fraction of bright CVs in the center is marginally higher than in the outskirts. This trend is most pronounced in the 100 k-2Z model. Although bright CV candidates do not show a spatial preference, they are indeed much brighter in FUV-NUV(right-hand panels of Figure 9),and mainly occupy the peak at FUV-NUV=0 mag. At 10 Gyr, the bright CV candidates are solely brighter in FUV-NUV, compared to the faint population.

These bright CV candidates are COWD and HeWD binaries(see Figures 5 and 6).This may be an evolutionary effect. The progenitors of COWD and HeWD are intermediate-mass and low-mass MS stars. They require a longer time than highermass stars to experience mass segregation, since the mass segregation timescale is inversely proportional to stellar mass(e.g.,Pang et al.2013).At 2 Gyr,these MS stars are segregated into the cluster center and finally become WDs. As the cluster grows older, the brightness of COWD or HeWD declines and dynamically diffuses to larger radii as a consequence of interactions with neighboring single stars or binaries. Hence,the old CV candidates show no peak at the bright magnitude or in cluster-centric distance.Finally,the bright CV candidates are a major source of FUV radiation in the cluster.

Figure 10. Color–color diagrams in HST/STIS color: (Top) FUV-V vs. V-I;(Middle) FUV-NUV vs. V-I;(Bottom) NUV-V vs. V-I. Only the 100 k models are presented.The simulation starts at the diamond(0 Myr)and ends at the filled circles(10 Gyr).Star-symbols are observed GCs in the MW(red)and in M87(purple and brown). The purple stars are GCs with both FUV and NUV observations, while the brown stars only have FUV observations.

Therefore,the location of bright CV candidates closer to the cluster center may be due to internal dynamical evolution of the cluster. However, we cannot exclude that their brightness may originate from mass transfer between CV components, as suggested in earlier observational studies (Rivera Sandoval et al. 2018; Lugger et al. 2017). Limited by the binary evolution model in PETAR, detailed simulation of CV candidates with realistic analytical models in a star cluster environment is necessary in the future.

6. Discussion

6.1. Comparison to Observations

To verify the consistency of our models with observations,we compare the UV photometric features of our 100 k models to those of GCs in M87 and in the MW.Note that the 100 k models only reach the lower-mass limit of GCs. Sohn et al. (2006)observed UV-bright stars in old, metal-rich GCs in the giant elliptical galaxy M87 with HST/STIS FUV and NUV photometry. Sohn et al. (2006) recomputed the UV photometry of the MW GC samples from Dorman et al.(1995)with the metallicity[Fe/H] and reddening E(B-V) from Harris (1996). We adopt the photometry in Tables 3 and 4 from Sohn et al.(2006)for M87 and that of Table 6 from Sohn et al. (2006) for MW GCs.

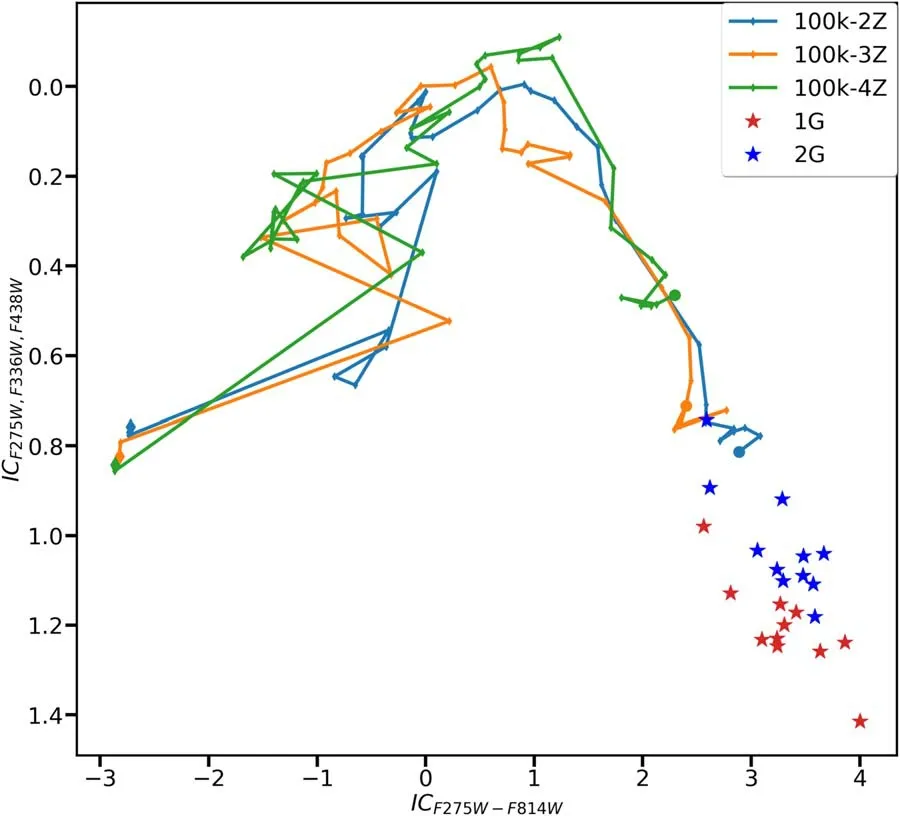
Figure 11.ICF275W,F336W,F438W versus ICF275W-F814W integrated two-color diagram for 100 k models.Data for the eleven GCs(star symbols)are obtained from Jang et al. (2021). The red stars represent the population of first generation stars in the GCs, and the blue stars represent the second generation.

In Figure 10 we displace the color–color evolution of the 100 k models, starting from a diamond symbol. At the end the simulations (filled circles), the FUV-V color of our models only matches the bluest GCs in M87. However, our models are bluer than all MW GC samples. The V-I of the models agrees with the observed GCs in both galaxies.The 100 k-2Z and 100 k-3Z model overall is consistent with the FUV-NUV color of MW GCs. The FUV-NUV color of GCs in M87 is about 1–2 mag bluer than the model predicted at 12 Gyr. All three models predict a bluer NUV-V color(1 mag brighter),than the observed GCs. GCs in M87 are 0.5–1 mag brighter in FUV and NUV photometry than those in the MW. Since the metallicity in M87 is super-solar, helium enhancement is suggested to be a promising mechanism to explain the UV-excess in their GCs(Sohn et al.2006).However,in our simulation,we cannot modify the helium abundance in the stellar evolution models,which thus may induce the observed discrepancy in Figure 10.

Jang et al. (2021) separated the first and second generation of stars in eleven GCs using the (mF336W–mF438Wversus mF275W–mF336W) color–color diagram. Their results show that the integrated color of the second generation stars with helium enrichment is bluer in the color ICF275W,F336W,F814W(Milone et al.2015)than the first generation stars.We display the evolutionary tracks of the three 100 k models in Figure 11.At an age of 12 Gyr,the simulated clusters match the integrated color ICF275W,F336W,F814Wand ICF275W,F814Wat the bluest part of the second generation stars (blue stars in Figure 11), but are about 0.2–0.4 mag bluer than the first generation stars (red stars in Figure 11)in ICF275W,F336W,F814W.Note that all our models have a lower metallicity than the eleven observed GCs analyzed in Jang et al. (2021). Therefore, we predict a bluer color, even for first generation stars.

6.2. Predictions for Future CSST Observations

To observe the UV-excess in a star cluster,the FUV filter is the best wavelength to cover the UV-upturn region.The NUV band in CSST goes down to 2500 Å,where the UV-upturn SED just starts to rise toward shorter wavelength. Therefore, the ability and sensitivity of CSST photometry in detecting UV-excess in a star cluster need to be tested. We present the correlation between the FUV-NUV color of HST/STIS and NUV-g of CSST in Figure 12. Different colored curves represent different models.The simulated clusters begin at the lower left of the figure(diamond symbols) and evolve to the upper right corner (filled circles,end of the simulation).We fit the correlation between HST and CSST colors with a parabola, coefficients of which are displayed in the upper left corner in each panel. The correlation has a larger scatter in NUV-i and NUV-y than in NUV-g.Therefore,we suggest that NUV-g is the best color to search for a correlation with HST/STIS FUV-NUV.

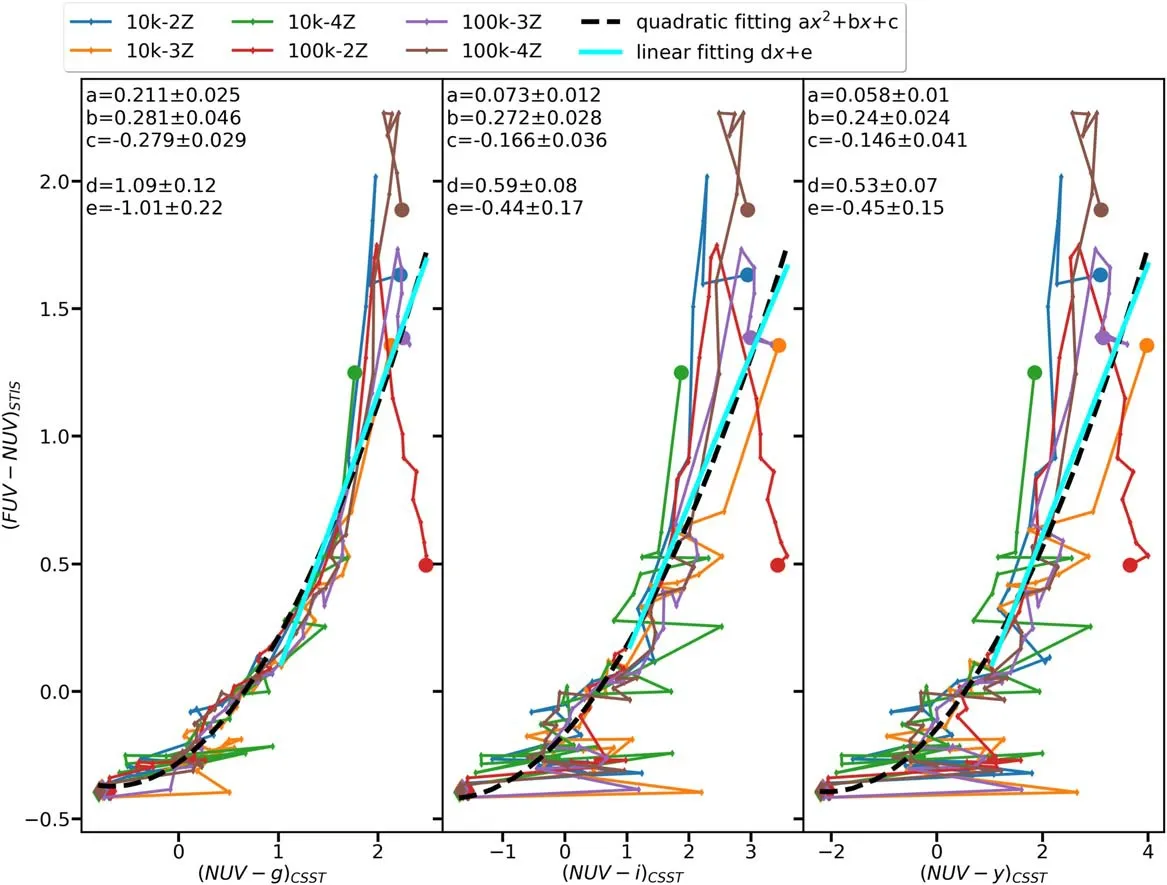
Figure 12. Correlation between FUV-NUV (HST/STIS) and NUV-g (CSST) for all models. The dashed black curve is a least squares fit to all simulated data points.Each point represents one snapshot of the simulation.The simulation starts at the diamond(0 Myr)and ends at the filled circles(2 Gyr for the 10 k models and 10 Gyr for the 100 k models).

At colors bluer than NUV-g=1 mag,the CSST NUV-g is not sensitive to HST FUV-NUV. The slope of the parabola in this range is very shallow. When the color is redder than NUV-g=1 mag, the correlation between FUV-NUV and NUV-g becomes steeper and close to a linear relation, with a slope of 1.09±0.12.We can use the correlation to convert future observed CSST NUV-g into HST/STIS FUV-NUV. At NUV-g=1 mag, it corresponds to 200 Myr in simulations.

Therefore, the best observational color to detect UV-excess in star clusters for the future CSST observation lies in NUV-g ＞1 mag. In this color range, we can convert the observed integrated cluster color NUV-g into HST/STIS color FUV-NUV via the linear correlation

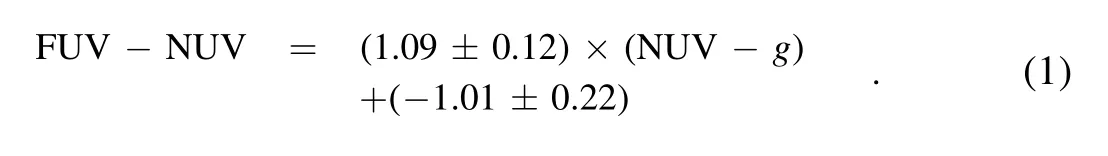
We suggest that the best target clusters to look for the signature of UV-excess or UV-upturn via CSST are clusters older than 200 Myr.

7. Summary

We evolve a set of six N-body models of star clusters using PETAR code, with different particle numbers (N = 10 k and N = 100 k) and different metallicities (Z = 0.01, 0.001, and 0.0001). We adopt simple stellar populations; we do not include multiple stellar populations, and we do not include helium variations in the N-body models. Using the GalevNB package,we convert the physical stellar properties generated by PETAR into SEDs,spanning the far-UV to the near-IR,and into photometric CSST and HST magnitudes. By observing the long-term evolution of the photometric and spectral features of the simulated clusters, we identify the stars that produce the UV-excess/UV-upturn feature in the star clusters’ SEDs at wavelengths between 1216 Å and 2500 Å.We also analyze the dynamical evolution of UV-excess candidate stars: WD+MS binaries. The main objective of our study is to predict the observational features of star clusters for future CSST observations and identify the sensitivity and ability of the CSST in detecting UV-excess in star clusters.Our main results can be summarized as follows.

(1) Three types of stars are identified as candidates for UVexcess candidates in star clusters: SAGBs, naked helium stars and WDs. Among these, SAGBs are present in the star cluster at young ages. Due to the short lifetime of SAGBs, their contribution to the UV-excess is not significant. On the other hand, naked helium stars continue to radiate in the FUV until t ≈2 Gyr in the massive cluster models (100 k). In the long term, the greatest contributors to the UV-excess are the three types of WDs: ONWDs, COWDs and HeWDs.

(2) The UV flux ratio (i.e., the ratio between the UV flux in the wavelength range 1216–2500 Å divided by the total flux of the cluster) in the SEDs of the six models reaches a plateau period from 10 to 80 Myr. During the plateau phase, the UV flux is mainly produced by the hot and blue naked helium stars and by young WDs.

(3)A color gradient with a CSST NUV-y color difference of 0.2–0.5 mag within 3–4 rhis observed in all models. The color gradient becomes more pronounced in the 100 k models as the clusters age from 2 Gyr to 10 Gyr.This is expected from mass segregation due to dynamical relaxation. On the other hand, no color gradient is found in the HST/STIS FUV-NUV color. Large fluctuations in FUV-NUV are induced by BSs.

(4) Soft binary systems are rapidly disrupted in the dense core region of a cluster, especially during the core collapse phase.Therefore,the radial binary fraction declines toward the cluster center within the first 100 Myr and 200 Myr for the 10 k and 100 k models, respectively. After the termination of the core collapse phase,two-body relaxation dominates the internal dynamical processes. The binary fraction increases toward the cluster center, as the process of mass segregation continues.

(5)We select the WD+MS binaries as the CV candidates.At an age of 2 Gyr, there is clear evidence of a bimodal distribution in the gCSSTmagnitude distribution of CV candidates. We do not observe a significant spatial preference for the bright population of the CV candidates during the first 2 Gyr. They become marginally centrally concentrated at 10 Gyr, especially for the 100 k-2Z model. The bright CV candidates are also especially bright in FUV-NUV and are major contributors to the UV-excess features in the cluster. At the end of the simulation of the 100 k models at t=10 Gyr,the bright CV population fades out and their magnitude distribution becomes unimodal.

(6)By comparing the HST/STIS color of UV-excess GCs in M87 and in the MW, we find that our models agree with observations in V-I. The FUV-V color matches the M87 GCs,but is bluer by 0.5 mag than the MW GCs.The NUV-V is also bluer than all GC samples by ～1 mag. On the other hand, the FUV-NUV color is redder than that of observed GCs by up to 1–2 mag.This discrepancy may originate from a different helium abundance in these GC populations. In order to tackle this problem, additional numerical simulations with varying helium abundances in the stellar evolution are required.

(7) The CSST NUV-g color is most sensitive to HST/STIS FUV-NUV in the color range NUV-g ＞1 mag. We find a strong correlation between the CSST NUV-g color and HST/STIS FUV-NUV with our models. Especially after the cluster grows older than 200 Myr,this correlation approaches a linear relation: FUV-NUV=(1.09±0.12)·(NUV-g)+(-1.01±0.22). For future CSST observations of extragalactic star clusters, this linear correlation may provide an essential relation that allows conversion of NUV-g colors into FUV-NUV colors, and can help to further unravel the origins of the observed UV-excess in star clusters.

Acknowledgments

We thank the anonymous referee for advice to improve the paper.We give thanks to Prof.Chengyuan Li from Sun Yat-sen University for providing helpful comments on multiple populations. We are grateful to Ms. Han Qu for computing the zero-points for all filters of CSST. We acknowledge the science research grants from the China Manned Space Project with No. CMS-CSST-2021-A08. X.Y.P. is grateful for the financial support of the National Natural Science Foundation of China (NSFC, Grant No. 12173029), and the Research Development Fund of Xi’an Jiaotong-Liverpool University(RDF-18–02–32). L.W. thanks the support from the onehundred-talent project of Sun Yat-sen University and the National Natural Science Foundation of China (NSFC, Grant No. 12073090) and financial support from JSPS International Research Fellow (Graduate School of Science, The University of Tokyo). M.B.N.K. acknowledges support from Research Development Fund project RDF-SP-93 of Xi’an Jiaotong-Liverpool University.

Appendix A Spectral Energy Distribution

We provide the SEDs for models of 10 k-3Z, 10 k-4Z, 100 k-2Z and 100 k-3Z in this section. Panels (a)(1)–(4) of Figures A1,A2,A3 and A4 are integrated SEDs for the whole cluster(dotted blue curve),in which the SED of single(orange curve) and binary (green curve) stars are specified. Panels (b)(1)–(4) and (c)(1)–(4) present the SED of different spectraltypes (see Figure 1) in single and binary stars, respectively.

Figure A1.The SEDs of model 10 k-3Z.(a)(1)–(4)The SEDs for the entire star cluster(dotted blue curve),the single stars(solid orange curve)and the binary systems(solid green curve). (b)(1)–(4), (c)(1)–(4) The SEDs for individual populations of single stars and binary systems, respectively, in which we highlight the SEDs for different SPs with different color curves. The list of abbreviations for the SPs is provided in Table 2. Symbols and colors are identical to those in Figure 1.

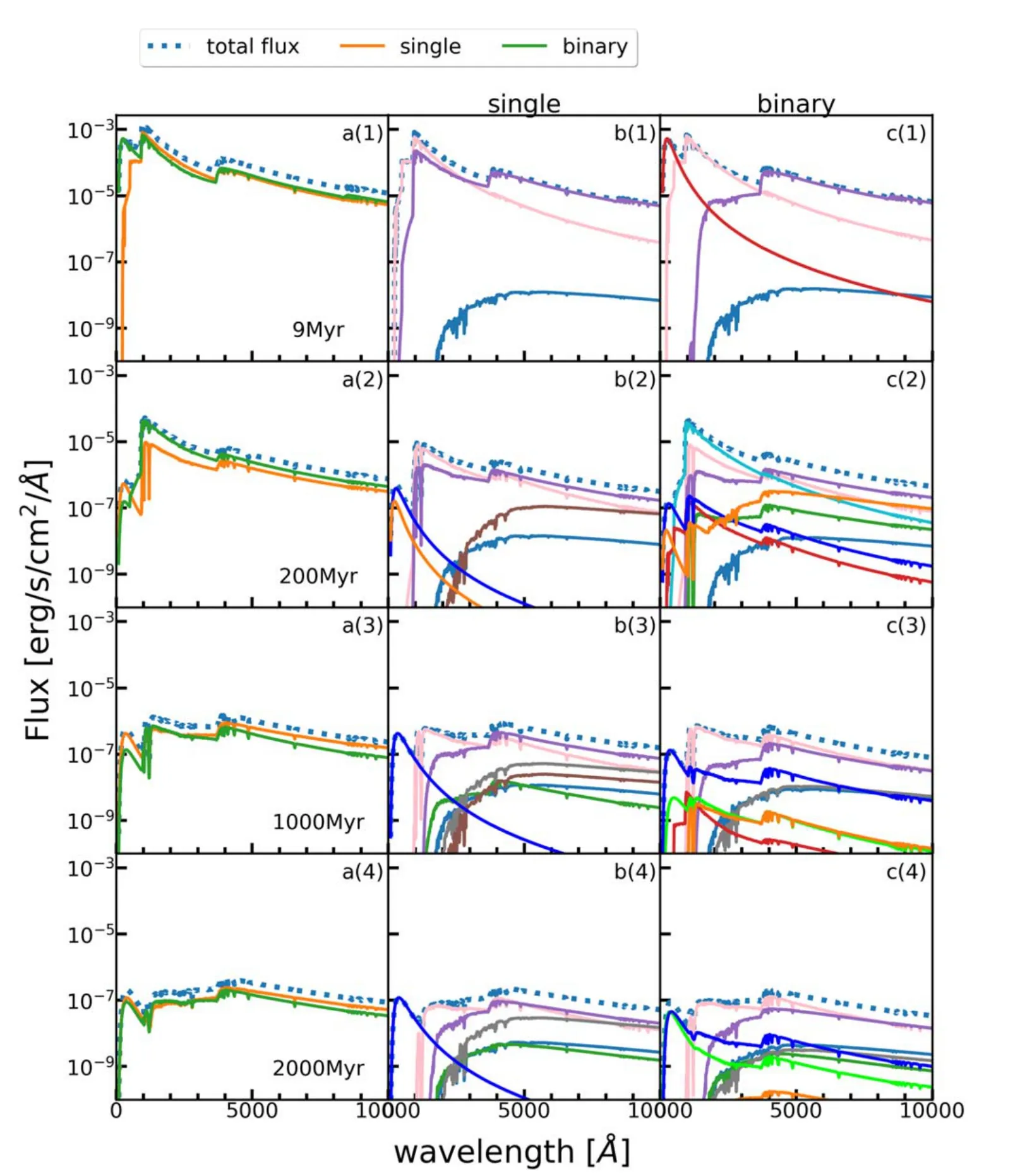
Figure A2. The SEDs for model 10 k-4Z. Symbols and colors are identical to those in Figure 1.

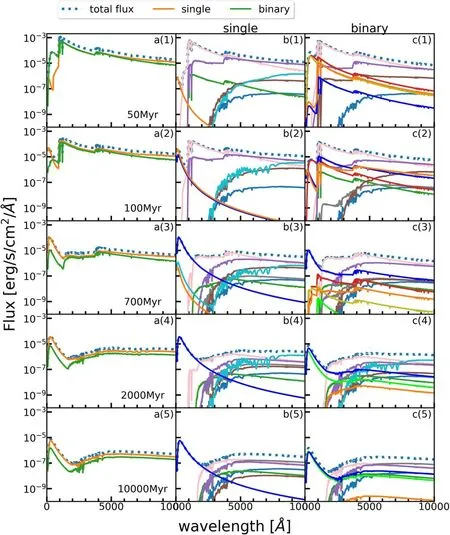
Figure A3. The SEDs for model 100 k-2Z. Symbols and colors are identical to those in Figure 1.

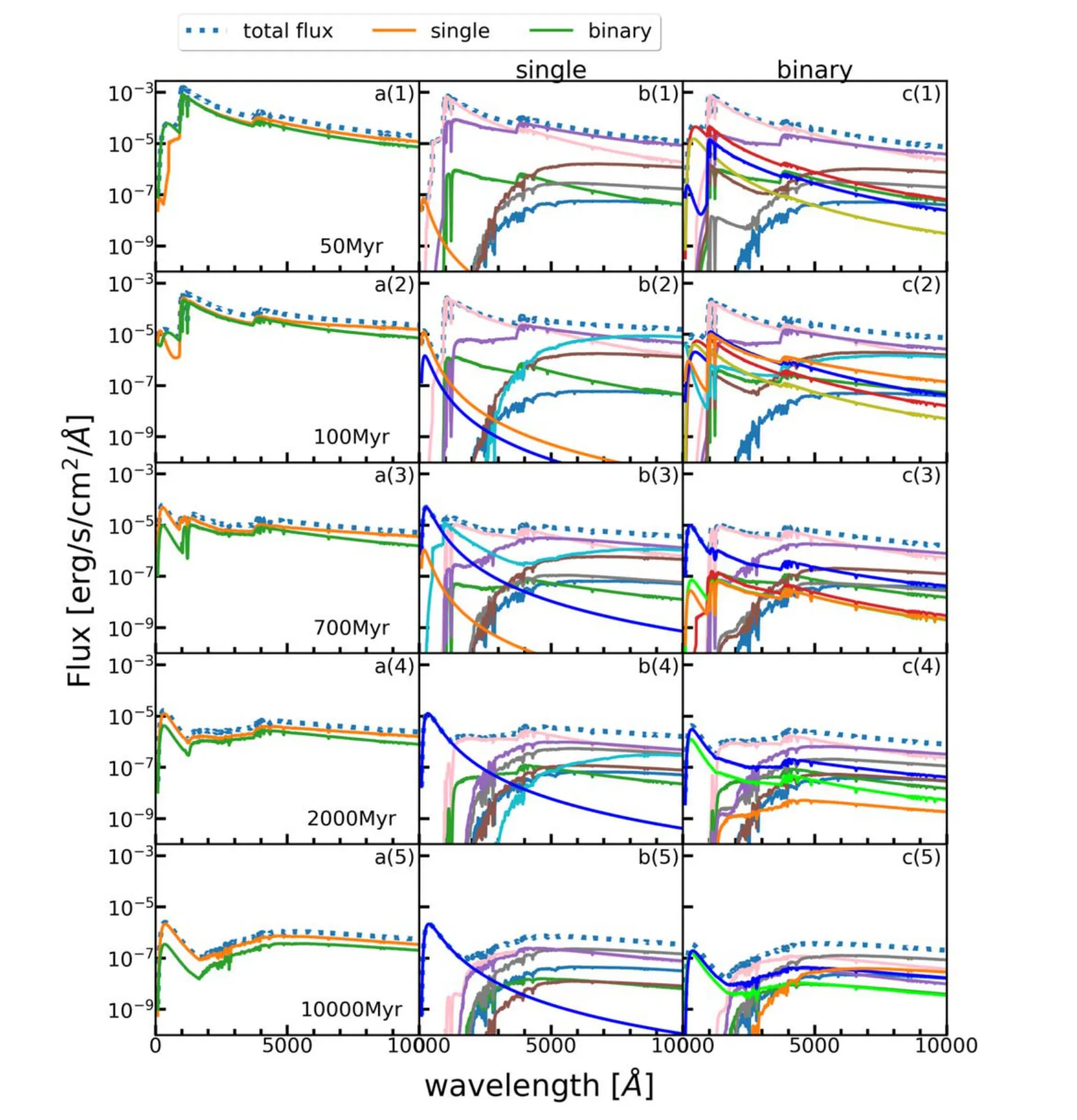
Figure A4. The SEDs for model 100 k-3Z. Symbols and colors are identical to those in Figure 1.

Appendix B Color Magnitude Diagrams

CMD for models 10 k-3Z,10 k-4Z,100 k-2Z and 100 k-3Z are displayed in this section. The circles indicate binary stars,while the plus symbols single stars. The color of symbols denotes different spectral-types(see Figure 4). Panels(a)(1)–(4)and (b)(1)–(4) in Figures B1, B2, B3 and B4 are CMD at different ages in CSST and HST photometry, respectively.

Figure B1.The CMDs for model 10 k-3Z.The filled colored circles signify binary stars and the crosses mark single stars.Different symbol colors represent different stellar types.The discontinuity of the MS at the low-mass end is due to a smaller number of spectral templates in Lejeune et al.(1997)for effective temperature below 3000 K.

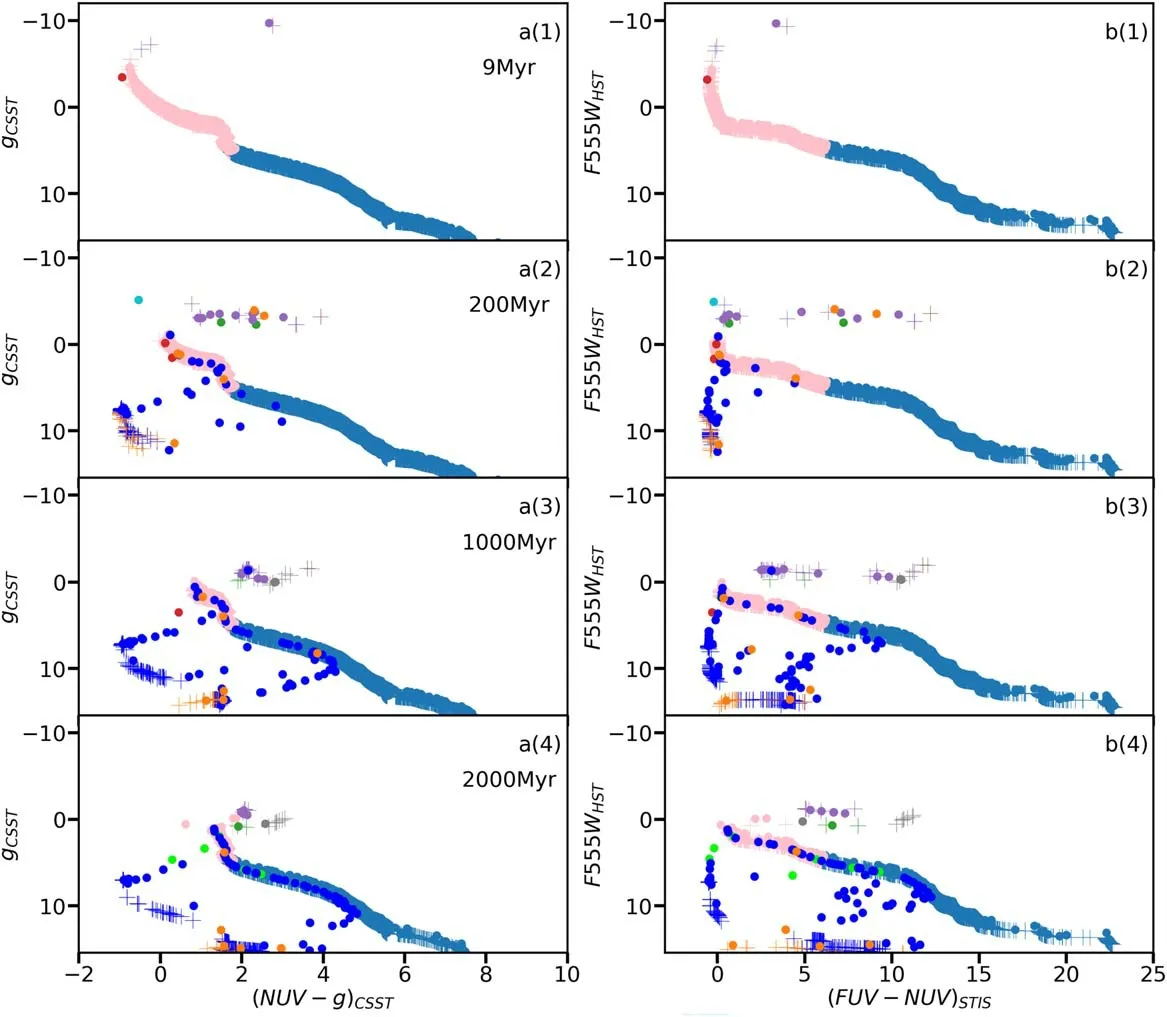
Figure B2. The CMDs for model 10 k-4Z. Symbols and colors are identical to those in Figure 5.

Figure B3. The CMD for model 100 k-2Z. Symbols and colors are identical to those in Figure 5.

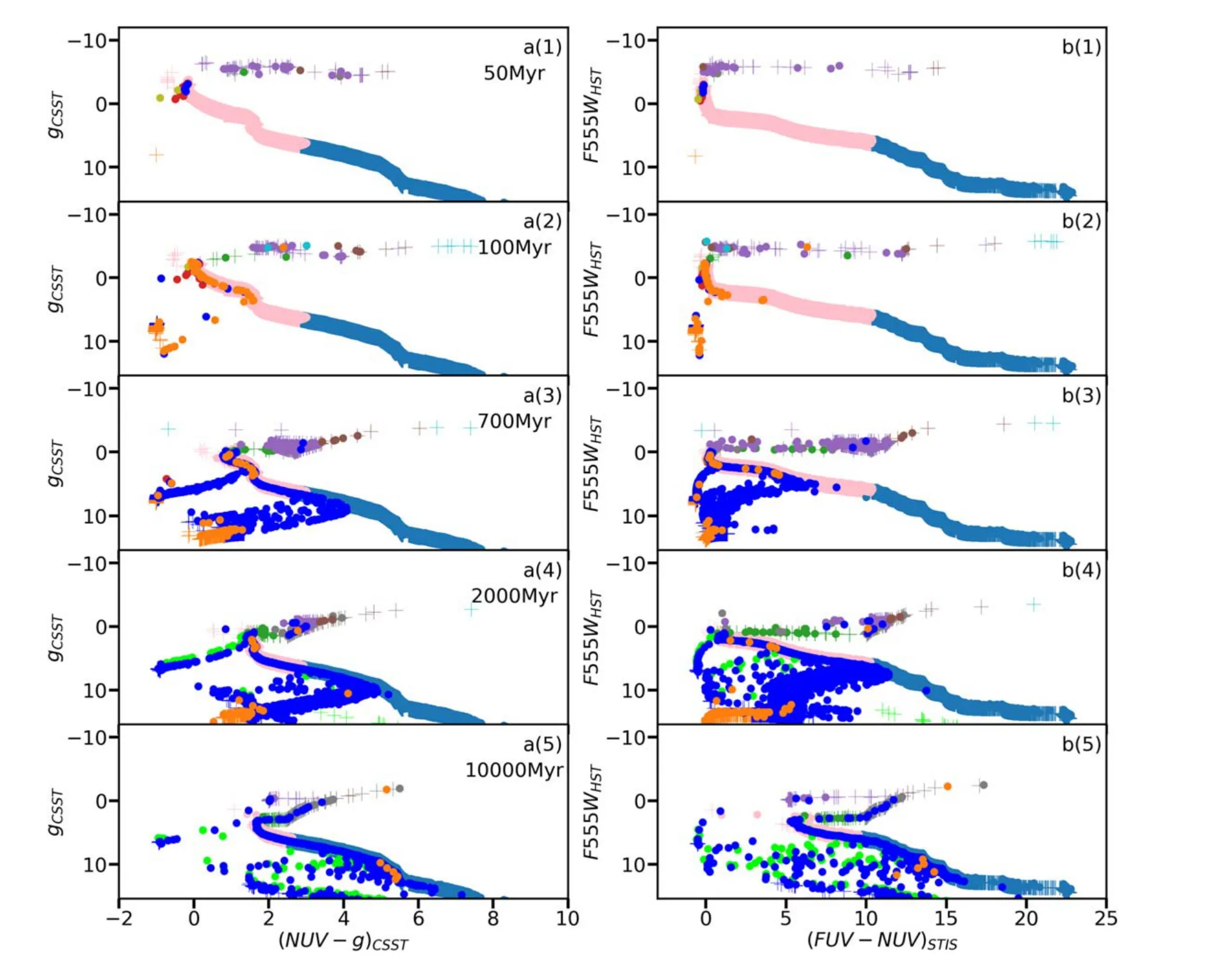
Figure B4. The CMDs for model 100 k-3Z. Symbols and colors are identical to those in Figure 5.

ORCID iDs

Xiaoying Pang https://orcid.org/0000-0003-3389-2263 Long Wang https://orcid.org/0000-0001-8713-0366 M. B. N. Kouwenhoven https://orcid.org/0000-0002-1805-0570