棒束弯曲对子通道内空气 - 水两相流动的影响研究

李潘潇，孙 皖，周文雄，马在勇，张卢腾，潘良明

（重庆大学 低品位能源利用技术及系统教育部重点实验室，重庆 400044）

在反应堆运行过程中，因受到辐照变形、机械振动、热应力等影响，反应堆燃料棒束可能发生变形弯曲导致子通道形状的改变。这可能对冷却剂的流动换热产生不利影响，威胁反应堆的安全运行。因此，深刻理解棒束弯曲子通道在相态特性分布和流动特性演化方面的机制对反应堆的安全设计与分析具有重要意义。

目前对于棒弯曲子通道热工水力特性的研究主要是通过实验进行的，自1975 年以来，多位科学家对不同燃料棒束子通道内的热工水力进行了实验研究，实验结果被用于燃料组件的安全评估。如1975 年K.W.HILL 和F.E.MOTLEY等人对4 × 4 棒束燃料组件展开实验研究[4]；1977 年E.S.MARKOWSKI 等发表了关于C-E型压水堆燃料组件棒束弯曲对CHF 的实验研究结果[2]；2004 年中国核电研究所（NPIC）用CHF实验测量了在冷壁套管微元和典型微元中不同间隙闭合的棒束弯曲的影响[1]。实验研究发现棒束弯曲在高压高热流密度时会对CHF 产生影响，同时间隙闭合度高于 50%时棒束弯曲对CHF 的影响较大。然而实验研究对于微观测量空泡份额的变化及气泡运动速度的难度较大，捕捉不到气泡的演化过程，而计算流体动力学（CFD）为微观层面的认识提供了有力工具。因此，为了研究棒弯曲对子通道内流动特性与气泡演化的影响。本文基于Fluent 软件，采用VOF 模型，利用非稳态、隐式分离求解算法进行模拟计算，数值研究了不同含气率下棒弯曲程度对棒束子通道内空气 - 水流动相态分布的影响。不互相混合的前提下。在VOF 模型中，不同的流体组分共用着一套动量方程通过引进相体积分数这一变量，实现对每一个计算单元相界面的追踪。在每个控制容积内，所有相的体积分数之和为1。在两相流动计算中，若液相的体积分数为α，则可能存在以下三种情况：α= 1控制体内被液相充满；α= 0，控制体被气相充满；0＜α＜1，控制体内包含两相流界面。

基于α的值，适当的属性和变量在一定范围内分配给每一个控制单元。

体积分数方程跟踪相之间的界面是通过求解一相或多相的容积比率的体积分数方程（连续性方程）来完成的。对于液相，方程如下

式中：mlg——气相到液相的质量输送；

mgl——液相到气相的质量输送。

1.1 两相界面流体属性

存在于每一控制容积的分相决定出现在输运方程中的两相流界面属性。在两相流系统中，液相用下标l表示，气相用下标g表示，如果液相的容积比率被追踪，那么每一单元中的密度由下式给出：

通常对于两相系统，容积比例平均密度采用加权平均的方式给出：

1 数学模型

VOF 模型[11]是建立在固定的欧拉网格下的表面跟踪办法，建立在两种或多种流体（或相）

所有其他属性（如粘度）都以这种方式计算。

1.2 动量方程

通过求解整个区域内的单一的动量方程，作为结果的速度场由各相共享。两相密度ρ和粘度μ的属性，即各相的体积分数决定动量方程的求解。

1.3 表面张力

对于棒束弯曲子通道内的两相流动系统，表面张力不可忽略。Brackbill 等[8]在1992 年提出了连续表面力模型。在计算过程中，附加的表面张力增加到动量方程中源项上，如下式

式中：ρ——平均密度；

σlg——表面张力系数。

2 几何模型及网格划分

本文研究所采用的几何流道包括直棒及三种不同弯曲程度弯棒形成的2×2 棒束子通道共四种通道结构：正常子通道、50%闭合度子通道、80%闭合度子通道以及完全接触的情况。单棒直径为9.5 mm，棒间距12.6 mm，子通道全长400 mm，弯曲部分长度为250 mm，弯区段距离流道出入口75 mm。

对于不同弯曲程度的子通道，其网格划分方式不尽相同，有着些许调整，为了保证计算的质量，均采用了结构化的划分方法，网格划分采用L 型拓扑结构，图1 给出了不同闭合度子通道的最大弯曲截面上网格节点。在计算过程中发现，当网格的最小尺寸低于1×10-5m 时计算极易发生离散，其可能原因是网格的延伸比较大。故在不同弯曲程度的子通道模型网格划分时均保证了其有较好的膨胀比与延伸比，同时，并在壁面出进行了边界层加密，控制第一层网格y+值在1.3 左右。根据网格无关性测试，各个模型的网格数量控制在60 万～100 万间能满足计算的收敛性及准确性。具体参数及网格划分情况如表1 所示。

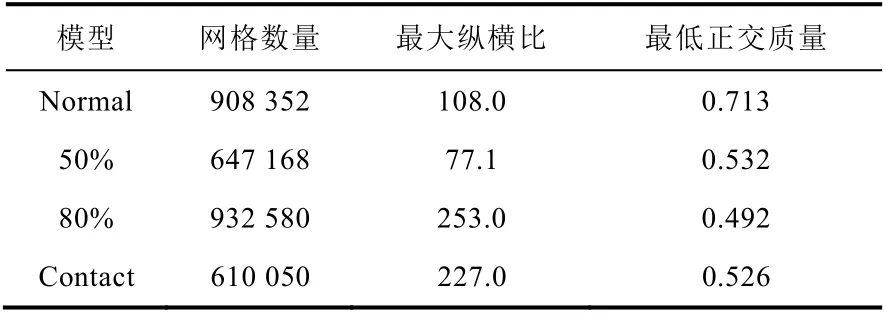
表1 网格划分信息Table 1 The mesh division information

3 计算方法及边界条件

对于棒束弯曲子通道模型模拟空气 - 水两相流动，空气、水两相可视为不可压缩、等温、定常物性的流体。其中ρair= 1.225 kg/m3，μair= 1.789 4×10-5Pa·s ；ρwat= 998.2 kg/m3，μwat= 1.000 3×10-3Pa·s。水的表面张力σ为0.07 N/m。进一步选择了瞬态VOF 模型对两相之间的流动过程进行模拟计算。同时考虑到湍流两相间的扰动、子通道模型的高曲率及壁面无加热等其它条件，故选择标准壁面的RNGk-ε模型进行湍流模拟。在求解方法中利用SIMPLIC 方法耦合流场压力及速度，使用PRESTO！方式离散压力，体积分数方程采用隐式时间格式离散求解。相间界面采用分段线性界面重构（PLIC）追踪，使两相界面更为精细。动量方程、湍流动能方程和湍流耗散率方程利用二阶迎风格式离散，以保证计算得精准性。考虑计算成本及计算精度，时间步长选择0.000 1 s，既保证计算能够平稳的收敛满足了模拟的可靠性，又使得计算时间不至于过长，且每隔0.02 s 数据进行保存一次。

边界条件：设置入口边界条件为速度入口边界，两相流速设置为1.2 m/s；研究了两种入口含气率（0.1 和0.5）的工况；出口设定为压力出口，无回流；设定入口及出口的湍流模型参数，水力直径根据几何结构尺寸计算为11.78 mm，湍流强度设为4.85%；4 个圆弧壁面均设为无滑移壁面条件；其余面设置为对称边界条件。

4 数值模拟结果及分析

本文计算了不同含气率、不同弯曲程度棒束子通道的两相流动，共12 个算例，计算了0.5 s 内通道的流动情况，计算发现当0.22 s 后通道内的流动相对比较稳定，空泡的演变也比较规则。

为了验证模型的有效性，基于我们开发的5×5 棒束空气 - 水两相流动实验数据拟合得到的两相摩擦压降模型[12]，通过对比模拟的总压降与模型计算的总压降来验证模型的有效性。如表2 所示，对于入口含气率为0.1 和0.5 的工况，其模拟的总压降相对偏差在20%以内，具有较好的吻合性。

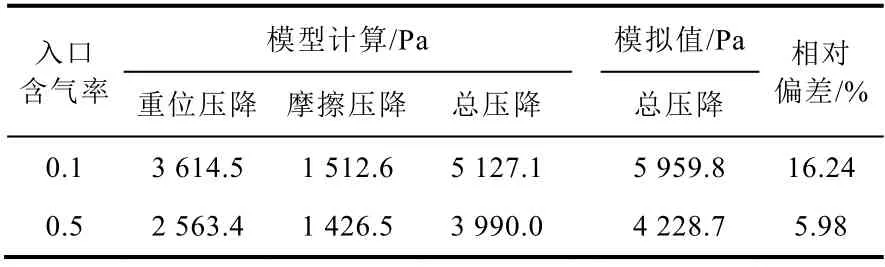
表2 模型有效性验证Table 2 The validation of the model

4.1 子通道内平均空泡份额

棒束弯曲必然使得冷却剂流道变窄，子通道内平均空泡份额可能会受到一定的影响。而平均空泡份额的变化往往反映了冷却剂流动结构的变化。为了研究棒束弯曲对子通道内空泡份额的影响，本文在子通道模型上选择三个轴向横截面，分别位于棒弯曲最大处、棒弯曲最大截面上游130 mm 处及棒弯曲最大截面下游130 mm 处。

（1） 含气率 = 0.1

入口含气率为0.1 时各截面的平均空泡份额随时间变化曲线如图2 所示。观察截面平均空泡份额沿轴向的变化，在棒束通道入口附近区域［见图2（a）］，由于空气和水以均匀混合的方式进入，此时截面平均空泡份额波动较小；而随着流动发展，小气泡逐渐聚合成为大气泡，大气泡流经所监测截面时，受气泡截面面积变化较大的影响，截面平均空泡份额呈现出现较大的波动［见图2（b）和（c）］。

观察含气率 = 0.1 时各截面的平均空泡份额随时间变化曲线，发现不同弯曲程度子通道在弯曲段中部截面上的平均含气率峰值较为接近，但80%闭合度子通道在弯曲段出口截面的含气率峰值相对较低，即棒束弯曲程度较大时，流道内气泡的体积会相对较小，但其流速也相对较快。

（2） 含气率 = 0.5

入口含气率为0.5 时各截面的平均空泡份额随时间变化曲线如图3 所示。观察截面平均空泡份额沿轴向的变化，与含气率为0.1 时工况具有同样的变化趋势，但由于空泡份额增大，入口处均匀的小气泡较早地发生聚合成为大气泡，因此在最大截面上游130 mm 仍观测到较大的截面平均空泡份额波动。观察含气率 = 0.5时各截面的平均空泡份额随时间变化曲线，发现闭合度较大的子通道的空泡份额与闭合度较小的子通道的空泡份额之间并没有较大差距，其峰值较为近似，但由于闭合度高的子通道截面面积相对较小，因此其内部的气弹体积也相对较小。

4.2 棒弯曲对空泡演化的影响

如图4 为入口含气率为0.1 时子通道内流型近似泡状流。气相向流道中心聚集，形成近似圆柱体，头部偏球形的较大气泡。同时在四个流道分支上也观察到连续的体积相对较小的气泡。随着闭合度的不断增加，流道中心气泡在径向受到压迫从而在轴向产生一定的延伸。弯曲段附近流道分支上的气泡数目增加，其与流道中心气泡结合的概率也有所增加。随着闭合度的不断增加，弯曲段内气泡间的距离逐渐增大，其主要原因是弯曲段入口对气泡有一定的加速作用，且闭合度大的子通道加速作用更明显，因此弯曲段内气泡的速度相对较快。

如图5 所示为入口含气率为0.5 时子通道内流型近似弹状流，四个圆弧壁面处，气弹周围的液膜被撕破，许多流道分支内的气泡与流道中心的气泡结合。随着闭合度的不断增大，流道中心内泰勒气泡变得更加扁平，修长。靠近弯曲壁面的两个流道分支内的气相体积明显减少，大量气泡在另一边的流道分支内聚集。泰勒气泡在经过弯曲段后逐渐变厚，但整体偏向弯曲壁面的对角面一侧并与之有大面积的接触。随着闭合度的不断增加，弯曲段内泰勒气泡间的距离也逐渐增大。

4.3 棒弯曲对局部空泡分布的影响

（1） 入口含气率 = 0.1

如图6 棒弯曲最大截面处两相分布云图，流道中心的气泡形状随着闭合度的不断增加，整体形状逐渐扁平化。当一根棒束与另外两个完全接触时，流道严重压缩变形，流道中心的气泡出现与弯曲壁面接触的情况，即弯曲棒束壁面出现裸露，此时该处的传热将急剧恶化，严重时可能导致CHF 的提前发生。50%闭合度子通道中心气泡下部存在极为突兀的凹陷，如图7 所示，在该处凹陷附近可以观察到一个较大的二次流涡流，涡流的旋向与凹陷极为匹配，这种情况在80%闭合度模型的其它截面中也能观察到。

（2） 入口含气率为0.5

如图8 所示为入口含气率0.5 时流道中心存在体积较大的泰勒气泡，其易与四个圆弧壁面发生接触。直棒通道内，气弹可能与任意壁面发生接触，从而使壁面出现裸露情况，而在较高弯曲程度时则主要与弯曲壁面或其对角面相接触，即CHF 更有可能发生在这两个壁面。在泰勒气泡的气芯内夹杂着一些小液滴，液滴夹带现象更易在壁面弯曲时的子通道内被观察到。在子通道的一些部位，截面平均空泡份额大大高于0.5，此时该界面呈现在高含气率时出现的液相堆积在四个流道分支内，中心流道被气相完全占据的情况，这种情况在完全接触模型中极为普遍。在50%闭合度子通道模型中观察到靠近弯曲壁面对角面一侧的两相界面发生向内的凹陷。如图9 所示，弯曲面对侧两流道分支内形成了两个较强的二次流涡流，在其影响下，两相界面产生了较为明显的畸变。

5 结论

本文采用VOF 摸型对棒弯曲子通道内两相流动进行了数值研究。主要工作和结论如下：

（1） 壁面弯曲对截面平均空泡份额的影响较小，但在中部截面闭合度大的子通道面积较小，即空泡的体积也相对较小。

（2） 弯曲壁面会使流道中心气泡形状趋于扁平化，同时也会使其位置向曲面对角侧偏移，液相更容易在弯曲壁面流道分支内聚集。在较大闭合度的子通道中弯曲壁面及其对角面容易发生裸露，CHF 更有可能发生在该处。

（3） 两相界面及不规则流道促使了二次流涡流的形成，而二次流涡流的形成又改变了局部空泡的分布情况，导致空泡形状的畸变。