三维电阻抗层析成像的跨层激励研究

张宇展 钟航宇 梁 坤 桑子豪 孙犇渊

中国民航大学中欧航空工程师学院 天津 300300

电阻抗层析成像技术(Electrical Impedance Tomography，简称EIT)起源于20世纪20年代，它的基本原理是根据在不同情况下材料具有不同的电阻/电导率，采用各种方法对被测物体施加驱动电流/电压，通过测量被测场域周围的响应信息，从而重建其内部电导率分布的图像。

目前的建模和图像重建的大部分研究都是围绕二维电阻抗层析成像展开的，然而，实际应用中，获取三维上的分布信息可以更直观地感知场域的电学特性的分布情况。体积图像对于工业应用也至关重要，例如，流速剖面和体积分数测量。

3D-EIT在传感器设计、激励测量策略、有限元模拟、算法构建等方面还有待进一步深入研究。2019年，Rafiul K.Rasel等人研究并量化了简化跨平面采集策略对优化图像重建和抑制电学成像病态性的影响。本文在此基础上，进一步探究三维电阻抗层析成像中跨层激励对图像重建的影响。

1 EIT的数学模型

设

u

为求解域的电势分布，

σ

为求解域的电导率分布，则EIT的数学模型可以由麦克斯韦方程组及似稳场假设推出：

(1)

其中，

I

为从第

l

个电极

E

注入的电流，

E

具有接触阻抗

z

。

V

是电极

E

上的电压，

n

是向外的单位法向量。电阻抗层析成像的正问题是已知电导率分布及边界注入电流情况，求解边界电极的测量电压。线性化方法是基于电场灵敏度理论的线性求解方法。由于求解域的边界电压信息

U

唯一的由场域的电导率分布

σ

确定，即:

U

=

F

(

σ

)

(2)

可以考虑将求解域分割为

N

个体元，计算每个体元电导率发生微小变化时边界电压的变化，即可获得该求解域的灵敏度场信息。则可写为：

ΔU

=

JΔσ

(3)

其中，

ΔU

为

M

×1维的矩阵，包含了在不同激励模式下电极对的电压值变化；

Δσ

为

N

×1维的矩阵，为电导率变化量；

J

为

M

×

N

维的灵敏度矩阵或Jacobian矩阵。

借助David B.Geselowitz于1971年提出的四端口网络的阻抗灵敏度表达式，可以大大减少求解灵敏度矩阵所花费的时间。

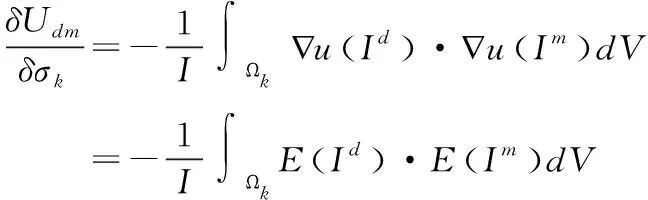
(4)

其中，Ω为第

k

个体元，

u

(

I

)和

u

(

I

)分别为第

d

个电极对和第

m

个电极对被激励且激励电流为

I

时的电势分布，

E

(

I

)和

E

(

I

)分别为第

d

个电极对和第

m

个电极对被激励且激励电流为

I

时的电场分布。

为简化逆问题的求解，方程可归一化为：

z

=

Sg

(5)

式中，

z

为

N

×1维的测量值矩阵，

S

为

M

×

N

维的归一化灵敏度矩阵，

g

为

M

×1维的灰度值矩阵。

2 仿真模型建立

2.1 正问题模型

本文在有限元仿真软件COMSOL Multiphysics 3.5a上建立EIT系统模型并进行仿真计算获取有关参数。EIT模型设计了七层16电极模型，如图1所示。

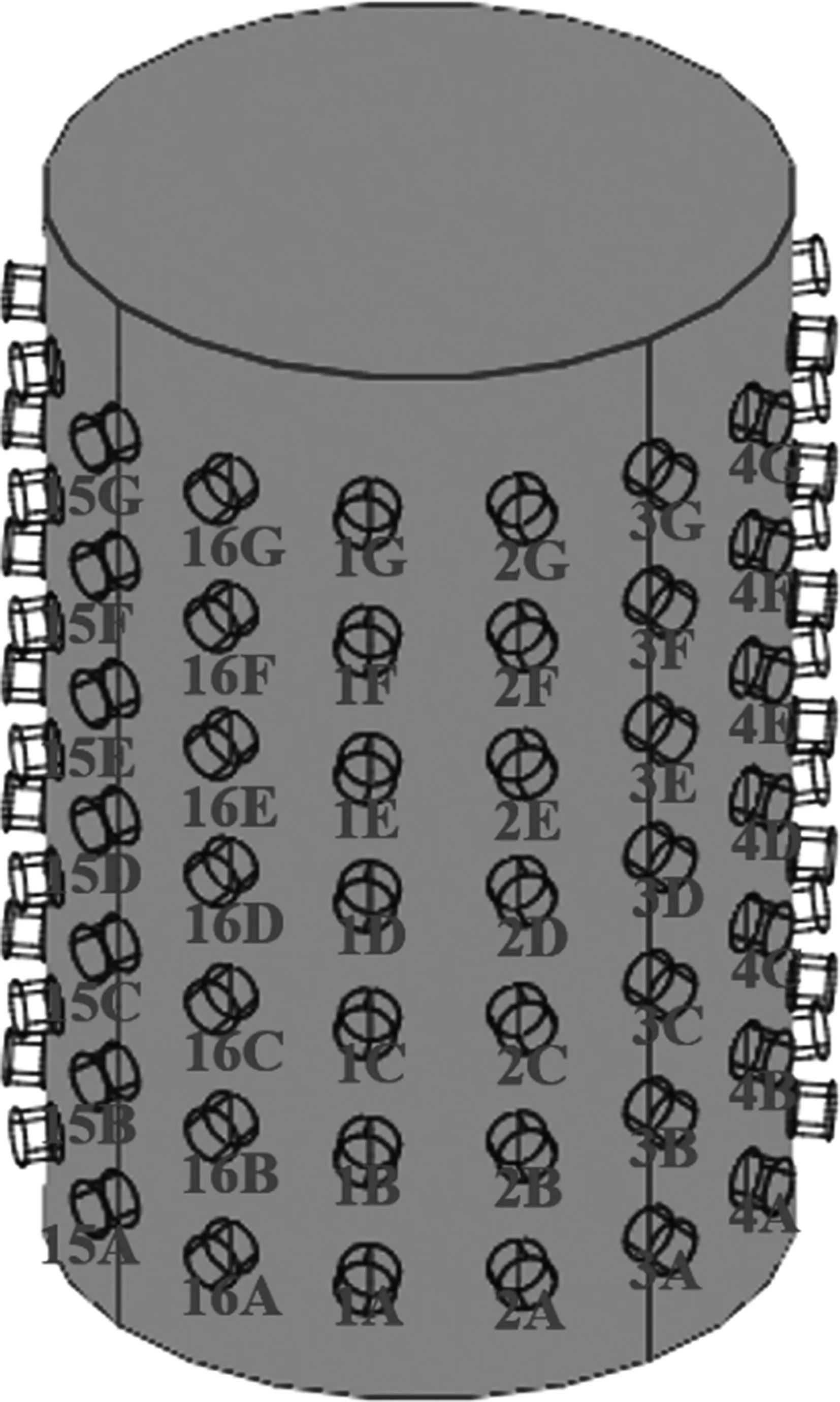
(a)物理模型

(b)有限元模型图1 七层16电极EIT模型

圆柱形容器的半径为20cm，高度为62.8cm，内部是电导率为1S/m。电极形状为圆柱形，电导率设置为钛的电导率7.407×10S/m，排布方式上采用了陈晓艳等人提出的占空比为0.4的方案。依照此方案，电极的半径设置为1.57cm，高度为2cm，分别位于高度为7.85cm、15.70cm、23.55cm、31.40cm、39.25cm、47.10cm、54.95cm的七个平面上。

2.2 激励测量模式

为讨论跨层激励对图像重建的影响，本文采取的激励测量模式主要分为两类，分别为同层相邻驱动的策略以及跨层方形驱动的策略。

同层相邻驱动的策略类似于2D-EIT的相邻激励相邻测量模式，电流由相邻电极注入，同时按激励顺序测量除激励电极之外的各相邻电极之间的电压差，如图2所示。电极的激励顺序为：1A—2A—3A—…15A—16A，具体激励测量方案为：激励1A和2A电极，测量(3A—4A)(4A—5A)……(15A—16A)电极间的电压，然后激励2A和3A电极，测量(4A—5A)(5A—6A)……(16A—1A)电极间的电压，直到所有电极对都被激励过。

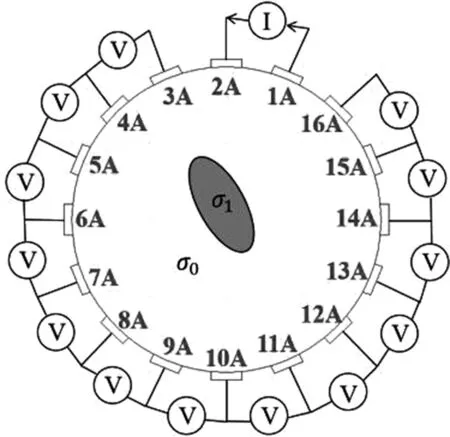
图2 同层驱动模式

跨层方形驱动的策略将平面的相邻驱动的延伸到了三维上，以中间层(D层)上下各跨一层为例，电极的激励顺序为：1D—1E—2E—2D—2C—3C—3D—…—16D—16C—1C；电极测量方式类似同层相邻驱动的策略，按激励顺序测量除激励电极之外的各相邻电极之间的电压差。

我们将七层各层仅采取同层驱动时来获得3D EIT直接成像数据的设置称为

E

0。对应的，对于跨层驱动策略，

En

指的是中间层(D层)及中间层上下

n

层数量的跨平面驱动的设置。例如，

E

2指的是在B、C、D、E、F五层间采取跨层驱动策略时的采集。

2.3 逆问题模型

图3展示了本文设置的两种分布情况，成像目标的电导率均设置为3S/m。

(a)

(b)图3 两种分布的位置情况

圆柱体目标和球体目标的半径为4cm，图3(a)中左侧球的球心距离底面36.65cm，右侧球的球心到底面的距离分别为10.47cm、20.94cm、31.42cm、41.89cm、52.36cm；图3(b)中左侧球的球心到底面的距离分别为19.42cm、31.42cm、43.42cm。

3 实验结果

下表展示了两种分布在不同激励方案下的使用共轭梯度迭代法求解逆问题然后直接3D成像的结果，重建物是取最大值的0.5倍的等值面绘成的。

不同分布的图像重建结果表

对比不同激励层数的直接3D成像，随着激励层数的增加，获取的3D信息也就越全面，对原始分布的还原越精确。对比分布一在不同激励模式下成像结果，可以明显发现，

E

0的“粘连”现象比较严重，已经无法区分五个球体，而

E

3的可以明显区别五个球体。对于分布二，

E

0对于圆柱体的还原比较好，而

E

3对于物体的间隔显示更清楚。结合分析可知，跨层激励与同层激励相比，跨层激励获取了

z

轴方向上的信息，在

z

轴方向上还原更准确，而没有像同层激励一样由于缺乏立体信息而出现“粘连”现象。相反的，也正是因为这样，同层激励对

z

轴方向上连续变化的物体(如圆柱形物体)的还原比跨层激励的要更准确。

结语

经过上述的仿真以及结果分析可以得知，对于EIT直接3D成像，跨层激励的数量将影响

z

轴方向上信息的提取，跨的层数越多，对图像的还原越准确，对EIT系统也会提出更高的要求。通过对多种分布的对比，同层激励的方案对于电导率在

z

轴方向上连续变化的物体的重建效果更好，但总体上，跨层驱动可以更好地还原原始的分布情况。